Perturbación (astronomía)

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Enfoque clásico del problema de muchos cuerpos de la astronomía

En astronomía, perturbación es el movimiento complejo de un cuerpo masivo sometido a fuerzas distintas a la atracción gravitacional de otro cuerpo masivo. Las otras fuerzas pueden incluir un tercer cuerpo (cuarto, quinto, etc.), la resistencia, como la de una atmósfera, y la atracción descentrada de un cuerpo achatado o deforme.

Introducción

El estudio de las perturbaciones comenzó con los primeros intentos de predecir los movimientos planetarios en el cielo. En la antigüedad se desconocían las causas. Isaac Newton, al tiempo que formuló sus leyes del movimiento y de la gravitación, las aplicó al primer análisis de las perturbaciones, reconociendo las complejas dificultades de su cálculo. Desde entonces, muchos de los grandes matemáticos han prestado atención a los diversos problemas involucrados; A lo largo de los siglos XVIII y XIX hubo demanda de tablas precisas de la posición de la Luna y los planetas para la navegación marítima.

Los movimientos complejos de las perturbaciones gravitacionales se pueden descomponer. El movimiento hipotético que sigue el cuerpo bajo el efecto gravitacional de otro cuerpo únicamente es una sección cónica y puede describirse en términos geométricos. Esto se denomina problema de dos cuerpos o órbita kepleriana no perturbada. Las diferencias entre éste y el movimiento real del cuerpo son perturbaciones debidas a los efectos gravitacionales adicionales del cuerpo o cuerpos restantes. Si sólo hay otro cuerpo significativo, entonces el movimiento perturbado es un problema de tres cuerpos; si hay muchos otros cuerpos, es un problema de n cuerpos. Existe una solución analítica general (una expresión matemática para predecir las posiciones y movimientos en cualquier momento futuro) para el problema de los dos cuerpos; cuando se consideran más de dos cuerpos, las soluciones analíticas existen sólo para casos especiales. Incluso el problema de los dos cuerpos se vuelve insoluble si uno de los cuerpos tiene una forma irregular.

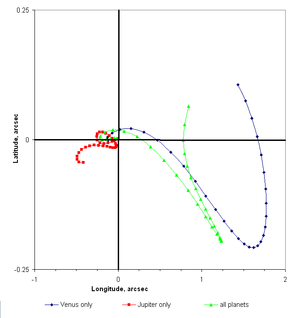
La mayoría de los sistemas que involucran múltiples atracciones gravitacionales presentan un cuerpo primario que es dominante en sus efectos (por ejemplo, una estrella, en el caso de la estrella y su planeta, o un planeta, en el caso del planeta y su satélite). ). Los efectos gravitacionales de los otros cuerpos pueden tratarse como perturbaciones del hipotético movimiento no perturbado del planeta o satélite alrededor de su cuerpo primario.

Análisis matemático

Perturbaciones generales

En los métodos de perturbaciones generales, las ecuaciones diferenciales generales, ya sea de movimiento o de cambio en los elementos orbitales, se resuelven analíticamente, generalmente mediante expansiones en serie. El resultado suele expresarse en términos de funciones algebraicas y trigonométricas de los elementos orbitales del cuerpo en cuestión y de los cuerpos perturbadores. Esto se puede aplicar en general a muchos conjuntos diferentes de condiciones y no es específico de ningún conjunto particular de objetos gravitantes. Históricamente, primero se investigaron las perturbaciones generales. Los métodos clásicos se conocen como variación de los elementos, variación de parámetros o variación de las constantes de integración. En estos métodos, se considera que el cuerpo siempre se mueve en una sección cónica, sin embargo, la sección cónica cambia constantemente debido a las perturbaciones. Si todas las perturbaciones cesaran en un instante determinado, el cuerpo continuaría en esta sección cónica (ahora inmutable) indefinidamente; esta cónica se conoce como órbita osculadora y sus elementos orbitales en un momento determinado son los que se buscan mediante los métodos de perturbaciones generales.

Perturbaciones generales aprovecha el hecho de que en muchos problemas de mecánica celeste, la órbita de dos cuerpos cambia bastante lentamente debido a las perturbaciones; la órbita de dos cuerpos es una buena primera aproximación. Las perturbaciones generales son aplicables sólo si las fuerzas perturbadoras son aproximadamente un orden de magnitud más pequeñas, o menos, que la fuerza gravitacional del cuerpo primario. En el Sistema Solar, este suele ser el caso; Júpiter, el segundo cuerpo más grande, tiene una masa de aproximadamente 1/1000 la del Sol.

Se prefieren los métodos de perturbación general para algunos tipos de problemas, ya que la fuente de ciertos movimientos observados se encuentra fácilmente. Esto no es necesariamente así para perturbaciones especiales; los movimientos se predecirían con similar precisión, pero no se dispondría de información sobre las configuraciones de los cuerpos perturbadores (por ejemplo, una resonancia orbital) que los provocaron.

Perturbaciones especiales

En los métodos de perturbaciones especiales, los conjuntos de datos numéricos, que representan valores para las posiciones, velocidades y fuerzas de aceleración en los cuerpos de interés, se convierten en la base de la integración numérica de las ecuaciones diferenciales de movimiento. En efecto, las posiciones y velocidades se perturban directamente y no se intenta calcular las curvas de las órbitas ni de los elementos orbitales.

Se pueden aplicar perturbaciones especiales a cualquier problema de mecánica celeste, ya que no se limita a casos en los que las fuerzas perturbadoras son pequeñas. Los métodos de perturbación especiales, que antes se aplicaban sólo a cometas y planetas menores, son ahora la base de las efemérides planetarias generadas por máquinas más precisas de los grandes almanaques astronómicos. También se utilizan perturbaciones especiales para modelar una órbita con computadoras.

Formulación de Cowell

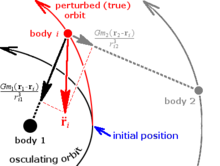
La formulación de Cowell (también llamada por Philip H. Cowell, quien, con A.C.D. Cromellin, usó un método similar para predecir el regreso del cometa de Halley) es quizás el más simple de los métodos especiales de perturbación. En un sistema de ${displaystyle n }$ cuerpos que interactúan mutuamente, este método resuelve matemáticamente para las fuerzas Newtonianas en el cuerpo ${displaystyle i }$ resumiendo las interacciones individuales del otro ${displaystyle j}$ cuerpos:

{displaystyle mathbf {ddot {r}} _{i}=sum _{underset {jneq i}{j=1}}^{n} G m_{j}{frac { (mathbf {r} _{j}-mathbf {r} _{i}) }{ |mathbf {r} _{j}-mathbf {r} _{i}|^{3}}}}

Donde ${displaystyle mathbf {ddot {r}} _{i} }$ es el vector de aceleración del cuerpo ${displaystyle i}$ , ${displaystyle G}$ es la constante gravitacional, ${displaystyle m_{j} }$ es la masa del cuerpo ${displaystyle j}$ , ${displaystyle mathbf {r} _{i} }$ y ${displaystyle mathbf {r} _{j} }$ son los vectores de posición de los objetos ${displaystyle i }$ y ${displaystyle j }$ respectivamente ${displaystyle r_{ij}equiv |mathbf {r} _{j}-mathbf {r} _{i}| }$ es la distancia del objeto ${displaystyle i}$ a objeto ${displaystyle j }$ , todos los vectores se refieren al barycenter del sistema. Esta ecuación se resuelve en componentes ${displaystyle x}$ ${displaystyle y}$ y ${displaystyle z}$ y estos son integrados numéricamente para formar la nueva velocidad y los vectores de posición. Este proceso se repite tantas veces como sea necesario. La ventaja del método de Cowell es la facilidad de aplicación y programación. Una desventaja es que cuando las perturbaciones se vuelven grandes en magnitud (como cuando un objeto hace un acercamiento cercano a otro) los errores del método también se vuelven grandes. Sin embargo, para muchos problemas en la mecánica celestial, este nunca es el caso. Otra desventaja es que en sistemas con un cuerpo central dominante, como el Sol, es necesario llevar muchos dígitos significativos en la aritmética debido a la gran diferencia en las fuerzas del cuerpo central y los cuerpos perturbadores, aunque con números de alta precisión construidos en computadoras modernas esto no es tanto de una limitación como una vez fue.

Método de Encke

El método de Encke comienza con la órbita osculante como referencia y la integra numéricamente para resolver la variación desde la referencia en función del tiempo. Sus ventajas son que las perturbaciones son generalmente de magnitud pequeña, por lo que la integración puede realizarse en pasos más grandes (con menores errores resultantes), y el método se ve mucho menos afectado por perturbaciones extremas. Su desventaja es la complejidad; no se puede utilizar indefinidamente sin actualizar ocasionalmente la órbita osculadora y continuar desde allí, proceso conocido como rectificación. El método de Encke es similar al método de perturbación general de variación de los elementos, excepto que la rectificación se realiza a intervalos discretos en lugar de continuamente.

Letting ${displaystyle {boldsymbol {rho }}}$ ser el vector radial de la órbita osculante, ${displaystyle mathbf {r} }$ el vector radial de la órbita perturbia, y ${displaystyle delta mathbf {r} }$ la variación de la órbita osculante,

{displaystyle delta mathbf {r} =mathbf {r} -{boldsymbol {rho }}}

, y la ecuación del movimiento

{displaystyle delta mathbf {r} }

es simplemente

()1)

{displaystyle {ddot {delta mathbf {r} }}=mathbf {ddot {r}} -{boldsymbol {ddot {rho }}}}

()2)

${displaystyle mathbf {ddot {r}} }$ y ${displaystyle {boldsymbol {ddot {rho }}}}$ son sólo las ecuaciones de movimiento de ${displaystyle mathbf {r} }$ y ${displaystyle {boldsymbol {rho }},}$

{displaystyle mathbf {ddot {r}} =mathbf {a} _{text{per}}-{mu over r^{3}}mathbf {r} }

para la órbita perturbida

()3)

{displaystyle {boldsymbol {ddot {rho }}}=-{mu over rho ^{3}}{boldsymbol {rho }}}

para la órbita no perturbada,

()4)

Donde ${displaystyle mu =G(M+m)}$ es el parámetro gravitacional con ${displaystyle M}$ y ${displaystyle m}$ las masas del cuerpo central y el cuerpo perturbado, ${displaystyle mathbf {a} _{text{per}}}$ es la aceleración inquietante, y ${displaystyle r}$ y ${displaystyle rho }$ son las magnitudes de ${displaystyle mathbf {r} }$ y ${displaystyle {boldsymbol {rho }}}$ .

Sustitución de ecuaciones ()3) y (4) en la ecuación (2),

{displaystyle {ddot {delta mathbf {r} }}=mathbf {a} _{text{per}}+mu left({{boldsymbol {rho }} over rho ^{3}}-{mathbf {r} over r^{3}}right),}

()5)

que, en teoría, podría integrarse dos veces para encontrar ${displaystyle delta mathbf {r} }$ . Puesto que la órbita osculante se calcula fácilmente mediante métodos de dos cuerpos, ${displaystyle {boldsymbol {rho }}}$ y ${displaystyle delta mathbf {r} }$ se contabilizan y ${displaystyle mathbf {r} }$ puede ser resuelto. En la práctica, la cantidad entre corchetes, ${displaystyle {{boldsymbol {rho }} over rho ^{3}}-{mathbf {r} over r^{3}}}$ , es la diferencia de dos vectores casi iguales, y es necesaria una mayor manipulación para evitar la necesidad de dígitos extra significativos. El método de Encke fue más utilizado antes del advenimiento de computadoras modernas, cuando se realizó mucha computación de órbita sobre máquinas de cálculo mecánica.

Naturaleza periódica

En el Sistema Solar, muchas de las perturbaciones de un planeta por otro son periódicas, consistentes en pequeños impulsos cada vez que un planeta pasa por otro en su órbita. Esto hace que los cuerpos sigan movimientos que son periódicos o cuasi-peródicos, como la Luna en su órbita fuertemente perturbada, que es el tema de la teoría lunar. Esta naturaleza periódica llevó al descubrimiento de Neptuno en 1846 como resultado de sus perturbaciones de la órbita de Urano.

Las perturbaciones mutuas en curso de los planetas provocan variaciones cuasi-peródicas a largo plazo en sus elementos orbitales, más evidentes cuando los períodos orbitales de dos planetas están casi sincronizados. Por ejemplo, cinco órbitas de Júpiter (59,31 años) son casi iguales a dos de Saturno (58,91 años). Esto causa grandes perturbaciones de ambos, con un período de 918 años, el tiempo necesario para la pequeña diferencia en sus posiciones en conjunto para hacer un círculo completo, primero descubierto por Laplace. Venus tiene actualmente la órbita con la menor excentricidad, es decir, es la más cercana a la circular, de todas las órbitas planetarias. En 25.000 años, la Tierra tendrá una órbita más circular (menos excéntrica) que Venus. Se ha demostrado que las perturbaciones periódicas a largo plazo dentro del Sistema Solar pueden convertirse en caóticas a largo plazo; bajo algunas circunstancias uno o más planetas pueden cruzar la órbita de otro, dando lugar a colisiones.

Las órbitas de muchos de los cuerpos menores del Sistema Solar, como los cometas, a menudo están fuertemente perturbadas, especialmente por los campos gravitatorios de los gigantes del gas. Aunque muchas de estas perturbaciones son periódicas, otras no lo son, y éstas en particular pueden representar aspectos del movimiento caótico. Por ejemplo, en abril de 1996, la influencia gravitatoria de Júpiter causó que el período de la órbita de Comet Hale-Bopp disminuyera de 4.206 a 2.380 años, un cambio que no revertirá sobre ninguna base periódica.

Contenido relacionado

Más resultados...