Perceptrón

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Algoritmo para el aprendizaje supervisado de clasificadores binarios

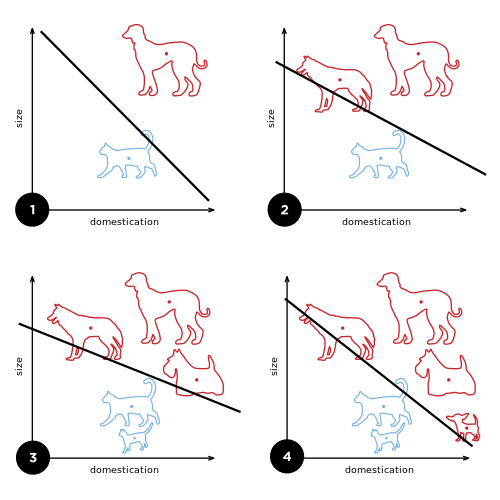
En el aprendizaje automático, el perceptrón (o neurona de McCulloch-Pitts) es un algoritmo para el aprendizaje supervisado de clasificadores binarios. Un clasificador binario es una función que puede decidir si una entrada, representada por un vector de números, pertenece o no a una clase específica. Es un tipo de clasificador lineal, es decir, un algoritmo de clasificación que hace sus predicciones basándose en una función predictora lineal que combina un conjunto de pesos con el vector de características.

Historia

Mark I Perceptron machine, la primera implementación del algoritmo de perceptron. Fue conectado a una cámara con fotocélulas de sulfuro de cadmio 20×20 para hacer una imagen de 400 píxeles. La característica visible principal es un panel de parche que establece diferentes combinaciones de características de entrada. A la derecha, arrays de potenciómetros que implementaban los pesos adaptativos.

El perceptrón fue inventado en 1943 por Warren McCulloch y Walter Pitts. La primera implementación fue una máquina construida en 1958 en el Laboratorio Aeronáutico de Cornell por Frank Rosenblatt, financiada por la Oficina de Investigación Naval de los Estados Unidos.

Sistema de cámara de la marca 1 Perceptron.

El perceptrón estaba destinado a ser una máquina, en lugar de un programa, y aunque su primera implementación fue en software para IBM 704, posteriormente se implementó en hardware personalizado como el "perceptrón Mark 1". Esta máquina fue diseñada para el reconocimiento de imágenes: tenía una matriz de 400 fotocélulas, conectadas aleatoriamente a las 'neuronas'. Los pesos se codificaron en potenciómetros y las actualizaciones de peso durante el aprendizaje se realizaron mediante motores eléctricos.

En una conferencia de prensa de 1958 organizada por la Marina de los EE. UU., Rosenblatt hizo declaraciones sobre el perceptrón que provocaron una acalorada controversia entre la incipiente comunidad de IA; basado en las declaraciones de Rosenblatt, The New York Times informó que el perceptrón es "el embrión de una computadora electrónica que [la Marina] espera que sea capaz de caminar, hablar, ver, escribir, reproducirse y ser consciente de su existencia."

Aunque inicialmente el perceptrón parecía prometedor, rápidamente se demostró que los perceptrones no podían entrenarse para reconocer muchas clases de patrones. Esto provocó que el campo de la investigación de redes neuronales se estancara durante muchos años, antes de que se reconociera que una red neuronal feedforward con dos o más capas (también llamada perceptrón multicapa) tenía mayor poder de procesamiento que los perceptrones con una capa (también llamada red de una sola capa). perceptrón de capa).

Los perceptrones de una sola capa solo son capaces de aprender patrones linealmente separables. Para una tarea de clasificación con alguna función de activación de pasos, un solo nodo tendrá una sola línea que divide los puntos de datos que forman los patrones. Más nodos pueden crear más líneas divisorias, pero esas líneas deben combinarse de alguna manera para formar clasificaciones más complejas. Una segunda capa de perceptrones, o incluso nodos lineales, es suficiente para resolver muchos problemas que de otro modo no serían separables.

En 1969, un famoso libro titulado Perceptrons de Marvin Minsky y Seymour Papert demostró que era imposible que estas clases de redes aprendieran una función XOR. A menudo se cree (incorrectamente) que también conjeturaron que un resultado similar se mantendría para una red de perceptrones multicapa. Sin embargo, esto no es cierto, ya que tanto Minsky como Papert ya sabían que los perceptrones multicapa eran capaces de producir una función XOR. (Consulte la página sobre Perceptrones (libro) para obtener más información). Sin embargo, el texto de Minsky/Papert, a menudo mal citado, provocó una disminución significativa en el interés y la financiación de la investigación de redes neuronales. Pasaron diez años más hasta que la investigación de redes neuronales experimentó un resurgimiento en la década de 1980. Este texto se reimprimió en 1987 como "Perceptrones - Edición ampliada" donde se muestran y corrigen algunos errores en el texto original.

Un artículo de 2022 afirma que el Mark 1 Perceptron era "parte de un NPIC de cuatro años previamente secreto [los EE. UU.' Centro Nacional de Interpretación Fotográfica] desde 1963 hasta 1966 para convertir este algoritmo en una herramienta útil para los fotointérpretes.

El algoritmo kernel perceptron ya fue introducido en 1964 por Aizerman et al. Freund y Schapire (1998), y más recientemente Mohri y Rostamizadeh (2013), quienes extendieron los resultados anteriores y dieron nuevos límites L1, dieron garantías de límites de margen para el algoritmo Perceptron en el caso general no separable.

El perceptrón es un modelo simplificado de una neurona biológica. Si bien a menudo se requiere la complejidad de los modelos de neuronas biológicas para comprender completamente el comportamiento neuronal, la investigación sugiere que un modelo lineal similar a un perceptrón puede producir algunos comportamientos que se ven en las neuronas reales.

Definición

En el sentido moderno, el perceptron es un algoritmo para aprender un clasificador binario llamado función umbral: una función que mapea su entrada $mathbf {x}$ (un vector de valor real) a un valor de salida $f(mathbf {x})$ (un único valor binario):

0,\0&{text{otherwise}}end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">f()x)={}1siw⋅ ⋅ x+b■0,0de otra manera{displaystyle f(mathbf {x})={begin{cases}1 {text{if}mathbf {w}cdot mathbf {x} - ¿Por qué?0,\0&{text{otherwise}}end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c27b30e07934b4fc8f346ec6fafd5b077d0d4efc" style="vertical-align: -2.505ex; width:29.864ex; height:6.176ex;"/>

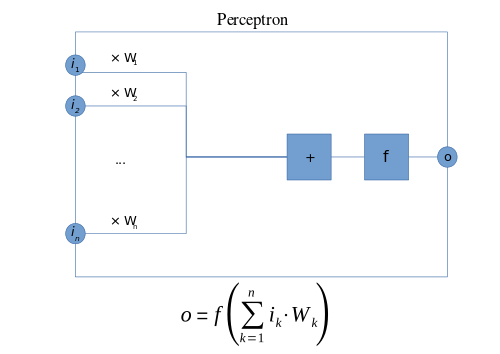
Donde $mathbf {w}$ es un vector de pesos reales, ${displaystyle mathbf {w} cdot mathbf {x} }$ es el producto de punto ${displaystyle sum _{i=1}^{m}w_{i}x_{i}}$ , donde $m$ es el número de entradas al perceptrón, y $b$ es parciales. El sesgo desplaza el límite de decisión lejos del origen y no depende de ningún valor de entrada.

El valor de $f(mathbf {x})$ (0 o 1) se utiliza para clasificar $mathbf {x}$ como una instancia positiva o negativa, en el caso de un problema de clasificación binaria. Si $b$ es negativo, entonces la combinación ponderada de insumos debe producir un valor positivo mayor que $|b|$ para empujar la neurona clasificatoria sobre el umbral 0. Espacialmente, el sesgo altera la posición (aunque no la orientación) del límite de decisión. El algoritmo de aprendizaje de perceptron no termina si el conjunto de aprendizaje no es linealmente separable. Si los vectores no son un aprendizaje linealmente separable nunca llegará a un punto donde todos los vectores se clasifican correctamente. El ejemplo más famoso de la incapacidad del perceptrón para resolver problemas con vectores linealmente no estables es el problema exclusivo o exclusivo booleano. Los espacios de solución de límites de decisión para todas las funciones binarias y comportamientos de aprendizaje son estudiados en la referencia.

En el contexto de las redes neuronales, un perceptrón es una neurona artificial que utiliza la función de paso de Heaviside como función de activación. El algoritmo del perceptrón también se denomina perceptrón de una sola capa, para distinguirlo de un perceptrón multicapa, que es un nombre inapropiado para una red neuronal más complicada. Como clasificador lineal, el perceptrón de una sola capa es la red neuronal de avance más simple.

Algoritmo de aprendizaje

A continuación se muestra un ejemplo de un algoritmo de aprendizaje para un perceptrón de una sola capa. Para los perceptrones multicapa, donde existe una capa oculta, se deben usar algoritmos más sofisticados, como la retropropagación. Si la función de activación o el proceso subyacente que modela el perceptrón no es lineal, se pueden utilizar algoritmos de aprendizaje alternativos, como la regla delta, siempre que la función de activación sea diferenciable. No obstante, el algoritmo de aprendizaje descrito en los pasos a continuación funcionará a menudo, incluso para perceptrones multicapa con funciones de activación no lineales.

Cuando se combinan varios perceptrones en una red neuronal artificial, cada neurona de salida funciona independientemente de las demás; por lo tanto, el aprendizaje de cada salida se puede considerar de forma aislada.

Definiciones

Primero definimos algunas variables:

r es la tasa de aprendizaje del perceptrón. La tasa de aprendizaje es entre 0 y 1. Los valores más grandes hacen que los cambios de peso sean más volátiles.
${displaystyle y=f(mathbf {z})}$ denota los Producto del perceptron para un vector de entrada $mathbf {z}$ .
D={}()x1,d1),...... ,()xs,ds)}{displaystyle D={(mathbf {x} _{1},d_{1}),dots(mathbf {x} _{s},d_{s})}} ${displaystyle D={(mathbf {x} _{1},d_{1}),dots(mathbf {x} _{s},d_{s})}}$ es Conjunto de capacitación de s{displaystyle s} $s$ muestras, donde:
- $mathbf {x} _{j}$ es $n$ - vector de entrada dimensional.
- ${displaystyle d_{j}}$ es el valor de salida deseado del perceptrón para esa entrada.

Mostramos los valores de las características de la siguiente manera:

${displaystyle x_{j,i}}$ es el valor del $i$ t característica de la $j$ capacitación vector.
${displaystyle x_{j,0}=1}$ .

Para representar los pesos:

${displaystyle w_{i}}$ es $i$ valor en el vector de peso, para ser multiplicado por el valor del $i$ función de entrada.
Porque... ${displaystyle x_{j,0}=1}$ , el ${displaystyle w_{0}}$ es efectivamente un sesgo que usamos en lugar de la constante del sesgo $b$ .

Para mostrar el tiempo-dependencia de $mathbf {w}$ , usamos:

${displaystyle w_{i}(t)}$ es el peso $i$ a la vez $t$ .

Pasos

Inicia los pesos. Los pesos pueden ser inicializados a 0 o a un pequeño valor aleatorio. En el ejemplo a continuación, utilizamos 0.
Para cada ejemplo j en nuestro set de entrenamiento D, realizar los siguientes pasos sobre la entrada xj{displaystyle mathbf {x} _{j} ${mathbf {x}}_{j}$ y la salida deseada dj{displaystyle D_{j} ${displaystyle d_{j}}$ :
1. Calcular la salida real:
  ${displaystyle {begin{aligned}y_{j}(t)&=f[mathbf {w} (t)cdot mathbf {x} _{j}]\&=f[w_{0}(t)x_{j,0}+w_{1}(t)x_{j,1}+w_{2}(t)x_{j,2}+dotsb +w_{n}(t)x_{j,n}]end{aligned}}}$
2. Actualizar los pesos:
  ${displaystyle w_{i}(t+1)=w_{i}(t);{boldsymbol {+}};rcdot (d_{j}-y_{j}(t))x_{j,i}}$ , para todas las características $0leq ileq n$ , $r$ es la tasa de aprendizaje.
Para el aprendizaje offline, el segundo paso puede repetirse hasta el error de iteración ${displaystyle {frac {1}{s}}sum _{j=1}^{s}|d_{j}-y_{j}(t)|}$ es menos que un umbral de error especificado por el usuario $gamma$ , o un número predeterminado de iteraciones se han completado, donde s es de nuevo el tamaño del conjunto de la muestra.

El algoritmo actualiza los pesos después de los pasos 2a y 2b. Estos pesos se aplican inmediatamente a un par en el conjunto de entrenamiento y luego se actualizan, en lugar de esperar hasta que todos los pares en el conjunto de entrenamiento hayan realizado estos pasos.

Un diagrama que muestra un perceptron actualizando su límite lineal mientras se añaden más ejemplos de entrenamiento

Los pesos apropiados se aplican a las entradas, y la suma ponderada resultante pasa a una función que produce la salida o.

Convergencia

El perceptrón es un clasificador lineal, por lo que nunca llegará al estado con todos los vectores de entrada clasificados correctamente si el conjunto de entrenamiento $D$ no es linealmente separable, es decir, si los ejemplos positivos no pueden separarse de los ejemplos negativos por un hiperplano. En este caso, no hay "aproximado" La solución se abordará gradualmente bajo el algoritmo de aprendizaje estándar, pero en cambio, el aprendizaje fallará por completo. Por lo tanto, si no se conoce a priori la separabilidad lineal del conjunto de entrenamiento, se debe usar una de las variantes de entrenamiento a continuación.

Si el conjunto de entrenamiento es linealmente separable, entonces se garantiza que el perceptrón convergerá. Además, existe un límite superior en el número de veces que el perceptrón ajustará sus pesos durante el entrenamiento.

Supongamos que los vectores de entrada de las dos clases pueden ser separados por un hiperplano con un margen $gamma$ , es decir, existe un vector de peso $mathbf {w}||mathbf {w} ||=1$ , y un término de sesgo $b$ tales que $gamma }" xmlns="http://www.w3.org/1998/Math/MathML">w⋅ ⋅ xj■γ γ {displaystyle mathbf {w} cdot mathbf {x} _{j}gamma }gamma }" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/4ac2c20ebc8cb445c80afb46b93539f72f0d5ec1" style="vertical-align: -1.005ex; width:10.292ex; height:2.509ex;"/>$ para todos $j$ con ${displaystyle d_{j}=1}$ y $<math alttext="{displaystyle mathbf {w} cdot mathbf {x} _{j}w⋅ ⋅ xj.− − γ γ {displaystyle mathbf {w} cdot mathbf {x} _{j} made-gamma }<img alt="{displaystyle mathbf {w} cdot mathbf {x} _{j}$ para todos $j$ con ${displaystyle d_{j}=0}$ , donde $d_{j}$ es el valor de salida deseado del perceptrón para la entrada $j$ . Además, deja $R$ denota la norma máxima de un vector de entrada. Novikoff (1962) demostró que en este caso el algoritmo de perceptron converge después de hacer $O(R^{2}/gamma ^{2})$ actualizaciones. La idea de la prueba es que el vector de peso siempre se ajusta por una cantidad atada en una dirección con la que tiene un producto de punto negativo, y por lo tanto puede ser atado arriba por $O () \sqrt t)$ , donde $t$ es el número de cambios en el vector de peso. Sin embargo, también puede ser atado a continuación por $O () t)$ porque si existe un (no conocido) vector de peso satisfactorio, entonces cada cambio hace progresos en esta dirección (no conocida) por una cantidad positiva que depende sólo del vector de entrada.

Dos clases de puntos, y dos de los infinitamente muchos límites lineales que los separan. Aunque los límites están en ángulos casi rectos entre sí, el algoritmo de perceptron no tiene forma de elegir entre ellos.

Si bien se garantiza que el algoritmo del perceptrón convergerá en alguna solución en el caso de un conjunto de entrenamiento linealmente separable, aún puede elegir cualquier solución y los problemas pueden admitir muchas soluciones de calidad variable. El perceptrón de estabilidad óptima, hoy más conocido como máquina lineal de vectores soporte, fue diseñado para resolver este problema (Krauth y Mezard, 1987).

Variantes

El algoritmo de bolsillo con trinquete (Gallant, 1990) resuelve el problema de estabilidad del aprendizaje del perceptrón manteniendo la mejor solución vista hasta ahora 'en su bolsillo'. El algoritmo de bolsillo luego devuelve la solución en el bolsillo, en lugar de la última solución. También se puede usar para conjuntos de datos no separables, donde el objetivo es encontrar un perceptrón con una pequeña cantidad de clasificaciones erróneas. Sin embargo, estas soluciones aparecen de forma puramente estocástica y, por lo tanto, el algoritmo de bolsillo no se acerca a ellas gradualmente en el curso del aprendizaje, ni se garantiza que aparezcan dentro de un número determinado de pasos de aprendizaje.

El algoritmo de Maxover (Wendemuth, 1995) es "robusto" en el sentido de que convergerá independientemente del conocimiento (previo) de la separabilidad lineal del conjunto de datos. En el caso de separación lineal, resolverá el problema de entrenamiento, si se desea, incluso con una estabilidad óptima (margen máximo entre las clases). Para conjuntos de datos no separables, devolverá una solución con una pequeña cantidad de clasificaciones erróneas. En todos los casos, el algoritmo se acerca gradualmente a la solución en el curso del aprendizaje, sin memorizar estados previos y sin saltos estocásticos. La convergencia es a la optimización global para conjuntos de datos separables y a la optimización local para conjuntos de datos no separables.

El perceptrón votado (Freund y Schapire, 1999) es una variante que utiliza múltiples perceptrones ponderados. El algoritmo inicia un nuevo perceptrón cada vez que un ejemplo está mal clasificado, inicializando el vector de pesos con los pesos finales del último perceptrón. A cada perceptrón también se le dará otro peso correspondiente a cuántos ejemplos clasifican correctamente antes de clasificar uno incorrectamente, y al final el resultado será un voto ponderado en todos los perceptrones.

En problemas separables, el entrenamiento del perceptrón también puede apuntar a encontrar el mayor margen de separación entre las clases. El llamado perceptrón de estabilidad óptima puede determinarse mediante esquemas iterativos de entrenamiento y optimización, como el algoritmo Min-Over (Krauth y Mezard, 1987) o el AdaTron (Anlauf y Biehl, 1989)). AdaTron utiliza el hecho de que el problema de optimización cuadrático correspondiente es convexo. El perceptrón de estabilidad óptima, junto con el truco del kernel, son los fundamentos conceptuales de la máquina de vectores soporte.

El $alpha$ -perceptron utilizó además una capa de procesamiento previo de pesos fijos aleatorios, con unidades de salida umbral. Esto permitió al perceptrón clasificar patrones analógicos, proyectandolos en un espacio binario. De hecho, para un espacio de proyección de dimensión suficientemente alta, los patrones pueden ser linealmente separables.

Otra forma de resolver problemas no lineales sin utilizar varias capas es utilizar redes de orden superior (unidad sigma-pi). En este tipo de red, cada elemento en el vector de entrada se extiende con cada combinación por pares de entradas multiplicadas (segundo orden). Esto se puede extender a una red de orden n.

Debe tenerse en cuenta, sin embargo, que el mejor clasificador no es necesariamente el que clasifica perfectamente todos los datos de entrenamiento. De hecho, si tuviéramos la restricción previa de que los datos provienen de distribuciones gaussianas equivariantes, la separación lineal en el espacio de entrada es óptima y la solución no lineal está sobreajustada.

Otros algoritmos de clasificación lineal incluyen Winnow, máquina de vectores de soporte y regresión logística.

Perceptrón multiclase

Al igual que la mayoría de otras técnicas para la formación de clasificadores lineales, el perceptron generaliza naturalmente a la clasificación multiclase. Aquí, la entrada $x$ y la producción $y$ son extraídos de conjuntos arbitrarios. Una función de representación característica $f(x,y)$ mapas cada posible par de entrada/salida a un vector de característica de valor real finito. Como antes, el vector de características se multiplica por un vector de peso $w$ , pero ahora la puntuación resultante se utiliza para elegir entre muchas salidas posibles:

{hat {y}}=operatorname {argmax} _{y}f(x,y)cdot w.

Volver a aprender itera sobre los ejemplos, prediciendo una salida para cada uno, dejando los pesos sin cambios cuando la salida pronosticada coincide con el objetivo y cambiándolos cuando no lo hace. La actualización se convierte en:

w_{t+1}=w_{t}+f(x,y)-f(x,{hat {y}}).

Esta formulación de retroalimentación multiclase reduce al perceptrón original cuando $x$ es un vector de valor real, $y$ es elegido ${0,1}$ , y $f(x,y)=yx$ .

Para ciertos problemas, se pueden elegir representaciones y características de entrada/salida para que $mathrm {argmax} _{y}f(x,y)cdot w$ se puede encontrar eficientemente aunque $y$ es elegido de un conjunto muy grande o incluso infinito.

Desde 2002, el entrenamiento con perceptrones se ha vuelto popular en el campo del procesamiento del lenguaje natural para tareas como el etiquetado de partes del discurso y el análisis sintáctico (Collins, 2002). También se ha aplicado a problemas de aprendizaje automático a gran escala en un entorno informático distribuido.

Contenido relacionado

Más resultados...