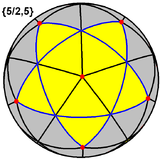
Pequeño dodecaedro estrellado
| Pequeño dodecaedro estelar | |
|---|---|
 | |
| Tipo | Kepler-Poinsot polihedron |
| núcleo de la estelación | regular dodecahedron |
| Elementos | F = 12, E = 30 V = 12 (χ = -6) |
| Caras por lados | 12 5 |
| Símbolo Schläfli | {}5.2,5} |
| Configuración facial | V(5)5)/2 |
| Signatura Wythoff | 5 latitud 2 5.2 |
| Coxeter diagrama |      |
| Grupo de simetría | Ih, H3[5,3], (*532) |
| Referencias | U34C43W20 |
| Propiedades | Regular nonconvex |
 ()5.2)5 (Vertex figure) |  Gran dodecahedron (poliedro dual) |
En geometría, el pequeño dodecaedro estrellado es un poliedro de Kepler-Poinsot, nombrado así por Arthur Cayley, y con el símbolo de Schläfli { 5⁄2,5}. Es uno de los cuatro poliedros regulares no convexos. Está compuesto por 12 caras pentagramáticas, con cinco pentagramas reunidos en cada vértice.
Comparte la misma disposición de vértices que el icosaedro regular convexo. También comparte la misma disposición de bordes con el gran icosaedro, con el que forma una figura compuesta uniforme degenerada.
Es la segunda de cuatro estelaciones del dodecaedro (incluido el dodecaedro original).
El pequeño dodecaedro estrellado se puede construir de manera análoga al pentagrama, su análogo bidimensional, mediante la extensión de los bordes (caras 1) del politopo central hasta alcanzar un punto donde se cruzan.
Topología
Si las caras pentagramáticas se consideran 5 caras triangulares, comparten la misma topología de superficie que el dodecaedro pentakis, pero con caras de triángulos isósceles mucho más altas, con la altura de las pirámides pentagonales ajustada para que los cinco triángulos del pentagrama se conviertan en coplanar. El ángulo crítico es atan(2) por encima de la cara del dodecaedro.
Si consideramos que tiene 12 pentagramas como caras, con estos pentagramas conectándose en 30 aristas y 12 vértices, podemos calcular su género usando la fórmula de Euler.
- V− − E+F=2− − 2g{displaystyle V-E+F=2-2g}
y concluir que el pequeño dodecaedro estelar tiene género 4. Esta observación, realizada por Louis Poinsot, fue inicialmente confusa, pero Felix Klein mostró en 1877 que el pequeño dodecaedro estelar podía verse como una cubierta ramificada de la esfera Riemann por una superficie Riemann del género 4, con puntos de rama en el centro de cada pentagrama. De hecho esta superficie Riemann, llamada Trae la curva, tiene el mayor número de simetrías de cualquier superficie Riemann del género 4: el grupo simétrico S5{displaystyle S_{5} actúa como automorfismos
Imágenes
| Modelo transparente | Modelos hechos a mano | |
|---|---|---|
 (Ver también: animado) |  |  |
| Tilo esférico | Stellation | Net |
 Este poliedro también representa un revestimiento esférico con una densidad de 3. (Una cara esférica de pentagrama, delineada en azul, llena de amarillo) |  También se puede construir como la primera de tres estelas del dodecaedro, y referencia como modelo Wenninger [W20]. |  × 12La pequeña dodecahedra estelar se puede construir a partir de papel o cartón, conectando juntos 12 pirámides isosceles de cinco lados de la misma manera que los pentágonos en un dodecaedro regular. Con un material opaco, esto representa visualmente la porción exterior de cada cara pentagrama. |
En el arte
Un pequeño dodecaedro estelar se puede ver en un mosaico de suelo en la basílica de San Marcos, Venecia por Paolo Uccello c.1430. La misma forma es central en dos litografías de M. C. Escher: Contraste (Order and Chaos) (1950) y Gravitación (1952).
Fórmulas
Para un pequeño dodecaedro estrellado con una longitud de arista E,
- Circumradius = E4()50+225){fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}} {f}}} {fnMicrosoft}}} {fn}}}}}}} {\fnMicroc}} {f}}}} {f}}}}}} {f}}}}}}} { Bigl (}{sqrt {50+22{sqrt {5}} {Bigr)}}}
- Superficie = 15()5+25)E2{displaystyle 15{Bigl (}{sqrt {5+2{sqrt {5}} {Bigr)}E^{2}}
- Volumen = 54()7+35)E3{displaystyle {tfrac {5}{4}}(7+3{sqrt E^{3}
Poliedros relacionados
Su casco convexo es el icosaedro convexo regular. También comparte sus aristas con el gran icosaedro; el compuesto con ambos es el gran complejo icosidodecaedro.
Hay cuatro poliedros uniformes relacionados, construidos como grados de truncamiento. El dual es un gran dodecaedro. El dodecadodecaedro es una rectificación, donde las aristas se truncan hasta formar puntos.
El dodecaedro estrellado pequeño truncado puede considerarse un poliedro uniforme degenerado ya que las aristas y los vértices coinciden, pero se incluye para completarlo. Visualmente, parece un dodecaedro regular en la superficie, pero tiene 24 caras en pares superpuestos. Las púas se truncan hasta alcanzar el plano del pentagrama debajo de ellas. Las 24 caras son 12 pentágonos de los vértices truncados y 12 decágonos que toman la forma de pentágonos doblemente enrollados que se superponen a los primeros 12 pentágonos. Estas últimas caras se forman truncando los pentagramas originales. Cuando un {n⁄d}-gon se trunca, se convierte en un {2n⁄d}-gon. Por ejemplo, un pentágono truncado {5⁄1} se convierte en un decágono. {10⁄1}, por lo que truncar un pentagrama {5⁄2} se convierte en un pentágono doblemente enrollado {10⁄2} (el factor común entre 10 y 2 significa que visitamos cada vértice dos veces para completar el polígono).
| Estabilizaciones del dodecaedro | ||||||
| sólido platónico | sólidos Kepler-Poinsot | |||||
| Dodecahedron | Pequeño dodecaedro estelar | Gran dodecahedron | Gran dodecaedro estelar | |||
|---|---|---|---|---|---|---|
 |  |  |  | |||
 | |  |  | |||
| Nombre | Pequeño dodecaedro estelar | Truncado pequeño dodecaedro estelar | Dodecadodecahedron | Truncatedgreatdodecahedron | Greatdodecahedron |
|---|---|---|---|---|---|
| Coxeter-Dynkindiagram | | | | | |
| Imagen | |  |  |  | |