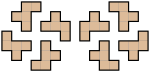
Pentomino

Los 12 pentominos pueden formar 18 formas diferentes, con 6 de ellas (los pentominos chiral) siendo reflejados.

Derivado de la palabra griega para '5', y "domino", un pentomino (o 5-omino) es un poliominó de orden 5, es decir, un polígono en el plano formado por 5 cuadrados del mismo tamaño conectados de arista con arista. Cuando las rotaciones y los reflejos no se consideran formas distintas, hay 12 pentominós libres diferentes. Cuando los reflejos se consideran distintos, hay 18 pentominós de un solo lado. Cuando las rotaciones también se consideran distintas, hay 63 pentominós fijos.

Los rompecabezas y juegos de mosaicos de Pentomino son populares en las matemáticas recreativas. Por lo general, los videojuegos como las imitaciones de Tetris y Rampart consideran que los reflejos del espejo son distintos y, por lo tanto, utilizan el conjunto completo de 18 pentominós de una cara.

Cada uno de los doce pentominós satisface el criterio de Conway; por lo tanto, cada pentominó es capaz de embaldosar el plano. Cada pentomino quiral puede teselar el plano sin ser reflejado.

Historia

Comparación de esquemas de etiquetado para las 12 posibles formas pentomino. La primera convención de nombres es la utilizada en este artículo. El segundo método es el de Conway.

El primer rompecabezas que contenía un juego completo de pentóminos apareció en el libro de Henry Dudeney, Los rompecabezas de Canterbury, publicado en 1907. Las primeras teselaciones de rectángulos con un juego completo de pentóminos aparecieron en Problemist Fairy Chess Supplement en 1935., y se exploraron más problemas de mosaico en PRCS y su sucesor, Fairy Chess Review. Los pentominós fueron definidos formalmente por el profesor estadounidense Solomon W. Golomb a partir de 1953 y más tarde en su libro de 1965 Polyominoes: Puzzles, Patterns, Problems, and Packings. Fueron presentados al público en general por Martin Gardner en su columna de juegos matemáticos de octubre de 1965 en Scientific American. Golomb acuñó el término "pentomino" del griego antiguo πέντε / pénte, "cinco", y el -omino de dominó, interpretando fantasiosamente la "d-" de "dominó" como si fuera una forma del prefijo griego "di-" (dos). Golomb nombró los 12 pentominós libres según las letras del alfabeto latino a las que se parecen.

John Horton Conway propuso un esquema de etiquetado alternativo para los pentominós, utilizando O en lugar de I, Q en lugar de L, R en lugar de F y S en lugar de N. El parecido con las letras es más tenso, especialmente para el pentominó O., pero este esquema tiene la ventaja de usar 12 letras consecutivas del alfabeto. Se usa por convención al discutir el Juego de la vida de Conway, donde, por ejemplo, se habla del R-pentomino en lugar del F-pentomino.

Simetría

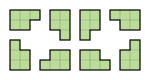
• F, L, N, P y Y se pueden orientar en 8 formas: 4 por rotación, y 4 más para la imagen del espejo. Su grupo de simetría consiste sólo en el mapeo de identidad.
• T, y U pueden orientarse en 4 formas por rotación. Tienen un eje de reflexión alineado con las redes. Su grupo de simetría tiene dos elementos, la identidad y la reflexión en una línea paralela a los lados de los cuadrados.
• V y W también pueden orientarse en 4 formas por rotación. Tienen un eje de simetría de reflexión a 45° a las redes. Su grupo de simetría tiene dos elementos, la identidad y una reflexión diagonal.
• Z se puede orientar de 4 maneras: 2 por rotación, y 2 más para la imagen del espejo. Tiene simetría de puntos, también conocida como simetría rotacional del orden 2. Su grupo de simetría tiene dos elementos, la identidad y la rotación de 180°.
• Puedo orientarme de dos maneras por rotación. Tiene dos ejes de simetría de reflexión, ambos alineados con las redes. Su grupo de simetría tiene cuatro elementos, la identidad, dos reflexiones y la rotación de 180°. Es el grupo dihedral de orden 2, también conocido como el grupo Klein cuatro.
• X se puede orientar de una sola manera. Tiene cuatro ejes de simetría de reflexión, alineados con las rejillas y las diagonales, y simetría rotacional del orden 4. Su grupo de simetría, el grupo dihedral del orden 4, tiene ocho elementos.

Los pentominós F, L, N, P, Y y Z son quirales; sumando sus reflejos (F′, J, N′, Q, Y′, S) eleva el número de pentominós de un solo lado a 18. Si las rotaciones también se consideran distintas, entonces los pentominós del primer la categoría cuenta ocho veces, las de las siguientes tres categorías (T, U, V, W, Z) cuentan cuatro veces, I cuenta dos veces y X cuenta solo una vez. Esto da como resultado 5×8 + 5×4 + 2 + 1 = 63 pentominós fijos.

Por ejemplo, las ocho orientaciones posibles de los pentominós L, F, N, P e Y son las siguientes:

Para las figuras 2D en general, hay dos categorías más:

• Ser orientable de 2 maneras por una rotación de 90°, con dos ejes de simetría de reflexión, ambos alineados con las diagonales. Este tipo de simetría requiere al menos un heptomino.
• Ser orientable de 2 maneras, que son las imágenes del espejo del otro, por ejemplo una esvástica. Este tipo de simetría requiere al menos un octomino.

Construcción de dimensiones rectangulares

Un rompecabezas de pentominós estándar consiste en teselar una caja rectangular con los pentominós, es decir, cubrirla sin solapamientos ni espacios. Cada uno de los 12 pentominós tiene un área de 5 cuadrados unitarios, por lo que la caja debe tener un área de 60 unidades. Los tamaños posibles son 6×10, 5×12, 4×15 y 3×20.

El caso 6×10 fue resuelto por primera vez en 1960 por Colin Brian Haselgrove y Jenifer Haselgrove. Hay exactamente 2339 soluciones, excluyendo variaciones triviales obtenidas por rotación y reflexión de todo el rectángulo, pero incluyendo rotación y reflexión de un subconjunto de pentominós (lo que a veces proporciona una solución adicional de forma sencilla). La caja de 5×12 tiene 1010 soluciones, la caja de 4×15 tiene 368 soluciones y la caja de 3×20 tiene solo 2 soluciones (una se muestra en la figura y la otra se puede obtener de la solución que se muestra rotando, como un todo, el bloque que consta de los pentominós L, N, F, T, W, Y y Z).

Un rompecabezas un poco más fácil (más simétrico), el rectángulo de 8×8 con un agujero de 2×2 en el centro, fue resuelto por Dana Scott ya en 1958. Hay 65 soluciones. El algoritmo de Scott fue una de las primeras aplicaciones de un programa informático de retroceso. Las variaciones de este rompecabezas permiten colocar los cuatro agujeros en cualquier posición. Uno de los enlaces externos utiliza esta regla. La mayoría de estos patrones se pueden resolver, con la excepción de colocar cada par de agujeros cerca de dos esquinas del tablero de tal manera que ambas esquinas solo puedan encajar con un P-pentomino, o forzar un T-pentomino o U-pentomino en un esquina tal que se crea otro agujero.

Se han descrito algoritmos eficientes para resolver este tipo de problemas, por ejemplo, por Donald Knuth. Al ejecutarse en hardware moderno, estos acertijos pentomino ahora se pueden resolver en cuestión de segundos.

El conjunto pentomino es el único conjunto poliominó libre que se puede empaquetar en un rectángulo, con la excepción de los conjuntos triviales monomino y dominó, cada uno de los cuales consta de un solo rectángulo.

Llenado de cajas

Un pentacubo es un policubo de cinco cubos. De los 29 pentacubos, exactamente doce pentacubos son planos (una capa) y corresponden a los doce pentominós extruidos a una profundidad de un cuadrado.

A pentacube puzzle o 3D pentomino puzzle, equivale a llenar una caja tridimensional con los 12 pentacubos planos, es decir, cubrirlo sin solapamiento y sin huecos. Puesto que cada pentacube tiene un volumen de 5 cubos de unidad, la caja debe tener un volumen de 60 unidades. Los tamaños posibles son 2×3×10 (12 soluciones), 2×5×6 (264 soluciones) y 3×4×5 (3940 soluciones). Seguir es una solución de cada caso.

Alternativamente, también se podrían considerar combinaciones de cinco cubos que son en sí mismos 3D, es decir, que no forman parte de una capa de cubos. Sin embargo, además de los 12 pentominós extruidos, 6 conjuntos de pares quirales y 5 piezas hacen un total de 29 piezas, lo que da como resultado 145 cubos, que no formarán una caja 3D (ya que 145 solo puede ser 29 × 5 × 1, que el no -los pentominós planos no pueden caber).

Juegos de mesa

Hay juegos de mesa de habilidad basados enteramente en pentominós. Estos juegos a menudo se denominan simplemente "Pentominoes".

Uno de los juegos se juega en una cuadrícula de 8×8 por dos o tres jugadores. Los jugadores se turnan para colocar pentominós en el tablero para que no se superpongan con las fichas existentes y ninguna ficha se use más de una vez. El objetivo es ser el último jugador en colocar una ficha en el tablero. Esta versión de Pentominoes se llama "Golomb's Game".

La versión de dos jugadores fue débilmente resuelta en 1996 por Hilarie Orman. Se demostró que era una victoria para el primer jugador al examinar alrededor de 22 mil millones de posiciones en el tablero.

Los pentominós y formas similares también son la base de una serie de otros juegos, patrones y rompecabezas. Por ejemplo, el juego de mesa francés Blokus se juega con 4 juegos de poliominós de colores, cada uno de los cuales consta de cada pentominó (12), tetrominó (5), triominó (2), dominó (1) y monominó (1).). Al igual que el juego Pentominoes, el objetivo es utilizar todas las fichas y se otorga una bonificación si se juega el monomino en el último movimiento. El jugador con la menor cantidad de bloques restantes gana.

El juego de Cathedral también se basa en poliominós.

Parker Brothers lanzó un juego de mesa pentomino multijugador llamado Universe en 1966. Su tema se basa en una escena eliminada de la película de 1968 2001: A Space Odyssey en en el que un astronauta está jugando un juego de pentominó de dos jugadores contra la computadora HAL 9000 (se retuvo una escena con un astronauta diferente jugando al ajedrez). El frente de la caja del juego de mesa presenta escenas de la película, así como una leyenda que lo describe como el "juego del futuro". El juego viene con cuatro juegos de pentominós en rojo, amarillo, azul y blanco. El tablero tiene dos áreas jugables: un área base de 10x10 para dos jugadores con 25 cuadrados adicionales (dos filas más de 10 y una fila compensada de cinco) en cada lado para más de dos jugadores.

El fabricante de juegos Lonpos tiene varios juegos que usan los mismos pentominós, pero en diferentes planos de juego. Su Juego 101 tiene un plano de 5 x 11. Al cambiar la forma del avión, se pueden jugar miles de rompecabezas, aunque solo una selección relativamente pequeña de estos rompecabezas está disponible impresa.

Literatura

Los pentominós aparecieron en una trama secundaria destacada de la novela Imperial Earth de Arthur C. Clarke de 1975. Clarke también escribió un ensayo en el que describía el juego y cómo se enganchó a él.

También aparecieron en Chasing Vermeer de Blue Balliett, que se publicó en 2003 e ilustrado por Brett Helquist, así como en sus secuelas, The Wright 3 y El juego de Calder.

En el crucigrama del New York Times del 27 de junio de 2012, la pista para una palabra de 11 letras de 37 de ancho era "Conjunto completo de 12 formas formadas por los cuadrados negros de este crucigrama&#39.' 34;

Videojuegos

• Tetris se inspiró en rompecabezas pentomino, aunque utiliza tetrominos de cuatro bloques. Algunos clones y variantes Tetris, como el juego 5s incluido con el Plan 9 de Bell Labs, y Magical Tetris ChallengeUsa pentominos.
• Daedalian Opus utiliza rompecabezas pentomino a lo largo del juego.