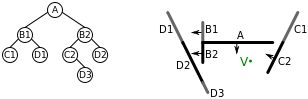Partición de espacio binario

El proceso de hacer un árbol BSP

En informática, la partición de espacio binario (BSP) es un método de partición de espacio que subdivide de forma recursiva un espacio euclidiano en dos conjuntos convexos mediante el uso de hiperplanos como particiones. Este proceso de subdivisión da lugar a una representación de objetos dentro del espacio en forma de una estructura de datos de árbol conocida como árbol BSP.

La partición del espacio binario se desarrolló en el contexto de los gráficos 3D por computadora en 1969. La estructura de un árbol BSP es útil en la representación porque puede brindar información espacial de manera eficiente sobre los objetos en una escena, como los objetos que se ordenan desde el frente. espalda con respecto a un espectador en un lugar dado. Otras aplicaciones de BSP incluyen: realizar operaciones geométricas con formas (geometría sólida constructiva) en CAD, detección de colisiones en robótica y videojuegos 3D, trazado de rayos y otras aplicaciones que involucran el manejo de escenas espaciales complejas.

Resumen

La partición de espacio binario es un proceso genérico de dividir recursivamente una escena en dos hasta que la partición satisfaga uno o más requisitos. Puede verse como una generalización de otras estructuras de árboles espaciales, como los árboles k-d y los árboles cuádruples, uno en el que los hiperplanos que dividen el espacio pueden tener cualquier orientación, en lugar de estar alineados con los ejes de coordenadas como están en k-d árboles o quadtrees. Cuando se utiliza en gráficos por computadora para renderizar escenas compuestas por polígonos planos, los planos de partición se eligen con frecuencia para que coincidan con los planos definidos por los polígonos en la escena.

La elección específica del plano de partición y el criterio para finalizar el proceso de partición varía según el propósito del árbol BSP. Por ejemplo, en la representación de gráficos por computadora, la escena se divide hasta que cada nodo del árbol BSP contiene solo polígonos que se pueden representar en un orden arbitrario. Cuando se utiliza la selección de cara posterior, cada nodo, por lo tanto, contiene un conjunto convexo de polígonos, mientras que cuando se representan polígonos de dos lados, cada nodo del árbol BSP contiene solo polígonos en un solo plano. En la detección de colisiones o el trazado de rayos, una escena se puede dividir en primitivas en las que las pruebas de colisión o intersección de rayos son sencillas.

La partición del espacio binario surgió de la necesidad de gráficos por computadora para dibujar rápidamente escenas tridimensionales compuestas de polígonos. Una forma sencilla de dibujar este tipo de escenas es el algoritmo del pintor, que produce polígonos en orden de distancia desde el espectador, de atrás hacia adelante, pintando sobre el fondo y los polígonos anteriores con cada objeto más cercano. Este enfoque tiene dos desventajas: el tiempo necesario para ordenar los polígonos de atrás hacia adelante y la posibilidad de errores en los polígonos superpuestos. Fuchs y sus coautores demostraron que la construcción de un árbol BSP resolvía ambos problemas al proporcionar un método rápido para ordenar los polígonos con respecto a un punto de vista dado (lineal en el número de polígonos en la escena) y al subdividir los polígonos superpuestos para evitar errores que puede ocurrir con el algoritmo del pintor. Una desventaja de la partición del espacio binario es que generar un árbol BSP puede llevar mucho tiempo. Normalmente, por lo tanto, se realiza una vez en geometría estática, como un paso de cálculo previo, antes del renderizado u otras operaciones en tiempo real en una escena. El costo de construir un árbol BSP hace que sea difícil e ineficiente implementar directamente objetos en movimiento en un árbol.

Los árboles BSP se utilizan a menudo en videojuegos 3D, en particular en los juegos de disparos en primera persona y en aquellos con ambientes interiores. Los motores de juego que utilizan árboles BSP incluyen los motores Doom (id Tech 1), Quake (variante id Tech 2), GoldSrc y Source. En ellos, los árboles BSP que contienen la geometría estática de una escena a menudo se usan junto con un búfer Z para fusionar correctamente objetos móviles como puertas y personajes en la escena de fondo. Si bien la partición del espacio binario proporciona una forma conveniente de almacenar y recuperar información espacial sobre los polígonos en una escena, no resuelve el problema de la determinación de la superficie visible.

Generación

El uso canónico de un árbol BSP es para renderizar polígonos (que son de doble cara, es decir, sin eliminar la cara posterior) con el algoritmo del pintor. Cada polígono se designa con un anverso y un reverso que pueden elegirse arbitrariamente y solo afectan la estructura del árbol pero no el resultado requerido. Dicho árbol se construye a partir de una lista desordenada de todos los polígonos de una escena. El algoritmo recursivo para la construcción de un árbol BSP a partir de esa lista de polígonos es:

1. Elija un polígono P de la lista.
2. Hacer un nodo N en el árbol BSP, y añadir P a la lista de polígonos en ese nodo.
3. Para el otro polígono en la lista:
   1. Si ese polígono está totalmente delante del plano que contiene P, mover ese polígono a la lista de nodos delante de P.
   2. Si ese polígono está completamente detrás del plano que contiene P, mover ese polígono a la lista de nodos detrás P.
   3. Si ese polígono está intersectado por el plano que contiene P, dividirlo en dos polígonos y moverlos a las respectivas listas de polígonos detrás y delante de P.
   4. Si ese polígono se encuentra en el plano que contiene P, añadirlo a la lista de polígonos en nodo N.
4. Aplica este algoritmo a la lista de polígonos delante de P.
5. Aplicar este algoritmo a la lista de polígonos detrás P.

El siguiente diagrama ilustra el uso de este algoritmo para convertir una lista de líneas o polígonos en un árbol BSP. En cada uno de los ocho pasos (i.-viii.), el algoritmo anterior se aplica a una lista de líneas y se agrega un nuevo nodo al árbol.

	Comience con una lista de líneas, (o en 3D, polígonos) formando la escena. En los diagramas de árboles, las listas son denotadas por rectángulos redondeados y nodos en el árbol BSP por círculos. En el diagrama espacial de las líneas, la dirección elegida para ser la "frontera" de una línea se denota por una flecha.
i.	Siguiendo los pasos del algoritmo anterior, Escogemos una línea, A, de la lista y... ... se lo dio a un nodo. Dividimos las líneas restantes de la lista en las que están delante de A (es decir, B2, C2, D2), y las que están detrás (B1, C1, D1). Primero procesamos las líneas delante de A (en pasos ii-v),... ...seguida por aquellos detrás (en pasos vi-vii).
ii.	Ahora aplicamos el algoritmo a la lista de líneas delante de A (contiene B2, C2, D2). Elegimos una línea, B2, añadirla a un nodo y dividir el resto de la lista en aquellas líneas que están delante de B2 (D2), y las que están detrás de ella (C2, D3).
iii.	Elige una línea, D2, de la lista de líneas delante de B2 y A. Es la única línea de la lista, así que después de añadirla a un nodo, nada más debe hacerse.
iv.	Hemos terminado con las líneas delante de B2, así que considere las líneas detrás de B2 (C2 y D3). Elija uno de estos (C2), agréguelo a un nodo, y ponga la otra línea en la lista (D3) en la lista de líneas delante de C2.
v.	Ahora mira la lista de líneas delante de C2. Sólo hay una línea (D3), por lo que añadir esto a un nodo y continuar.
vi.	Ahora hemos añadido todas las líneas delante de A al árbol BSP, así que ahora empezamos en la lista de líneas detrás de A. Elegir una línea (B1) de esta lista, agregamos B1 a un nodo y dividimos el resto de la lista en líneas delante de B1 (es decir, D1), y líneas detrás de B1 (es decir, C1).
vii.	Procesar primero la lista de líneas delante de B1, D1 es la única línea en esta lista, por lo que añadir esto a un nodo y continuar.
viii.	Mirando al lado de la lista de líneas detrás de B1, la única línea en esta lista es C1, así que agrega esto a un nodo, y el árbol BSP está completo.

La cantidad final de polígonos o líneas en un árbol suele ser mayor (a veces mucho mayor) que la lista original, ya que las líneas o polígonos que cruzan el plano de partición deben dividirse en dos. Es deseable minimizar este aumento, pero también mantener un equilibrio razonable en el árbol final. Por lo tanto, la elección de qué polígono o línea se utiliza como plano de partición (en el paso 1 del algoritmo) es importante para crear un árbol BSP eficiente.

Transversal

Un árbol BSP se recorre en un tiempo lineal, en un orden determinado por la función particular del árbol. Nuevamente, usando el ejemplo de renderizar polígonos de dos lados usando el algoritmo del pintor, para dibujar un polígono P correctamente se requiere que todos los polígonos detrás del plano P se encuentren en dibujarse primero, luego el polígono P, luego finalmente los polígonos delante de P. Si este orden de dibujo se cumple para todos los polígonos de una escena, la escena completa se renderiza en el orden correcto. Este procedimiento se puede implementar atravesando recursivamente un árbol BSP usando el siguiente algoritmo. Desde una ubicación de visualización determinada V, para representar un árbol BSP,

1. Si el nodo actual es un nodo de hoja, render los polígonos en el nodo actual.
2. De lo contrario, si el lugar de visualización V está delante del nodo actual:
   1. Render al niño árbol BSP que contiene polígonos detrás del nodo actual
   2. Render los polígonos en el nodo actual
   3. Render el niño árbol BSP que contiene polígonos delante del nodo actual
3. De lo contrario, si el lugar de visualización V está detrás del nodo actual:
   1. Render el niño árbol BSP que contiene polígonos delante del nodo actual
   2. Render los polígonos en el nodo actual
   3. Render al niño árbol BSP que contiene polígonos detrás del nodo actual
4. De lo contrario, la ubicación de visualización V debe estar exactamente en el avión asociado con el nodo actual. Entonces:
   1. Render el niño árbol BSP que contiene polígonos delante del nodo actual
   2. Render al niño árbol BSP que contiene polígonos detrás del nodo actual

Aplicar este algoritmo recursivamente al árbol BSP generado anteriormente da como resultado los siguientes pasos:

• El algoritmo se aplica primero al nodo raíz del árbol, nodo A. V está delante del nodo A, por lo que aplicamos el algoritmo primero al niño árbol BSP que contiene polígonos detrás A
  • Este árbol tiene nudo raíz B1. V está detrás B1 así que primero aplicamos el algoritmo al niño árbol BSP que contiene polígonos delante de B1:
    • Este árbol es sólo el nodo de hoja D1, así que el polígono D1 está hecho.
  • Luego hacemos el polígono B1.
  • A continuación aplicamos el algoritmo al niño árbol BSP que contiene polígonos detrás B1:
    • Este árbol es sólo el nodo de hoja C1, así que el polígono C1 está hecho.
• Luego dibujamos los polígonos de A
• Luego aplicamos el algoritmo al niño árbol BSP que contiene polígonos delante de A
  • Este árbol tiene nudo raíz B2. V está detrás B2 así que primero aplicamos el algoritmo al niño árbol BSP que contiene polígonos delante de B2:
    • Este árbol es sólo el nodo de hoja D2, así que el polígono D2 está hecho.
  • Luego hacemos el polígono B2.
  • A continuación aplicamos el algoritmo al niño árbol BSP que contiene polígonos detrás B2:
    • Este árbol tiene nudo raíz C2. V está delante C2 así que primero aplicaríamos el algoritmo al niño árbol BSP que contiene polígonos detrás C2. No hay tal árbol, sin embargo, así que continuamos.
    • Presentamos el polígono C2.
    • Aplicamos el algoritmo al niño árbol BSP que contiene polígonos delante de C2
      • Este árbol es sólo el nodo de hoja D3, así que el polígono D3 está hecho.

El árbol se recorre en tiempo lineal y representa los polígonos en un orden de lejos a cerca (D1, B1, C1, A, D2, B2, C2, D3) adecuado para el pintor&# 39;s algoritmo.

Cronología

• 1969 Schumacker et al. publicaron un informe que describió cómo los planos cuidadosamente posicionados en un entorno virtual podrían ser utilizados para acelerar el pedido de polígonos. La técnica hizo uso de la coherencia de profundidad, que afirma que un polígono en el lado lejano del plano no puede, de ninguna manera, obstruir un polígono más cercano. Esto fue utilizado en simuladores de vuelo realizados por GE, así como Evans y Sutherland. Sin embargo, la creación de la organización de datos poligonales fue realizada manualmente por el diseñador de escena.

• 1980 Fuchs et al. Extendió la idea de Schumacker a la representación de objetos 3D en un entorno virtual utilizando planos que coinciden con polígonos para dividir el espacio 3D recursivamente. Esto proporcionó una generación totalmente automatizada y algorítmica de una estructura jerárquica de datos poligonales conocida como Árbol de Partición del Espacio binario (Árbol BSP). El proceso tuvo lugar como un paso de preprocesamiento fuera de línea que se realizó una vez por medio ambiente/objeto. A la hora de correr, el orden de visibilidad dependiente de la vista se generó atravesando el árbol.
• 1981 La tesis doctoral de Naylor proporcionó un desarrollo completo de los árboles BSP y un enfoque gráfico-teorético utilizando componentes fuertemente conectados para la visibilidad pre-computación, así como la conexión entre los dos métodos. Se destacaron los árboles BSP como una estructura de búsqueda espacial independiente de dimensión, con aplicaciones para la determinación de superficie visible. La tesis también incluía los primeros datos empíricos que demostraban que el tamaño del árbol y el número de nuevos polígonos eran razonables (utilizando un modelo del transbordador espacial).
• 1983 Fuchs et al. describió una implementación de micro-código del algoritmo de árbol BSP en un sistema de amortiguación de marco Ikonas. Esta fue la primera demostración de determinación de superficie visible en tiempo real utilizando árboles BSP.
• 1987 Thibault y Naylor describieron cómo la poliédra arbitraria puede ser representada usando un árbol BSP en lugar de la tradicional b-rep (representación fronteriza). Esto proporcionó una representación sólida frente a una representación basada en la superficie. Se describieron las operaciones en polihedra utilizando una herramienta, permitiendo una geometría sólida constructiva (CSG) en tiempo real. Este fue el precursor del diseño de nivel BSP usando "brushes", introducido en el editor de Quake y recogido en el Editor Unreal.
• 1990 Naylor, Amanatides y Thibault proporcionaron un algoritmo para fusionar dos árboles BSP para formar un nuevo árbol BSP de los dos árboles originales. Esto proporciona muchos beneficios, incluyendo la combinación de objetos móviles representados por árboles BSP con un ambiente estático (también representado por un árbol BSP), operaciones CSG muy eficientes en polihedra, detección exacta de colisiones en O(log n * log n), y el orden adecuado de superficies transparentes contenidas en dos objetos interpenetrantes (ha sido utilizado para un efecto de visión de rayos X).
• 1990 Teller y Séquin propusieron la generación offline de conjuntos potencialmente visibles para acelerar la determinación de superficie visible en entornos ortogonales 2D.
• 1991 Gordon y Chen [CHEN91] describieron un método eficiente para realizar el renderizado frontal a espalda de un árbol BSP, en lugar del enfoque tradicional de espalda a frente. Utilizaron una estructura especial de datos para registrar, eficientemente, partes de la pantalla que se han dibujado, y las que aún no se han renderizado. Este algoritmo, junto con la descripción de BSP Trees en el libro de texto de gráficos de ordenador estándar del día (Gráficos informáticos: Principios y prácticas) fue utilizado por John Carmack en la fabricación de Doom (video juego).
• 1992 La tesis doctoral de Teller describió la eficiente generación de conjuntos potencialmente visibles como un paso previo al procesamiento para acelerar la determinación de superficie visible en tiempo real en entornos poligonales arbitrarios 3D. Esto fue usado en Quake y contribuyó significativamente a la actuación de ese juego.
• 1993 Naylor respondió la pregunta de lo que caracteriza un buen árbol BSP. Usó modelos de caso esperados (más que el peor análisis de casos) para medir matemáticamente el costo esperado de buscar un árbol y utilizó esta medida para construir buenos árboles BSP. Intuitivamente, el árbol representa un objeto en una forma multi-resolución (más exactamente, como un árbol de aproximaciones). Se dibujan paralelos con códigos Huffman y árboles probabilísticos de búsqueda binaria.
• 1993 La tesis doctoral de Hayder Radha describió (natural) métodos de representación de imagen usando árboles BSP. Esto incluye el desarrollo de un marco de construcción de árboles BSP óptimo para cualquier imagen de entrada arbitraria. Este marco se basa en una nueva transformación de imagen, conocida como la Línea de Partición (LSE) de menos espacio (LPE). La tesis de H. Radha también desarrolló un marco de compresión de imagen de distorsión de velocidad óptima (RD) y enfoques de manipulación de imágenes usando árboles BSP.

Referencias adicionales