Pársec

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Unidad de longitud utilizada en astronomía

El parsec (símbolo: pc) es una unidad de longitud utilizada para medir las grandes distancias a los objetos astronómicos fuera del Sistema Solar, aproximadamente igual a 3.26 años luz o 206,265 unidades astronómicas (au), es decir, 30.9 billones de kilómetros (19.2 billones de millas). La unidad de parsec se obtiene mediante el uso de paralaja y trigonometría, y se define como la distancia a la que 1 au subtendiere un ángulo de un árcsecond (1/3600 de un grado). Esto corresponde a 648000/ $π$ unidades astronómicas, es decir. ${displaystyle 1,mathrm {pc} =1/tan left({1} mathrm {arcsec} right),mathrm {au} }$ . La estrella más cercana, Proxima Centauri, es de aproximadamente 1,3 parsecs (4,2 años luz) del Sol. La mayoría de las estrellas visibles al ojo desnudo están dentro de unos pocos cientos de parsecs del Sol, con los más distantes a unos pocos miles.

La palabra parsec es un acrónimo de "paralaje de un segundo" y fue acuñado por el astrónomo británico Herbert Hall Turner en 1913 para facilitar a los astrónomos los cálculos de distancias astronómicas a partir de datos de observación sin procesar. En parte por esta razón, es la unidad preferida en astronomía y astrofísica, aunque el año luz sigue siendo prominente en los textos de divulgación científica y en el uso común. Aunque los parsecs se usan para las distancias más cortas dentro de la Vía Láctea, se requieren múltiplos de parsecs para las escalas más grandes del universo, incluidos los kiloparsecs (kpc) para los objetos más distantes dentro y alrededor de la Vía Láctea, los megaparsecs (Mpc) para las distancias medias. galaxias distantes y gigaparsecs (Gpc) para muchos cuásares y las galaxias más distantes.

En agosto de 2015, la Unión Astronómica Internacional (UAI) aprobó la Resolución B2 que, como parte de la definición de una escala de magnitud bolométrica aparente y absoluta estandarizada, mencionó una definición explícita existente del parsec como exactamente 648000/ $π$ au, o aproximadamente 3.0856775814913673×10¹⁶ metros (basado en la definición exacta SI de la unidad astronómica de IAU 2012). Esto corresponde a la definición de ángulo pequeño del parsec que se encuentra en muchas referencias astronómicas.

Historia y derivación

El parsec se define como igual a la longitud del cateto adyacente (el cateto opuesto es 1 AU) de un triángulo rectángulo imaginario extremadamente alargado en el espacio. Las dos dimensiones en las que se basa este triángulo son su cateto más corto, de una unidad astronómica de longitud (la distancia media entre la Tierra y el Sol), y el ángulo subtendido del vértice opuesto a ese cateto, que mide un segundo de arco. Aplicando las reglas de la trigonometría a estos dos valores, se puede derivar la unidad de longitud del otro cateto del triángulo (el parsec).

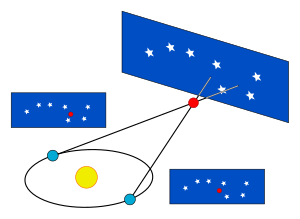
Uno de los métodos más antiguos que utilizan los astrónomos para calcular la distancia a una estrella es registrar la diferencia de ángulo entre dos mediciones de la posición de la estrella en el cielo. La primera medición se toma desde la Tierra en un lado del Sol, y la segunda se toma aproximadamente medio año después, cuando la Tierra está en el lado opuesto del Sol. La distancia entre las dos posiciones de la Tierra cuando se tomaron las dos medidas es el doble de la distancia entre la Tierra y el Sol. La diferencia de ángulo entre las dos medidas es el doble del ángulo de paralaje, que está formado por líneas desde el Sol y la Tierra hasta la estrella en el vértice distante. Luego, la distancia a la estrella podría calcularse usando trigonometría. Las primeras mediciones directas publicadas con éxito de un objeto a distancias interestelares fueron realizadas por el astrónomo alemán Friedrich Wilhelm Bessel en 1838, quien utilizó este enfoque para calcular la distancia de 3,5 parsec de 61 Cygni.

Moción de paralaja estelar de paralaja anual

La paralaje de una estrella se define como la mitad de la distancia angular que parece moverse una estrella en relación con la esfera celeste cuando la Tierra orbita alrededor del Sol. De manera equivalente, es el ángulo subtendido, desde la perspectiva de esa estrella, del semieje mayor de la órbita de la Tierra. La estrella, el Sol y la Tierra forman las esquinas de un triángulo rectángulo imaginario en el espacio: el ángulo recto es la esquina del Sol y la esquina de la estrella es el ángulo de paralaje. La longitud del lado opuesto al ángulo de paralaje es la distancia de la Tierra al Sol (definida como una unidad astronómica, au), y la longitud del lado adyacente da la distancia del sol a la estrella. Por lo tanto, dada una medida del ángulo de paralaje, junto con las reglas de la trigonometría, se puede encontrar la distancia del Sol a la estrella. Un parsec se define como la longitud del lado adyacente al vértice ocupado por una estrella cuyo ángulo de paralaje es un segundo de arco.

El uso del parsec como unidad de distancia se deriva naturalmente del método de Bessel, porque la distancia en parsecs se puede calcular simplemente como el recíproco del ángulo de paralaje en segundos de arco (es decir, si el ángulo de paralaje es 1 segundo de arco, el objeto está a 1 pc del Sol; si el ángulo de paralaje es de 0,5 segundos de arco, el objeto está a 2 pc de distancia, etc.). No se requieren funciones trigonométricas en esta relación porque los ángulos muy pequeños involucrados significan que se puede aplicar la solución aproximada del triángulo delgado.

Aunque puede haber sido usado antes, el término parsec se mencionó por primera vez en una publicación astronómica en 1913. El astrónomo real Frank Watson Dyson expresó su preocupación por la necesidad de un nombre para esa unidad de distancia.. Propuso el nombre astron, pero mencionó que Carl Charlier había sugerido siriómetro y Herbert Hall Turner había propuesto parsec. Fue la propuesta de Turner la que quedó.

Calcular el valor de un parsec

Según la definición de 2015, 1 au de longitud de arco subtiende un ángulo de 1″ en el centro del círculo de radio 1 ud. Es decir, 1 pc = 1 au/tan(1″) ≈ 206.264,8 au por definición. Convertir de unidades de grado/minuto/segundo a radianes,

{displaystyle {frac {1{text{ pc}}}{1{text{ au}}}}={frac {180times 60times 60}{pi }}}

, y

{displaystyle 1{text{ au}}=149,597,870,700{text{ m}}}

(exacto por la definición de 2012 de la au)

Por lo tanto,

{displaystyle pi ~mathrm {pc} =180times 60times 60~mathrm {au} =180times 60times 60times 149,597,870,700~mathrm {m} =96,939,420,213,600,000~mathrm {m} }

(exacto por la definición 2015)

Por lo tanto,

{displaystyle 1~mathrm {pc} ={frac {96,939,420,213,600,000}{pi }}~mathrm {m} =30,856,775,814,913,673~mathrm {m} }

Aproximadamente,

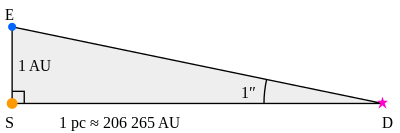
En el diagrama anterior (no a escala), S representa el Sol y E la Tierra en un punto de su órbita. Así, la distancia ES es una unidad astronómica (au). El ángulo SDE es un segundo de arco (1</3600 de un grado), por lo que, por definición, D es un punto en el espacio a una distancia de un parsec de el sol. Mediante trigonometría, la distancia SD se calcula de la siguiente manera:

{displaystyle {begin{aligned}mathrm {SD} &={frac {mathrm {ES} }{tan 1''}}\&={frac {mathrm {ES} }{tan left({frac {1}{60times 60}}times {frac {pi }{180}}right)}}\&approx {frac {1,mathrm {au} }{{frac {1}{60times 60}}times {frac {pi }{180}}}}={frac {648,000}{pi }},mathrm {au} approx 206,264.81~mathrm {au}.end{aligned}}}

Porque la unidad astronómica se define como 149597870700 m, se puede calcular lo siguiente:

Por lo tanto, 1 parsec	. 206264.806247096 unidades astronómicas
	. 3.085677581×10¹⁶ metros
	. 30.856775815kilómetros trillones
	. 19.173511577millas de trillón

Por lo tanto, si 1 ly ≈ 9,46×10¹⁵ m,

Entonces... 1 pc. 3.261563777ly

Un corolario establece que un parsec es también la distancia desde la que se debe ver un disco de una unidad astronómica de diámetro para que tenga un diámetro angular de un segundo de arco (colocando al observador en D y un diámetro del disco en ES).

Matemáticamente, para calcular la distancia, dadas las medidas angulares obtenidas de los instrumentos en segundos de arco, la fórmula sería:

{displaystyle {text{Distance}}_{text{star}}={frac {{text{Distance}}_{text{earth-sun}}}{tan {frac {theta }{3600}}}}}

donde θ es el ángulo medido en segundos de arco, Distancia_tierra-sol es una constante (1 au o 1,5813×10⁻⁵ ly). La distancia estelar calculada estará en la misma unidad de medida utilizada en Distancia_tierra-sol (por ejemplo, si Distancia_tierra-sol = 1 au, la unidad para Distancia_estrella está en unidades astronómicas; si Distancia_tierra-sol = 1.5813×10⁻⁵ ly, la unidad para Distancia_estrella es en años luz).

La longitud del parsec utilizado en la Resolución B2 de la IAU 2015 (exactamente 648000/ $π$ unidades astronómicas) corresponde exactamente a la derivada utilizando el cálculo de ángulo pequeño. Esto difiere de la definición clásica de tangente inversa en aproximadamente 200 km, es decir, solo después de la 11.ª cifra significativa. Como la unidad astronómica fue definida por la IAU (2012) como una longitud SI exacta en metros, ahora el parsec corresponde a una longitud SI exacta en metros. Al metro más cercano, el parsec de ángulo pequeño corresponde a 30856775814913673 m.

Uso y medición

El método de paralaje es el paso de calibración fundamental para la determinación de distancias en astrofísica; sin embargo, la precisión de las mediciones del ángulo de paralaje del telescopio terrestre está limitada a aproximadamente 0.01″, y por lo tanto, a estrellas no más de 100 pc de distancia. Esto se debe a que la atmósfera de la Tierra limita la nitidez de la imagen de una estrella. Los telescopios espaciales no están limitados por este efecto y pueden medir con precisión las distancias a los objetos más allá del límite de las observaciones terrestres. Entre 1989 y 1993, el satélite Hipparcos, lanzado por la Agencia Espacial Europea (ESA), midió paralajes durante aproximadamente 100000 estrellas con una precisión astrométrica de aproximadamente 0.97 mas, y obtuvo mediciones precisas para distancias estelares de estrellas hasta 1000 pc de distancia.

El satélite Gaia de la ESA, que se lanzó el 19 de diciembre de 2013, está destinado a medir mil millones de distancias estelares dentro de 20 microarcosegundo, lo que produce errores del 10 % en las mediciones hasta el Centro Galáctico, aproximadamente 8000 pc de distancia en la constelación de Sagitario.

Distancias en parsecs

Distancias inferiores a un parsec

Las distancias expresadas en fracciones de parsec generalmente involucran objetos dentro de un solo sistema estelar. Así por ejemplo:

Una unidad astronómica (au), la distancia del Sol a la Tierra, está bajo 5×10⁻⁶pc.
La sonda espacial más distante, Voyager 1, estaba 0,000703pc desde la Tierra hasta enero de 2019. Voyager 1 Tomó 41 años para cubrir esa distancia.
Se calcula que la nube Oort es aproximadamente 0.6 pc de diámetro

Como observó el Telescopio Espacial Hubble, el jet astrofísico que estalló del núcleo galáctico activo de los subtendientes M87 20′′ y se cree que son 1.5 kiloparsecs (4.892 ly) de largo (el jet es un poco precavido desde la perspectiva de la Tierra).

Parsecs y kiloparsecs

Las distancias expresadas en parsecs (pc) incluyen distancias entre estrellas cercanas, como aquellas en el mismo brazo espiral o cúmulo globular. Una distancia de 1000 parsecs (3262 ly) se indica con el kiloparsec (kpc). Los astrónomos suelen utilizar kiloparsecs para expresar distancias entre partes de una galaxia o dentro de grupos de galaxias. Entonces, por ejemplo (NB, un parsec es aproximadamente igual a 3.26 años luz):

Proxima Centauri, la estrella conocida más cercana a la tierra que no sea el sol, está a unos 1.3 parsecs (4.24 ly) de distancia, por medición directa del paralaje.
La distancia al clúster abierto Pleiades es 130±10 pc ()420±30 ly) de nosotros, por Hipparcos Medición de paralaja.
El centro de la Vía Láctea está a más de 8 kiloparsecs (26.000 ly) de la Tierra, y la Vía Láctea tiene aproximadamente 34 kiloparsecs (110.000 ly) de ancho.
La galaxia Andromeda (M31) está a unos 780 kpc (2,5 millones de ly) de la Tierra.

Megaparsecs y gigaparsecs

Los astrónomos suelen expresar las distancias entre las galaxias vecinas y los cúmulos de galaxias en megaparsecs (Mpc). Un megaparsec es un millón de parsecs, o unos 3.260.000 años luz. A veces, las distancias galácticas se dan en unidades de Mpc/h (como en "50/h Mpc", también escrito "50 Mpc h⁻¹"). h es una constante (la "constante de Hubble adimensional") en el rango 0.5 < h < 0,75 reflejando la incertidumbre en el valor de la constante de Hubble H para la tasa de expansión del universo: h = H/100 (km/s)/Mpc. La constante de Hubble se vuelve relevante cuando se convierte un corrimiento al rojo observado z en una distancia d usando la fórmula d ≈ c/H × z.

Un gigaparsec (Gpc) es mil millones de parsecs, una de las unidades de longitud más grandes comúnmente utilizadas. Un gigaparsec equivale a unos 3260 millones, o aproximadamente 1/14 de la distancia al horizonte del universo observable (dictada por la radiación cósmica de fondo). Los astrónomos suelen utilizar gigaparsecs para expresar los tamaños de estructuras a gran escala, como el tamaño y la distancia a la Gran Muralla CfA2; las distancias entre cúmulos de galaxias; y la distancia a los cuásares.

Por ejemplo:

La galaxia Andromeda es de aproximadamente 0,78 Mpc (2,5 millones de li) de la Tierra.
El cúmulo de galaxias más grande, el cúmulo de Virgo, es alrededor de 16.5 Mpc (54 millones de ly) de la Tierra.
La galaxia RXJ1242-11, observada para tener un agujero negro supermasivo similar al de la Vía Láctea, es de unos 200 Mpc (650 millones ly) de la Tierra.
El filamento de galaxias Hércules–Corona Borealis Great Wall, actualmente la estructura más grande conocida del universo, es alrededor de 3 Gpc (9.8 mil millones de ly) a través.
El horizonte de partículas (el límite del universo observable) tiene un radio de alrededor de 14 Gpc (46 mil millones ly).

Unidades de volumen

Para determinar el número de estrellas en la Vía Láctea, se seleccionan volúmenes en kiloparsecs cúbicos (kpc³) en varias direcciones. Se cuentan todas las estrellas de estos volúmenes y se determina estadísticamente el número total de estrellas. El número de cúmulos globulares, nubes de polvo y gas interestelar se determina de manera similar. Para determinar el número de galaxias en los supercúmulos, se seleccionan volúmenes en megaparsecs cúbicos (Mpc³). Todas las galaxias en estos volúmenes están clasificadas y contabilizadas. El número total de galaxias puede entonces determinarse estadísticamente. El enorme vacío de Bootes se mide en megaparsecs cúbicos.

En cosmología física, se seleccionan volúmenes de gigaparsecs cúbicos (Gpc³) para determinar la distribución de la materia en el universo visible y para determinar el número de galaxias y cuásares. El Sol es actualmente la única estrella en su parsec cúbico (pc³), pero en los cúmulos globulares la densidad estelar podría ser de 100–1000 pc⁻³.

El volumen de observación de los interferómetros de ondas gravitacionales (por ejemplo, LIGO, Virgo) se expresa en términos de megaparsecs cúbicos (Mpc³) y es esencialmente el valor de la distancia efectiva al cubo.

En la cultura popular

Al parecer, Han Solo utilizó incorrectamente el parsec como medida del tiempo en la primera película de Star Wars, cuando reclamó su nave, el Millennium Falcon "realizó la Carrera de Kessel en menos de 12 parsecs". La afirmación se repitió en The Force Awakens, pero se reconectó en Solo: A Star Wars Story, al afirmar que el Millennium Falcon viajó una distancia más corta. (a diferencia de un tiempo más rápido) debido a una ruta más peligrosa a través del hiperespacio, habilitada por su velocidad y maniobrabilidad. También se usa de forma ambigua como unidad espacial en The Mandalorian.

En el libro Una arruga en el tiempo, "Megaparsec" es el apodo del Sr. Murry para su hija Meg.

Contenido relacionado

Más resultados...