Pares clasificados

Los pares clasificados o método Tideman es un sistema electoral desarrollado en 1987 por Nicolaus Tideman que selecciona a un único ganador mediante votos que expresan preferencias. RP también se puede utilizar para crear una lista ordenada de ganadores.

Si hay un candidato que es preferido sobre los demás candidatos, cuando se compara a su vez con cada uno de los demás, RP garantiza que ese candidato ganará. Debido a esta propiedad, RP es, por definición, un método de Condorcet.

Procedimiento

w - x - z - y	7 papeletas
w - y - x - z	2 papeletas
x - y - z - w	4 papeletas
x - z - w - y	5 papeletas
y - w - x - z	1 papeletas
y - z - w - x	8 papeletas

El procedimiento de RP (Par clasificado) es el siguiente:

1. Cuente el conteo de votos comparando cada par de candidatos y determine el ganador de cada par (siempre que no haya un empate)
2. Ordene (clasifique) cada par, por la mayor fuerza de la victoria, primero a la más pequeña, al final.
3. "Bloquear" cada par, comenzando por el que tenga el mayor número de votos ganadores, y agregar uno por turno a un gráfico siempre que no creen un ciclo (lo que crearía una ambigüedad). El gráfico completo muestra al ganador.

El procedimiento se puede ilustrar con un ejemplo sencillo. Suponga que hay 27 votantes y 4 candidatos w, x, y y z tales que los votos se emiten como se muestra en la tabla de papeletas.

Cuenta

	w	X	y	z
w	–	9	1	–7
X	–9	–	5	11
y	–1	–5	–	3
z	7	–11	-3	–

El conteo de votos se puede expresar como una tabla en la que la entrada (w, x  ) es el número de papeletas en las que w es mayor que x menos el número en el que x es mayor que w. En el ejemplo, w es más alto que x en las dos primeras filas y las dos últimas filas de la mesa de votación (un total de 18 papeletas), mientras que x es más alto que w en las dos filas del medio (un total de 9), por lo que la entrada en (w, x  ) celda es 18–9 = 9.

Observe la simetría sesgada de la mesa.

(x, z  )11

(w, x  )9

(z, w  )7

(x, y  )5

(y, z  )3

(w, y  )1

Clasificar

Las mayorías positivas se ordenan luego en orden decreciente de magnitud:

Cerrar con llave

	w	X	y	z
w	0	1	0	1
X	–1	0	0	1
y	0	0	0	0
z	–1	–1	0	0

La siguiente etapa es examinar las mayorías por turnos para determinar qué pares "bloquear". Esto se puede hacer construyendo una matriz en la que la entrada (x, y  ) sea inicialmente 0, y se establezca en 1 si decidimos que se prefiere x a y y a –1 si decidimos que se prefiere y a x. Estas preferencias se deciden por lista de mayorías ordenadas, saltándose simplemente aquellas que sean incompatibles con decisiones anteriores.

Las dos primeras mayorías nos dicen que se prefiere x a z y w a x, de lo que se sigue por transitividad que se prefiere w a z. Una vez que estos hechos se han incorporado a la tabla, toma la forma que se muestra después de dos pasos. Observe de nuevo la simetría sesgada.

	w	X	y	z
w	0	1	1	1
X	–1	0	1	1
y	–1	–1	0	0
z	–1	–1	0	0

La tercera mayoría nos dice que se prefiere z a w, pero como ya hemos decidido que se prefiere w a z, la ignoramos.

La cuarta mayoría nos dice que se prefiere x a y, y como sabemos que se prefiere w a x, inferimos que se prefiere w a y, dándonos la tabla después de 4 pasos.

	w	X	y	z
w	0	1	1	1
X	–1	0	1	1
y	–1	–1	0	1
z	–1	–1	–1	0

La quinta mayoría nos dice que se prefiere y a z, y esto completa la tabla.

Ganador

En el gráfico resultante de los pares bloqueados, la fuente corresponde al ganador. En este caso, se prefiere w a todos los demás candidatos y, por lo tanto, se identifica como el ganador.

Mayorías empatadas

En el ejemplo las mayorías son todas diferentes, y esto es lo que suele pasar cuando el número de votantes es grande. Si los empates son poco probables, entonces no importa mucho cómo se resuelvan, por lo que se puede hacer una elección aleatoria. Sin embargo, este no es el procedimiento de Tideman, que es considerablemente más complicado. Ver su papel para más detalles.

Un ejemplo

La situación

• v
• t
• mi

Imagine que Tennessee tiene una elección sobre la ubicación de su capital. La población de Tennessee se concentra en torno a sus cuatro ciudades principales, que están repartidas por todo el estado. Para este ejemplo, suponga que todo el electorado vive en estas cuatro ciudades y que todos quieren vivir lo más cerca posible de la capital.

Los candidatos a la capital son:

• Memphis, la ciudad más grande del estado, con el 42% de los votantes, pero ubicada lejos de las demás ciudades
• Nashville, con el 26% de los votantes, cerca del centro del estado
• Knoxville, con el 17% de los votantes
• Chattanooga, con el 15% de los votantes

Las preferencias de los votantes se dividirían así:

42% de los votantes(cerca de Memphis)	26% de los votantes(cerca de Nashville)	15% de los votantes(cerca de Chattanooga)	17% de los votantes(cerca de Knoxville)
MenfisNashvilleChattanoogaknoxville	NashvilleChattanoogaknoxvilleMenfis	ChattanoogaknoxvilleNashvilleMenfis	knoxvilleChattanoogaNashvilleMenfis

Los resultados se tabularían de la siguiente manera:

	UN
Menfis	Nashville	Chattanooga	knoxville
B	Menfis		[A] 58 %[B] 42 %	[A] 58 %[B] 42 %	[A] 58 %[B] 42 %
Nashville	[A] 42 %[B] 58 %		[A] 32 %[B] 68 %	[A] 32 %[B] 68 %
Chattanooga	[A] 42 %[B] 58 %	[A] 68 %[B] 32 %		[A] 17 %[B] 83 %
knoxville	[A] 42 %[B] 58 %	[A] 68 %[B] 32 %	[A] 83 %[B] 17 %
Resultados de las elecciones por pares (ganado-perdido-empatado):	0-3-0	3-0-0	2-1-0	1-2-0
Votos en contra en la peor derrota por parejas:	58%	N / A	68%	83%

• [A] indica los votantes que prefirieron al candidato que figura en el título de la columna al candidato que figura en el título de la fila
• [B] indica los votantes que prefirieron al candidato que figura en el título de la fila al candidato que figura en el título de la columna

Cuenta

Primero, enumere cada par y determine el ganador:

Par	Ganador
Menfis (42 %) frente a Nashville (58 %)	Nashville 58%
Menfis (42 %) frente a Chattanooga (58 %)	Chattanooga 58%
Menfis (42 %) frente a Knoxville (58 %)	58%
Nashville (68 %) frente a Chattanooga (32 %)	Nashville 68%
Nashville (68 %) frente a Knoxville (32 %)	Nashville 68%
Chattanooga (83 %) frente a Knoxville (17 %)	Chattanooga: 83%

Tenga en cuenta que se pueden utilizar recuentos absolutos de votos o porcentajes del número total de votos; no hace ninguna diferencia ya que lo que importa es la proporción de votos entre dos candidatos.

Clasificar

Luego se ordenan los votos. La mayoría más grande es "Chattanooga sobre Knoxville"; El 83% de los votantes prefieren Chattanooga. Por lo tanto, los pares de arriba se ordenarían de esta manera:

Par	Ganador
Chattanooga (83 %) frente a Knoxville (17 %)	Chattanooga 83%
Nashville (68 %) frente a Knoxville (32 %)	Nashville 68%
Nashville (68 %) frente a Chattanooga (32 %)	Nashville 68%
Menfis (42 %) frente a Nashville (58 %)	Nashville 58%
Menfis (42 %) frente a Chattanooga (58 %)	Chattanooga 58%
Menfis (42 %) frente a Knoxville (58 %)	58%

Cerrar con llave

Luego, los pares se bloquean en orden, omitiendo cualquier par que cree un ciclo:

• Cierra Chattanooga sobre Knoxville.
• Cierra Nashville sobre Knoxville.
• Bloquear Nashville sobre Chattanooga.
• Cierra Nashville sobre Memphis.
• Cierra Chattanooga sobre Memphis.
• Cierra Knoxville sobre Memphis.

En este caso, ninguno de los pares crea ciclos, por lo que todos y cada uno de ellos están bloqueados.

Cada "bloqueo" agregaría otra flecha al gráfico que muestra la relación entre los candidatos. Aquí está el gráfico final (donde las flechas apuntan lejos del ganador).

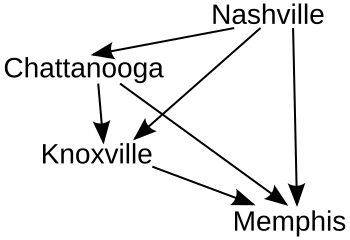
En este ejemplo, Nashville es el ganador usando RP, seguido por Chattanooga, Knoxville y Memphis en segundo, tercer y cuarto lugar respectivamente.

Resumen

En la elección de ejemplo, el ganador es Nashville. Esto sería cierto para cualquier método Condorcet.

Usando la votación First-past-the-post y algunos otros sistemas, Memphis habría ganado la elección al tener la mayor cantidad de personas, a pesar de que Nashville ganó todas las elecciones simuladas por parejas. El uso de la votación de segunda vuelta instantánea en este ejemplo daría como resultado que Knoxville ganara aunque más personas prefirieran Nashville sobre Knoxville.

Criterios

De los criterios de votación formales, el método de pares clasificados supera el criterio de la mayoría, el criterio de monotonicidad, el criterio de Smith (que implica el criterio de Condorcet), el criterio del perdedor de Condorcet y el criterio de independencia de los clones. Las parejas clasificadas no cumplen el criterio de consistencia ni el criterio de participación. Si bien los pares clasificados no son completamente independientes de las alternativas irrelevantes, aún satisfacen la independencia local de las alternativas irrelevantes.

Independencia de alternativas irrelevantes

Los pares clasificados fallan la independencia de las alternativas irrelevantes. Sin embargo, el método se adhiere a una propiedad menos estricta, a veces denominada independencia de las alternativas dominadas por Smith (ISDA). Dice que si un candidato (X) gana una elección y se agrega una nueva alternativa (Y), X ganará la elección si Y no está en el conjunto de Smith. ISDA implica el criterio de Condorcet.

Tabla de comparación

La siguiente tabla compara los pares clasificados con otros métodos preferenciales de elección de un solo ganador:

Sistema	monótono	Ganador de Condorcet	Mayoria	perdedor de Condorcet	perdedor de la mayoría	mayoría mutua	Herrero	ISDA	LIIA	Independencia de los clones	simetría inversa	Participación, consistencia	Más tarde sin daños	Más tarde sin ayuda	Tiempo polinomial	Resolubilidad
Schulze	Sí	Sí	Sí	Sí	Sí	Sí	Sí	Sí	No	Sí	Sí	No	No	No	Sí	Sí
parejas clasificadas	Sí	Sí	Sí	Sí	Sí	Sí	Sí	Sí	Sí	Sí	Sí	No	No	No	Sí	Sí
Alternativa de Tideman	No	Sí	Sí	Sí	Sí	Sí	Sí	Sí	No	Sí	No	No	No	No	Sí	Sí
Kemeny-Joven	Sí	Sí	Sí	Sí	Sí	Sí	Sí	Sí	Sí	No	Sí	No	No	No	No	Sí
Copelandia	Sí	Sí	Sí	Sí	Sí	Sí	Sí	Sí	No	No	Sí	No	No	No	Sí	No
Nanson	No	Sí	Sí	Sí	Sí	Sí	Sí	No	No	No	Sí	No	No	No	Sí	Sí
Negro	Sí	Sí	Sí	Sí	Sí	No	No	No	No	No	Sí	No	No	No	Sí	Sí
Votación de segunda vuelta instantánea	No	No	Sí	Sí	Sí	Sí	No	No	No	Sí	No	No	Sí	Sí	Sí	Sí
Smith/IRV	No	Sí	Sí	Sí	Sí	Sí	Sí	Sí	No	Sí	No	No	No	No	Sí	Sí
Borda	Sí	No	No	Sí	Sí	No	No	No	No	No	Sí	Sí	No	Sí	Sí	Sí
balduino	No	Sí	Sí	Sí	Sí	Sí	Sí	No	No	No	No	No	No	No	Sí	Sí
Bucklin	Sí	No	Sí	No	Sí	Sí	No	No	No	No	No	No	No	Sí	Sí	Sí
Pluralidad	Sí	No	Sí	No	No	No	No	No	No	No	No	Sí	Sí	Sí	Sí	Sí
voto contingente	No	No	Sí	Sí	Sí	No	No	No	No	No	No	No	Sí	Sí	Sí	Sí
coombs	No	No	Sí	Sí	Sí	Sí	No	No	No	No	No	No	No	No	Sí	Sí
minimax	Sí	Sí	Sí	No	No	No	No	No	No	No	No	No	No	No	Sí	Sí
Anti-pluralidad	Sí	No	No	No	Sí	No	No	No	No	No	No	Sí	No	No	Sí	Sí
Voto contingente de Sri Lanka	No	No	Sí	No	No	No	No	No	No	No	No	No	Sí	Sí	Sí	Sí
voto suplementario	No	No	Sí	No	No	No	No	No	No	No	No	No	Sí	Sí	Sí	Sí
dodgson	No	Sí	Sí	No	No	No	No	No	No	No	No	No	No	No	No	Sí