Pareja Tusi

El par de Tusi (también conocido como el mecanismo de Tusi) es un dispositivo matemático en el que un círculo pequeño gira dentro de un círculo más grande cuyo diámetro es el doble del del círculo más pequeño. Las rotaciones de los círculos hacen que un punto de la circunferencia del círculo más pequeño oscile hacia adelante y hacia atrás en un movimiento lineal a lo largo del diámetro del círculo más grande. El par de Tusi es un hipocicloide de 2 cúspides.

La pareja fue propuesta por primera vez por el astrónomo y matemático persa del siglo XIII Nasir al-Din al-Tusi en su Tahrir al-Majisti (Comentario al Almagesto) de 1247 como una solución para el movimiento latitudinal de los planetas inferiores y luego utilizada ampliamente como sustituto del ecuante introducido más de mil años antes en el Almagesto de Ptolomeo.

La traducción de la copia de la descripción original del modelo geométrico de Tusi alude al menos a una inversión del modelo que se puede ver en los diagramas:

Si dos círculos coplanar, el diámetro de uno de los cuales es igual a la mitad del diámetro del otro, se toman para ser internamente tangente en un punto, y si se toma un punto en el círculo más pequeño — y dejar que sea en el punto de la tangencia— y si los dos círculos se mueven con movimientos simples en dirección opuesta de tal manera que el movimiento del [circle] más pequeño es dos veces el diámetro de cada rotación

La descripción no es coherente y parece combinar arbitrariamente características de varias inversiones posibles e imposibles del modelo geométrico.

Algebraicamente, el modelo se puede expresar con números complejos como

${\displaystyle \left(1-{2}\right)e^{i\theta }-{\frac {1} {2}e^{-i\theta }=i\,\sin \theta.}$

Otros comentaristas han observado que el par de Tusi puede interpretarse como una curva rodante donde la rotación del círculo interior satisface una condición de no deslizamiento a medida que su punto tangente se mueve a lo largo del círculo exterior fijo.

El término "pareja de Tusi" es moderno, acuñado por Edward Stewart Kennedy en 1966. Es uno de los varios dispositivos astronómicos islámicos tardíos que guardan una sorprendente similitud con los modelos de De revolutionibus de Nicolás Copérnico, incluido su modelo de Mercurio y su teoría de la trepidación. Los historiadores sospechan que Copérnico u otro autor europeo tuvieron acceso a un texto astronómico árabe, pero aún no se ha identificado una cadena exacta de transmisión. Se ha sugerido al científico y viajero del siglo XVI Guillaume Postel como un posible facilitador.

Dado que Copérnico utilizó el par de Tusi en su reformulación de la astronomía matemática, existe un creciente consenso sobre la idea de que de alguna manera se dio cuenta de esta idea. Se ha sugerido que la idea del par de Tusi puede haber llegado a Europa dejando pocos rastros manuscritos, ya que podría haber ocurrido sin la traducción de ningún texto árabe al latín. Una posible vía de transmisión puede haber sido a través de la ciencia bizantina; Gregorio Chioniades tradujo algunas de las obras de al-Tusi del árabe al griego bizantino. Varios manuscritos griegos bizantinos que contienen el par de Tusi todavía existen en Italia. Otra posibilidad es que se encontrara con el manuscrito del "Enderezamiento de las curvas" (Sefer Meyasher 'Aqov) mientras estudiaba en Italia.

Existen otras fuentes para este modelo matemático que permite convertir los movimientos circulares en movimientos lineales alternativos. Se encuentra en el Comentario al primer libro de Euclides de Proclo y el concepto era conocido en París a mediados del siglo XIV. En sus Questiones sobre la esfera (escritas antes de 1362), Nicole Oresme describió cómo combinar movimientos circulares para producir un movimiento lineal alternativo de un planeta a lo largo del radio de su epiciclo. La descripción de Oresme no es clara y no se sabe con certeza si se trata de una invención independiente o de un intento de abordar un texto árabe poco comprendido.

Aunque el par de Tusi se desarrolló en un contexto astronómico, matemáticos e ingenieros posteriores desarrollaron versiones similares de lo que se denominó mecanismos rectilíneos hipocicloides. El matemático Gerolamo Cardano diseñó un sistema conocido como movimiento de Cardan (también conocido como engranaje de Cardan). Los ingenieros del siglo XIX James White y Matthew Murray, así como diseñadores posteriores, desarrollaron aplicaciones prácticas del mecanismo rectilíneo hipocicloide.

En 2021, John Goodman desarrolló una versión práctica y mecánicamente sencilla del par Tusi, que evita el uso de un engranaje de borde externo, para proporcionar un movimiento lineal. Utiliza 3 engranajes rectos estándar. Un brazo giratorio (azul) está montado en un eje central, al que se monta un engranaje fijo (amarillo). Un engranaje loco (rojo) en el brazo engrana con el engranaje fijo. Un tercer engranaje (verde) engrana con el loco. El tercer engranaje tiene la mitad del número de dientes del engranaje fijo. Un brazo (naranja) está fijado al tercer engranaje. Si la longitud del brazo es igual a la distancia entre los engranajes fijo y exterior = d, el brazo describirá una línea recta de recorrido = 2d. Una ventaja de este diseño es que, si se utilizan engranajes de módulo estándar que no proporcionan el recorrido requerido, el engranaje loco no tiene que ser colineal con los otros dos engranajes.

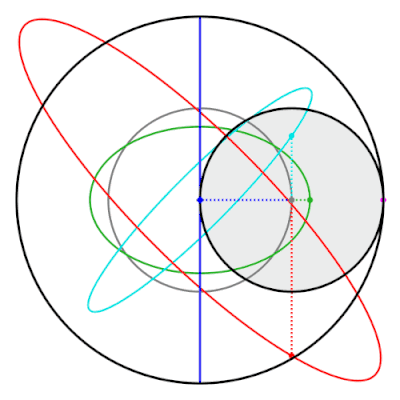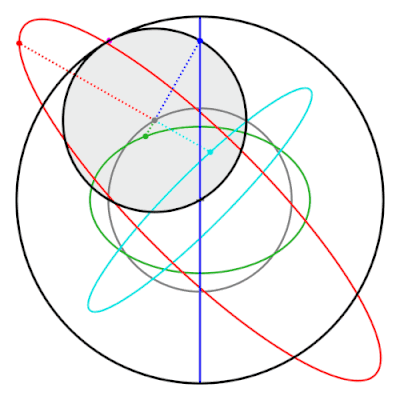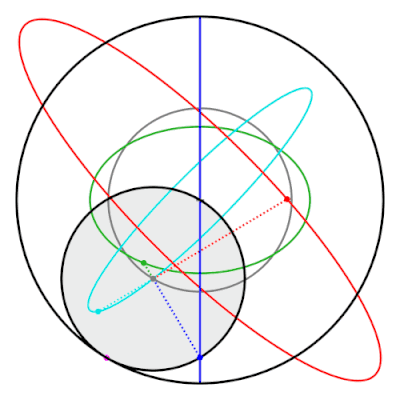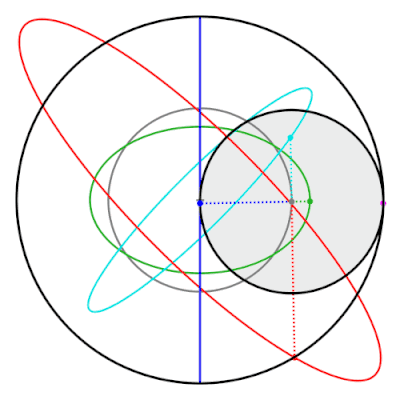
Una propiedad del par de Tusi es que los puntos del círculo interior que no están en la circunferencia trazan elipses. Estas elipses, y la línea recta trazada por el par de Tusi clásico, son casos especiales de hipotrocoides.

• Hypocycloidal de Murray Motor, utilizando una pareja Tusi como sustituto de guías crosshead o movimiento paralelo
• Engranaje epicíclico
• Mecanismo de línea recta
• Spirograph
• El torno geométrico
• Guilloché
• Curva delgada

• Di Bono, Mario (1995). "Copernicus, Amico, Fracastoro y Dispositivo de Tusi: Observaciones sobre el uso y la transmisión de un modelo". Journal for the History of Astronomy. 26 (2): 133–154. Bibcode:1995JHA ....26..133D. doi:10.1177/002182869502600203. S2CID 118330488.
• Kennedy, E. S. (1966). "Teoría Planetaria Medieval tardía". Isis. 57 (3): 365-378. doi:10.1086/350144. S2CID 143569912.
• Kren, Claudia (1971). "El dispositivo de rodamiento de Nasir al-Dîn al-Thūsī en el De spera de Nicole Oresme". Isis. 62 (4): 490-498. doi:10.1086/350791. S2CID 144526697.
• Ragep, F. J. "Las dos versiones de la pareja Tusi", en Del Deferente al Ecuador: un volumen de estudios en la historia de la ciencia en el antiguo y medieval Cercano Oriente en honor de E. S. Kennedy, Ed. David King y George Saliba, Annals de la Academia de Ciencias de Nueva York, 500. Academia de Ciencias de Nueva York, 1987. ISBN 0-89766-396-9 (pbk.)
• Ragep, F. J. El "Memoir on Astronomy" de Nasir al-Din al-Tusi Fuentes en la Historia de las Matemáticas y Ciencias Físicas12. 2 vols. Berlín/Nueva York: Springer, 1993. ISBN 3-540-94051-0 / ISBN 0-387-94051-0.

• Dennis W. Duke, Animaciones del Modelo Planetario Antiguo incluye dos enlaces de interés:
  • Una pareja Tusi interactiva
  • Modelos árabes para reemplazar el Ecuador
• George Saliba, "¿De quién es la ciencia árabe en Europa renacentista?" Discuti el modelo de Nasir al-Din al-Tusi y las interacciones de los astrónomos árabes, griegos y latinos.