Paralelepípedo

Parallelepiped
Tipo	Prism Plesiohedron
Caras	6 paralelogramas
Edges	12
Vertices	8
Grupo de Symmetry	Ci, [2]+,2+], (×), orden 2
Propiedades	convex, zonohedron

En geometría, un paralelepípedo es una figura tridimensional formada por seis paralelogramos (el término romboide también se usa a veces con este significado). Por analogía, se relaciona con un paralelogramo tal como un cubo se relaciona con un cuadrado. En geometría euclidiana, los cuatro conceptos—paralelepípedo y cubo en tres dimensiones, paralelogramo y cuadrado en dos dimensiones— están definidos, pero en el contexto de una geometría afín más general, en la que los ángulos no están diferenciados, solo existen paralelogramos y paralelepípedos. Tres definiciones equivalentes de paralelepípedo son

• un poliedro con seis caras (hexahedron), cada una de las cuales es un paralelograma,
• un hexahedro con tres pares de caras paralelas, y
• un prisma de que la base es un paralelograma.

El ortoedro rectangular (seis caras rectangulares), el cubo (seis caras cuadradas) y el romboedro (seis caras de rombo) son casos específicos de paralelepípedo.

"Paralelepípedo" ahora se suele pronunciar o; tradicionalmente era PARR-ə-lel-EP-ih-ped de acuerdo con su etimología en griego παραλληλεπίπεδον paralelepipedón, un cuerpo "que tiene planos paralelos".

Los paralelepípedos son una subclase de los prismatoides.

Propiedades

Cualquiera de los tres pares de caras paralelas se puede ver como los planos base del prisma. Un paralelepípedo tiene tres juegos de cuatro aristas paralelas; los bordes dentro de cada conjunto tienen la misma longitud.

Los paralelepípedos resultan de transformaciones lineales de un cubo (para los casos no degenerados: las transformaciones lineales biyectivas).

Dado que cada cara tiene simetría puntual, un paralelepípedo es un zonoedro. Además, todo el paralelepípedo tiene simetría puntual C_i (ver también triclínica). Cada cara es, vista desde fuera, la imagen especular de la cara opuesta. Las caras son en general quirales, pero el paralelepípedo no lo es.

Es posible un mosaico que llena el espacio con copias congruentes de cualquier paralelepípedo.

Volumen

Paralepípedo, generado por tres vectores

Un paralelepípedo puede considerarse como un prisma oblicua con un paralelograma como base. Por lo tanto el volumen V{displaystyle V} de un paralelepípedo es el producto del área base B{displaystyle B} y la altura h{displaystyle h} (ver diagrama). Con

• B=SilencioaSilencio⋅ ⋅ SilenciobSilencio⋅ ⋅ pecado⁡ ⁡ γ γ =Silencioa× × bSilencio{displaystyle B=left WordPressmathbf {a}derechocdot left habitmathbf {b} derecha vidacdot sin gamma =left perpetuamathbf {a} times mathbf {b} right sometida}} (donde) γ γ {displaystyle gamma } es el ángulo entre vectores a{displaystyle mathbf {a} y b{displaystyle mathbf {b}), y
• h=SilenciocSilencio⋅ ⋅ Silencio#⁡ ⁡ Silencio Silencio Silencio{displaystyle h=left durablemathbf {c} right sometidacdot left sometidacos theta right sometida} (donde) Silencio Silencio {displaystyle theta } es el ángulo entre vector c{displaystyle mathbf {c} y lo normal a la base), uno consigue:

V=B⋅ ⋅ h=()SilencioaSilencioSilenciobSilenciopecado⁡ ⁡ γ γ )⋅ ⋅ SilenciocSilencioSilencio#⁡ ⁡ Silencio Silencio Silencio=Silencioa× × bSilencioSilenciocSilencioSilencio#⁡ ⁡ Silencio Silencio Silencio=Silencio()a× × b)⋅ ⋅ cSilencio.{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {b} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft} {fnMicrosoft}

a=()a1,a2,a3)T,b=()b1,b2,b3)T,c=()c1,c2,c3)T,{fnMicrosoft Sans Serif}

V=SilencioDet[a1b1c1a2b2c2a3b3c3]Silencio.{begin{bmatrix}a_{2}a_{2}a_{3} {3} â3} {3}a_{3}a_{2} {2} {2}a_{2}a_}a_{3} {3} {3}}}}end{bmatrix}}}}derech}

()V1)

Otra manera de probar ()V1) es utilizar el componente de escalar en la dirección a× × b{displaystyle mathbf {a} times mathbf {b} vector c{displaystyle mathbf {c}:

V=Silencioa× × bSilencioSilencioEscalaa× × b⁡ ⁡ cSilencio=Silencioa× × bSilencioSilencio()a× × b)⋅ ⋅ cSilencioSilencioa× × bSilencio=Silencio()a× × b)⋅ ⋅ cSilencio.{displaystyle {begin{aligned}V=left arrestmathbf {a} times mathbf {b} right sobre la vidaleft sobre la vida útil {scal} _{mathbf {a} times mathbf {b} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif}

Una representación alternativa del volumen utiliza propiedades geométricas (ángulos y longitudes de los bordes) únicamente:

V=abc1+2#⁡ ⁡ ()α α )#⁡ ⁡ ()β β )#⁡ ⁡ ()γ γ )− − #2⁡ ⁡ ()α α )− − #2⁡ ⁡ ()β β )− − #2⁡ ⁡ ()γ γ ),{displaystyle V=abc{sqrt {1+2cos(alpha)cos(beta)cos(gamma)-cos ^{2}(alpha)-cos ^{2}(beta)-cos ^{2}(gamma)}}}}}}}}}

()V2)

Donde α α =∠ ∠ ()b,c){displaystyle alpha =angle (mathbf {b}mathbf {c}}, β β =∠ ∠ ()a,c){displaystyle beta =angle (mathbf {a}mathbf {c}}, γ γ =∠ ∠ ()a,b){displaystyle gamma =angle (mathbf {a}mathbf {b})}, y a,b,c{displaystyle a,b,c} son las longitudes del borde.

Prueba de (V2)

La prueba de ()V2) utiliza propiedades de un determinante y la interpretación geométrica del producto del punto:

Vamos. M{displaystyle M} el 3×3-matrix, cuyas columnas son los vectores a,b,c{displaystyle mathbf {a}mathbf {b}Mathbf {c} (véase supra). Entonces lo siguiente es cierto:

V2=()DetM)2=DetMDetM=DetMTDetM=Det()MTM)=Det[a⋅ ⋅ aa⋅ ⋅ ba⋅ ⋅ cb⋅ ⋅ ab⋅ ⋅ bb⋅ ⋅ cc⋅ ⋅ ac⋅ ⋅ bc⋅ ⋅ c]=a2()b2c2− − b2c2#⁡ ⁡ ()α α ))− − ab#⁡ ⁡ ()γ γ )()ab#⁡ ⁡ ()γ γ )c2− − ac#⁡ ⁡ ()β β )bc#⁡ ⁡ ()α α ))+ac#⁡ ⁡ ()β β )()ab#⁡ ⁡ ()γ γ )bc#⁡ ⁡ ()α α )− − ac#⁡ ⁡ ()β β )b2)=a2b2c2− − a2b2c2#⁡ ⁡ ()α α )− − a2b2c2#2⁡ ⁡ ()γ γ )+a2b2c2#⁡ ⁡ ()α α )#⁡ ⁡ ()β β )#⁡ ⁡ ()γ γ )+a2b2c2#⁡ ⁡ ()α α )#⁡ ⁡ ()β β )#⁡ ⁡ ()γ γ )− − a2b2c2#⁡ ⁡ ()β β )=a2b2c2()1− − #2⁡ ⁡ ()α α )− − #2⁡ ⁡ ()γ γ )+#⁡ ⁡ ()α α )#⁡ ⁡ ()β β )#⁡ ⁡ ()γ γ )+#⁡ ⁡ ()α α )#⁡ ⁡ ()β β )#⁡ ⁡ ()γ γ )+#2⁡ ⁡ ()β β ))=a2b2c2()1+2#⁡ ⁡ ()α α )#⁡ ⁡ ()β β )#⁡ ⁡ ()γ γ )− − #2⁡ ⁡ ()α α )− − #2⁡ ⁡ ()β β )− − #2⁡ ⁡ ()γ γ )).{displaystyle {begin{aligned}V^{2}left(det Mright)^{2}=det {2}

(Los últimos pasos usan a⋅ ⋅ a=a2{displaystyle mathbf {a} cdot mathbf {a} =a^{2},... a⋅ ⋅ b=ab#⁡ ⁡ γ γ {displaystyle mathbf {a} cdot mathbf {b} =abcos gamma }, a⋅ ⋅ c=ac#⁡ ⁡ β β {displaystyle mathbf {a} cdot mathbf {c} =accos beta }, b⋅ ⋅ c=bc#⁡ ⁡ α α {displaystyle mathbf {b} cdot mathbf {c} =bccos alpha },...)

Correspondiente tetrahedron

El volumen de cualquier tetraedro que comparte tres aristas convergentes de un paralelepípedo es igual a una sexta parte del volumen de ese paralelepípedo (ver prueba).

Superficie

El área de superficie de un paralelepípedo es la suma de las áreas de los paralelogramos delimitadores:

A=2⋅ ⋅ ()Silencioa× × bSilencio+Silencioa× × cSilencio+Silenciob× × cSilencio)=2()abpecado⁡ ⁡ γ γ +bcpecado⁡ ⁡ α α +capecado⁡ ⁡ β β ).{displaystyle {begin{aligned}A paciente=2cdot left(Princemathbf {a} times mathbf {b} Неленыйmathbf {a} times mathbf {c} ¦ times mathbf {c} Silencioderecha)\fr=2left(absin gamma +bcsin alpha +casin beta right).end{aligned}}

Casos especiales por simetría

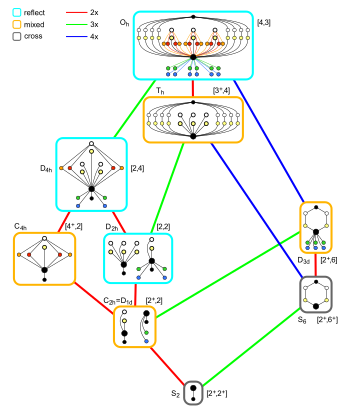Relaciones de subgrupo de simetría octadral con el centro de inversión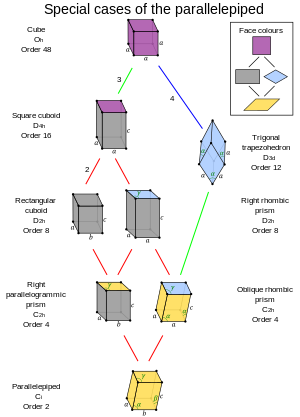

Casos especiales de los paralelos

Formulario	Cube	Cuboide cuadrado	Trigonal trapezohedron	Cuboide rectangular	Derecho prisma rhombic	El prisma paralelogramo derecho	prisma romábico oblicua
Limitaciones	a=b=c{displaystyle a=b=c} α α =β β =γ γ =90∘ ∘ {displaystyle alpha =beta = 'gamma =90^{circ }	a=b{displaystyle a=b} α α =β β =γ γ =90∘ ∘ {displaystyle alpha =beta = 'gamma =90^{circ }	a=b=c{displaystyle a=b=c} α α =β β =γ γ {displaystyle alpha =beta = 'gamma'	α α =β β =γ γ =90∘ ∘ {displaystyle alpha =beta = 'gamma =90^{circ }	a=b{displaystyle a=b} α α =β β =90∘ ∘ {displaystyle alpha =beta =90^{circ }	α α =β β =90∘ ∘ {displaystyle alpha =beta =90^{circ }	a=b{displaystyle a=b} α α =β β {displaystyle alpha =beta }
Simmetría	Oh. Orden 48	D4h Orden 16	D3d Orden 12	D2h Orden 8		C2h Orden 4
Imagen
Caras	6 plazas	2 plazas, 4 rectángulos	6 rhombi	6 rectángulos	4 rectángulos, 2 rhombi	4 rectángulos, 2 paralelogramas	2 rhombi, 4 paralelogramas

• El paralelo con O_h la simetría se conoce como cube, que tiene seis caras cuadradas congruentes.
• El paralelo con D_4h la simetría se conoce como cuboide cuadrado, que tiene dos caras cuadradas y cuatro caras rectangulares congruentes.
• El paralelo con D_3d la simetría se conoce como trigonal trapezohedron, que tiene seis caras rhombic congruentes (también llamada isohedral rhombohedron).
• Para paralelos con D_2h simetría, hay dos casos:
  • Cuboide rectangular: tiene seis caras rectangulares (también llamadas paralelo rectangular, o a veces simplemente un cuboide).
  • Derecho prisma rhombic: tiene dos caras rhombic y cuatro caras rectangulares congruentes.

    Nota: el caso especial totalmente rhombic, con dos caras rhombic y cuatro caras cuadradas congruentes ()a=b=c){displaystyle (a=b=c)}, tiene el mismo nombre, y el mismo grupo de simetría (D_2h orden 8).

• Para paralelos con C_2h simetría, hay dos casos:
  • El prisma paralelogramo derecho: tiene cuatro caras rectangulares y dos caras paralelas.
  • prisma romábico oblicua: tiene dos caras rhombic, mientras que de las otras caras, dos adyacentes son iguales y los otros dos también (los dos pares son la imagen del espejo del otro).

Paralelepípedo perfecto

Un paralelepípedo perfecto es un paralelepípedo con aristas de longitud entera, diagonales de cara y diagonales de espacio. En 2009, se demostró que existen docenas de paralelepípedos perfectos, respondiendo una pregunta abierta de Richard Guy. Un ejemplo tiene las aristas 271, 106 y 103, las diagonales de cara menor 101, 266 y 255, las diagonales de cara mayor 183, 312 y 323 y las diagonales de espacio 374, 300, 278 y 272.

Se conocen algunos paralelepípedos perfectos que tienen dos caras rectangulares. Pero no se sabe si existen con todas las caras rectangulares; tal caso se llamaría un cuboide perfecto.

Paralelotopo

Coxeter llamó a la generalización de un paralelepípedo en dimensiones superiores un paralelotopo. En la literatura moderna, el término paralelepípedo también se usa a menudo en dimensiones más altas (o finitas arbitrarias).

Específicamente en el espacio n-dimensional se llama paralelotopo n-dimensional, o simplemente n-paralelotopo (o n-paralelepípedo). Así, un paralelogramo es un 2-paralelotopo y un paralelepípedo es un 3-paralelotopo.

Más generalmente, un paralelotopo, o paralelotopo voronoi, tiene facetas opuestas paralelas y congruentes. Entonces, un paralelotopo de 2 es un paralelogono que también puede incluir ciertos hexágonos, y un paralelotopo de 3 es un paraleloedro, que incluye 5 tipos de poliedros.

Las diagonales de un paralelotopo n se intersecan en un punto y son bisecadas por este punto. La inversión en este punto deja el paralelotopo n sin cambios. Ver también puntos fijos de grupos de isometría en el espacio euclidiano.

Los bordes que irradian de un vértice de un k-parallelotope forma un k-frame ()v1,...... ,vn){displaystyle (v_{1},ldotsv_{n}} del espacio vectorial, y el paraleloótopo se puede recuperar de estos vectores, tomando combinaciones lineales de los vectores, con pesos entre 0 y 1.

El n- volumen de un n-parallelotope incrustado en Rm{displaystyle mathbb {R} {} {m} Donde m≥ ≥ n{displaystyle mgeq n} se puede computar por medio del determinante Gram. Alternativamente, el volumen es la norma del producto exterior de los vectores:

V=.v1∧ ∧ ⋯ ⋯ ∧ ∧ vn..{displaystyle V=leftantev_{1}wedge cdots wedge v_{n}rightspeda.}

Si m = n, esto equivale al valor absoluto del determinante de n vectores.

Otra fórmula para calcular el volumen de una n-parallelotope P dentro Rn{displaystyle mathbb {R} {} {}} {fn}}, cuyo n + 1 vertices son V0,V1,...... ,Vn{displaystyle V_{0},V_{1},ldotsV_{n}, es

Vol()P)=SilencioDet()[V01]T,[V11]T,...... ,[Vn1]T)Silencio,{fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {f} {fnMicrosoft Sans Serif} {f}fnMicrosoft Sans Serif}

Donde [Vi1]{displaystyle [V_{i} 1] es el vector de fila formado por la concatenación de Vi{displaystyle V_{i} y 1. De hecho, el determinante no cambia si [V01]{displaystyle [V_{0} 1] se restringe de [Vi1]{displaystyle [V_{i} 1] ()i ■ 0), y colocar [V01]{displaystyle [V_{0} 1] en la última posición sólo cambia su signo.

Del mismo modo, el volumen de cualquier n-simplex que comparte n bordes convergentes de un paralelotopo tiene un volumen igual a uno 1/n. del volumen de ese paralelotopo.

Etimología

El término paralelepípedo proviene del griego antiguo παραλληλεπίπεδον (parallēlepípedon, "cuerpo con superficies planas paralelas&# 34;), de parallēl ("parallel") + epípedon ("superficie plana"), de epí- ("sobre") + pedón ("suelo"). Así, las caras de un paralelepípedo son planas y las caras opuestas son paralelas.

En inglés, el término paralelipedón está atestiguado en una traducción de 1570 de los Elementos de Euclides por Henry Billingsley. La ortografía parallelepipedum se utiliza en la edición de 1644 del Cursus mathematicus de Pierre Hérigone. En 1663, el paralelepípedo actual se atestigua en el Chorea gigantum de Walter Charleton.

Charles Hutton's Dictionary (1795) muestra paralelopípedo y paralelopipedón, mostrando la influencia de la forma combinada paralelo-, como si el segundo elemento fuera pipedon en lugar de epipedon. Noah Webster (1806) incluye la ortografía paralelopípedo. La edición de 1989 del Oxford English Dictionary describe parallelopiped (y parallelipiped) explícitamente como formas incorrectas, pero se enumeran sin comentarios en la edición de 2004., y solo pronunciaciones con énfasis en la quinta sílaba pi ( /paɪ/) se dan.