Paralaje
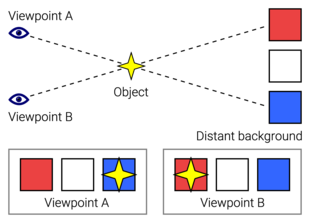
Parallax es un desplazamiento o diferencia en la posición aparente de un objeto visto a lo largo de dos líneas de visión diferentes y se mide por el ángulo o semiángulo de inclinación entre esas dos líneas. Debido al escorzo, los objetos cercanos muestran una paralaje mayor que los objetos más lejanos cuando se observan desde diferentes posiciones, por lo que la paralaje se puede usar para determinar distancias.
Para medir grandes distancias, como la distancia de un planeta o una estrella a la Tierra, los astrónomos utilizan el principio de paralaje. Aquí, el término parallax es el semiángulo de inclinación entre dos líneas de visión hacia la estrella, como se observa cuando la Tierra está en lados opuestos del Sol en su órbita. Estas distancias forman el peldaño más bajo de lo que se llama 'la escala de distancia cósmica', el primero de una sucesión de métodos por los cuales los astrónomos determinan las distancias a los objetos celestes, sirviendo como base para otras mediciones de distancia en astronomía formando los peldaños más altos de la escalera.
El paralaje también afecta a los instrumentos ópticos, como los visores de los rifles, los binoculares, los microscopios y las cámaras réflex de dos lentes que ven los objetos desde ángulos ligeramente diferentes. Muchos animales, junto con los humanos, tienen dos ojos con campos visuales superpuestos que usan paralaje para ganar percepción de profundidad; este proceso se conoce como estereopsis. En la visión por computadora, el efecto se usa para la visión estéreo por computadora, y hay un dispositivo llamado telémetro de paralaje que lo usa para encontrar el rango y, en algunas variaciones, también la altitud a un objetivo.
Un simple ejemplo cotidiano de paralaje se puede ver en los tableros de instrumentos de los vehículos motorizados que utilizan un velocímetro mecánico con forma de aguja. Cuando se ve directamente desde el frente, la velocidad puede mostrar exactamente 60, pero cuando se ve desde el asiento del pasajero, la aguja puede parecer que muestra una velocidad ligeramente diferente debido al ángulo de visión combinado con el desplazamiento de la aguja desde el plano de la dial numérico.
Percepción visual
Como los ojos de los humanos y otros animales están en diferentes posiciones en la cabeza, presentan diferentes vistas simultáneamente. Esta es la base de la estereopsis, el proceso mediante el cual el cerebro aprovecha la paralaje debido a las diferentes vistas del ojo para ganar percepción de profundidad y estimar las distancias a los objetos. Los animales también usan paralaje de movimiento, en el que los animales (o solo la cabeza) se mueven para obtener diferentes puntos de vista. Por ejemplo, las palomas (cuyos ojos no tienen campos de visión superpuestos y, por lo tanto, no pueden usar la estereopsis) mueven la cabeza hacia arriba y hacia abajo para ver la profundidad.
El paralaje de movimiento también se aprovecha en la estereoscopía de movimiento, gráficos por computadora que brindan señales de profundidad a través de la animación de cambio de punto de vista en lugar de la visión binocular.
Astronomía

La paralaje surge debido a un cambio en el punto de vista debido al movimiento del observador, de lo observado o de ambos. Lo esencial es el movimiento relativo. Al observar el paralaje, medir ángulos y usar geometría, se puede determinar la distancia.
Paralaje estelar
La paralaje estelar creada por el movimiento relativo entre la Tierra y una estrella se puede ver, en el modelo copernicano, como surgiendo de la órbita de la Tierra alrededor del Sol: la estrella solo parece moverse en relación con objetos más distantes en el cielo. En un modelo geostático, el movimiento de la estrella debería tomarse como real con la estrella oscilando en el cielo con respecto a las estrellas de fondo.
La paralaje estelar generalmente se mide usando paralaje anual, definida como la diferencia en la posición de una estrella vista desde la Tierra y el Sol, es decir, el ángulo subtendido en una estrella por el radio medio de la La órbita de la Tierra alrededor del Sol. El parsec (3,26 años luz) se define como la distancia para la cual el paralaje anual es de 1 segundo de arco. El paralaje anual normalmente se mide observando la posición de una estrella en diferentes momentos del año a medida que la Tierra se mueve a través de su órbita. La medición del paralaje anual fue la primera forma fiable de determinar las distancias a las estrellas más cercanas. Friedrich Bessel realizó las primeras mediciones exitosas de paralaje estelar en 1838 para la estrella 61 Cygni utilizando un heliómetro. El paralaje estelar sigue siendo el estándar para calibrar otros métodos de medición. Los cálculos precisos de distancia basados en el paralaje estelar requieren una medición de la distancia de la Tierra al Sol, ahora basada en el reflejo del radar en la superficie de los planetas.
Los ángulos involucrados en estos cálculos son muy pequeños y, por lo tanto, difíciles de medir. La estrella más cercana al Sol (y por lo tanto la estrella con el mayor paralaje), Próxima Centauri, tiene un paralaje de 0,7687 ± 0,0003 arcsec. Este ángulo es aproximado al subtendido por un objeto de 2 centímetros de diámetro situado a 5,3 kilómetros de distancia.
El hecho de que el paralaje estelar fuera tan pequeño que no fuera observable en ese momento se usó como el principal argumento científico contra el heliocentrismo durante la edad moderna temprana. Está claro a partir de la geometría de Euclides que el efecto sería indetectable si las estrellas estuvieran lo suficientemente lejos, pero por varias razones, las distancias tan gigantescas involucradas parecían completamente inverosímiles: era una de las principales objeciones de Tycho al heliocentrismo copernicano. que para que sea compatible con la falta de paralaje estelar observable, tendría que haber un vacío enorme e improbable entre la órbita de Saturno (entonces el planeta conocido más lejano) y la octava esfera (las estrellas fijas).
En 1989, el satélite Hipparcos se lanzó principalmente para obtener mejores paralajes y movimientos propios de más de 100 000 estrellas cercanas, aumentando diez veces el alcance del método. Aun así, Hipparcos solo pudo medir los ángulos de paralaje de las estrellas a unos 1.600 años luz de distancia, un poco más del uno por ciento del diámetro de la Vía Láctea. La misión Gaia de la Agencia Espacial Europea, lanzada en diciembre de 2013, puede medir ángulos de paralaje con una precisión de 10 microsegundos de arco, mapeando así estrellas cercanas (y potencialmente planetas) hasta una distancia de decenas de miles de años luz de la Tierra.. En abril de 2014, los astrónomos de la NASA informaron que el telescopio espacial Hubble, mediante el uso de exploración espacial, puede medir con precisión distancias de hasta 10 000 años luz, una mejora diez veces superior a las mediciones anteriores.
Medición de distancia
La medición de distancias por paralaje es un caso especial del principio de triangulación, que establece que uno puede resolver para todos los lados y ángulos en una red de triángulos si, además de todos los ángulos en la red, la longitud de al menos se ha medido al menos un lado. Por lo tanto, la medición cuidadosa de la longitud de una línea de base puede fijar la escala de toda una red de triangulación. En paralaje, el triángulo es extremadamente largo y angosto, y midiendo tanto su lado más corto (el movimiento del observador) como el ángulo superior pequeño (siempre menos de 1 segundo de arco, dejando los otros dos cerca de 90 grados), la longitud de se pueden determinar los lados largos (que en la práctica se consideran iguales).
Asumiendo que el ángulo es pequeño (ver derivación abajo), la distancia a un objeto (medida en parsecs) es la reciprocal del paralax (medido en arcos segundos): Por ejemplo, la distancia a Proxima Centauri es 1/0.7687 = 1.3009 parsecs (4.243 ly).
Paralaje diurno
Paralaje diurno es un paralaje que varía con la rotación de la Tierra o con una diferencia de ubicación en la Tierra. La Luna y, en menor medida, los planetas terrestres o asteroides vistos desde diferentes posiciones de observación en la Tierra (en un momento dado) pueden aparecer colocados de manera diferente contra el fondo de las estrellas fijas.
El paralaje diurno fue utilizado por John Flamsteed en 1672 para medir la distancia a Marte en su oposición y, a través de eso, estimar la unidad astronómica y el tamaño del Sistema Solar.
Paralaje lunar
Paralaje lunar (a menudo abreviatura de paralaje horizontal lunar o paralaje horizontal ecuatorial lunar), es un caso especial de paralaje (diurno): la Luna, siendo el cuerpo celeste más cercano, tiene con mucho la mayor paralaje máxima de cualquier cuerpo celeste, a veces superior a 1 grado.
El diagrama de paralaje estelar también puede ilustrar el paralaje lunar si se reduce la escala del diagrama y se modifica ligeramente. En lugar de 'cerca de la estrella', lea 'Luna', y en lugar de tomar el círculo en la parte inferior del diagrama para representar el tamaño de la órbita de la Tierra alrededor del Sol, tómelo como del tamaño del globo terráqueo y un círculo alrededor de la superficie terrestre. Entonces, el paralaje lunar (horizontal) equivale a la diferencia en la posición angular, en relación con el fondo de estrellas distantes, de la Luna vista desde dos posiciones de visualización diferentes en la Tierra: una de las posiciones de visualización es el lugar desde el cual la Luna se puede ver directamente sobre la cabeza en un momento dado (es decir, se ve a lo largo de la línea vertical en el diagrama); y la otra posición de observación es un lugar desde el cual se puede ver la Luna en el horizonte en el mismo momento (es decir, vista a lo largo de una de las líneas diagonales, desde una posición de la superficie de la Tierra que corresponde aproximadamente a uno de los puntos azules en la diagrama modificado).
La paralaje lunar (horizontal) se puede definir alternativamente como el ángulo subtendido a la distancia de la Luna por el radio de la Tierra, igual al ángulo p en el diagrama cuando se reduce y se modifica como se mencionó anteriormente.
La paralaje horizontal lunar en cualquier momento depende de la distancia lineal de la Luna a la Tierra. La distancia lineal Tierra-Luna varía continuamente a medida que la Luna sigue su órbita perturbada y aproximadamente elíptica alrededor de la Tierra. El rango de la variación en la distancia lineal es de alrededor de 56 a 63,7 radios terrestres, lo que corresponde a una paralaje horizontal de alrededor de un grado de arco, pero que va desde alrededor de 61,4 & # 39; a unos 54'. El Astronomical Almanac y publicaciones similares tabulan la paralaje horizontal lunar y/o la distancia lineal de la Luna a la Tierra en un periódico, p. diariamente para comodidad de los astrónomos (y de los navegantes celestes), y el estudio de cómo varía esta coordenada con el tiempo forma parte de la teoría lunar.
El paralaje también se puede utilizar para determinar la distancia a la Luna.
Una forma de determinar la paralaje lunar desde una ubicación es usando un eclipse lunar. Una sombra completa de la Tierra sobre la Luna tiene un radio aparente de curvatura igual a la diferencia entre los radios aparentes de la Tierra y el Sol vistos desde la Luna. Se puede ver que este radio es igual a 0,75 grados, de lo cual (con el radio solar aparente de 0,25 grados) obtenemos un radio aparente de la Tierra de 1 grado. Esto da como resultado para la distancia Tierra-Luna 60,27 radios terrestres o 384 399 kilómetros (238 854 mi). Este procedimiento fue utilizado por primera vez por Aristarco de Samos e Hiparco, y más tarde llegó a la obra de Ptolomeo. El diagrama de la derecha muestra cómo surge la paralaje lunar diaria en el modelo planetario geocéntrico y geostático en el que la Tierra está en el centro del sistema planetario y no gira. También ilustra el punto importante de que el paralaje no necesita ser causado por ningún movimiento del observador, contrariamente a algunas definiciones de paralaje que dicen que es, pero que puede surgir puramente del movimiento de lo observado.
Otro método consiste en tomar dos fotografías de la Luna al mismo tiempo desde dos lugares de la Tierra y comparar las posiciones de la Luna en relación con las estrellas. Usando la orientación de la Tierra, esas dos medidas de posición y la distancia entre las dos ubicaciones en la Tierra, se puede triangular la distancia a la Luna:
Este es el método al que se refiere Julio Verne en De la Tierra a la Luna:
Hasta entonces, muchas personas no tenían ni idea de cómo se podría calcular la distancia que separa la Luna de la Tierra. La circunstancia fue explotada para enseñarles que esta distancia se obtuvo midiendo el paralaje de la Luna. Si la palabra paralaja apareció para sorprenderlos, se les dijo que era el ángulo subtenido por dos líneas rectas que corren desde ambos extremos del radio de la Tierra hasta la Luna. Si tenían dudas acerca de la perfección de este método, se les mostró inmediatamente que no sólo esta distancia media equivale a un total de doscientos treinta y cuatro mil trescientos cuarenta y siete millas (94.330 leguas) sino también que los astrónomos no estaban en error por más de setenta millas (Entendido 30 leguas).
Paralaje solar
Después de que Copérnico propusiera su sistema heliocéntrico, con la Tierra en revolución alrededor del Sol, fue posible construir un modelo de todo el Sistema Solar sin escala. Para determinar la escala, solo es necesario medir una distancia dentro del Sistema Solar, por ejemplo, la distancia media de la Tierra al Sol (ahora llamada unidad astronómica, o AU). Cuando se encuentra por triangulación, esto se denomina paralaje solar, la diferencia en la posición del Sol visto desde el centro de la Tierra y un punto a un radio de la Tierra, es decir, el ángulo subtendido en el Sol por el radio medio de la Tierra. Conocer la paralaje solar y el radio medio de la Tierra permite calcular la AU, el primer y pequeño paso en el largo camino de establecer el tamaño y la edad de expansión del Universo visible.
Aristarco de Samos ya propuso una forma primitiva de determinar la distancia al Sol en términos de la distancia a la Luna en su libro Sobre los tamaños y distancias del sol y la luna. Observó que el Sol, la Luna y la Tierra forman un triángulo rectángulo (con el ángulo recto en la Luna) en el momento del primer o último cuarto de luna. Luego estimó que el ángulo Luna-Tierra-Sol era de 87°. Usando la geometría correcta pero datos de observación inexactos, Aristarchus concluyó que el Sol estaba un poco menos de 20 veces más lejos que la Luna. El verdadero valor de este ángulo es cercano a los 89° 50', y el Sol está unas 390 veces más lejos. Señaló que la Luna y el Sol tienen tamaños angulares aparentes casi iguales y, por lo tanto, sus diámetros deben ser proporcionales a sus distancias a la Tierra. Por lo tanto, concluyó que el Sol era unas 20 veces más grande que la Luna; esta conclusión, aunque incorrecta, se sigue lógicamente de sus datos incorrectos. Sugiere que el Sol es más grande que la Tierra, lo que podría tomarse para apoyar el modelo heliocéntrico.
Aunque Aristarco' Los resultados fueron incorrectos debido a errores de observación, se basaron en principios geométricos correctos de paralaje y se convirtieron en la base para las estimaciones del tamaño del Sistema Solar durante casi 2000 años, hasta que el tránsito de Venus se observó correctamente en 1761 y 1769. Esto El método fue propuesto por Edmond Halley en 1716, aunque no vivió para ver los resultados. El uso de los tránsitos de Venus tuvo menos éxito de lo que se esperaba debido al efecto de gota negra, pero la estimación resultante, 153 millones de kilómetros, está solo un 2% por encima del valor actualmente aceptado, 149,6 millones de kilómetros.
Mucho más tarde, el Sistema Solar fue "escalado" utilizando el paralaje de los asteroides, algunos de los cuales, como Eros, pasan mucho más cerca de la Tierra que Venus. En una oposición favorable, Eros puede acercarse a la Tierra a 22 milikilómetros de distancia. Durante la oposición de 1900-1901, se lanzó un programa mundial para realizar mediciones de paralaje de Eros para determinar el paralaje solar (o distancia al Sol), con los resultados publicados en 1910 por Arthur Hinks de Cambridge y Charles D. Perrine de la Observatorio Lick, Universidad de California. Perrine publicó informes de progreso en 1906 y 1908. Tomó 965 fotografías con el Crossley Reflector y seleccionó 525 para la medición. Luego, durante un acercamiento más cercano, Harold Spencer Jones llevó a cabo un programa similar en 1930-1931. El valor de la Unidad Astronómica (aproximadamente la distancia Tierra-Sol) obtenido por este programa se consideró definitivo hasta 1968, cuando el radar y los métodos de paralaje dinámico comenzaron a producir mediciones más precisas.
También se han utilizado reflejos de radar, tanto de Venus (1958) como de asteroides, como Ícaro, para determinar el paralaje solar. Hoy, el uso de enlaces de telemetría de naves espaciales ha resuelto este viejo problema. El valor actualmente aceptado de paralaje solar es 8".794 143.
Paralaje de racimo en movimiento
El cúmulo estelar abierto Hyades en Tauro se extiende sobre una parte tan grande del cielo, 20 grados, que los movimientos propios derivados de la astrometría parecen converger con cierta precisión en un punto de perspectiva al norte de Orión. La combinación del movimiento propio aparente (angular) observado en segundos de arco con el movimiento de retroceso verdadero (absoluto) también observado como lo atestigua el corrimiento al rojo Doppler de las líneas espectrales estelares, permite estimar la distancia al cúmulo (151 años luz) y su miembro protagoniza de la misma manera que usa el paralaje anual.
Paralaje dinámico
La paralaje dinámica a veces también se ha utilizado para determinar la distancia a una supernova cuando se ve que el frente de onda óptico del estallido se propaga a través de las nubes de polvo circundantes a una velocidad angular aparente, mientras que se sabe que su verdadera velocidad de propagación es la velocidad de luz.
Derivación
Para un triángulo rectángulo,
Donde es el paralaje, 1 au (149,600,000 km) es aproximadamente la distancia media del Sol a la Tierra, y es la distancia a la estrella. Usando aproximaciones de pequeño ángulo (válidas cuando el ángulo es pequeño en comparación con 1 radio),
entonces el paralaje, medido en segundos de arco, es
Si el paralaje es 1", entonces la distancia es
Esto defines el parsec, una unidad conveniente para medir distancia utilizando paralaje. Por lo tanto, la distancia, medida en parsecs, es simplemente , cuando la paralaja se da en arcseconds.
Error
Las mediciones precisas de paralaje de distancia tienen un error asociado. Este error en el ángulo de paralaje medido no se traduce directamente en un error de distancia, excepto en errores relativamente pequeños. La razón de esto es que un error hacia un ángulo más pequeño da como resultado un error mayor en la distancia que un error hacia un ángulo más grande.
Sin embargo, se puede calcular una aproximación del error de distancia mediante
donde d es la distancia y p es la paralaje. La aproximación es mucho más precisa para errores de paralaje que son pequeños en relación con el paralaje que para errores relativamente grandes. Para obtener resultados significativos en astronomía estelar, el astrónomo holandés Floor van Leeuwen recomienda que el error de paralaje no supere el 10 % del paralaje total al calcular esta estimación de error.
Paralaje espacio-temporal
A partir de sistemas de posicionamiento relativistas mejorados, se ha desarrollado paralaje espacio-temporal generalizando la noción habitual de paralaje en el espacio únicamente. Entonces, los campos de eventos en el espacio-tiempo se pueden deducir directamente sin modelos intermedios de curvatura de la luz por cuerpos masivos como el que se usa en el formalismo PPN, por ejemplo.
Metrología
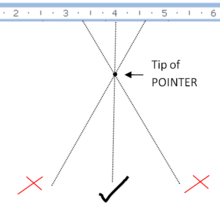
Las mediciones realizadas al ver la posición de algún marcador en relación con algo que se va a medir están sujetas a un error de paralaje si el marcador está a cierta distancia del objeto de medición y no se ve desde la posición correcta. Por ejemplo, si mide la distancia entre dos marcas en una línea con una regla marcada en su superficie superior, el grosor de la regla separará sus marcas de las marcas. Si se ve desde una posición que no es exactamente perpendicular a la regla, la posición aparente cambiará y la lectura será menos precisa de lo que la regla es capaz de hacer.
Ocurre un error similar al leer la posición de un puntero contra una escala en un instrumento como un multímetro analógico. Para ayudar al usuario a evitar este problema, la escala a veces se imprime sobre una franja estrecha de espejo y el ojo del usuario se coloca de modo que el puntero oscurezca su reflejo, lo que garantiza que la línea de visión del usuario sea la correcta. perpendicular al espejo y por lo tanto a la escala. El mismo efecto altera la velocidad leída en el velocímetro de un automóvil por un conductor frente a él y un pasajero a un lado, valores leídos de una retícula, no en contacto real con la pantalla de un osciloscopio, etc.
Fotogrametría
Cuando se ve a través de un visor estéreo, el par de imágenes aéreas ofrece un efecto estéreo pronunciado de paisajes y edificios. Los edificios altos parecen "desplomarse" en la dirección que se aleja del centro de la fotografía. Las mediciones de este paralaje se utilizan para deducir la altura de los edificios, siempre que se conozcan la altura de vuelo y las distancias de referencia. Este es un componente clave del proceso de fotogrametría.
Fotografía
El error de paralaje se puede ver al tomar fotos con muchos tipos de cámaras, como las cámaras réflex de doble lente y las que incluyen visores (como las cámaras con telémetro). En tales cámaras, el ojo ve al sujeto a través de una óptica diferente (el visor o una segunda lente) que aquella a través de la cual se toma la foto. Como el visor a menudo se encuentra sobre la lente de la cámara, las fotos con error de paralaje a menudo son ligeramente más bajas de lo previsto, siendo el ejemplo clásico la imagen de una persona con la cabeza recortada. Este problema se soluciona en las cámaras réflex de lente única, en las que el visor ve a través de la misma lente a través de la cual se toma la foto (con la ayuda de un espejo móvil), evitando así el error de paralaje.
El paralaje también es un problema en la unión de imágenes, como las panorámicas.
Miras de armas
El paralaje afecta a los dispositivos de mira de las armas a distancia de muchas formas. En las miras instaladas en armas pequeñas y arcos, etc., la distancia perpendicular entre la mira y el eje de lanzamiento del arma (por ejemplo, el eje del cañón de un arma), generalmente conocida como "altura de la mira "—puede inducir errores significativos al apuntar cuando se dispara a corta distancia, particularmente cuando se dispara a objetivos pequeños. Este error de paralaje se compensa (cuando es necesario) a través de cálculos que también toman en cuenta otras variables como la caída de la bala, el viento y la distancia a la que se espera que esté el objetivo. La altura de la vista se puede usar para sacar ventaja cuando se "mira hacia adentro" rifles para uso en el campo. Un rifle de caza típico (.222 con mira telescópica) apuntado a 75 m seguirá siendo útil de 50 a 200 m (55 a 219 yd) sin necesidad de ajustes adicionales.
Miras ópticas
En algunos instrumentos ópticos reticulados, como telescopios, microscopios o miras telescópicas ("visores") utilizados en armas pequeñas y teodolitos, el paralaje puede crear problemas cuando la retícula no coincide con el plano focal del imagen de destino Esto se debe a que cuando la retícula y el objetivo no están en el mismo foco, las distancias correspondientes ópticamente que se proyectan a través del ocular también son diferentes, y el ojo del usuario registrará la diferencia de paralaje entre la retícula y el objetivo (cada vez que cambia la posición de los ojos) como un desplazamiento relativo uno encima del otro. El término cambio de paralaje se refiere a la aparente "flotación" movimientos de la retícula sobre la imagen objetivo cuando el usuario mueve su cabeza/ojo lateralmente (arriba/abajo o izquierda/derecha) detrás de la mira, es decir, un error donde la retícula no permanece alineada con la óptica del usuario eje.
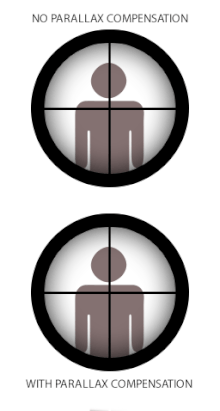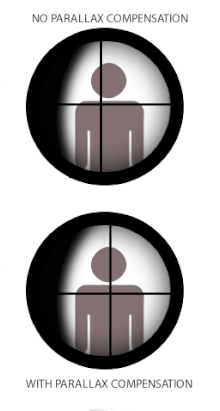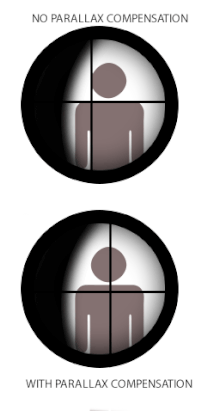
Algunos visores de armas de fuego están equipados con un mecanismo de compensación de paralaje, que consta de un elemento óptico móvil que permite que el sistema óptico cambie el enfoque de la imagen objetivo a distancias variables en el mismo plano óptico de la retícula (o viceversa). Es posible que muchas miras telescópicas de bajo nivel no tengan compensación de paralaje porque en la práctica aún pueden funcionar de manera muy aceptable sin eliminar el cambio de paralaje. En este caso, el alcance a menudo se establece fijo en una distancia libre de paralaje designada que mejor se adapte a su uso previsto. Las distancias libres de paralaje estándar típicas de fábrica para visores de caza son 100 yd (o 90 m) para que sean adecuados para tiros de caza que rara vez superan las 300 yd/m. Algunos visores de estilo militar y de competición sin compensación de paralaje se pueden ajustar para que estén libres de paralaje en rangos de hasta 300 yardas/m para que sean más adecuados para apuntar a rangos más largos. Los visores para armas con rangos prácticos más cortos, como pistolas de aire comprimido, rifles de percusión anular, escopetas y armas de avancarga, tendrán configuraciones de paralaje para distancias más cortas, comúnmente 50 m (55 yd) para visores de percusión anular y 100 m (110 yd) para escopetas y armas de avancarga. Los visores de las pistolas de aire se encuentran muy a menudo con paralaje ajustable, generalmente en forma de un diseño de objetivo ajustable (o 'AO' para abreviar), y pueden ajustarse hasta 3 metros (3,3 yd).
Reflector sin aumento o "reflex" las miras pueden ser teóricamente "libres de paralaje". Pero dado que estas miras usan luz colimada paralela, esto solo es cierto cuando el objetivo está en el infinito. A distancias finitas, el movimiento del ojo perpendicular al dispositivo provocará un movimiento de paralaje en la imagen del retículo en relación exacta con la posición del ojo en la columna cilíndrica de luz creada por la óptica colimadora. Las miras de armas de fuego, como algunas miras de punto rojo, intentan corregir esto al no enfocar la retícula al infinito, sino a una distancia finita, un rango objetivo diseñado donde la retícula mostrará muy poco movimiento debido al paralaje. Algunos fabricantes comercializan modelos de visores reflectores a los que denominan "sin paralaje" pero esto se refiere a un sistema óptico que compensa la aberración esférica fuera del eje, un error óptico inducido por el espejo esférico utilizado en la mira que puede causar que la posición de la retícula se desvíe del eje óptico de la mira con el cambio en la posición del ojo.
Disparos de artillería
Debido al posicionamiento de los cañones de artillería naval o de campo, cada uno tiene una perspectiva ligeramente diferente del objetivo en relación con la ubicación del propio sistema de control de fuego. Por lo tanto, al apuntar sus armas al objetivo, el sistema de control de fuego debe compensar el paralaje para asegurar que el fuego de cada arma converja en el objetivo.
Telémetros
Se puede usar un telémetro de coincidencia o un telémetro de paralaje para encontrar la distancia a un objetivo.
Arte
Varias de las obras escultóricas de Mark Renn juegan con el paralaje y parecen abstractas hasta que se ven desde un ángulo específico. Una de esas esculturas es La puerta de Darwin (en la foto) en Shrewsbury, Inglaterra, que desde cierto ángulo parece formar una cúpula, según Historic England, en "la forma de un casco sajón con una ventana normanda... inspirada en las características de la iglesia de Santa María a la que asistió Charles Darwin cuando era niño.
Como metáfora
En un sentido filosófico/geométrico: un cambio aparente en la dirección de un objeto, causado por un cambio en la posición de observación que proporciona una nueva línea de visión. El desplazamiento aparente, o diferencia de posición, de un objeto, visto desde dos estaciones o puntos de vista diferentes. En la escritura contemporánea, el paralaje también puede ser la misma historia, o una historia similar de aproximadamente la misma línea de tiempo, de un libro, contada desde una perspectiva diferente en otro libro. La palabra y el concepto ocupan un lugar destacado en la novela de James Joyce de 1922, Ulysses. Orson Scott Card también usó el término al referirse a la Sombra de Ender en comparación con el Juego de Ender.
La metáfora es invocada por el filósofo esloveno Slavoj Žižek en su libro de 2006 The Parallax View, tomando prestado el concepto de "vista de paralaje" del filósofo y crítico literario japonés Kojin Karatani. Žižek señala,
El giro filosófico a añadir (parallax), por supuesto, es que la distancia observada no es simplemente subjetiva, ya que el mismo objeto que existe 'fuera se ve desde dos posturas o puntos de vista diferentes. Es más bien que, como lo habría dicho Hegel, el sujeto y el objeto están inherentemente mediados de modo que un cambio "epistemológico" en el punto de vista del sujeto siempre refleja un cambio ontológico en el objeto mismo. O, ponerlo en Lacaneso, la mirada del sujeto siempre está inscrita en el objeto percibido en sí, bajo el pretexto de su "punto ciego", que está "en el objeto más que el objeto mismo, el punto desde el que el objeto mismo devuelve la mirada. Claro que la foto está en mi ojo, pero también estoy en la foto.
—Slavoj Žižek, La vista Parallax
Contenido relacionado
Enana marrón
Ley de Titius-Bode
Apolo 10