Paradoja de faraday

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Paradoja aparente con la ley de inducción de Faraday

El Faraday paradox o Paradoja de Faraday es cualquier experimento en el que la ley de Michael Faraday de la inducción electromagnética parece predecir un resultado incorrecto. Las paradojas caen en dos clases:

La ley de Faraday parece predecir que habrá cero fuerza electromotiva (EMF) pero hay un EMF no cero.
La ley de Faraday parece predecir que habrá un EMF no cero, pero hay cero EMF.

Faraday dedujo su ley de inducción en 1831, después de inventar el primer generador electromagnético o dinamo, pero nunca estuvo satisfecho con su propia explicación de la paradoja.

Ley de Faraday comparada con la ecuación de Maxwell-Faraday

Ley de Faraday (también conocida como Faraday-Lenz law) afirma que la fuerza electromotiva (EMF) es dada por el derivado total del flujo magnético con respecto al tiempo t:

{displaystyle {mathcal {E}}=-{frac {dPhi _{B}}{dt}},}

Donde ${displaystyle {mathcal {E}}}$ es el EMF y ⋅_B es el flujo magnético a través de un bucle de alambre. La dirección de la fuerza electromotiva es dada por la ley de Lenz. Un hecho a menudo pasado por alto es que la ley de Faraday se basa en el derivado total, no el derivado parcial, del flujo magnético. Esto significa que un EMF puede ser generado incluso si el flujo total a través de la superficie es constante. Para superar este problema, se pueden utilizar técnicas especiales. Vea a continuación la sección sobre el uso de técnicas especiales con la ley de Faraday.

Sin embargo, la interpretación más común de la ley de Faraday es que:

La fuerza electromotiva inducida en cualquier circuito cerrado es igual a la negativa de la velocidad de cambio del flujo magnético encerrado por el circuito.

Esta versión de la ley de Faraday se mantiene estrictamente sólo cuando el circuito cerrado es un bucle de alambre infinitamente delgado, y es inválido en otras circunstancias. Se ignora el hecho de que la ley de Faraday está definida por el total, no parcial, derivado del flujo magnético y también el hecho de que EMF no está necesariamente confinado a un camino cerrado, pero también puede tener componentes radiales como se discute a continuación. Una versión diferente, la ecuación Maxwell-Faraday (discutida abajo), es válida en todas las circunstancias, y cuando se utiliza junto con la ley de fuerza Lorentz es consistente con la aplicación correcta de la ley de Faraday.

Esbozo de la prueba de la ley de Faraday de las ecuaciones de Maxwell y la ley de fuerza de Lorentz.

Considere el tiempo-derivativo del flujo a través de un bucle posiblemente en movimiento, con área ${displaystyle Sigma (t)}$ :

{displaystyle {frac {dPhi _{B}}{dt}}={frac {d}{dt}}int _{Sigma (t)}mathbf {B} (t)cdot dmathbf {A} }

La integral puede cambiar con el tiempo por dos razones: El integrado puede cambiar, o la región de integración puede cambiar. Por lo tanto, éstos agregan linealmente:

{displaystyle left.{frac {dPhi _{B}}{dt}}right|_{t=t_{0}}=left(int _{Sigma (t_{0})}left.{frac {partial mathbf {B} }{partial t}}right|_{t=t_{0}}cdot dmathbf {A} right)+left({frac {d}{dt}}int _{Sigma (t)}mathbf {B} (t_{0})cdot dmathbf {A} right)}

Donde t₀ es un tiempo fijo dado. Demostraremos que el primer término en el lado derecho corresponde al transformador EMF, el segundo al movimiento EMF. El primer término en el lado derecho puede ser reescrito utilizando la forma integral de la ecuación Maxwell-Faraday:

{displaystyle int _{Sigma (t_{0})}left.{frac {partial mathbf {B} }{partial t}}right|_{t=t_{0}}cdot dmathbf {A} =-oint _{partial Sigma (t_{0})}mathbf {E} (t_{0})cdot d{boldsymbol {ell }}}

A continuación, analizamos el segundo término en el lado derecho:

{displaystyle {frac {d}{dt}}int _{Sigma (t)}mathbf {B} (t_{0})cdot dmathbf {A} }

Esta es la parte más difícil de la prueba; más detalles y enfoques alternativos se pueden encontrar en referencias. A medida que el bucle se mueve y/o deforma, barre una superficie (ver figura a la derecha). El flujo magnético a través de esta superficie de barrido corresponde al flujo magnético que está entrando o saliendo del bucle, y por lo tanto este es el flujo magnético que contribuye al tiempo-derivativo. (Este paso utiliza implícitamente la ley de Gauss para el magnetismo: Como las líneas de flujo no tienen principio ni fin, sólo pueden entrar en el bucle al cortar por el alambre.) Como una pequeña parte del bucle ${displaystyle d{boldsymbol {ell }}}$ movimientos con velocidad v por un corto tiempo ${displaystyle dt}$ , que barre un vector de área vectorial ${displaystyle dmathbf {A} =mathbf {v} ,dttimes d{boldsymbol {ell }}}$ . Por lo tanto, el cambio en el flujo magnético a través del bucle aquí es

{displaystyle mathbf {B} cdot (mathbf {v} ,dttimes d{boldsymbol {ell }})=-dt,d{boldsymbol {ell }}cdot (mathbf {v} times mathbf {B})}

Por lo tanto:

{displaystyle {frac {d}{dt}}int _{Sigma (t)}mathbf {B} (t_{0})cdot dmathbf {A} =-oint _{partial Sigma (t_{0})}(mathbf {v} (t_{0})times mathbf {B} (t_{0}))cdot d{boldsymbol {ell }}}

Donde v es la velocidad de un punto en el bucle ${displaystyle partial Sigma }$ .

Ponerlos juntos,

{displaystyle left.{frac {dPhi _{B}}{dt}}right|_{t=t_{0}}=left(-oint _{partial Sigma (t_{0})}mathbf {E} (t_{0})cdot d{boldsymbol {ell }}right)+left(-oint _{partial Sigma (t_{0})}(mathbf {v} (t_{0})times mathbf {B} (t_{0}))cdot d{boldsymbol {ell }}right)}

Mientras tanto, EMF se define como la energía disponible por carga de unidad que viaja una vez alrededor del bucle de alambre. Por lo tanto, por la ley de la fuerza Lorentz,

{displaystyle mathrm {EMF} =oint left(mathbf {E} +mathbf {v} times mathbf {B} right)cdot {text{d}}{boldsymbol {ell }}}

Combinando estos, ${displaystyle {frac {dPhi _{B}}{dt}}=-mathrm {EMF} }$

La ecuación de Maxwell-Faraday es una generalización de la ley de Faraday que establece que un campo magnético variable en el tiempo siempre va acompañado de un campo eléctrico no conservativo que varía espacialmente, y viceversa. La ecuación de Maxwell-Faraday es:

${displaystyle nabla times mathbf {E} =-{frac {partial mathbf {B} }{partial t}}}$

(en unidades SI) donde ${displaystyle partial }$ es el operador derivado parcial, ${displaystyle nabla times }$ es el operador del rizo y otra vez E()r, t) es el campo eléctrico y B()r, t) es el campo magnético. Estos campos generalmente pueden ser funciones de posición r y tiempo t.

La ecuación Maxwell-Faraday es una de las cuatro ecuaciones de Maxwell, y por lo tanto juega un papel fundamental en la teoría del electromagnetismo clásico. También se puede escribir en un Forma integral por el teorema Kelvin-Stokes.

Paradojas en las que la ley de inducción de Faraday parece predecir cero EMF pero en realidad predice no cero EMF

Estas paradojas generalmente se resuelven por el hecho de que un EMF puede ser creado por un flujo cambiante en un circuito como se explica en la ley de Faraday o por el movimiento de un conductor en un campo magnético. Feynman explica esto como se indica a continuación. Véase también A. Sommerfeld, Volumen III Electrodinámica Academic Press, página 362.

El equipo

El experimento requiere algunos componentes simples (ver Figura 1): un imán cilíndrico, un disco conductor con un borde conductor, un eje conductor, algo de cableado y un galvanómetro. El disco y el imán están montados a poca distancia entre sí sobre el eje, sobre el cual pueden girar libremente alrededor de sus propios ejes de simetría. Un circuito eléctrico se forma conectando contactos deslizantes: uno al eje del disco y el otro a su borde. Se puede insertar un galvanómetro en el circuito para medir la corriente.

El procedimiento

El experimento se desarrolla en tres pasos:

El imán se mantiene para evitar que gire, mientras que el disco se lanza sobre su eje. El resultado es que el galvanometer registra una corriente directa. Por lo tanto, el aparato actúa como generador, llamado el generador Faraday, el disco Faraday o el generador homopolar (o unipolar).
El disco se mantiene estacionario mientras el imán se lanza sobre su eje. El resultado es que el galvanometer no registra corriente.
El disco y el imán se juntan. El galvanometer registra una corriente, como lo hizo en el paso 1.

¿Por qué es esto paradójico?

El experimento es descrito por algunos como una "paradoja" ya que parece, a primera vista, violar la ley de Faraday de la inducción electromagnética, porque el flujo a través del disco parece ser el mismo sin importar lo que esté girando. Por lo tanto, se prevé que el EMF es cero en los tres casos de rotación. La discusión a continuación muestra este punto de vista se deriva de una opción incorrecta de superficie sobre la cual calcular el flujo.

La paradoja parece un poco diferente desde el punto de vista de las líneas de flujo: en el modelo de inducción electromagnética de Faraday, un campo magnético consistía en líneas imaginarias de flujo magnético, similares a las líneas que aparecen cuando se esparcen limaduras de hierro sobre papel y sostenido cerca de un imán. Se propone que la FEM sea proporcional a la tasa de corte de las líneas de flujo. Si se imagina que las líneas de flujo se originan en el imán, entonces estarían estacionarias en el marco del imán, y al girar el disco con respecto al imán, ya sea girando el imán o el disco, debería producirse una FEM, pero al girar ambos juntos no deberían hacerlo.

La explicación de Faraday

En el modelo de inducción electromagnética de Faraday, un circuito recibía una corriente inducida cuando cortaba líneas de flujo magnético. Según este modelo, el disco de Faraday debería haber funcionado cuando se hacía girar el disco o el imán, pero no ambos. Faraday intentó explicar el desacuerdo con la observación asumiendo que el campo del imán, completo con sus líneas de flujo, permanecía estacionario mientras el imán giraba (una imagen completamente precisa, pero tal vez no intuitiva en el modelo de líneas de flujo). ). En otras palabras, las líneas de flujo tienen su propio marco de referencia. Como se muestra en la siguiente sección, la física moderna (desde el descubrimiento del electrón) no necesita la imagen de las líneas de flujo y disipa la paradoja.

Explicaciones modernas

Un circuito no es necesariamente un bucle

En el paso 1, la paradoja se puede resolver fácilmente: el circuito no constituye un simple bucle de cable, como lo postula la ley de inducción de Faraday; es más bien la unión de dos bucles, porque la corriente puede fluir a través de las dos mitades del borde (ver figura 2). Si, por el contrario, se conserva sólo una parte de la llanta desde la unión del radio hasta el cepillo, entonces todo el circuito es ahora un verdadero bucle cuya forma varía con el tiempo; entonces se aplica la ley de Faraday y conduce a resultados correctos.

Teniendo en cuenta el camino de regreso

En el paso 2, dado que no se observa corriente, se podría concluir que el campo magnético no giró con el imán giratorio. (Ya sea que lo haga o no de manera efectiva o relativa, la fuerza de Lorentz es cero ya que v es cero en relación con el marco del laboratorio. Por lo tanto, no se mide la corriente desde el marco del laboratorio). El uso de la ecuación de Lorentz Explicar esta paradoja ha dado lugar a un debate en la literatura sobre si un campo magnético gira o no con un imán. Dado que la fuerza sobre las cargas expresada por la ecuación de Lorentz depende del movimiento relativo del campo magnético (es decir, el marco del laboratorio) con respecto al conductor donde se encuentra el EMF, se especuló que en el caso en que el imán gira con el disco, pero un voltaje todavía se desarrolla, el campo magnético (es decir, el marco del laboratorio) no debe girar con el material magnético (por supuesto, ya que es el marco del laboratorio), mientras que la definición efectiva del marco del campo magnético o la "rotación efectiva/relativa del el campo" gira sin movimiento relativo con respecto al disco conductor.

Una reflexión cuidadosa demostró que, si se suponía que el campo magnético giraba con el imán y el imán giraba con el disco, todavía se debería producir una corriente, no por EMF en el disco (no hay movimiento relativo entre el disco y el imán) sino en el circuito externo que une las escobillas, que de hecho está en movimiento relativo con respecto al imán giratorio. (Los cepillos están en el marco del laboratorio).

Este mecanismo concuerda con las observaciones relacionadas con las rutas de retorno: se genera un EMF cada vez que el disco se mueve en relación con la ruta de retorno, independientemente de la rotación del imán. De hecho, se demostró que mientras se utilice un bucle de corriente para medir los campos electromagnéticos inducidos por el movimiento del disco y el imán, no es posible saber si el campo magnético gira o no con el imán. (Esto depende de la definición, el movimiento de un campo solo se puede definir de manera efectiva/relativa. Si sostiene que el flujo de campo es una entidad física, gira o depende de cómo se genera. Pero esto no altera (lo que se usa en la fórmula de Lorentz, especialmente la v, la velocidad del portador de carga relativa al marco donde se realiza la medición y la intensidad del campo varía según la relatividad en cualquier punto del espacio-tiempo).

Se han propuesto varios experimentos utilizando mediciones electrostáticas o haces de electrones para resolver el problema, pero aparentemente ninguno se ha realizado con éxito hasta la fecha.

Usando la fuerza de Lorentz

La fuerza F actuando en una partícula de carga eléctrica q con velocidad instantánea v, debido a un campo eléctrico externo E y campo magnético B, es dada por la fuerza Lorentz:

${displaystyle mathbf {F} =q(mathbf {E} +mathbf {v} times mathbf {B})}$

donde × es el producto cruzado del vector. Todas las cantidades en negrita son vectores. El campo eléctrico relativistamente correcto de una carga puntual varía con la velocidad como:

{displaystyle mathbf {E} ={frac {q}{4pi epsilon _{0}}}{frac {1-v^{2}/c^{2}}{(1-v^{2}sin ^{2}theta /c^{2})^{3/2}}}{frac {mathbf {{hat {r}}'} }{|mathbf {r} '|^{2}}}}

Donde ${displaystyle mathbf {hat {r}} '}$ es el vector unitario apuntando desde la posición actual (no retrotraída) de la partícula hasta el punto en que se está midiendo el campo, y θ es el ángulo entre ${displaystyle mathbf {v} }$ y ${displaystyle mathbf {r} '}$ . El campo magnético B de un cargo es:

{displaystyle mathbf {B} ={frac {1}{c^{2}}}mathbf {v} times mathbf {E} }

En el nivel más subyacente, la fuerza total de Lorentz es el resultado acumulativo de los campos eléctricos E y los campos magnéticos B de cada carga que actúa sobre todas las demás cargas.

Cuando el imán gira, pero las líneas de flujo están estacionarias y el conductor está estacionario

Considere el caso especial en el que el disco conductor cilíndrico está estacionario pero el disco magnético cilíndrico está girando. En tal situación, la velocidad media v de las cargas en el disco conductor es inicialmente cero y, por lo tanto, la fuerza magnética F = qv × B es 0, donde v es la velocidad media de una carga q del circuito con respecto al marco donde se toman las medidas, y q es la carga de un electrón.

Cuando el imán y las líneas de flujo están estacionarios y el conductor está girando

Después del descubrimiento del electrón y las fuerzas que lo afectan, se hizo posible una resolución microscópica de la paradoja. Consulte la Figura 1. Las partes metálicas del aparato son conductoras y confinan una corriente debida al movimiento electrónico dentro de los límites metálicos. Todos los electrones que se mueven en un campo magnético experimentan una fuerza de Lorentz de F = qv × B, donde v es la velocidad de los electrones en relación con el marco donde se toman las mediciones, y q es la carga de un electrón. Recuerde, no existe un marco llamado "marco del campo electromagnético". Un marco se establece en un punto espacio-temporal específico, no en un campo extendido o una línea de flujo como un objeto matemático. Es una cuestión diferente si considera el flujo como una entidad física (ver Cuántico de flujo magnético), o considera la definición efectiva/relativa de movimiento/rotación de un campo (ver más abajo). Esta nota ayuda a resolver la paradoja.

La fuerza de Lorentz es perpendicular tanto a la velocidad de los electrones, que está en el plano del disco, como al campo magnético, que es normal (superficie normal) al disco. Un electrón en reposo en el marco del disco se mueve circularmente con el disco en relación con el campo B (es decir, el eje de rotación o el marco del laboratorio, recuerde la nota anterior) y, por lo tanto, experimenta una fuerza radial de Lorentz. En la Figura 1, esta fuerza (sobre una carga positiva, no sobre un electrón) se dirige hacia el borde según la regla de la mano derecha.

Por supuesto, esta fuerza radial, que es la causa de la corriente, crea un componente radial de la velocidad del electrón, generando a su vez su propio componente de fuerza de Lorentz que se opone al movimiento circular de los electrones, tendiendo a ralentizar el disco. ;s rotación, pero los electrones retienen un componente de movimiento circular que continúa impulsando la corriente a través de la fuerza radial de Lorentz.

Uso de técnicas especiales con la ley de Faraday

El flujo a través de la parte del camino desde el cepillo hasta el borde, a través del bucle exterior y el eje hasta el centro del disco es siempre cero porque el campo magnético está en el plano de este camino (no perpendicular a él). ), no importa qué esté girando, por lo que la fem integrada alrededor de esta parte de la trayectoria es siempre cero. Por lo tanto, la atención se centra en la parte del recorrido desde el eje a través del disco hasta el cepillo en la llanta.

La ley de inducción de Faraday se puede expresar en palabras como:

La fuerza electromotiva inducida o EMF en cualquier circuito cerrado es igual a la velocidad de cambio del flujo magnético a través del circuito.

Matemáticamente, la ley se establece:

{displaystyle {mathcal {E}}=-{frac {dPhi _{B}}{dt}}=-{frac {d}{dt}}iint _{Sigma (t)}dmathbf {A} cdot mathbf {B} (mathbf {r} t)}

donde Φ_B es el flujo y dA es un elemento vectorial del área de una superficie en movimiento Σ(t) delimitado por el bucle alrededor del cual se encuentra la FEM.

¿Cómo se puede conectar esta ley con el generador de discos de Faraday, donde el enlace de flujo parece ser simplemente el campo B multiplicado por el área del disco?

Un enfoque consiste en definir la noción de "tasa de cambio de vinculación de flujo" dibujando una línea hipotética a través del disco desde el cepillo hasta el eje y preguntando cuánto enlace de flujo pasa por esta línea por unidad de tiempo. Consulte la Figura 2. Suponiendo un radio R para el disco, un sector del disco con ángulo central θ tiene un área:

{displaystyle A={frac {theta }{2pi }}pi R^{2}}

entonces la velocidad con la que el flujo pasa por la línea imaginaria es

{displaystyle {mathcal {E}}=-{frac {dPhi _{B}}{dt}}=B{frac {dA}{dt}}=B {frac {R^{2}}{2}} {frac {dtheta }{dt}}=B {frac {R^{2}}{2}}omega }

con ω = dθ / dt la velocidad angular de rotación. El signo se elige basándose en la ley de Lenz: el campo generado por el movimiento debe oponerse al cambio de flujo causado por la rotación. Por ejemplo, el circuito con el segmento radial en la Figura 2 según la regla de la mano derecha se suma al campo B aplicado, tendiendo a aumentar el enlace de flujo. Eso sugiere que el flujo a través de este camino está disminuyendo debido a la rotación, por lo que dθ / dt es negativo.

Este resultado de corte de flujo para EMF se puede comparar con el cálculo del trabajo realizado por unidad de carga haciendo que una carga de prueba infinitesimal atraviese la línea hipotética usando la fuerza de Lorentz / carga unitaria en el radio r, es decir | v × B| = Bv = Brω:

{displaystyle {mathcal {E}}=int _{0}^{R}drBromega ={frac {R^{2}}{2}}Bomega }

que es el mismo resultado.

La metodología anterior para encontrar el flujo cortado por el circuito se formaliza en la ley de flujo al tratar adecuadamente la derivada del tiempo de la superficie delimitadora Σ(t). Por supuesto, la derivada temporal de una integral con límites dependientes del tiempo no es simplemente la derivada temporal del integrando solo, un punto que a menudo se olvida; ver regla integral de Leibniz y fuerza de Lorentz.

Al elegir la superficie Σ(t), las restricciones son que (i) tiene que estar delimitada por una curva cerrada alrededor de la cual se debe encontrar la FEM, y (ii) tiene para capturar el movimiento relativo de todas las partes móviles del circuito. Enfáticamente no se requiere que la curva delimitadora corresponda a una línea física de flujo de la corriente. Por otro lado, la inducción tiene que ver con el movimiento relativo, y el camino debe capturar enfáticamente cualquier movimiento relativo. En un caso como el de la Figura 1, donde una parte de la ruta actual se distribuye en una región en el espacio, el EMF que impulsa la corriente se puede encontrar utilizando una variedad de rutas. La figura 2 muestra dos posibilidades. Todos los caminos incluyen el obvio bucle de retorno, pero en el disco se muestran dos caminos: uno es un camino geométricamente simple, el otro es tortuoso. Somos libres de elegir el camino que queramos, pero una parte de cualquier camino aceptable está fijado en el propio disco y gira con el disco. El flujo se calcula a lo largo de toda la ruta, el bucle de retorno más el segmento del disco y se encuentra su tasa de cambio.

En este ejemplo, todos estos caminos conducen a la misma tasa de cambio de flujo y, por lo tanto, al mismo EMF. Para dar una idea acerca de esta independencia de trayectoria, en la Figura 3 el disco de Faraday está desenvuelto en una tira, haciéndolo parecerse a un problema de rectángulo deslizante. En el caso del rectángulo deslizante, resulta obvio que el patrón de flujo de corriente dentro del rectángulo es independiente del tiempo y, por lo tanto, irrelevante para la tasa de cambio del flujo que une el circuito. No es necesario considerar exactamente cómo la corriente atraviesa el rectángulo (o el disco). Cualquier elección de trayectoria que conecte la parte superior e inferior del rectángulo (del eje al cepillo en el disco) y que se mueva con el rectángulo (girando con el disco) barre la misma tasa de cambio de flujo y predice la misma EMF. . Para el disco, esta tasa de cambio de estimación de flujo es la misma que la realizada anteriormente basándose en la rotación del disco más allá de una línea que une el cepillo con el eje.

Configuración con ruta de retorno

Si el imán se está "moviendo" es irrelevante en este análisis, debido al flujo inducido en el camino de retorno. El movimiento relativo crucial es el del disco y el camino de retorno, no el del disco y el imán. Esto queda más claro si se utiliza un disco de Faraday modificado en el que la ruta de retorno no es un cable sino otro disco. Es decir, monte dos discos conductores uno al lado del otro en el mismo eje y déjelos tener contacto eléctrico deslizante en el centro y en la circunferencia. La corriente será proporcional a la rotación relativa de los dos discos e independiente de cualquier rotación del imán.

Configuración sin camino de retorno

Un disco de Faraday también puede funcionar sin galvanómetro ni recorrido de retorno. Cuando el disco gira, los electrones se acumulan a lo largo del borde y dejan un déficit cerca del eje (o al revés). En principio, es posible medir la distribución de carga, por ejemplo, a través de la fuerza electromotriz generada entre la llanta y el eje (aunque no necesariamente es fácil). Esta separación de carga será proporcional a la velocidad de rotación relativa entre el disco y el imán.

Paradojas en las que la ley de inducción de Faraday parece predecir campos electromagnéticos distintos de cero, pero en realidad predice campos electromagnéticos cero

Estas paradojas generalmente se resuelven determinando que el movimiento aparente del circuito es en realidad una deconstrucción del circuito seguida de una reconstrucción del circuito en un camino diferente.

Una regla adicional

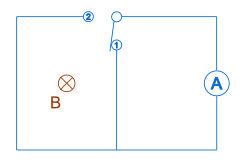
En el caso en que el disco gira solo, no hay cambio en el flujo a través del circuito; sin embargo, hay una fuerza electromotriz inducida contrariamente a la ley de Faraday. También podemos mostrar un ejemplo cuando hay un cambio en el flujo, pero no hay voltaje inducido. La Figura 5 (cerca de la derecha) muestra la configuración utilizada en el experimento de Tilley. Es un circuito con dos bucles o mallas. Hay un galvanómetro conectado en el bucle derecho, un imán en el centro del bucle izquierdo, un interruptor en el bucle izquierdo y un interruptor entre los bucles. Empezamos con el interruptor de la izquierda abierto y el de la derecha cerrado. Cuando el interruptor de la izquierda está cerrado y el interruptor de la derecha está abierto, no hay cambio en el campo del imán, pero sí en el área del circuito del galvanómetro. Esto significa que hay un cambio en el flujo. Sin embargo, el galvanómetro no se desvió, lo que significa que no hubo voltaje inducido y la ley de Faraday no funciona en este caso. Según A. G. Kelly, esto sugiere que un voltaje inducido en el experimento de Faraday se debe al "corte" del circuito por las líneas de flujo, y no por "enlace de flujo" o el cambio real en el flujo. Esto se desprende del experimento de Tilley porque no hay movimiento de las líneas de fuerza a través del circuito y, por lo tanto, no hay corriente inducida aunque haya un cambio en el flujo a través del circuito. Nussbaum sugiere que para que la ley de Faraday sea válida, se debe trabajar para producir el cambio en el flujo.
Para comprender esta idea, analizaremos el argumento dado por Nussbaum. Comenzamos calculando la fuerza entre dos cables portadores de corriente. La fuerza sobre el alambre 1 debida al alambre 2 está dada por:

{displaystyle mathbf {F} _{21}={frac {mu _{0}}{4pi }}I_{1}I_{2}oint _{C_{1}}oint _{C_{2}}{frac {dmathbf {l_{1}} mathbf {times } (dmathbf {l_{2}} mathbf {times } {hat {mathbf {r} }}_{21})}{r_{21}^{2}}}}

El campo magnético del segundo cable viene dado por:

{displaystyle mathbf {B} _{2}={frac {mu _{0}}{4pi }}I_{2}oint _{C_{2}}{frac {(dmathbf {l_{2}} mathbf {times } {hat {mathbf {r} }}_{21})}{r_{21}^{2}}}}

Así podemos reescribir la fuerza en el alambre 1 como:

{displaystyle mathbf {F} _{21}=I_{1}oint _{C_{1}}dmathbf {l_{1}} mathbf {times } mathbf {B} _{2}}

Ahora considere un segmento ${displaystyle dmathbf {l} }$ de un director desplazado ${displaystyle dmathbf {r} }$ en un campo magnético constante. El trabajo realizado se encuentra a partir de:

{displaystyle dW=dmathbf {F} cdot dmathbf {r} }

Si conectamos lo que encontramos antes ${displaystyle dmathbf {F} }$ Tenemos:

{displaystyle dW=(Idmathbf {l} mathbf {times } mathbf {B})cdot dmathbf {r} }

El área cubierta por el desplazamiento del conductor es:

{displaystyle dmathbf {S} =dmathbf {r} mathbf {times } dmathbf {l} }

Por lo tanto:

{displaystyle dW=Imathbf {B} cdot dmathbf {S} =IdPhi _{B}}

El trabajo diferencial también se puede dar en términos de cargo ${displaystyle dq}$ y posibles diferencias ${displaystyle V}$ :

{displaystyle dW=Vdq=VIdt}

Al igualar las dos ecuaciones para el trabajo diferencial llegamos a la Ley de Faraday.

{displaystyle dPhi _{B}=Vdt}

Además, ahora vemos que esto es sólo cierto si ${displaystyle dW}$ No es desvanecedor. Significado, la Ley de Faraday sólo es válida si el trabajo se realiza para producir el cambio de flujo.

Una forma matemática de validar la ley de Faraday en este tipo de situaciones es generalizar la definición de EMF como en la prueba de la ley de inducción de Faraday:

{displaystyle mathrm {EMF} =oint left(mathbf {E} +mathbf {v} times mathbf {B} right)cdot d{boldsymbol {ell }}}

El galvanometer normalmente sólo mide el primer término en el EMF que contribuye a la corriente en el circuito, aunque a veces puede medir la incorporación del segundo término como cuando el segundo término contribuye parte de la corriente que el galvanometer mide como EMF movido, por ejemplo en el experimento de disco de Faraday. En la situación anterior, el primer término es cero y sólo el primer término conduce una corriente que el galvanometer mide, por lo que no hay tensión inducida. Sin embargo, la Ley de Faraday todavía sostiene desde que el cambio aparente del flujo magnético va al segundo término en la generalización anterior de EMF. Pero no es medido por el galvanometer. Recuerda ${displaystyle mathbf {v} }$ es la velocidad local de un punto en el circuito, no un transportista de carga. Después de todo, ambas situaciones son consistentes con la preocupación de la relatividad y la microestructura de la materia, y/o la integridad de la ecuación Maxwell y la fórmula Lorentz, o la combinación de ellas, mecánica Hamiltoniana.

Más resultados...