Papiro matemático de Moscú

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

El Papiro Matemático de Moscú, también llamado Papiro Matemático de Golenishchev en honor a su primer propietario no egipcio, el egiptólogo Vladimir Golenishchev, es un papiro matemático del antiguo Egipto que contiene varios problemas en aritmética, geometría y álgebra. Golenishchev compró el papiro en 1892 o 1893 en Tebas. Posteriormente entró en la colección del Museo Estatal Pushkin de Bellas Artes de Moscú, donde permanece hoy.

Con base en la paleografía y ortografía del texto hierático, lo más probable es que el texto haya sido escrito en la XIII Dinastía y se base en material más antiguo que probablemente data de la Duodécima Dinastía de Egipto, aproximadamente en 1850 a.C. Aproximadamente 5,5 m (18 pies) de largo y variando entre 3,8 y 7,6 cm (1,5 y 3 pulgadas) de ancho, su formato fue dividido por el orientalista soviético Vasily Vasilievich Struve en 1930 en 25 problemas con soluciones.

Es un papiro matemático muy conocido, al que generalmente se hace referencia junto con el Papiro Matemático de Rhind. El Papiro Matemático de Moscú es más antiguo que el Papiro Matemático de Rhind, mientras que este último es el más grande de los dos.

Ejercicios contenidos en el Papiro de Moscú

Los problemas del Papiro de Moscú no siguen ningún orden particular y las soluciones de los problemas proporcionan mucho menos detalle que las del Papiro Matemático de Rhind. El papiro es bien conocido por algunos de sus problemas de geometría. Los problemas 10 y 14 calculan el área de superficie y el volumen de un tronco, respectivamente. Los problemas restantes son de naturaleza más común.

Problemas con piezas del barco

Los problemas 2 y 3 son problemas de piezas del barco. Uno de los problemas calcula la longitud del timón de un barco y el otro calcula la longitud del mástil de un barco dado que es 1/3 + 1/5 de la longitud de un tronco de cedro que originalmente era de 30 codos. largo.

Ajá problemas

ꜥḥꜥ (aha)
en jeroglíficos

Era: Nuevo Reino
(1550–1069 aC)

Problemas de aha implican encontrar cantidades desconocidas (referidos como aha, "estack") si se da la suma de la cantidad y parte(s) de ella. El papiro matemático Rhind también contiene cuatro de estos tipos de problemas. Los problemas 1, 19 y 25 del papiro de Moscú son problemas de Aha. Por ejemplo, el problema 19 pide a uno que calcule una cantidad tomada 1+1.2 y añadido a 4 para hacer 10. En otras palabras, en la notación matemática moderna uno se pide resolver ${\frac}x+4=10$ .

Problemas de Pefsu

La mayoría de los problemas son problemas de pefsu (ver: álgebra egipcia): 10 de los 25 problemas. Un pefsu mide la fuerza de la cerveza elaborada a partir de un hekat de grano.

{\mbox{pefsu}={\frac {\mbox{number loaves of pan (o jarras de cerveza)}}{\mbox{number of heqats of grain}}}

Un número de pefsu más alto significa pan o cerveza más débiles. El número pefsu se menciona en muchas listas de ofertas. Por ejemplo, el problema 8 se traduce como:

(1) Ejemplo de calcular 100 panes de pan de pefsu 20

(2) Si alguien te dice: "Tienes 100 panes de pan de pefsu 20

(3) para ser intercambiado por cerveza de pefsu 4

(4) como 1/2 1/4 cerveza fechada de malta"

(5) Calcula primero el grano requerido para los 100 panes del pan de pefsu 20

(6) El resultado es 5 heqat. Entonces recuérdese lo que necesita para un des-jug de cerveza como la cerveza llamada 1/2 1/4 cerveza de malta

(7) El resultado es 1/2 de la medida de heqat necesaria para el des-jug de la cerveza hecha de grano alto egipcio.

(8) Calcular 1/2 de 5 heqat, el resultado será 2 1/2

(9) Tome este 2 1/2 cuatro veces

10) El resultado es 10. Entonces le dices:

(11) "He aquí! La cantidad de cerveza es correcta".

Problemas de Bakú

Los problemas 11 y 23 son problemas de Bakú. Estos calculan la producción de los trabajadores. El problema 11 pregunta: si alguien trae 100 troncos que miden 5 por 5, ¿a cuántos troncos que miden 4 por 4 corresponde esto? El problema 23 encuentra el resultado de un zapatero dado que tiene que cortar y decorar sandalias.

Problemas de geometría

Siete de los veinticinco problemas son problemas de geometría y van desde calcular áreas de triángulos hasta encontrar el área de superficie de un hemisferio (problema 10) y encontrar el volumen de un tronco (una pirámide truncada).

Dos problemas de geometría

Problema 10

El décimo problema del Papiro Matemático de Moscú pide un cálculo del área de superficie de un hemisferio (Struve, Gillings) o posiblemente el área de un semicilindro (Peet). A continuación suponemos que el problema se refiere al área de un hemisferio.

El texto del problema 10 dice así: "Ejemplo de cálculo de una canasta. Te dan una canasta con boca de 4 1/2. ¿Cuál es su superficie? Tome 1/9 de 9 (ya que) la canasta es media cáscara de huevo. Obtienes 1. Calcula el resto, que es 8. Calcula 1/9 de 8. Obtienes 2/3 + 1/6 + 1/18. Encuentra el resto de este 8 después de restar 2/3 + 1/6 + 1/18. Obtienes 7 + 1/9. Multiplica 7 + 1/9 por 4 + 1/2. Obtienes 32. He aquí, esta es su área. Lo has encontrado correctamente."

La solución consiste en calcular el área como

{\text{Area}}=((2\times {\text{diameter})\times {\frac {8}{9}}})\times {\frac {8}}})\times {\text{diameter}={\frac {128}{81}}} {\text{diameter}}} {}}} {\f}} {\f}}}}}} {\f}}}}} {\f}} {\f}}}} {\f}}}}} {\f}}}}} {\f}}}}} {\f}}}}}}}}} {\f}}}}}}}}} {\f} {\f}}}} {\f}}}}}} {\f}}} {\f}}}}}}}}}}}}}}} {\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

La fórmula calcula para el área de un hemisferio, donde el escriba del papiro de Moscú utilizado ${\frac {256}\approx 3.16049$ a π aproximado.

Problema 14: Volumen del tronco de una pirámide cuadrada

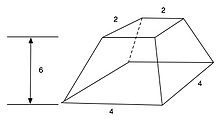
El decimocuarto problema de Matemáticas de Moscú calcula el volumen de un tronco.

El problema 14 establece que una pirámide ha sido truncada de tal manera que el área superior es un cuadrado de 2 unidades de longitud, la parte inferior un cuadrado de 4 unidades de longitud y la altura de 6 unidades, como se muestra. Se encuentra que el volumen es de 56 unidades cúbicas, lo cual es correcto.

El texto del ejemplo funciona así: "Si se le dice: una pirámide truncada de 6 para la altura vertical por 4 en la base por 2 en la parte superior: Usted debe cuadrado el 4; resultado 16. Usted debe duplicar 4; resultado 8. Usted debe cuadrado este 2; resultado 4. Usted debe añadir los 16 y los 8 y los 4; resultado 28. Usted debe tomar 1/3 de 6; resultado 2. Usted debe tomar 28 dos veces; resultado 56. Mira, es de 56. Encontrarás [lo] correcto"

La solución al problema indica que los egipcios conocían la fórmula correcta para obtener el volumen de una pirámide truncada:

V={3}h(a^{2}+ab+b^{2}

donde a y b son las longitudes de la base y los lados superiores de la pirámide truncada y h es la altura. Los investigadores han especulado cómo los egipcios podrían haber llegado a la fórmula para el volumen de un tronco, pero la derivación de esta fórmula no se da en el papiro.

Resumen

Richard J. Gillings dio un breve resumen del contenido del papiro. Números con líneas generales denotan la fracción de la unidad que tiene ese número como denominador, por ejemplo. ${\bar {4}={\frac} {1}{4}$ ; fracciones unidad eran objetos comunes de estudio en las matemáticas egipcias antiguas.

El contenido del papiro matemático de Moscú
No.	Detalle
1	Daño e imparable.
2	Daño e imparable.
3	Una mascota de cedro. ${\bar {}\;{\bar} {}$ de $30=16$ . No está claro.
4	Área de un triángulo. ${\bar {2}}$ de $4\times 10=20$ .
5	Pesus de panes y pan. Igual que el número 8.
6	Rectángulo, área $=12,b={\bar {2}\;{\bar {4}l$ . Encontrar $l$ y $b$ .
7	Triángulo, área $=20,h=2\;{\bar {2}b$ . Encontrar $h$ y $b$ .
8	Pesus de panes y pan.
9	Pesus de panes y pan.
10	Área de superficie curvada de un hemisferio (o cilindro).
11	Panes y canasta. Tío.
12	Pesu de cerveza. Tío.
13	Pesus de panes y cerveza. Igual que el número 9.
14	Volumen de una pirámide truncada. $V=(h/3)(a^{2}+ab+b^{2}$ .
15	Pesu de cerveza.
16	Pesu de cerveza. Similar al número 15.
17	Triángulo, área $=20,b=({\bar {3}\;{\bar {15}h$ . Encontrar $h$ y $b$ .
18	Tela de medición en codos y palmas. No está claro.
19	Resolver la ecuación $1\;{\bar}x+4=10$ . Despejado.
20	Pesu de 1000 panes. fracciones de horus-eye.
21	Mezcla de pan sacrificado.
22	Pesus de panes y cerveza. Cambio.
23	Computando el trabajo de un cobbler. No está claro. Peet dice muy difícil.
24	Intercambio de panes y cerveza.
25	Resolver la ecuación $2x+x=9$ . Elemental y claro.