Panal uniforme convexo

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Tiling espacial de polihedra uniforme convexa

El alternado de miel cúbica es una de las 28 tesselaciones uniformes de llenado de espacio en Euclidean 3-espacio, compuesta de tetrahedra amarilla alternante y octahedra roja.

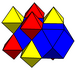
En geometría, un panal de abeja uniforme convexo es una teselación uniforme que llena el espacio euclidiano tridimensional con celdas poliédricas uniformes convexas que no se superponen.

Se conocen veintiocho panales de este tipo:

el panal cúbico familiar y 7 truncaciones;
el panal cúbico alterado y sus 4 truncas;
10 formas prismáticas basadas en los revestimientos uniformes de avión (11 si incluye el panal cúbico);
5 modificaciones de algunas de las anteriores por elongación y/o giro.

Pueden considerarse el análogo tridimensional de los mosaicos uniformes del plano.

El diagrama de Voronoi de cualquier red forma un panal uniforme convexo en el que las celdas son zonoedros.

Historia

1900: Thorold Gosset enumeró la lista de politopes convexos semiregulares con células regulares (sólidos platónicos) en su publicación Sobre las Figuras regulares y semi-regulares en el espacio de las dimensiones n, incluyendo un panal cúbico regular, y dos formas semiregulares con tetrahedra y octahedra.
1905: Alfredo Andreini enumera 25 de estas tessellations.
1991: manuscrito de Norman Johnson Uniform Polytopes identificó la lista de 28.
1994: Branko Grünbaum, en su papel Niveles uniformes de 3 espacios, también enumerado independientemente los 28, después de descubrir errores en la publicación de Andreini. Encontró el documento de 1905, que enumeraba 25, tenía 1 mal, y 4 desaparecidos. Grünbaum afirma en este documento que Norman Johnson merece prioridad para lograr la misma enumeración en 1991. También menciona que I. Alexeyev de Rusia había contactado con él con respecto a una enumeración puta de estas formas, pero que Grünbaum no pudo verificar esto en ese momento.
2006George Olshevsky, en su manuscrito Uniforme Panoploid Tetracombs, junto con la repetición de la lista derivada de 11 azulejos uniformes convexos, y 28 panales de miel uniformes convexos, expande una nueva lista derivada de 143 tetracombs uniformes convexos (Honeycombs of uniform 4-polytopes in 4-space).

Solo 14 de los poliedros uniformes convexos aparecen en estos patrones:

tres de los cinco sólidos platónicos (el tetraedro, cubo y octaedro),
seis de los trece sólidos arquímicos (los que tienen simetría tetraedral o sectaria reflexiva) y
cinco de la familia infinita de prismas (los 3, 4, 6-, 8- y 12-gonales; el prisma 4-gonal duplica el cubo).

El icosaedro, el cubo chato y el antiprisma cuadrado aparecen en algunas alternancias, pero esos panales no se pueden realizar con todas las aristas por unidad de longitud.

Nombres

Este conjunto puede denominarse panales regulares y semirregulares. Se le ha llamado los panales de Arquímedes por analogía con los poliedros convexos uniformes (no regulares), comúnmente llamados sólidos de Arquímedes. Recientemente, Conway ha sugerido nombrar el conjunto como Teselaciones arquitectónicas y los panales duales como Teselaciones catóptricas.

Los panales individuales se enumeran con los nombres que les dio Norman Johnson. (Algunos de los términos utilizados a continuación se definen en 4 politopos uniformes # Derivaciones geométricas para 46 4 politopos uniformes Wythoffianos no prismáticos)

Para referencias cruzadas, se dan con índices de lista de Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21–25, 31–34, 41–49, 51–52, 61–65) y Grünbaum(1-28). Coxeter usa δ₄ para un panal cúbico, hδ₄ para un panal cúbico alterno, qδ₄ para un panal cúbico cuarto, con subíndices para otros formas basadas en los patrones de anillos del diagrama de Coxeter.

Teselaciones uniformes euclidianas compactas (por sus infinitas familias de grupos de Coxeter)

Dominios fundamentales en un elemento cúbico de tres grupos.

correspondencias familiares

Los grupos de Coxeter infinitos fundamentales para el espacio tridimensional son:

El ${tilde {C}}_{3}$ , [4,3,4], cúbico, (8 formas únicas más una alternancia)
El ${tilde {B}}_{3}$ , [4,3]^1.1], alternado cúbico, (11 formas, 3 nuevas)
El ${tilde {A}}_{3}$ grupo cíclico [(3,3,3)] o [3]^[4]] (5 formas, una nueva)

Hay una correspondencia entre las tres familias. Eliminación de un espejo ${tilde {C}}_{3}$ productos ${tilde {B}}_{3}$ , y quitar un espejo de ${tilde {B}}_{3}$ productos ${tilde {A}}_{3}$ . Esto permite múltiples construcciones de los mismos panales de miel. Si las células son de color basadas en posiciones únicas dentro de cada construcción de Wythoff, estas diferentes simetrías se pueden mostrar.

Además, hay 5 panales especiales que no tienen simetría de reflexión pura y están construidos a partir de formas de reflexión con operaciones de alargamiento y giro.

El total de panales únicos anteriores es 18.

Las pilas prismáticas de infinitos grupos de Coxeter para 3 espacios son:

El ${tilde {C}}_{2}$ × ${tilde {I}}_{1}$ , [4,2] grupo prismático, (2 nuevas formas)
El ${tilde {G}}_{2}$ × ${tilde {I}}_{1}$ , [6,3,2] grupo prismático, (7 formas únicas)
El ${tilde {A}}_{2}$ × ${tilde {I}}_{1}$ , [(3,3),2,∞] grupo prismático, (No hay nuevas formas)
El ${tilde {I}}_{1}$ × ${tilde {I}}_{1}$ × ${tilde {I}}_{1}$ grupo prismático, (Estos se convierten en un Cuarto de miel)

Además, hay una forma especial alargada del panal prismático triangular.

El total de panales prismáticos únicos anteriores (excluyendo el cúbico contado anteriormente) es 10.

Combinando estos conteos, 18 y 10 nos da un total de 28 panales uniformes.

El grupo C̃3, [4,3,4] (cúbico)

El panal cúbico regular, representado por el símbolo de Schläfli {4,3,4}, ofrece siete panales uniformes derivados únicos a través de operaciones de truncamiento. (Se incluye una forma redundante, el panal de abeja cúbico runcinado, para completar, aunque es idéntica al panal de abeja cúbico.) La simetría de reflexión es el grupo afín de Coxeter [4,3,4]. Hay cuatro subgrupos de índice 2 que generan alternancias: [1⁺,4,3,4], [(4,3,4,2⁺)], [4,3⁺,4], y [4,3,4]⁺, con los dos primeros generados formas repetidas, y los dos últimos no son uniformes.

Combustibles de miel C3
Spacegroup	Fibrifold	Simetría ampliada	Extended diagrama	Orden	Combustibles de miel
Pm3m (221)	4⁻:2	[4,3,4]		× 1	1, 2, 3, 4, 5, 6
F m3m (225)	2⁻:2	[1]⁺,4,3,4] ↔ [4,3^1.1]	Administración	Medio	7, 11 12, 13
I43m (217)	4^o:2	[[4],3,4,2⁺)]		Medio × 2	(7),
Fd3m (227)	2⁺:2	[[1]⁺,4,3,4,1⁺]] Administración [[3]^[4]]]	Administración	Quarter × 2	10,
Im3m (229)	8^o:2	[[4,3,4]]		× 2	1) 8, 9

[4,3,4], grupo espacial Pm3m (221)
Referencia Índices	Nombre de Honeycomb Coxeter diagrama y el símbolo Schläfli	Cuentas/versión de células and positions in cubic honeycomb						Frames (Perspectiva)	Vertex figure	Celda doble
Referencia Índices	Nombre de Honeycomb Coxeter diagrama y el símbolo Schläfli	(0)	1)	2)	3)	Alt	Solids (Partial)	Frames (Perspectiva)	Vertex figure	Celda doble
J_11,15 A₁ W₁ G₂₂ δ₄	cúbico (chon) t₀{4,3,4} {4,3,4}				(8) (4.4.4)				octaedro	Cube,
J_12,32 A₁₅ W₁₄ G₇ O₁	rectificado cúbico (rico) t₁{4,3,4} r{4,3,4}	2) (3.3.3.3)			4) (3.4.3.4)				cuboide	Bipyramid cuadrado
J₁₃ A₁₄ W₁₅ G₈ t₁δ₄ O₁₅	truncado cúbico (tich) t_0,1{4,3,4} t{4,3,4}	1) (3.3.3.3)			4) (3.8.8.8)				pirámide cuadrada	pirámide cuadrada Isosceles
J₁₄ A₁₇ W₁₂ G₉ t_0,2δ₄ O₁₄	cantellated cubic (srich) t_0,2{4,3,4} rr{4,3,4}	1) (3.4.3.4)	2) (4.4.4)		2) (3.4.4.4)				prisma triangular oblicua	Bipirámide triangular
J₁₇ A₁₈ W₁₃ G₂₅ t_0,1,2δ₄ O₁₇	cantitruncated cubic (grich) t_0,1,2{4,3,4} tr{4,3,4}	1) (4.6.6)	1) (4.4.4)		2) (4.6.8)				irregular tetrahedron	pirámide triangular
J₁₈ A₁₉ W₁₉ G₂₀ t_0,1,3δ₄ O₁₉	(prich) t_0,1,3{4,3,4}	1) (3.4.4.4)	1) (4.4.4)	2) (4.4.8)	1) (3.8.8.8)				pirámide trapezoidal oblicua	Plaza pirámide
J_21,31,51 A₂ W₉ G₁ hδ₄ O₂₁	alternado cúbico (octet) h{4,3,4}				(8) (3.3.3)	(6) (3.3.3.3)			cuboctahedron	Dodecahedrille
J_22,34 A₂₁ W₁₇ G₁₀ h₂δ₄ O₂₅	Cantic cubic (tatoh) Administración	1) (3.4.3.4)			2) (3.6.6)	2) (4.6.6)			pirámide rectangular	Media oblate octahedrille
J₂₃ A₁₆ W₁₁ G₅ h₃δ₄ O₂₆	Runcic cubic (sratoh) Administración	1) (4.4.4)			1) (3.3.3)	3) (3.4.4.4)			prisma triangular cónico	Cubille
J₂₄ A₂₀ W₁₆ G₂₁ h_2,3δ₄ O₂₈	Runcicantic cubic (gratoh) Administración	1) (3.8.8.8)			1) (3.6.6)	2) (4.6.8)			Tetraedro irregular	Media pirámide
Nonuniform_b	snub rectified cubic (serch) sr{4,3,4}	1) (3.3.3.3.3)	1) (3.3.3)		2) (3.3.3.4)	4) (3.3.3)			Irr. tridiminished icosahedron
Nonuniform	Cantic snub cubic (casch) 2s₀{4,3,4}	1) (3.3.3.3.3)			2) (3.4.4.4)	3) (3.4.4)
Nonuniform	Esnub cúbico (rusca)	1) (3.4.3.4)	2) (4.4.4)	1) (3.3.3)	1) (3.6.6)	3) Tricupe
Nonuniform	Runcic cantitruncated cubic (esch) sr₃{4,3,4}	1) (3.3.3.4)	1) (4.4.4)	1) (4.4.4)	1) (3.4.4.4)	3) (3.4.4)

[[4,3,4]] panales de miel, grupo espacial Im3m (229)
Referencia Índices	Nombre de Honeycomb Coxeter diagrama y el símbolo Schläfli	Cuentas/versión de células and positions in cubic honeycomb			Solids (Partial)	Frames (Perspectiva)	Vertex figure	Celda doble
Referencia Índices	Nombre de Honeycomb Coxeter diagrama y el símbolo Schläfli	(0,3)	(1,2)	Alt	Solids (Partial)	Frames (Perspectiva)	Vertex figure	Celda doble
J_11,15 A₁ W₁ G₂₂ δ₄ O₁	portátil (como cúbico regular) (chon) t_0,3{4,3,4}	2) (4.4.4)	(6) (4.4.4)				octaedro	Cube
J₁₆ A₃ W₂ G₂₈ t_1,2δ₄ O₁₆	bitruncated cubic (batch) t_1,2{4,3,4} 2t{4,3,4}	4) (4.6.6)					(disphenoid)	Tetrahedrille oblato
J₁₉ A₂₂ W₁₈ G₂₇ t_0,1,2,3δ₄ O₂₀	cúbico omnitruncado (gippich) t_0,1,2,3{4,3,4}	2) (4.6.8)	2) (4.4.8)				irregular tetrahedron	Octava pirámide
J_21,31,51 A₂ W₉ G₁ hδ₄ O₂₇	Cuarto de miel cúbica (batatoh) h₀h₃{4,3,4}	2) (3.3.3)	(6) (3.6.6)				antiprisma triangular alargado	Cubillo oblato
J_21,31,51 A₂ W₉ G₁ hδ₄ O₂₁	Alternated runcinated cubic (octet) (Lo mismo como cúbico suplente) h_0,3{4,3,4}	2) (3.3.3)	(6) (3.3.3)	(6) (3.3.3.3)			cuboctahedron
Nonuniform	Biorthosnub cubic honeycomb (gabreth) 2s_0,3{4,2,4,3)}	2) (4.6.6)	2) (4.4.4)	2) (4.4.6)
Nonuniform_a	Alternated bitruncated cubic (bisch) h2t{4,3,4}	4) (3.3.3.3.3)		4) (3.3.3)
Nonuniform	Cantic bisnub cubico (cabisch) 2s_0,3{4,3,4}	2) (3.4.4.4)	2) (4.4.4)	2) (4.4.4)
Nonuniform_c	Alternated omnitruncated cubic (snich) h_0,1,2,3{4,3,4}	2) (3.3.3.4)	2) (3.3.3.4)	4) (3.3.3)

B̃3, grupo [4,31,1]

El ${tilde {B}}_{3}$ , [4,3] grupo ofrece 11 formas derivadas a través de operaciones de truncación, cuatro siendo únicos panales de miel uniformes. Hay 3 subgrupos índice 2 que generan alternaciones: [1]⁺,4,3^1.1[4,(3]^1.1)⁺], y [4,3]^1.1]⁺. El primero genera un repetido panal de miel, y los dos últimos no son uniformes pero se incluyen para la integridad.

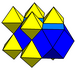
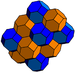
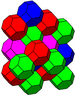
Los panales de este grupo se llaman cúbica alternada porque la primera forma puede verse como un panal cúbico con los vértices alternos eliminados, reduciendo las celdas cúbicas a tetraedros y creando un octaedro células en los huecos.

Los nodos se indexan de izquierda a derecha como 0,1,0',3 con 0' siendo inferior e intercambiable con 0. Los nombres cúbicos alternativos dados se basan en este orden.

B3 panales de miel
Spacegroup	Fibrifold	Simetría ampliada	Extended diagrama	Orden	Combustibles de miel
F m3m (225)	2⁻:2	[4,3]^1.1] ↔ [4,3,4,1⁺]	Administración	× 1	1, 2, 3, 4
F m3m (225)	2⁻:2	[1]⁺,4,3^1.1] ↔ 3^[4]]	Administración	× 2	1) 3)
Pm3m (221)	4⁻:2	[4,3]^1.1]		× 2	5, 6, 7, (6), 9, 10, 11

[4,3]^1.1* panales de miel uniformes, grupo espacial Fm3m (225)
Referencia índices	Nombre de Honeycomb Coxeter diagramas	Celdas por ubicación (y contar alrededor de cada vértice)				Solids (Partial)	Frames (Perspectiva)	figura del vértice
Referencia índices	Nombre de Honeycomb Coxeter diagramas	(0)	1)	(0')	3)	Solids (Partial)	Frames (Perspectiva)	figura del vértice
J_21,31,51 A₂ W₉ G₁ hδ₄ O₂₁	Alternated cubic (octet) Administración			(6) (3.3.3.3)	(8) (3.3.3)			cuboctahedron
J_22,34 A₂₁ W₁₇ G₁₀ h₂δ₄ O₂₅	Cantic cubic (tatoh) Administración	1) (3.4.3.4)		2) (4.6.6)	2) (3.6.6)			pirámide rectangular
J₂₃ A₁₆ W₁₁ G₅ h₃δ₄ O₂₆	Runcic cubic (sratoh) Administración	1) cube		3) (3.4.4.4)	1) (3.3.3)			prisma triangular cónico
J₂₄ A₂₀ W₁₆ G₂₁ h_2,3δ₄ O₂₈	Runcicantic cubic (gratoh) Administración	1) (3.8.8.8)		2) (4.6.8)	1) (3.6.6)			Tetraedro irregular

[4,3]^1.1] panales de miel uniformes, grupo espacial Pm3m (221)
Referencia índices	Nombre de Honeycomb Coxeter diagramas Administración	Celdas por ubicación (y contar alrededor de cada vértice)				Solids (Partial)	Frames (Perspectiva)	figura del vértice
Referencia índices	Nombre de Honeycomb Coxeter diagramas Administración	(0,0')	1)	3)	Alt	Solids (Partial)	Frames (Perspectiva)	figura del vértice
J_11,15 A₁ W₁ G₂₂ δ₄ O₁	Cubic (chon) Administración	(8) (4.4.4)						octaedro
J_12,32 A₁₅ W₁₄ G₇ t₁δ₄ O₁₅	Rectificado cúbico (rico) Administración	4) (3.4.3.4)		2) (3.3.3.3)				cuboide
J_12,32 A₁₅ W₁₄ G₇ t₁δ₄ O₁₅	Rectificado cúbico (rico) Administración	2) (3.3.3.3)		4) (3.4.3.4)				cuboide
J₁₃ A₁₄ W₁₅ G₈ t_0,1δ₄ O₁₄	Truncated cubic (tich) Administración	4) (3.8.8.8)		1) (3.3.3.3)				pirámide cuadrada
J₁₄ A₁₇ W₁₂ G₉ t_0,2δ₄ O₁₇	Cantellated cubic (srich) Administración	2) (3.4.4.4)	2) (4.4.4)	1) (3.4.3.4)				obilique triangular prism
J₁₆ A₃ W₂ G₂₈ t_0,2δ₄ O₁₆	Bitruncated cubic (batch) Administración	2) (4.6.6)		2) (4.6.6)				isosceles tetrahedron
J₁₇ A₁₈ W₁₃ G₂₅ t_0,1,2δ₄ O₁₈	Cantitruncated cubic (grich) Administración	2) (4.6.8)	1) (4.4.4)	1) (4.6.6)				irregular tetrahedron
J_21,31,51 A₂ W₉ G₁ hδ₄ O₂₁	Alternated cubic (octet) Administración	(8) (3.3.3)			(6) (3.3.3.3)			cuboctahedron
J_22,34 A₂₁ W₁₇ G₁₀ h₂δ₄ O₂₅	Cantic cubic (tatoh) Administración	2) (3.6.6)		1) (3.4.3.4)	2) (4.6.6)			pirámide rectangular
Nonuniform_a	Alternated bitruncated cubic (bisch) Administración	2) (3.3.3.3.3)		2) (3.3.3.3.3)	4) (3.3.3)
Nonuniform_b	Alternated cantitruncated cubic (serch) Administración	2) (3.3.3.4)	1) (3.3.3)	1) (3.3.3.3.3)	4) (3.3.3)			Irr. tridiminished icosahedron

Ã3, [3[4]] grupo

Hay 5 formas construidas a partir de ${tilde {A}}_{3}$ [3]^[4]] Grupo Coxeter, del cual sólo el cuarto de baño de miel es único. Hay un subgrupo índice 2 [3^[4]]⁺ que genera la forma de snub, que no es uniforme, pero incluido para la integridad.

Combustibles de miel A3
Spacegroup	Fibrifold	Simetría cuadrada	Simetría ampliada	Extended diagrama	Extended grupo	Diagramas de panal
F43m (216)	1^o:2	a1	[3]^[4]]		${tilde {A}}_{3}$	(None)
F m3m (225)	2⁻:2	d2	[3]^[4]] ↔ [4,3^1.1]	Administración	${tilde {A}}_{3}$ × 2₁ Administración ${tilde {B}}_{3}$	₁,₂
Fd3m (227)	2⁺:2	g2	[[3]^[4]]] o [2]⁺[3]^[4]]]	Administración	${tilde {A}}_{3}$ × 2₂	₃
Pm3m (221)	4⁻:2	d4	[3]^[4]] ↔ [4,3,4]	Administración	${tilde {A}}_{3}$ ×4₁ Administración ${tilde {C}}_{3}$	₄
I3 (204)	8^−o	r8	[4[3]^[4]]]⁺ [4.3]⁺,4]]	Administración	1⁄2 ${tilde {A}}_{3}$ × 8 1⁄2 ${tilde {C}}_{3}$ × 2	_(*)
Im3m (229)	8^o:2	r8	[4[3]^[4]]] ↔ [[4,3,4]]	Administración	${tilde {A}}_{3}$ × 8 Administración ${tilde {C}}_{3}$ × 2	₅

[[3]^[4]]] panales de miel uniformes, grupo espacial Fd3m (227)
Referencia índices	Nombre de Honeycomb Coxeter diagramas	Celdas por ubicación (y contar alrededor de cada vértice)		Solids (Partial)	Frames (Perspectiva)	figura del vértice
Referencia índices	Nombre de Honeycomb Coxeter diagramas	(0,1)	(2,3)	Solids (Partial)	Frames (Perspectiva)	figura del vértice
J_25,33 A₁₃ W₁₀ G₆ qδ₄ O₂₇	cuarto cúbico (batatoh) Administración q{4,3,4}	2) (3.3.3)	(6) (3.6.6)			antiprisma triangular

[3]^[4][4,3]^1.1* panales de miel uniformes, grupo espacial Fm3m (225)
Referencia índices	Nombre de Honeycomb Coxeter diagramas Administración	Celdas por ubicación (y contar alrededor de cada vértice)			Solids (Partial)	Frames (Perspectiva)	figura del vértice
Referencia índices	Nombre de Honeycomb Coxeter diagramas Administración	0	(1,3)	2	Solids (Partial)	Frames (Perspectiva)	figura del vértice
J_21,31,51 A₂ W₉ G₁ hδ₄ O₂₁	alternado cúbico (octet) Administración Administración h{4,3,4}		(8) (3.3.3)	(6) (3.3.3.3)			cuboctahedron
J_22,34 A₂₁ W₁₇ G₁₀ h₂δ₄ O₂₅	cántico cúbico (tatoh) Administración Administración h₂{4,3,4}	2) (3.6.6)	1) (3.4.3.4)	2) (4.6.6)			pirámide rectangular

[2[3]^[4]]] ↔ [4,3,4]3m (221)
Referencia índices	Nombre de Honeycomb Coxeter diagramas Administración	Celdas por ubicación (y contar alrededor de cada vértice)		Solids (Partial)	Frames (Perspectiva)	figura del vértice
Referencia índices	Nombre de Honeycomb Coxeter diagramas Administración	(0,2)	(1,3)	Solids (Partial)	Frames (Perspectiva)	figura del vértice
J_12,32 A₁₅ W₁₄ G₇ t₁δ₄ O₁	rectificado cúbico (rico) Administración Administración Administración r{4,3,4}	2) (3.4.3.4)	1) (3.3.3.3)			cuboide

[4[3]^[4]]] ↔ [4,3,4] Im3m (229)
Referencia índices	Nombre de Honeycomb Coxeter diagramas Administración Administración	Celdas por ubicación (y contar alrededor de cada vértice)		Solids (Partial)	Frames (Perspectiva)	figura del vértice
Referencia índices		(0,1,2,3)	Alt	Solids (Partial)	Frames (Perspectiva)	figura del vértice
J₁₆ A₃ W₂ G₂₈ t_1,2δ₄ O₁₆	bitruncated cubic (batch) Administración Administración 2t{4,3,4}	4) (4.6.6)				isosceles tetrahedron
Nonuniform_a	Alternated cantitruncated cubic (bisch) Administración Administración h2t{4,3,4}	4) (3.3.3.3.3)	4) (3.3.3)

Formas no wythoffianas (giratorias y alargadas)

Se generan tres panales más uniformes rompiendo uno u otro de los panales anteriores donde sus caras forman un plano continuo, luego rotando capas alternas 60 o 90 grados (giro) y/o insertando un capa de prismas (alargamiento).

Los mosaicos cúbicos alternados alargados y giroalargados tienen la misma figura de vértice, pero no son iguales. En la forma alargada, cada prisma se encuentra con un tetraedro en un extremo triangular y un octaedro en el otro. En la forma giroelongada, los prismas que se encuentran con tetraedros en ambos extremos se alternan con prismas que se encuentran con octaedros en ambos extremos.

El mosaico prismático triangular giroelongado tiene la misma figura de vértice que uno de los mosaicos prismáticos simples; los dos pueden derivarse de los mosaicos prismáticos triangulares planos y giratorios, respectivamente, mediante la inserción de capas de cubos.

Referencia índices	símbolo	Nombre de Honeycomb	tipos de células (# en cada vértice)	figura del vértice
J₅₂ A_{2 '} G₂ O₂₂	h{4,3,4}:g	gyrated alternad cubic (gytoh)	tetraedro (8) octaedro (6)	triangular orthobicupola
J₆₁ A_? G₃ O₂₄	h{4,3,4}:ge	gyroelongated alternad cubic (gyetoh)	prisma triangular (6) tetraedro (4) octaedro (3)
J₆₂ A_? G₄ O₂₃	h{4,3,4}:e	elongated alternad cubic (etoh)	prisma triangular (6) tetraedro (4) octaedro (3)
J₆₃ A_? G₁₂ O₁₂	{3,6}:g × {∞}	gyrated triangular prismatic (gytoph)	prisma triangular (12)
J₆₄ A_? G₁₅ O₁₃	{3,6}:ge × {∞}	gyroelongated triangular prismatic (gyetaph)	prisma triangular (6) cubo (4)

Pilas prismáticas

Once mosaicos prismáticos se obtienen apilando los once mosaicos planos uniformes, que se muestran a continuación, en capas paralelas. (Uno de estos panales es el cúbico, que se muestra arriba). La figura del vértice de cada uno es una bipirámide irregular cuyas caras son triángulos isósceles.

El C̃2×Ĩ1(∞), [4,4,2,∞], grupo prismático

Solo hay 3 panales únicos del mosaico cuadrado, pero los 6 truncamientos de mosaico se enumeran a continuación para completar, y las imágenes de mosaico se muestran con los colores correspondientes a cada forma.

Índices	Coxeter-Dynkin y Schläfli símbolos	Nombre de Honeycomb	Plane azulejos
J_11,15 A₁ G₂₂	{4,4}×{∞}	Cubic (Square prismatic) (chon)	(4.4.4.4)
	r{4,4}×{∞}
	rr{4,4}×{∞}
J₄₅ A₆ G₂₄	t{4,4}×{∞}	Truncated/Bitruncated square prismatic (tassiph)	(4.8.8)
J₄₅ A₆ G₂₄	tr{4,4}×{∞}	Truncated/Bitruncated square prismatic (tassiph)	(4.8.8)
J₄₄ A₁₁ G₁₄	sr{4,4}×{∞}	Snub cuadrado prismático (sassiph)	(3.3.4.3.4)
Nonuniform	h_0,1,2,3{4,2,00}

El grupo prismático G̃2xĨ1(∞), [6,3,2,∞]

Índices	Coxeter-Dynkin y Schläfli símbolos	Nombre de Honeycomb	Plane azulejos
J₄₁ A₄ G₁₁	{3,6} × {}	Triangular prismatic (tiph)	(36)
J₄₂ A₅ G₂₆	{6,3}	Hexagonal prismatic (hiph)	(63)
J₄₂ A₅ G₂₆	t{3,6} × {∞}	Hexagonal prismatic (hiph)	(63)
J₄₃ A₈ G₁₈	r{6,3}	Trihexagonal prismatic (thiph)	(3.6.3.6)
J₄₆ A₇ G₁₉	t{6,3}	Truncated hexagonal prismatic (thaph)	(3.12.12)
J₄₇ A₉ G₁₆	rr{6,3} × {∞}	Rhombi-trihexagonal prismatic (srothaph)	(3.4.6.4)
J₄₈ A₁₂ G₁₇	sr{6,3}	Snub hexagonal prismatic (snathaph)	(3.3.3.6)
J₄₉ A₁₀ G₂₃	tr{6,3} × {∞}	truncated trihexagonal prismatic (grothaph)	(4.6.12)
J₆₅ A_{11 '} G₁₃	{3,6}:e × {∞}	elongated triangular prismatic (etoph)	(3.3.3.4.4)
J₅₂ A_{2 '} G₂	h3t{3,6,2}	gyrated tetrahedral-octahedral (gytoh)	(36)
J₅₂ A_{2 '} G₂	s2r{3,6,2, propuesto}	gyrated tetrahedral-octahedral (gytoh)	(36)
Nonuniform	h_0,1,2,3{3,6,2}

Enumeración de formas de Wythoff

Todas las construcciones Wythoff no prismáticas de los grupos de Coxeter se dan a continuación, junto con sus alternancias. Las soluciones uniformes están indexadas con la lista de Branko Grünbaum. Los fondos verdes se muestran en panales repetidos, y las relaciones se expresan en los diagramas de simetría extendidos.

Coxeter group	Simetría ampliada	Combustibles de miel		Chiral prórroga simetría	Alternation honeycombs
[4,3,4]	[4,3,4]	6	₂₂ Silencio ₇ Silencio ₈ ₉ Silencio ₂₅ Silencio ₂₀	[1]⁺,4,3⁺,4,1⁺]	2)	₁ Silencio _b
	[2]⁺[4,3,4] =	1)	₂₂	[2]⁺[4.3]⁺,4,2⁺)]	1)	₁ Silencio ₆
	[2]⁺[4,3,4]	1	₂₈	[2]⁺[4.3]⁺,4,2⁺)]	1)	_a
	[2]⁺[4,3,4]	2	₂₇	[2]⁺[4,3,4]⁺	1)	_c
[4,3]^1.1]	[4,3]^1.1]	4	₁ Silencio ₇ Silencio ₁₀ Silencio ₂₈
	[1[4,3]^1.1]]=[4,3,4] =	(7)	₂₂ Silencio ₇ Silencio ₂₂ Silencio ₇ Silencio ₉ Silencio ₂₈ Silencio ₂₅	[1[1]⁺,4,3^1.1]]⁺	2)	₁ Silencio ₆ Silencio _a
	[1[4,3]^1.1]]=[4,3,4] =	(7)		[1[4,3]^1.1]]⁺ =[4,3,4]⁺	1)	_b
[3]^[4]]	[3]^[4]]	(none)
	[2]⁺[3]^[4]]]	1	₆
	[1[3]^[4]]=[4,3]^1.1] =	2)	₁ Silencio ₁₀
	[2[3]^[4]]]=[4,3,4] =	1)	₇
	[(2)⁺,4)[3^[4][2]⁺[4,3,4] =	1)	₂₈	[(2)⁺,4)[3^[4]]]⁺ [2]⁺[4,3,4]⁺	1)	_a

Ejemplos

Las 28 teselaciones se encuentran en arreglos de cristal.

El panal cúbico alternado es de especial importancia ya que sus vértices forman un compacto empaquetamiento cúbico de esferas. El armazón que llena el espacio de octaedros y tetraedros empaquetados aparentemente fue descubierto por primera vez por Alexander Graham Bell y redescubierto de forma independiente por Buckminster Fuller (quien lo llamó el armazón octeto y lo patentó en la década de 1940). [3] [4] [5] [6]. Las armaduras de octeto se encuentran ahora entre los tipos de armaduras más comunes que se utilizan en la construcción.

Formas de friso

Si se permite que las celdas sean mosaicos uniformes, se pueden definir panales más uniformes:

Familias:

${tilde {C}}_{2}$ × $A_{1}$ [4,4,2] Cofres de miel de losas cúbicas (3 formularios)
${tilde {G}}_{2}$ × $A_{1}$ [6,3,2] Tri-hexagonal slab honeycombs (8 formas)
${tilde {A}}_{2}$ × $A_{1}$ [(3,3),2] Panallas triangulares (No hay nuevas formas)
${tilde {I}}_{1}$ × $A_{1}$ × $A_{1}$ : [∞,2,2] = Cubic column honeycombs (1 formulario)
$I_{2}(p)$ × ${tilde {I}}_{1}$ [p,2, hígado] Combustibles de columna poligonal (análogo a los duoprismos: estos parecen una torre infinita única de prismas p-gonales, con el espacio restante lleno de prismas apeirogonales)
${tilde {I}}_{1}$ × ${tilde {I}}_{1}$ × $A_{1}$ [viejos,2, vivos,2] = [4,2] = (Igual que la familia de panal de losas cúbicas)

Ejemplos (partialmente sorteados)
Cubic slab honeycomb	Alternated hexagonal slab honeycomb	Trihexagonal slab honeycomb

4) 4³: cubo 1) 4⁴: azulejo cuadrado	4) 3³: tetraedro 3) 3⁴: octaedro 1) 3⁶: azulejo triangular	2) 3.4.4: prisma triangular 2) 4.4.6: prisma hexagonal 1) (3.6)²: azulejo trihexagonal

Las dos primeras formas que se muestran arriba son semirregulares (uniformes con solo facetas regulares), y Thorold Gosset las enumeró en 1900, respectivamente, como semicontrol 3-ic y tetroctaédrica semi- comprobar.

Panal de abeja escaliforme

Un panal de abeja scaliforme es de vértice transitivo, como un panal de abeja uniforme, con caras poligonales regulares, mientras que las celdas y los elementos superiores solo necesitan ser orbiformes, equiláteros, con sus vértices sobre hiperesferas. Para panales 3D, esto permite un subconjunto de sólidos de Johnson junto con los poliedros uniformes. Algunos escaliformes pueden generarse por un proceso de alternancia, dejando, por ejemplo, huecos de pirámide y cúpula.

Escaliformas de panal Euclidean
Losas frisos			Montajes prismáticos
s₃{2,6,3},	s₃{2,4,4},	s{2,4,4},	3s₄4.4,2;


1) 3.4.3.4: cúpula triangular 2) 3.4.6: cúpula triangular (1) 3.3.3.3: octaedron (1) 3.6.3.6: Tiling trihexagonal	(1) 3.4.4.4: cúpula cuadrada (2) 3.4.8: cúpula cuadrada (1) 3.3.3: tetraedro (1) 4.8.8: azulejos cuadrados truncados	(1) 3.3.3: pirámide cuadrada (4) 3.3.4: pirámide cuadrada (4) 3.3.3: tetraedro 1) 4.4.4.4: revestimiento cuadrado	(1) 3.3.3: pirámide cuadrada (4) 3.3.4: pirámide cuadrada (4) 3.3.3: tetraedro (4) 4.4.4: cubo

Formas hiperbólicas

The order-4 dodecahedral honeycomb, {5,3,4} en perspectiva

The paracompact hexagonal tiling honeycomb, {6,3,3}, in perspective

Hay 9 familias de grupos de Coxeter de panales compactos uniformes en 3 espacios hiperbólicos, generados como construcciones de Wythoff y representados por permutaciones de anillos de los diagramas de Coxeter-Dynkin para cada familia.

De estas 9 familias, hay un total de 76 panales únicos generados:

[3,5,3]: - 9 formas
[5,3,4]: - 15 formas
[5,3,5]: - 9 formas
[5,3]^1.1] - 11 formas (7 solapadas con [5,3,4] familia, 4 son únicas)
[(4,3,3,3)]: - 9 formas
[(4,3,4,3)]: - 6 formas
[(5,3,3,3)]: - 9 formas
[(5,3,4,3)]: - 9 formas
[(5,3,5,3)]: - 6 formas

Se conocen varias formas no Wythoffianas fuera de la lista de 76; no se sabe cuántos hay.

Formas hiperbólicas paracompactas

También hay 23 grupos de Coxeter paracompactos de rango 4. Estas familias pueden producir panales uniformes con facetas ilimitadas o figura de vértice, incluidos los vértices ideales en el infinito:

Simplectic hyperbolic paracompact group summary
Tipo	Coxeter groups	Conteo único de panal
Gráficos lineales	Silencio Silencio Silencio Silencio Silencio Silencio	4×15+6+8 = 82
Gráficos tridentales	Silencio Silencio	4+4+0 = 8
Gráficos cólicos	Silencio Silencio Silencio Silencio Silencio Silencio Silencio Silencio	4×9+5+1+4+1+0 = 47
Gráficos de cola	Silencio Silencio Silencio	4+4+2 = 14

Contenido relacionado

Más resultados...