Oscilación de plasma

Las Oscilaciones del plasma, también conocidas como ondas de Langmuir (en honor a Irving Langmuir), son oscilaciones rápidas de la densidad electrónica en medios conductores como plasmas o metales en la región ultravioleta. . Las oscilaciones pueden describirse como una inestabilidad en la función dieléctrica de un gas de electrones libres. La frecuencia depende sólo débilmente de la longitud de onda de la oscilación. La cuasipartícula resultante de la cuantificación de estas oscilaciones es el plasmón.

Las ondas de Langmuir fueron descubiertas por los físicos estadounidenses Irving Langmuir y Lewi Tonks en la década de 1920. Tienen una forma paralela a las ondas de inestabilidad de Jeans, que son causadas por inestabilidades gravitacionales en un medio estático.

Mecanismo

Considere un plasma eléctricamente neutro en equilibrio, formado por un gas de iones cargados positivamente y electrones cargados negativamente. Si se desplaza una pequeña cantidad de un electrón o un grupo de electrones con respecto a los iones, la fuerza de Coulomb atrae a los electrones hacia atrás, actuando como una fuerza restauradora.

'Frío' electrones

Si se ignora el movimiento térmico de los electrones, es posible demostrar que la densidad de carga oscila a la frecuencia del plasma

⋅ ⋅ pe=nee2mAlternativa Alternativa ε ε 0,[rad/s]{displaystyle omega _{mathrm {pe} }={sqrt {frac {fn} {cHFF} {cH00} {cH00}varepsilon} ¿Por qué? (unidades de ISI)

⋅ ⋅ pe=4π π nee2mAlternativa Alternativa ,[rad/s]{displaystyle omega _{mathrm {pe} }={sqrt {frac {4fncH00} No. ¿Qué? left[mathrm {rad/s} right] (unidades g)

Donde ne{displaystyle n_{mathrm {}} es la densidad número de electrones, e{displaystyle e} es la carga eléctrica, mAlternativa Alternativa {displaystyle m^{*} es la masa efectiva del electrón, y ε ε 0{displaystyle varepsilon ¿Qué? es la autorización del espacio libre. Tenga en cuenta que la fórmula anterior se deriva bajo la aproximación que la masa ion es infinita. Esto es generalmente una buena aproximación, ya que los electrones son mucho más ligeros que los iones.

Prueba de usar ecuaciones de Maxwell. Suponiendo oscilaciones de densidad de carga *** *** ()⋅ ⋅ )=*** *** 0e− − i⋅ ⋅ t{displaystyle rho (omega)=rho ¿Qué? la ecuación de continuidad:

Silencio Silencio ⋅ ⋅ j=− − ∂ ∂ *** *** ∂ ∂ t=i⋅ ⋅ *** *** ()⋅ ⋅ ){displaystyle nabla cdot mathbf {j} =-{frac {partial rho }{partial t}}=iomega rho (omega)}

Silencio Silencio ⋅ ⋅ E()⋅ ⋅ )=4π π *** *** ()⋅ ⋅ ){displaystyle nabla cdot mathbf {E} (omega)=4pirho (omega)}

j()⋅ ⋅ )=σ σ ()⋅ ⋅ )E()⋅ ⋅ ){displaystyle mathbf {j} (omega)=sigma (omega)mathbf {E} (omega)}

i⋅ ⋅ *** *** ()⋅ ⋅ )=4π π σ σ ()⋅ ⋅ )*** *** ()⋅ ⋅ ){displaystyle iomega rho (omega)=4pi sigma (omega)rho (omega)}

1+4π π iσ σ ()⋅ ⋅ )⋅ ⋅ =0{displaystyle 1+{frac {4pi isigma (omega)}{omega }=0}

ε ε ()⋅ ⋅ )=1+4π π iσ σ ()⋅ ⋅ )⋅ ⋅ {displaystyle epsilon (omega)=1+{frac {4pi isigma (omega)}{omega }

ε ε ≥ ≥ 0{displaystyle epsilon geq 0}

⋅ ⋅ p{displaystyle omega _{rm {p}}

ε ε =0{displaystyle epsilon =0}

Esta expresión debe modificarse en el caso de los plasmas de electrones y positrones, que se encuentran a menudo en astrofísica. Dado que la frecuencia es independiente de la longitud de onda, estas oscilaciones tienen una velocidad de fase infinita y una velocidad de grupo cero.

Note eso, cuando mAlternativa Alternativa =me{displaystyle - ¿Qué?, la frecuencia de plasma, ⋅ ⋅ pe{displaystyle omega _{mathrm {pe}}, depende sólo de las constantes físicas y densidad de electrones ne{displaystyle n_{mathrm {}}. La expresión numérica para frecuencia de plasma angular es

fPe=⋅ ⋅ Pe2π π [Hz]{displaystyle {fnMiga*}{text{f}} {f}}}}}mfnh}} {fnh}}}}}m}}}}}m}}} {fnfnK}f}}fnf}}f}f}fnfnh}

Los metales son sólo transparentes a la luz con una frecuencia mayor que la frecuencia plasmática del metal. Para metales típicos como aluminio o plata, ne{displaystyle n_{mathrm {}} aproximadamente 10²³ cm⁻³, que trae la frecuencia de plasma a la región ultravioleta. Por eso la mayoría de los metales reflejan la luz visible y parecen brillantes.

'Cálido' electrones

Cuando los efectos de la velocidad térmica del electrón ve,th=kBTe/me{fnMicrosoft Sans Serif}={sqrt {k_{mathrm} {B}T_{mathrm {e}/m_{mathrm {e}}}} {}}} {}}}} {}}}}}} {}}}}}}}} {}} {}}}}}}}} {}}} {}}}}}}} se tienen en cuenta, la presión electrones actúa como fuerza restauradora, así como el campo eléctrico y las oscilaciones se propagan con frecuencia y número de onda relacionados por la onda longitudinal Langmuir:

⋅ ⋅ 2=⋅ ⋅ pe2+3kBTemek2=⋅ ⋅ pe2+3k2ve,th2,{displaystyle omega ^{2}=omega _{mathrm {pe} ################################################################################################################################################################################################################################################################ } k^{2}=omega ¿Qué? }{2}+3k^{2}v_{mathrm {e,th} {2}}}

3⋅ ⋅ ve,th{displaystyle {sqrt {3}cdot v_{mathrm {e,th}}

v♪ ♪ vph =def ⋅ ⋅ k,{displaystyle vsim v_{mathrm {ph} {fnK} {fnK}}} {fnMicroc {omega} {fnK}}}

En un plasma limitado, los campos eléctricos marginales pueden provocar la propagación de oscilaciones del plasma, incluso cuando los electrones están fríos.

En un metal o semiconductor, el efecto de los iones' Se debe tener en cuenta el potencial periódico. Esto generalmente se hace usando los electrones' masa efectiva en lugar de m.

Oscilaciones del plasma y el efecto de la masa negativa

Las oscilaciones de plasma pueden dar lugar al efecto de la “masa negativa”. El modelo mecánico que da lugar al efecto de masa efectivo negativo se representa en Gráfico 1. Un núcleo con masa m2{displaystyle # se conecta internamente a través de la primavera con constante k2{displaystyle K_{2} a un proyectil con masa m1{displaystyle m_{1}. El sistema está sujeto a la fuerza sinusoidal externa F()t)=F^ ^ pecado⁡ ⁡ ⋅ ⋅ t{displaystyle F(t)={widehat {F}sin omega t}. Si resolvemos las ecuaciones del movimiento para las masas m1{displaystyle m_{1} y m2{displaystyle # y reemplazar todo el sistema con una sola masa efectiva meff{displaystyle # obtenemos:

meff=m1+m2⋅ ⋅ 02⋅ ⋅ 02− − ⋅ ⋅ 2,{displaystyle m_{2}omega ################################################################################################################################################################################################################################################################ ¿Qué?

⋅ ⋅ 0=k2/m2{textstyle omega ¿Qué? {k_{2}/m_{2}}}

⋅ ⋅ {displaystyle omega }

⋅ ⋅ 0{displaystyle omega ¿Qué?

meff{displaystyle #

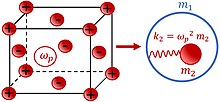
La masa negativa efectiva (densidad) también se hace posible basándose en el acoplamiento electromecánico que explota las oscilaciones plasmáticas de un gas electrón libre (ver Gráfico 2). La masa negativa aparece como resultado de la vibración de una partícula metálica con una frecuencia de ⋅ ⋅ {displaystyle omega } que cierra la frecuencia de las oscilaciones plasmáticas del gas electrón m2{displaystyle # relativamente a la celosa iónica m1{displaystyle m_{1}. Las oscilaciones de plasma están representadas con la primavera elástica k2=⋅ ⋅ p2m2{displaystyle k_{2}=omega _{rm {p} {2}m_{2}, donde ⋅ ⋅ p{displaystyle omega _{rm {p}} es la frecuencia plasmática. Así, la partícula metálica vibrada con la frecuencia externa ⋅ se describe por la masa efectiva

meff=m1+m2⋅ ⋅ p2⋅ ⋅ p2− − ⋅ ⋅ 2,{displaystyle m_{2}omega ################################################################################################################################################################################################################################################################ {p}} {2}-omega } {2}}}

⋅ ⋅ {displaystyle omega }

⋅ ⋅ p{displaystyle omega _{rm {p}}