Orbitales atómicos

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

En teoría atómica y mecánica cuántica, un orbital atómico es una función que describe la ubicación y el comportamiento ondulatorio de un electrón en un átomo. Esta función se puede utilizar para calcular la probabilidad de encontrar cualquier electrón de un átomo en cualquier región específica alrededor del núcleo del átomo. El término orbital atómico también puede referirse a la región física o espacio donde se puede calcular que está presente el electrón, según lo predicho por la forma matemática particular del orbital.

Cada orbital en un átomo se caracteriza por un conjunto de valores de los tres números cuánticos n, ℓ y m _l, que corresponden respectivamente a la energía del electrón, el momento angular y un componente del vector de momento angular (número cuántico magnético). Como alternativa al número cuántico magnético, los orbitales suelen estar etiquetados por los polinomios armónicos asociados (p. ej., xy, x − y). Cada uno de estos orbitales puede estar ocupado por un máximo de dos electrones, cada uno con su propia proyección de espín $milisegundo}$ . Los nombres simples orbital s, orbital p, orbital d y orbital fse refieren a orbitales con número cuántico de momento angular ℓ = 0, 1, 2 y 3 respectivamente. Estos nombres, junto con el valor de n, se utilizan para describir las configuraciones electrónicas de los átomos. Se derivan de la descripción por parte de los primeros espectroscopistas de ciertas series de líneas espectroscópicas de metales alcalinos como nítidas, principales , difusas y fundamentales. Los orbitales para ℓ > 3 continúan alfabéticamente (g, h, i, k,...), omitiendo j porque algunos idiomas no distinguen entre las letras "i" y "j".

Los orbitales atómicos son los componentes básicos del modelo de orbitales atómicos (o nube de electrones o modelo de mecánica ondulatoria), un marco moderno para visualizar el comportamiento submicroscópico de los electrones en la materia. En este modelo, la nube de electrones de un átomo puede verse como construida (en aproximación) en una configuración electrónica que es un producto de orbitales atómicos similares al hidrógeno más simples. La periodicidad repetitiva de bloques de 2, 6, 10 y 14 elementos dentro de las secciones de la tabla periódica surge naturalmente del número total de electrones que ocupan un conjunto completo de orbitales s, p, d y f, respectivamente, aunque para mayores valores del número cuántico n, particularmente cuando el átomo tiene una carga positiva, las energías de ciertas subcapas se vuelven muy similares y, por lo tanto, el orden en que se dice que están pobladas por electrones (por ejemplo, Cr = [Ar] 4s 3d y Cr = [Ar] 3d) solo puede racionalizarse de manera un tanto arbitraria.

Propiedades de los electrones

Con el desarrollo de la mecánica cuántica y los hallazgos experimentales (como la difracción de electrones en dos rendijas), se descubrió que los electrones que orbitan alrededor de un núcleo no podían describirse completamente como partículas, sino que debían explicarse por la dualidad onda-partícula. En este sentido, los electrones tienen las siguientes propiedades:

Propiedades ondulatorias:

Los electrones no orbitan alrededor de un núcleo a la manera de un planeta que orbita alrededor del Sol, sino que existen como ondas estacionarias. Por lo tanto, la energía más baja posible que puede tomar un electrón es similar a la frecuencia fundamental de una onda en una cuerda. Los estados de mayor energía son similares a los armónicos de esa frecuencia fundamental.
Los electrones nunca están en una ubicación de un solo punto, aunque la probabilidad de interactuar con el electrón en un solo punto se puede encontrar a partir de la función de onda del electrón. La carga del electrón actúa como si estuviera esparcida en el espacio en una distribución continua, proporcional en cualquier punto al cuadrado de la magnitud de la función de onda del electrón.

Propiedades de partículas:

El número de electrones que orbitan alrededor de un núcleo solo puede ser un número entero.
Los electrones saltan entre orbitales como partículas. Por ejemplo, si un fotón golpea a los electrones, como resultado solo un electrón cambia de estado.
Los electrones conservan propiedades similares a las de las partículas, tales como: cada estado de onda tiene la misma carga eléctrica que su partícula electrónica. Cada estado de onda tiene un único giro discreto (girar hacia arriba o hacia abajo) dependiendo de su superposición.

Por lo tanto, los electrones no pueden describirse simplemente como partículas sólidas. Una analogía podría ser la de una "atmósfera" grande y, a menudo, de forma extraña (el electrón), distribuida alrededor de un planeta relativamente pequeño (el núcleo). Los orbitales atómicos describen exactamente la forma de esta "atmósfera" solo cuando está presente un electrón. Cuando se agregan más electrones, los electrones adicionales tienden a llenar más uniformemente un volumen de espacio alrededor del núcleo, de modo que la colección resultante ("nube de electrones") tiende hacia una zona de probabilidad generalmente esférica que describe la ubicación del electrón, debido a la incertidumbre. principio.

Definición mecánica cuántica formal

Los orbitales atómicos pueden definirse con mayor precisión en el lenguaje mecánico cuántico formal. Son soluciones aproximadas a la ecuación de Schrödinger para los electrones unidos al átomo por el campo eléctrico del núcleo del átomo. Específicamente, en la mecánica cuántica, el estado de un átomo, es decir, un estado propio del hamiltoniano atómico, se aproxima mediante una expansión (consulte la expansión de la interacción de configuración y el conjunto de bases) en combinaciones lineales de productos antisimetrizados (determinantes de Slater) de uno. funciones electrónicas. Los componentes espaciales de estas funciones de un electrón se denominan orbitales atómicos. (Cuando se considera también su componente de espín, se habla de orbitales atómicos de espín.) Un estado es en realidad una función de las coordenadas de todos los electrones, por lo que su movimiento está correlacionado, pero esto a menudo se aproxima mediante este modelo de partículas independientes de productos de funciones de onda de un solo electrón. (La fuerza de dispersión de London, por ejemplo, depende de las correlaciones del movimiento de los electrones).

En física atómica, las líneas espectrales atómicas corresponden a transiciones (saltos cuánticos) entre estados cuánticos de un átomo. Estos estados están etiquetados por un conjunto de números cuánticos resumidos en el término símbolo y generalmente asociados con configuraciones electrónicas particulares, es decir, por esquemas de ocupación de orbitales atómicos (por ejemplo, 1s 2s 2p para el estado fundamental del símbolo del término neón: S ₀).

Esta notación significa que los determinantes de Slater correspondientes tienen un peso claramente mayor en la expansión de la interacción de configuración. El concepto de orbital atómico es, por lo tanto, un concepto clave para visualizar el proceso de excitación asociado con una transición dada. Por ejemplo, se puede decir para una transición dada que corresponde a la excitación de un electrón de un orbital ocupado a un orbital desocupado dado. Sin embargo, hay que tener en cuenta que los electrones son fermiones regidos por el principio de exclusión de Pauli y no se pueden distinguir entre sí. Además, a veces sucede que la expansión de la interacción de configuración converge muy lentamente y que no se puede hablar en absoluto de una función de onda simple de un determinante. Este es el caso cuando la correlación de electrones es grande.

Fundamentalmente, un orbital atómico es una función de onda de un electrón, aunque muchos electrones no están en átomos de un electrón, por lo que la vista de un electrón es una aproximación. Cuando pensamos en orbitales, a menudo se nos ofrece una visualización de orbitales fuertemente influenciada por la aproximación de Hartree-Fock, que es una forma de reducir las complejidades de la teoría de orbitales moleculares.

Tipos de orbitales

Los orbitales atómicos pueden ser "orbitales" similares al hidrógeno, que son soluciones exactas de la ecuación de Schrödinger para un "átomo" similar al hidrógeno (es decir, un átomo con un electrón). Alternativamente, los orbitales atómicos se refieren a funciones que dependen de las coordenadas de un electrón (es decir, orbitales) pero se usan como puntos de partida para aproximar funciones de onda que dependen de las coordenadas simultáneas de todos los electrones en un átomo o molécula. Los sistemas de coordenadas elegidos para los orbitales suelen ser coordenadas esféricas (r, θ, φ) en átomos y cartesianas (x, y, z)en moléculas poliatómicas. La ventaja de las coordenadas esféricas aquí es que una función de onda orbital es un producto de tres factores, cada uno de los cuales depende de una sola coordenada: ψ (r, θ, φ) = R (r) Θ(θ) Φ(φ). Los factores angulares de los orbitales atómicos Θ(θ) Φ(φ) generan funciones s, p, d, etc. como combinaciones reales de armónicos esféricos Y _ℓm (θ, φ) (donde ℓ y mson números cuánticos). Por lo general, existen tres formas matemáticas para las funciones radiales R (r) que se pueden elegir como punto de partida para el cálculo de las propiedades de los átomos y moléculas con muchos electrones:

Los orbitales similares al hidrógeno se derivan de las soluciones exactas de la ecuación de Schrödinger para un electrón y un núcleo, para un átomo similar al hidrógeno. La parte de la función que depende de la distancia r del núcleo tiene nodos radiales y decae como e.
El orbital de tipo Slater (STO) es una forma sin nodos radiales pero se desintegra desde el núcleo al igual que un orbital similar al hidrógeno.
La forma del orbital de tipo gaussiano (gaussianos) no tiene nodos radiales y decae como ${displaystyle e^{-alpha r^{2}}}$ .

Aunque los orbitales similares al hidrógeno todavía se usan como herramientas pedagógicas, la llegada de las computadoras ha hecho que los STO sean preferibles para los átomos y las moléculas diatómicas, ya que las combinaciones de STO pueden reemplazar los nodos en los orbitales similares al hidrógeno. Los gaussianos se utilizan típicamente en moléculas con tres o más átomos. Aunque no son tan precisos por sí mismos como los STO, las combinaciones de muchos gaussianos pueden alcanzar la precisión de los orbitales similares al hidrógeno.

Historia

El término "orbital" fue acuñado por Robert Mulliken en 1932 como abreviatura de función de onda orbital de un electrón. Niels Bohr explicó alrededor de 1913 que los electrones podrían girar alrededor de un núcleo compacto con un momento angular definido. El modelo de Bohr fue una mejora de las explicaciones de 1911 de Ernest Rutherford, la del electrón moviéndose alrededor de un núcleo. El físico japonés Hantaro Nagaoka publicó una hipótesis basada en la órbita para el comportamiento de los electrones ya en 1904. Cada una de estas teorías se basó en nuevas observaciones que comenzaron con una comprensión simple y se volvieron más correctas y complejas. Explicar el comportamiento de estas "órbitas" de electrones fue una de las fuerzas impulsoras detrás del desarrollo de la mecánica cuántica.

Primeros modelos

Con el descubrimiento del electrón por JJ Thomson en 1897, quedó claro que los átomos no eran los bloques de construcción más pequeños de la naturaleza, sino partículas compuestas. La estructura recién descubierta dentro de los átomos tentó a muchos a imaginar cómo las partes constituyentes del átomo podrían interactuar entre sí. Thomson teorizó que múltiples electrones giran en anillos similares a órbitas dentro de una sustancia gelatinosa cargada positivamente, y entre el descubrimiento del electrón y 1909, este "modelo de pudín de ciruelas" fue la explicación más aceptada de la estructura atómica.

Poco después del descubrimiento de Thomson, Hantaro Nagaoka predijo un modelo diferente para la estructura electrónica. A diferencia del modelo de pudín de ciruelas, la carga positiva en el "Modelo de Saturno" de Nagaoka se concentró en un núcleo central, atrayendo los electrones en órbitas circulares que recuerdan a los anillos de Saturno. Pocas personas se dieron cuenta del trabajo de Nagaoka en ese momento, y el propio Nagaoka reconoció un defecto fundamental en la teoría, incluso en su concepción, a saber, que un objeto cargado clásico no puede mantener el movimiento orbital porque está acelerando y, por lo tanto, pierde energía debido a la radiación electromagnética. No obstante, el modelo de Saturno resultó tener más en común con la teoría moderna que cualquiera de sus contemporáneos.

átomo de bohr

En 1909, Ernest Rutherford descubrió que la mayor parte de la masa atómica estaba fuertemente condensada en un núcleo, que también estaba cargado positivamente. Quedó claro a partir de su análisis en 1911 que el modelo del pudín de ciruelas no podía explicar la estructura atómica. En 1913, el estudiante de posdoctorado de Rutherford, Niels Bohr, propuso un nuevo modelo del átomo, en el que los electrones orbitaban el núcleo con períodos clásicos, pero solo se les permitía tener valores discretos de momento angular, cuantificados en unidades ħ. Esta restricción permitía automáticamente solo ciertas energías de electrones. El modelo de Bohr del átomo solucionó el problema de la pérdida de energía por la radiación de un estado fundamental (al declarar que no había ningún estado debajo de este) y, lo que es más importante, explicó el origen de las líneas espectrales.

Después de que Bohr usara la explicación de Einstein del efecto fotoeléctrico para relacionar los niveles de energía en los átomos con la longitud de onda de la luz emitida, la conexión entre la estructura de los electrones en los átomos y los espectros de emisión y absorción de los átomos se convirtió en una herramienta cada vez más útil en la comprensión de los electrones. en átomos La característica más destacada de los espectros de emisión y absorción (conocidos experimentalmente desde mediados del siglo XIX) era que estos espectros atómicos contenían líneas discretas. La importancia del modelo de Bohr era que relacionaba las líneas en los espectros de emisión y absorción con las diferencias de energía entre las órbitas que los electrones podían tomar alrededor de un átomo. Sin embargo, esto no fuelogrado por Bohr al dar a los electrones algún tipo de propiedades ondulatorias, ya que la idea de que los electrones podrían comportarse como ondas de materia no se sugirió hasta once años después. Aún así, el uso del modelo de Bohr de momentos angulares cuantificados y, por lo tanto, niveles de energía cuantificados fue un paso significativo hacia la comprensión de los electrones en los átomos, y también un paso significativo hacia el desarrollo de la mecánica cuántica al sugerir que las restricciones cuantificadas deben tener en cuenta todos los niveles de energía discontinuos. y espectros en átomos.

Con la sugerencia de de Broglie de la existencia de ondas de materia de electrones en 1924, y durante un corto tiempo antes del tratamiento completo de la ecuación de Schrödinger de 1926 de los átomos similares al hidrógeno, se podía ver que la "longitud de onda" de un electrón de Bohr era una función de su impulso; por lo tanto, se vio que un electrón en órbita de Bohr orbitaba en un círculo en un múltiplo de su media longitud de onda.El modelo de Bohr por un corto tiempo podría verse como un modelo clásico con una restricción adicional proporcionada por el argumento de la 'longitud de onda'. Sin embargo, este período fue reemplazado inmediatamente por la mecánica ondulatoria tridimensional completa de 1926. En nuestra comprensión actual de la física, el modelo de Bohr se denomina modelo semiclásico debido a su cuantización del momento angular, no principalmente a causa de su relación con longitud de onda del electrón, que apareció en retrospectiva una docena de años después de que se propusiera el modelo de Bohr.

El modelo de Bohr fue capaz de explicar los espectros de emisión y absorción del hidrógeno. Las energías de los electrones en los estados n = 1, 2, 3, etc. del modelo de Bohr coinciden con las de la física actual. Sin embargo, esto no explicaba las similitudes entre diferentes átomos, tal como se expresa en la tabla periódica, como el hecho de que el helio (dos electrones), el neón (10 electrones) y el argón (18 electrones) exhiben una inercia química similar. La mecánica cuántica moderna explica esto en términos de capas y subcapas de electrones, cada una de las cuales puede contener una cantidad de electrones determinada por el principio de exclusión de Pauli. Por lo tanto, el estado n = 1 puede contener uno o dos electrones, mientras que el estado n = 2 puede contener hasta ocho electrones en las subcapas 2s y 2p. En helio, todo n = 1 estados están completamente ocupados; lo mismo es cierto para n = 1 y n = 2 en neón. En el argón, las subcapas 3s y 3p están completamente ocupadas de manera similar por ocho electrones; la mecánica cuántica también permite una subcapa 3d, pero esta tiene una energía más alta que las 3s y 3p en argón (al contrario de la situación del hidrógeno) y permanece vacía.

Concepciones modernas y conexiones con el principio de incertidumbre de Heisenberg

Inmediatamente después de que Heisenberg descubriera su principio de incertidumbre, Bohr notó que la existencia de cualquier tipo de paquete de ondas implica incertidumbre en la frecuencia y longitud de onda de la onda, ya que se necesita una dispersión de frecuencias para crear el paquete en sí.En la mecánica cuántica, donde todos los momentos de las partículas están asociados con ondas, es la formación de dicho paquete de ondas lo que localiza la onda, y por lo tanto la partícula, en el espacio. En los estados en los que una partícula mecánica cuántica está unida, debe localizarse como un paquete de ondas, y la existencia del paquete y su tamaño mínimo implica una dispersión y un valor mínimo en la longitud de onda de la partícula y, por lo tanto, también en el impulso y la energía. En la mecánica cuántica, a medida que una partícula se localiza en una región más pequeña del espacio, el paquete de ondas comprimido asociado requiere un rango de momentos cada vez mayor y, por lo tanto, una energía cinética mayor. Por lo tanto, la energía de enlace para contener o atrapar una partícula en una región más pequeña del espacio aumenta sin límites a medida que la región del espacio se hace más pequeña. Las partículas no pueden restringirse a un punto geométrico en el espacio,

En química, Schrödinger, Pauling, Mulliken y otros señalaron que la consecuencia de la relación de Heisenberg era que no se podía considerar que el electrón, como paquete de ondas, tuviera una ubicación exacta en su orbital. Max Born sugirió que la posición del electrón debía describirse mediante una distribución de probabilidad que estuviera relacionada con encontrar el electrón en algún punto de la función de onda que describía su paquete de ondas asociado. La nueva mecánica cuántica no dio resultados exactos, sino sólo las probabilidades de que se produjera una variedad de tales resultados posibles. Heisenberg sostuvo que la trayectoria de una partícula en movimiento no tiene sentido si no podemos observarla, como no podemos con los electrones en un átomo.

En la imagen cuántica de Heisenberg, Schrödinger y otros, el número de átomo de Bohr n para cada orbital se conocía como una esfera n en un átomo tridimensional y se representaba como la energía más probable de la nube de probabilidad del paquete de ondas del electrón que rodeaba el átomo.

Nombres orbitales

Notación orbital y subcapas

A los orbitales se les han dado nombres, que generalmente se dan en la forma: ${displaystyle X,mathrm {tipo} }$

donde X es el nivel de energía correspondiente al número cuántico principal n; tipo es una letra minúscula que denota la forma o subcapa del orbital, correspondiente al número cuántico de momento angular ℓ.

Por ejemplo, el orbital 1s (pronunciado como números y letras individuales: "'uno' 'ess'") es el nivel de energía más bajo (n = 1) y tiene un número cuántico angular de ℓ = 0, denotado como s. Los orbitales con ℓ = 1, 2 y 3 se denotan como p, d y f respectivamente.

El conjunto de orbitales para un n y ℓ dados se denomina subcapa, denotada $X,mathrm {tipo} ^{y}$ .

El exponente y muestra el número de electrones en la subcapa. Por ejemplo, la notación 2p indica que la subcapa 2p de un átomo contiene 4 electrones. Esta subcapa tiene 3 orbitales, cada uno con n = 2 y ℓ = 1.

Notación de rayos X

También hay otro sistema menos común que todavía se usa en la ciencia de rayos X conocido como notación de rayos X, que es una continuación de las notaciones utilizadas antes de que se entendiera bien la teoría orbital. En este sistema, al número cuántico principal se le asigna una letra asociada. Para n = 1, 2, 3, 4, 5,..., las letras asociadas a esos números son K, L, M, N, O,... respectivamente.

Orbitales similares al hidrógeno

Los orbitales atómicos más simples son los que se calculan para sistemas con un solo electrón, como el átomo de hidrógeno. Un átomo de cualquier otro elemento ionizado hasta un solo electrón es muy similar al hidrógeno y los orbitales toman la misma forma. En la ecuación de Schrödinger para este sistema de una partícula negativa y una positiva, los orbitales atómicos son los estados propios del operador hamiltoniano para la energía. Se pueden obtener analíticamente, lo que significa que los orbitales resultantes son productos de una serie polinomial y funciones exponenciales y trigonométricas. (ver átomo de hidrógeno).

Para átomos con dos o más electrones, las ecuaciones gobernantes solo pueden resolverse con el uso de métodos de aproximación iterativa. Los orbitales de los átomos multielectrónicos son cualitativamente similares a los del hidrógeno y, en los modelos más simples, se supone que tienen la misma forma. Para un análisis más riguroso y preciso, se deben utilizar aproximaciones numéricas.

Un orbital atómico dado (similar al hidrógeno) se identifica mediante valores únicos de tres números cuánticos: n, ℓ y m _ℓ. Las reglas que restringen los valores de los números cuánticos y sus energías (ver más abajo), explican la configuración electrónica de los átomos y la tabla periódica.

Los estados estacionarios (estados cuánticos) de los átomos similares al hidrógeno son sus orbitales atómicos. Sin embargo, en general, el comportamiento de un electrón no está completamente descrito por un solo orbital. Los estados electrónicos se representan mejor mediante "mezclas" (combinaciones lineales) dependientes del tiempo de múltiples orbitales. Ver Combinación lineal de orbitales atómicos Método de orbitales moleculares.

El número cuántico n apareció por primera vez en el modelo de Bohr, donde determina el radio de cada órbita circular de electrones. Sin embargo, en la mecánica cuántica moderna, n determina la distancia media del electrón al núcleo; todos los electrones con el mismo valor de n se encuentran a la misma distancia promedio. Por esta razón, se dice que los orbitales con el mismo valor de n forman una "cáscara". Los orbitales con el mismo valor de n y también el mismo valor de ℓ están aún más estrechamente relacionados y se dice que comprenden una "subcapa".

Números cuánticos

Debido a la naturaleza mecánica cuántica de los electrones alrededor de un núcleo, los orbitales atómicos se pueden definir de manera única mediante un conjunto de números enteros conocidos como números cuánticos. Estos números cuánticos solo ocurren en ciertas combinaciones de valores, y su interpretación física cambia dependiendo de si se emplean versiones reales o complejas de los orbitales atómicos.

Orbitales complejos

En física, las descripciones de orbitales más comunes se basan en las soluciones del átomo de hidrógeno, donde los orbitales vienen dados por el producto entre una función radial y un armónico esférico puro. Los números cuánticos, junto con las reglas que rigen sus posibles valores, son los siguientes:

El número cuántico principal n describe la energía del electrón y siempre es un número entero positivo. De hecho, puede ser cualquier número entero positivo, pero por las razones que se analizan a continuación, rara vez se encuentran números grandes. Cada átomo tiene, en general, muchos orbitales asociados con cada valor de n; estos orbitales juntos a veces se denominan capas de electrones.

El número cuántico azimutal ℓ describe el momento angular orbital de cada electrón y es un número entero no negativo. Dentro de un caparazón donde n es un número entero n ₀, ℓ abarca todos los valores (enteros) que satisfacen la relación $0leqellleq n_{0}-1$ . Por ejemplo, la capa n = 1 solo tiene orbitales con $ell =0$ , y la capa n = 2 solo tiene orbitales con $ell =0$ , y $ell =1$ . El conjunto de orbitales asociados con un valor particular de ℓ a veces se denominan colectivamente subcapa.

El número cuántico magnético, $m_{ell}$ , describe el momento magnético de un electrón en una dirección arbitraria y también es siempre un número entero. Dentro de una subcapa donde $ana$ hay algún número entero $ell _{0}$ , $m_{ell}$ varía así: $-ell_{0}leq m_{ell }leq ell_{0}$ .

Los resultados anteriores pueden resumirse en la siguiente tabla. Cada celda representa una subcapa y enumera los valores $m_{ell}$ disponibles en esa subcapa. Las celdas vacías representan subcapas que no existen.

	ℓ = 0 (segundos)	ℓ = 1 (p)	ℓ = 2 (d)	ℓ = 3 (h)	ℓ = 4 (gramos)	...
norte = 1	$m_{ell}=0$					...
norte = 2	0	−1, 0, 1				...
norte = 3	0	−1, 0, 1	−2, −1, 0, 1, 2			...
norte = 4	0	−1, 0, 1	−2, −1, 0, 1, 2	−3, −2, −1, 0, 1, 2, 3		...
norte = 5	0	−1, 0, 1	−2, −1, 0, 1, 2	−3, −2, −1, 0, 1, 2, 3	−4, −3, −2, −1, 0, 1, 2, 3, 4	...
...	...	...	...	...	...	...

Las subcapas generalmente se identifican por sus valores $norte$ - y - $ana$ . $norte$ está representado por su valor numérico, pero $ana$ está representado por una letra de la siguiente manera: 0 está representado por 's', 1 por 'p', 2 por 'd', 3 por 'f' y 4 por 'g'. Por ejemplo, se puede hablar del subnivel con $n=2$ y $ell =0$ como un 'subnivel 2s'.

Cada electrón también tiene un número cuántico de espín, s, que describe el espín de cada electrón (espín hacia arriba o hacia abajo). El número s puede ser +1/2o -1/2.

El principio de exclusión de Pauli establece que dos electrones en un átomo no pueden tener los mismos valores de los cuatro números cuánticos. Si hay dos electrones en un orbital con valores dados para tres números cuánticos (n, ℓ, m), estos dos electrones deben diferir en su espín.

Las convenciones anteriores implican un eje preferido (por ejemplo, la dirección z en coordenadas cartesianas), y también implican una dirección preferida a lo largo de este eje preferido. De lo contrario, no tendría sentido distinguir m = +1 de m = −1. Como tal, el modelo es más útil cuando se aplica a sistemas físicos que comparten estas simetrías. El experimento de Stern-Gerlach, en el que se expone un átomo a un campo magnético, proporciona uno de esos ejemplos.

Orbitales reales

Además de los orbitales complejos descritos anteriormente, es común, especialmente en la literatura química, utilizar orbitales atómicos reales. Estos orbitales reales surgen de combinaciones lineales simples de orbitales complejos. Usando la convención de fase de Condon-Shortley, los orbitales reales se relacionan con los orbitales complejos de la misma manera que los armónicos esféricos reales se relacionan con los armónicos esféricos complejos. Dejando ${ estilo de visualización psi _ {n, ell, m}}$ denotar un orbital complejo con números cuánticos $norte$ , $yo$ y $metro$ , los orbitales reales ${displaystyle psi _{n,ell,m}^{text{real}}}$ pueden definirse por ${displaystyle psi _{n,ell,m}^{text{real}}={begin{casos}{sqrt {2}}(-1)^{m}{text{Im} }left{psi _{n,ell,|m|}right}&{text{ for }}m<0\psi _{n,ell,|m|}&{ text{ para }}m=0\{sqrt {2}}(-1)^{m}{text{Re}}left{psi _{n,ell,|m|} right}&{text{ para }}m>0end{casos}}={begin{casos}{frac {i}{sqrt {2}}}left(psi _{n,ell,-|m|}-(-1)^{m}psi _{n,ell,|m|}right)&{text{ para }}m<0\psi _ {n,ell,|m|}&{text{ para }}m=0\{frac {1}{sqrt {2}}}left(psi _{n,ell,- |m|}+(-1)^{m}psi _{n,ell,|m|}right)&{text{ para }}m<0\end{casos}}}$

Si ${displaystyle psi _{n,ell,m}(r,theta,phi)=R_{nl}(r)Y_{ell }^{m}(theta,phi)}$ , con $R_{{nl}}(r)$ la parte radial del orbital, esta definición es equivalente a ${displaystyle psi _{n,ell,m}^{text{real}}(r,theta,phi)=R_{nl}(r)Y_{ell m}(theta, fi)}$ donde $Y_{ell m}$ está el armónico esférico real relacionado con la parte real o imaginaria del armónico esférico complejo $Y_{ell}^m$ .

Los armónicos esféricos reales son físicamente relevantes cuando un átomo está incrustado en un sólido cristalino, en cuyo caso hay múltiples ejes de simetría preferidos pero ninguna dirección preferida única. Los orbitales atómicos reales también se encuentran con mayor frecuencia en los libros de texto de introducción a la química y se muestran en visualizaciones orbitales comunes. En los orbitales reales similares al hidrógeno, los números cuánticos tienen la misma interpretación y significado que sus contrapartes complejas, pero $norte$ ya no es un buen número cuántico (pero su valor absoluto sí lo es). $ana$ $metro$

Algunos orbitales reales reciben nombres específicos más allá de la simple ${ estilo de visualización psi _ {n, ell, m}}$ designación. Los orbitales con número cuántico $ana$ igual a ${displaystyle 0,1,2,3,4,5,6ldots}$ se llaman ${displaystyle s,p,d,f,g,h,ldots}$ orbitales. Con esto ya se pueden asignar nombres a orbitales complejos como ${displaystyle 2p_{pm 1}=psi _{2,1,pm 1}}$ ; el primer símbolo es el $norte$ número cuántico, el segundo número es el símbolo de ese $ana$ número cuántico particular y el subíndice es el $metro$ número cuántico.

Como ejemplo de cómo se generan los nombres orbitales completos para orbitales reales, se puede calcular ${displaystyle psi _{n,1,pm 1}^{text{real}}}$ . De la tabla de armónicos esféricos, ${displaystyle psi _{n,1,pm 1}=R_{n,1}Y_{1}^{pm 1}=mp R_{n,1}{sqrt {3/8pi }}cdot (xpm iy)/r}$ con ${displaystyle r={sqrt {x^{2}+y^{2}+z^{2}}}}$ . Después ${displaystyle {begin{alineado}psi _{n,1,+1}^{text{real}}=&R_{n,1}{sqrt {frac {3}{4pi }} }cdot {frac {x}{r}}\psi _{n,1,-1}^{text{real}}=&R_{n,1}{sqrt {frac {3} {4pi }}}cdot {frac {y}{r}}end{alineado}}}$

Del mismo modo ${displaystyle psi _{n,1,0}=R_{n,1}{sqrt {3/4pi }}cdot z/r}$ . Como un ejemplo más complicado: ${displaystyle psi _{n,3,+1}^{text{real}}=R_{n,3}{frac {1}{4}}{sqrt {frac {21}{2 pi }}}cdot {frac {xcdot (5z^{2}-r^{2})}{r^{3}}}}$

En todos estos casos, generamos una etiqueta cartesiana para el orbital examinando y abreviando el polinomio en $X$ , $y$ y $z$ apareciendo en el numerador. Ignoramos cualquier término en el ${ estilo de visualización z, r}$ polinomio excepto el término con el exponente más alto en $z$ . Luego usamos el polinomio abreviado como una etiqueta de subíndice para el estado atómico, usando la misma nomenclatura que arriba para indicar los números cuánticos $norte$ y. $ana$ ${displaystyle {begin{alineado}psi _{n,1,-1}^{text{real}}=&np_{y}={frac {i}{sqrt {2}}}left (np_{-1}+np_{+1}right)\psi _{n,1,0}^{text{real}}=&np_{z}=2p_{0}\psi _ {n,1,+1}^{text{real}}=&np_{x}={frac {1}{sqrt {2}}}left(np_{-1}-np_{+1} right)\psi _{n,3,+1}^{text{real}}=&nf_{xz^{2}}={frac {1}{sqrt {2}}}left (nf_{-1}-nf_{+1}right)end{alineado}}}$

La expresión sobre todo utiliza la convención de fase de Condon-Shortley que es favorecida por los físicos cuánticos. Existen otras convenciones para la fase de los armónicos esféricos. Bajo estas diferentes convenciones, los orbitales $p_{x}$ y $p_{y}$ pueden aparecer, por ejemplo, como la suma y la diferencia de ${displaystyle p_{+1}}$ y ${displaystyle p_{-1}}$ , al contrario de lo que se muestra arriba.

A continuación se muestra una lista de estos nombres de polinomios cartesianos para los orbitales atómicos. Tenga en cuenta que no parece haber referencia en la literatura sobre cómo abreviar los polinomios armónicos esféricos cartesianos largos, por ${ estilo de visualización ell > 3}$ lo que no parece haber consenso sobre la denominación de $gramo$ orbitales o superiores de acuerdo con esta nomenclatura.

	metro = −3	metro = −2	metro = −1	metro = 0	metro = +1	metro = +2	metro = +3
$ell =0$				$s$
$ell =1$			$p_{y}$	$p_{z}$	$p_{x}$
$ell =2$		${ estilo de visualización d_ {xy}}$	$d_{{yz}}$	$d_{{z^{2}}}$	$d_{{xz}}$	${displaystyle d_{x^{2}-y^{2}}}$
${ estilo de visualización ell = 3}$	${displaystyle f_{y(3x^{2}-y^{2})}}$	${displaystyle f_{xyz}}$	$f_{{yz^{2}}}$	$f_{{z^{3}}}$	$f_{{xz^{2}}}$	${displaystyle f_{z(x^{2}-y^{2})}}$	${displaystyle f_{x(x^{2}-3y^{2})}}$

Formas de orbitales

Las imágenes simples que muestran las formas de los orbitales pretenden describir las formas angulares de las regiones del espacio donde es probable que se encuentren los electrones que ocupan el orbital. Los diagramas no pueden mostrar toda la región donde se puede encontrar un electrón, ya que según la mecánica cuántica existe una probabilidad distinta de cero de encontrar el electrón (casi) en cualquier parte del espacio. En cambio, los diagramas son representaciones aproximadas de superficies límite o de contorno donde la densidad de probabilidad | ψ(r, θ, φ) | tiene un valor constante, elegido de modo que exista una cierta probabilidad (por ejemplo, 90%) de encontrar el electrón dentro del contorno. Aunque | ψ |como el cuadrado de un valor absoluto es no negativo en todas partes, el signo de la función de onda ψ(r, θ, φ) a menudo se indica en cada subregión de la imagen orbital.

A veces, la función ψ se representa gráficamente para mostrar sus fases, en lugar de | ψ(r, θ, φ) | que muestra densidad de probabilidad pero no tiene fase (que se pierde al tomar valor absoluto, ya que ψ(r, θ, φ) es un número complejo). | ψ(r, θ, φ) | los gráficos orbitales tienden a tener lóbulos menos esféricos y más delgados que ψ(r, θ, φ)gráficos, pero tienen el mismo número de lóbulos en los mismos lugares, y por lo demás son reconocibles. Este artículo, para mostrar la fase de la función de onda, muestra principalmente gráficos ψ(r, θ, φ).

Los lóbulos pueden verse como patrones de interferencia de ondas estacionarias entre los dos modos m y - m de ondas viajeras resonantes anulares contrarrotatorias; la proyección del orbital sobre el plano xy tiene una longitud de onda resonante m alrededor de la circunferencia. Aunque rara vez se muestran, las soluciones de ondas viajeras se pueden ver como toros con bandas giratorias; las bandas representan información de fase. Para cada m hay dos soluciones de onda estacionaria ⟨ m ⟩ + ⟨− m ⟩ y ⟨ m ⟩ − ⟨− m ⟩. Si m = 0, el orbital es vertical, se desconoce la información contrarrotante y el orbital es simétrico en el eje z. Si ℓ = 0 no hay modos de rotación contraria. Solo hay modos radiales y la forma es esféricamente simétrica. Para cualquier n dado, cuanto menor es ℓ, más nodos radiales hay. Para cualquier ℓ dado, cuanto menor es n, menos nodos radiales hay (cero para el n que primero tenga ese orbital ℓ). En términos generales, n es energía, ℓ es análogo a la excentricidad y mes orientación. En el caso clásico, una onda viajera resonante en anillo, por ejemplo en una línea de transmisión circular, a menos que se fuerce activamente, decae espontáneamente en una onda estacionaria resonante en anillo porque las reflexiones se acumulan con el tiempo incluso en la más pequeña imperfección o discontinuidad.

En general, n determina el tamaño y la energía del orbital para un núcleo dado; a medida que n aumenta, el tamaño del orbital aumenta. La mayor carga nuclear Z de los elementos más pesados hace que sus orbitales se contraigan en comparación con los más ligeros, de modo que el tamaño del átomo permanece aproximadamente constante, incluso cuando aumenta el número de electrones.

También en términos generales, ℓ determina la forma de un orbital y m _ℓ su orientación. Sin embargo, dado que algunos orbitales se describen mediante ecuaciones en números complejos, la forma a veces también depende de m _ℓ. Juntos, el conjunto completo de orbitales para un ℓ y n dados llenan el espacio de la manera más simétrica posible, aunque con conjuntos de lóbulos y nodos cada vez más complejos.

Los orbitales s individuales ( $ell =0$ ) tienen forma de esferas. Para n = 1, es aproximadamente una bola sólida (más densa en el centro y se desvanece hacia afuera exponencialmente), pero para n ≥ 2, cada orbital s está hecho de superficies esféricamente simétricas que son capas anidadas (es decir, la "estructura de onda" es radial, siguiendo también una componente radial sinusoidal). Vea la ilustración de una sección transversal de estas conchas anidadas, a la derecha. Los orbitales s para todos los n números son los únicos orbitales con un antinodo (una región de alta densidad de función de onda) en el centro del núcleo. Todos los demás orbitales (p, d, f, etc.) tienen momento angular y, por lo tanto, evitan el núcleo (que tiene un nodo de onda enel núcleo). Recientemente, ha habido un esfuerzo para obtener imágenes experimentales de los orbitales 1s y 2p en un cristal de SrTiO ₃ utilizando microscopía electrónica de transmisión de barrido con espectroscopía de rayos X de dispersión de energía. Debido a que la imagen se realizó utilizando un haz de electrones, la interacción orbital-haz de Coulombic, que a menudo se denomina efecto del parámetro de impacto, se incluye en el resultado final (ver la figura a la derecha).

Las formas de los orbitales p, d y f se describen verbalmente aquí y se muestran gráficamente en la tabla de orbitales a continuación. Los tres orbitales p para n = 2 tienen la forma de dos elipsoides con un punto de tangencia en el núcleo (la forma de dos lóbulos a veces se denomina "pesa": hay dos lóbulos que apuntan en direcciones opuestas entre sí). Los tres orbitales p en cada capa están orientados en ángulo recto entre sí, según lo determinado por su respectiva combinación lineal de valores de m _ℓ. El resultado general es un lóbulo que apunta a lo largo de cada dirección de los ejes primarios.

Cuatro de los cinco orbitales d para n = 3 se ven similares, cada uno con cuatro lóbulos en forma de pera, cada lóbulo es tangente en ángulo recto a los otros dos, y los centros de los cuatro se encuentran en un plano. Tres de estos planos son los planos xy, xz e yz (los lóbulos están entre los pares de ejes primarios) y el cuarto tiene el centro a lo largo de los ejes x e y. El quinto y último orbital d consta de tres regiones de alta densidad de probabilidad: un toro entre dos regiones en forma de pera colocadas simétricamente en su eje z. El total general de 18 lóbulos direccionales apuntan en cada dirección del eje primario y entre cada par.

Hay siete orbitales f, cada uno con formas más complejas que las de los orbitales d.

Además, como en el caso de los orbitales s, los orbitales p, d, f y g individuales con valores n mayores que el valor más bajo posible, exhiben una estructura de nodo radial adicional que recuerda a las ondas armónicas del mismo tipo, en comparación con el modo más bajo (o fundamental) de la onda. Al igual que con los orbitales s, este fenómeno proporciona orbitales p, d, f y g en el siguiente valor más alto posible de n (por ejemplo, orbitales 3p frente al 2p fundamental), un nodo adicional en cada lóbulo. Valores aún más altos de n aumentan aún más el número de nodos radiales, para cada tipo de orbital.

Las formas de los orbitales atómicos en un átomo de un electrón están relacionadas con armónicos esféricos tridimensionales. Estas formas no son únicas, y cualquier combinación lineal es válida, como una transformación a armónicos cúbicos, de hecho, es posible generar conjuntos donde todas las d tienen la misma forma, al igual que p x _, p _y y p _z son la misma forma

Aunque la mayoría de las veces los orbitales individuales se muestran independientes entre sí, los orbitales coexisten alrededor del núcleo al mismo tiempo. Además, en 1927, Albrecht Unsöld demostró que si uno suma la densidad electrónica de todos los orbitales de un número cuántico azimutal particular ℓ de la misma capa n (por ejemplo, los tres orbitales 2p o los cinco orbitales 3d) donde cada orbital está ocupado por un electrón o cada uno está ocupado por un par de electrones, entonces desaparece toda dependencia angular; es decir, la densidad total resultante de todos los orbitales atómicos en esa subcapa (aquellos con el mismo ℓ) es esférica. Esto se conoce como el teorema de Unsöld.

Tabla de orbitales

Esta tabla muestra las funciones de onda similares al hidrógeno reales para todos los orbitales atómicos hasta 7s y, por lo tanto, cubre los orbitales ocupados en el estado fundamental de todos los elementos de la tabla periódica hasta el radio y algunos más. Los gráficos "ψ" se muestran con las fases de función de onda − y + mostradas en dos colores diferentes (arbitrariamente rojo y azul). El orbital p _z es el mismo que el orbital p ₀, pero p _x y p _y se forman tomando combinaciones lineales de los orbitales p ₊₁ y p ₋₁ (por lo que se enumeran bajo m = ±1etiqueta). Además, p ₊₁ y p ₋₁ no tienen la misma forma que p ₀, ya que son armónicos esféricos puros.

	s (ℓ = 0)	pag (ℓ = 1)	re (ℓ = 2)	f (ℓ = 3)
	metro = 0	metro = 0	metro = ±1	metro = 0	metro = ±1	metro = ±2	metro = 0	metro = ±1	metro = ±2	metro = ±3
	s	pz _{_}	px _{_}	py _{_}	dz _{_}	dxz _{_}	dyz _{_}	d _xy	re _{x - y}	fz _{_}	fxz _{_}	f _yz	fxyz _{_}	f _{z (x − y)}	f _{x (x −3 y)}	f _{y (3 x − y)}
norte = 1
norte = 2
norte = 3
norte = 4
norte = 5										...	...	...	...	...	...	...
norte = 6					... ‡	...	... ‡	...	... ‡	... *	... *	... *	... *	... *	... *	... *
n = 7		... †	... †	... †	... *	... *	... *	... *	... *	... *	... *	... *	... *	... *	... *	... *

* Aún no se han descubierto elementos con electrones 6f, 7d o 7f.

† Se han descubierto elementos con electrones 7p, pero sus configuraciones electrónicas solo se predicen.

‡ Para los elementos cuyo orbital ocupado más alto es un orbital 6d, solo se han confirmado algunas configuraciones electrónicas. (Todavía faltan Ds, Rg y Cn).

Estos son los orbitales de valor real comúnmente utilizados en química. Solo los $metro=0$ orbitales donde son estados propios del operador de momento angular orbital, ${displaystyle {sombrero {L}}_{z}}$ . Las columnas con ${displaystyle m=pm 1,pm 2,cdots}$ son combinaciones de dos estados propios. Ver comparativa en la siguiente imagen:

Comprensión cualitativa de las formas.

Las formas de los orbitales atómicos pueden entenderse cualitativamente considerando el caso análogo de ondas estacionarias en un tambor circular.Para ver la analogía, el desplazamiento vibratorio medio de cada trozo de membrana del tambor desde el punto de equilibrio durante muchos ciclos (una medida de la velocidad y el momento promedio de la membrana del tambor en ese punto) debe considerarse en relación con la distancia de ese punto desde el centro del tambor. cabeza. Si este desplazamiento se toma como análogo a la probabilidad de encontrar un electrón a una distancia dada del núcleo, entonces se verá que los muchos modos del disco vibratorio forman patrones que trazan las diversas formas de los orbitales atómicos. La razón básica de esta correspondencia radica en el hecho de que la distribución de la energía cinética y el momento en una onda de materia predice dónde estará la partícula asociada con la onda. Es decir, la probabilidad de encontrar un electrón en un lugar dado también es función del electrón.

Esta relación significa que se pueden observar ciertas características clave tanto en los modos de membrana del tambor como en los orbitales atómicos. Por ejemplo, en todos los modos análogos a los orbitales s (la fila superior en la ilustración animada a continuación), se puede ver que el mismo centro de la membrana del tambor vibra más fuertemente, correspondiendo al antinodo en todos los orbitales s en un átomo.. Este antinodo significa que es más probable que el electrón esté en la posición física del núcleo (a través del cual pasa directamente sin dispersarse ni golpearlo), ya que se mueve (en promedio) más rápidamente en ese punto, lo que le otorga un impulso máximo.

Una imagen mental de "órbita planetaria" más cercana al comportamiento de los electrones en los orbitales s, todos los cuales no tienen momento angular, podría ser quizás la de una órbita kepleriana con la excentricidad orbital de 1 pero un eje mayor finito, no físicamente posible (porque las partículas colisionaran), pero se puede imaginar como un límite de órbitas con ejes mayores iguales pero excentricidad creciente.

A continuación, se muestran varios modos de vibración de la membrana del tambor y las respectivas funciones de onda del átomo de hidrógeno. Se puede considerar una correspondencia donde las funciones de onda de un parche de tambor vibrante son para un sistema de dos coordenadas ψ(r, θ) y las funciones de onda para una esfera vibrante son de tres coordenadas ψ(r, θ, φ).

modos de batería tipo s y funciones de onda
modo tambor $tu_{01}$
modo tambor $tu_{02}$
modo tambor $tu_{03}$
Función de onda del orbital 1s (parte real, corte 2D, ${displaystyle r_{máx}=2a_{0}}$ )
Función de onda del orbital 2s (parte real, corte 2D, ${displaystyle r_{máx}=10a_{0}}$ )
Función de onda del orbital 3s (parte real, corte 2D, ${displaystyle r_{máx}=20a_{0}}$ )

Ninguno de los otros conjuntos de modos en una membrana de tambor tiene un antinodo central y en todos ellos el centro del tambor no se mueve. Estos corresponden a un nodo en el núcleo para todos los orbitales no s en un átomo. Todos estos orbitales tienen algún momento angular y, en el modelo planetario, corresponden a partículas en órbita con una excentricidad inferior a 1,0, de modo que no pasan directamente por el centro del cuerpo primario, sino que se mantienen algo alejadas de él.

Además, los modos de tambor análogos a los modos p y d en un átomo muestran irregularidad espacial a lo largo de las diferentes direcciones radiales desde el centro del tambor, mientras que todos los modos análogos a los modos s son perfectamente simétricos en dirección radial. Las propiedades de simetría no radial de no- sLos orbitales son necesarios para localizar una partícula con momento angular y naturaleza ondulatoria en un orbital donde debe tender a alejarse de la fuerza de atracción central, ya que cualquier partícula localizada en el punto de atracción central podría no tener momento angular. Para estos modos, las ondas en el parche del tambor tienden a evitar el punto central. Tales características nuevamente enfatizan que las formas de los orbitales atómicos son una consecuencia directa de la naturaleza ondulatoria de los electrones.

modos de batería tipo p y funciones de onda
modo tambor $tu_{11}$
modo tambor $tu_{12}$
modo tambor $tu_{13}$
Función de onda del orbital 2p (parte real, corte 2D, ${displaystyle r_{máx}=10a_{0}}$ )
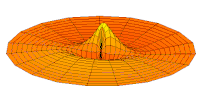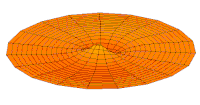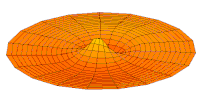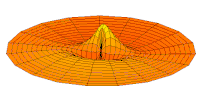Función de onda del orbital 3p (parte real, corte 2D, ${displaystyle r_{máx}=20a_{0}}$ )
Función de onda del orbital 4p (parte real, corte 2D, ${displaystyle r_{máx}=25a_{0}}$ )

modos de batería tipo d
modo tambor $tu_{21}$
modo tambor $tu_{22}$
modo tambor $tu_{23}$

Energía orbital

En átomos con un electrón (átomo similar al hidrógeno), la energía de un orbital (y, en consecuencia, cualquier electrón en el orbital) está determinada principalmente por $norte$ . El $n=1$ orbital tiene la energía más baja posible en el átomo. Cada valor sucesivamente más alto de $norte$ tiene una energía más alta, pero la diferencia disminuye a medida que $norte$ aumenta. Para alta $norte$ , la energía llega a ser tan alta que el electrón puede escapar fácilmente del átomo. En los átomos de un solo electrón, todos los niveles con diferentes $ana$ dentro de un dado $norte$ degeneran en la aproximación de Schrödinger y tienen la misma energía. Esta aproximación se rompe ligeramente en la solución de la ecuación de Dirac (donde la energía depende de n y de otro número cuántico j), y por el efecto del campo magnético del núcleo y efectos de la electrodinámica cuántica. Estos últimos inducen pequeñas diferencias de energía de enlace, especialmente para los electrones s que se acercan al núcleo, ya que estos sienten una carga nuclear muy ligeramente diferente, incluso en átomos de un electrón; ver Cambio de cordero.

En átomos con múltiples electrones, la energía de un electrón depende no solo de su orbital, sino también de sus interacciones con otros electrones. Estas interacciones dependen del detalle de su distribución de probabilidad espacial, por lo que los niveles de energía de los orbitales dependen no solo de $norte$ sino también de $ana$ . Los valores más altos de $ana$ están asociados con valores más altos de energía; por ejemplo, el estado 2p es más alto que el estado 2s. Cuando $ell =2$ , el aumento de energía del orbital se vuelve tan grande que empuja la energía del orbital por encima de la energía del orbital s en la siguiente capa más alta; cuando $ell =3$ la energía es empujada hacia el caparazón dos pasos más arriba. El llenado de los orbitales 3d no ocurre hasta que se hayan llenado los orbitales 4s.

El aumento en la energía de las subcapas de momento angular creciente en los átomos más grandes se debe a los efectos de la interacción electrón-electrón, y está específicamente relacionado con la capacidad de los electrones de momento angular bajo para penetrar más efectivamente hacia el núcleo, donde están sujetos a menos apantallamiento. de la carga de los electrones intermedios. Así, en átomos con mayor número atómico, el número $ana$ de electrones se vuelve cada vez más un factor determinante en su energía, y los principales números cuánticos $norte$ de electrones se vuelven cada vez menos importantes en su ubicación energética.

La secuencia de energía de las primeras 35 subcapas (por ejemplo, 1s, 2p, 3d, etc.) se da en la siguiente tabla. Cada celda representa una subcapa con $norte$ y $ana$ dada por sus índices de fila y columna, respectivamente. El número en la celda es la posición de la subcapa en la secuencia. Para obtener una lista lineal de las subcapas en términos de energías crecientes en átomos multielectrónicos, consulte la sección a continuación.

yonorte	s	pags	d	F	gramo	h
1	1
2	2	3
3	4	5	7
4	6	8	10	13
5	9	11	14	17	21
6	12	15	18	22	26	31
7	dieciséis	19	23	27	32	37
8	20	24	28	33	38	44
9	25	29	34	39	45	51
10	30	35	40	46	52	59

Nota: las celdas vacías indican subniveles inexistentes, mientras que los números en cursiva indican subniveles que podrían (potencialmente) existir, pero que no contienen electrones en ningún elemento actualmente conocido.

Colocación de electrones y la tabla periódica.

Varias reglas rigen la ubicación de los electrones en los orbitales (configuración electrónica). El primero dicta que dos electrones en un átomo no pueden tener el mismo conjunto de valores de números cuánticos (este es el principio de exclusión de Pauli). Estos números cuánticos incluyen los tres que definen los orbitales, así como el s, o número cuántico de espín. Por lo tanto, dos electrones pueden ocupar un solo orbital, siempre que tengan diferentes valores de s. Sin embargo, solo dos electrones, debido a su espín, pueden asociarse con cada orbital.

Además, un electrón siempre tiende a caer al estado de energía más bajo posible. Es posible que ocupe cualquier orbital siempre que no viole el principio de exclusión de Pauli, pero si se dispone de orbitales de menor energía, esta condición es inestable. El electrón finalmente perderá energía (al liberar un fotón) y caerá en el orbital inferior. Por lo tanto, los electrones llenan los orbitales en el orden especificado por la secuencia de energía dada anteriormente.

Este comportamiento es responsable de la estructura de la tabla periódica. La tabla se puede dividir en varias filas (llamadas 'períodos'), numeradas comenzando con 1 en la parte superior. Los elementos actualmente conocidos ocupan siete períodos. Si un período determinado tiene el número i, se compone de elementos cuyos electrones más externos caen en la i -ésima capa. Niels Bohr fue el primero en proponer (1923) que la periodicidad en las propiedades de los elementos podría explicarse por el llenado periódico de los niveles de energía de los electrones, dando como resultado la estructura electrónica del átomo.

La tabla periódica también se puede dividir en varios "bloques" rectangulares numerados. Los elementos que pertenecen a un bloque dado tienen esta característica común: sus electrones de mayor energía pertenecen todos al mismo estado ℓ (pero la n asociada con ese estado ℓ depende del período). Por ejemplo, las dos columnas más a la izquierda constituyen el 'bloque s'. Los electrones más externos de Li y Be pertenecen respectivamente a la subcapa 2s, y los de Na y Mg a la subcapa 3s.

El siguiente es el orden para llenar los orbitales de la "subcapa", que también da el orden de los "bloques" en la tabla periódica:1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p

La naturaleza "periódica" del llenado de los orbitales, así como la aparición de los "bloques" s, p, d y f, es más obvia si este orden de llenado se da en forma matricial, con números cuánticos principales crecientes comenzando el nuevas filas ("períodos") en la matriz. Luego, cada subcapa (compuesta por los dos primeros números cuánticos) se repite tantas veces como sea necesario por cada par de electrones que pueda contener. El resultado es una tabla periódica comprimida, en la que cada entrada representa dos elementos sucesivos:

Aunque este es el orden general de llenado orbital de acuerdo con la regla de Madelung, existen excepciones, y las energías electrónicas reales de cada elemento también dependen de detalles adicionales de los átomos (ver Configuración electrónica § Átomos: principio de Aufbau y regla de Madelung).

El número de electrones en un átomo eléctricamente neutro aumenta con el número atómico. Los electrones en la capa más externa, o electrones de valencia, tienden a ser responsables del comportamiento químico de un elemento. Los elementos que contienen el mismo número de electrones de valencia se pueden agrupar y mostrar propiedades químicas similares.

Efectos relativistas

Para elementos con alto número atómico Z, los efectos de la relatividad se vuelven más pronunciados, y especialmente para los electrones s, que se mueven a velocidades relativistas cuando penetran los electrones de apantallamiento cerca del núcleo de los átomos de alto Z. Este aumento relativista en el impulso de los electrones de alta velocidad provoca una disminución correspondiente en la longitud de onda y la contracción de los orbitales 6s en relación con los orbitales 5d (en comparación con los electrones s y d correspondientes en elementos más livianos en la misma columna de la tabla periódica); esto da como resultado que los electrones de valencia 6s pierdan energía.

Ejemplos de resultados físicos significativos de este efecto incluyen la temperatura de fusión más baja del mercurio (que resulta de que los electrones 6s no están disponibles para la unión de metales) y el color dorado del oro y el cesio.

En el modelo de Bohr, un electrón n = 1 tiene una velocidad dada por $v=Zalfa c$ , donde Z es el número atómico, $alfa$ es la constante de estructura fina y c es la velocidad de la luz. En la mecánica cuántica no relativista, por lo tanto, cualquier átomo con un número atómico mayor que 137 requeriría que sus electrones 1s viajaran más rápido que la velocidad de la luz. Incluso en la ecuación de Dirac, que explica los efectos relativistas, la función de onda del electrón para los átomos ${ estilo de visualización Z> 137}$ es oscilatoria e ilimitada. El significado del elemento 137, también conocido como untriseptium, fue señalado por primera vez por el físico Richard Feynman. El elemento 137 a veces se llama informalmente feynmanium (símbolo Fy).Sin embargo, la aproximación de Feynman no logra predecir el valor crítico exacto de Z debido a la naturaleza de carga no puntual del núcleo y al radio orbital muy pequeño de los electrones internos, lo que da como resultado un potencial visto por los electrones internos que es efectivamente menor que Z. El valor crítico de Z, que hace que el átomo sea inestable con respecto a la ruptura de alto campo del vacío y la producción de pares de electrones y positrones, no ocurre hasta que Z es de aproximadamente 173. Estas condiciones no se ven excepto de forma transitoria en colisiones de núcleos muy pesados. como el plomo o el uranio en aceleradores, donde se ha afirmado que se observa tal producción de electrones y positrones a partir de estos efectos.

No hay nodos en densidades orbitales relativistas, aunque los componentes individuales de la función de onda tendrán nodos.

Hibridación pp (conjeturada)

En los últimos 8 elementos del período, se espera que exista un híbrido de 8p _3/2 y 9p _1/2, donde "3/2" y "1/2" se refieren al número cuántico del momento angular total. Este híbrido "pp" puede ser responsable del bloque p del período debido a propiedades similares a las subcapas p en las capas de valencia ordinarias. Los niveles de energía de 8p _3/2 y 9p _1/2 se acercan debido a los efectos relativistas de giro-órbita; la subcapa 9s también debería participar, ya que se espera que estos elementos sean análogos a los respectivos elementos 5p de indio a xenón.

Transiciones entre orbitales

Los estados cuánticos ligados tienen niveles de energía discretos. Cuando se aplica a los orbitales atómicos, esto significa que las diferencias de energía entre estados también son discretas. Una transición entre estos estados (es decir, un electrón absorbiendo o emitiendo un fotón) sólo puede ocurrir si el fotón tiene una energía correspondiente a la diferencia de energía exacta entre dichos estados.

Considere dos estados del átomo de hidrógeno:

Estado n = 1, ℓ = 0, m _ℓ = 0 y m _s = +1/2
Estado n = 2, ℓ = 0, m _ℓ = 0 y m _s = −1/2

Según la teoría cuántica, el estado 1 tiene una energía fija de E ₁ y el estado 2 tiene una energía fija de E ₂. Ahora bien, ¿qué pasaría si un electrón en el estado 1 pasara al estado 2? Para que esto suceda, el electrón necesitaría ganar una energía de exactamente E ₂ − E ₁. Si el electrón recibe energía menor o mayor que este valor, no puede saltar del estado 1 al estado 2. Ahora, supongamos que irradiamos el átomo con una luz de amplio espectro. Fotones que llegan al átomo que tienen una energía de exactamente E ₂ − E ₁será absorbido por el electrón en el estado 1, y ese electrón saltará al estado 2. Sin embargo, los fotones que tienen mayor o menor energía no pueden ser absorbidos por el electrón, porque el electrón solo puede saltar a uno de los orbitales, no puede saltar a un estado entre orbitales. El resultado es que solo los fotones de una frecuencia específica serán absorbidos por el átomo. Esto crea una línea en el espectro, conocida como línea de absorción, que corresponde a la diferencia de energía entre los estados 1 y 2.

El modelo orbital atómico predice así espectros de líneas, que se observan experimentalmente. Esta es una de las principales validaciones del modelo orbital atómico.

No obstante, el modelo orbital atómico es una aproximación a la teoría cuántica completa, que solo reconoce muchos estados electrónicos. Las predicciones de los espectros de líneas son cualitativamente útiles pero no son cuantitativamente precisas para átomos e iones que no sean los que contienen un solo electrón.

Contenido relacionado

Más resultados...