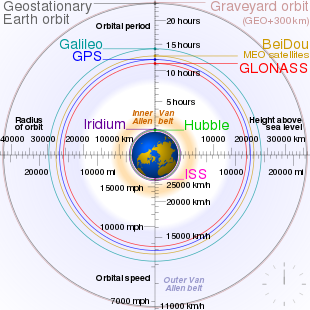
Órbita geoestacionaria

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Órbita circular sobre el Ecuador de la Tierra y siguiendo la dirección de la rotación de la Tierra

Dos satélites geoestacionarios en la misma órbita

Vista de 5° × 6° de una parte de la correa geoestacionaria, mostrando varios satélites geoestacionarios. Aquellos con inclinación 0° forman un cinturón diagonal a través de la imagen; algunos objetos con pequeñas inclinaciones al Ecuador son visibles por encima de esta línea. Los satélites son puntuales, mientras que las estrellas han creado senderos estelares debido a la rotación de la Tierra.

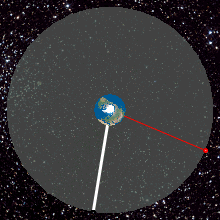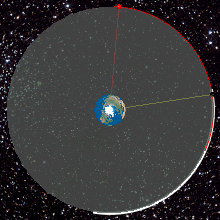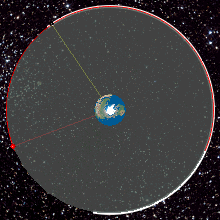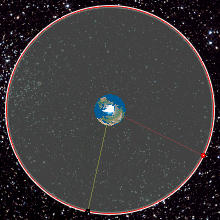
Una órbita geoestacionaria, también denominada órbita ecuatorial geosíncrona (GEO), es una órbita geosíncrona circular de 35 786 km (22,236 mi) en altitud sobre el ecuador de la Tierra (42 164 km (26 199 mi) de radio desde el centro de la Tierra) y siguiendo la dirección de rotación de la Tierra.

Un objeto en una órbita de este tipo tiene un período orbital igual al período de rotación de la Tierra, un día sideral, por lo que para los observadores terrestres parece inmóvil, en una posición fija en el cielo. El concepto de órbita geoestacionaria fue popularizado por el escritor de ciencia ficción Arthur C. Clarke en la década de 1940 como una forma de revolucionar las telecomunicaciones, y el primer satélite que se colocó en este tipo de órbita se lanzó en 1963.

Los satélites de comunicaciones a menudo se colocan en una órbita geoestacionaria para que las antenas satelitales terrestres no tengan que girar para rastrearlos, sino que puedan apuntar permanentemente a la posición en el cielo donde se encuentran los satélites. Los satélites meteorológicos también se colocan en esta órbita para el seguimiento y la recopilación de datos en tiempo real, y los satélites de navegación proporcionan un punto de calibración conocido y mejoran la precisión del GPS.

Los satélites geoestacionarios se lanzan a través de una órbita temporal y se colocan en una ranura sobre un punto particular en la superficie de la Tierra. La órbita requiere algo de mantenimiento de la posición para mantener su posición, y los satélites retirados modernos se colocan en una órbita de cementerio más alta para evitar colisiones.

Historia

Syncom 2, el primer satélite geosincrónico

En 1929, Herman Potočnik describió tanto las órbitas geosincrónicas en general como el caso especial de la órbita terrestre geoestacionaria en particular como órbitas útiles para las estaciones espaciales. La primera aparición de una órbita geoestacionaria en la literatura popular fue en octubre de 1942, en la primera historia de Venus Equilateral de George O. Smith, pero Smith no entró en detalles. El autor británico de ciencia ficción Arthur C. Clarke popularizó y amplió el concepto en un artículo de 1945 titulado Extra-Terrestrial Relays - Can Rocket Stations Give Worldwide Radio Coverage?, publicado en Wireless World revista. Clarke reconoció la conexión en su introducción a The Complete Venus Equilateral. La órbita, que Clarke describió por primera vez como útil para los satélites de comunicaciones de transmisión y retransmisión, a veces se denomina órbita de Clarke. De manera similar, la colección de satélites artificiales en esta órbita se conoce como Clarke Belt.

En la terminología técnica, la órbita se conoce como órbita ecuatorial geoestacionaria o geosíncrona, y los términos se usan indistintamente.

El primer satélite geoestacionario fue diseñado por Harold Rosen mientras trabajaba en Hughes Aircraft en 1959. Inspirado por el Sputnik 1, quería usar un satélite geoestacionario para globalizar las comunicaciones. Entonces, las telecomunicaciones entre EE. UU. y Europa eran posibles entre solo 136 personas a la vez y dependían de radios de alta frecuencia y un cable submarino.

La sabiduría convencional en ese momento era que se requeriría demasiada potencia de cohete para colocar un satélite en una órbita geoestacionaria y no sobreviviría lo suficiente como para justificar el gasto, por lo que los primeros esfuerzos se dirigieron hacia constelaciones de satélites en baja o media. órbita terrestre. El primero de ellos fueron los satélites de globo Echo pasivos en 1960, seguidos por Telstar 1 en 1962. Aunque estos proyectos tenían dificultades con la intensidad de la señal y el seguimiento, que podían resolverse a través de satélites geoestacionarios, el concepto se consideró poco práctico, por lo que Hughes a menudo retuvo. fondos y apoyo.

Para 1961, Rosen y su equipo habían producido un prototipo cilíndrico con un diámetro de 76 centímetros (30 pulgadas), una altura de 38 centímetros (15 pulgadas), un peso de 11,3 kilogramos (25 lb), ligero y lo suficientemente pequeño como para colocarlo en órbita. Fue estabilizado por giro con una antena dipolo que producía una forma de onda en forma de panqueque. En agosto de 1961, fueron contratados para comenzar a construir el satélite real. Perdieron Syncom 1 debido a una falla electrónica, pero Syncom 2 se colocó con éxito en una órbita geosincrónica en 1963. Aunque su órbita inclinada todavía requería antenas móviles, pudo retransmitir transmisiones de televisión y permitió que el presidente de los EE. UU., John F. Kennedy, llamara a Nigeria. primer ministro Abubakar Tafawa Balewa desde un barco el 23 de agosto de 1963.

El primer satélite colocado en una órbita geoestacionaria fue Syncom 3, que fue lanzado por un cohete Delta D en 1964. Con su mayor ancho de banda, este satélite pudo transmitir la cobertura en vivo de los Juegos Olímpicos de verano desde Japón a Estados Unidos. Las órbitas geoestacionarias han sido de uso común desde entonces, en particular para la televisión por satélite.

Hoy en día hay cientos de satélites geoestacionarios que brindan sensores remotos y comunicaciones.

Aunque la mayoría de las ubicaciones terrestres pobladas del planeta ahora tienen instalaciones de comunicaciones terrestres (microondas, fibra óptica), con acceso telefónico que cubre el 96 % de la población y acceso a Internet al 90 %, algunas áreas rurales y remotas en los países desarrollados aún dependen sobre comunicaciones por satélite.

Usos

La mayoría de los satélites de comunicaciones comerciales, satélites de transmisión y satélites SBAS operan en órbitas geoestacionarias.

Comunicaciones

Los satélites de comunicación geoestacionarios son útiles porque son visibles desde una gran área de la superficie terrestre, extendiéndose 81° tanto en latitud como en longitud. Aparecen estacionarios en el cielo, lo que elimina la necesidad de que las estaciones terrestres tengan antenas móviles. Esto significa que los observadores terrestres pueden erigir antenas pequeñas, baratas y estacionarias que siempre están dirigidas al satélite deseado. Sin embargo, la latencia se vuelve significativa, ya que una señal tarda unos 240 ms en pasar desde un transmisor terrestre en el ecuador hasta el satélite y viceversa. Este retraso presenta problemas para las aplicaciones sensibles a la latencia, como la comunicación de voz, por lo que los satélites de comunicación geoestacionarios se utilizan principalmente para entretenimiento unidireccional y aplicaciones donde no se encuentran disponibles alternativas de baja latencia.

Los satélites geoestacionarios están directamente sobre el ecuador y aparecen más bajos en el cielo para un observador más cercano a los polos. A medida que aumenta la latitud del observador, la comunicación se vuelve más difícil debido a factores como la refracción atmosférica, la emisión térmica de la Tierra, las obstrucciones en la línea de visión y los reflejos de la señal desde el suelo o las estructuras cercanas. En latitudes por encima de los 81°, los satélites geoestacionarios están por debajo del horizonte y no se pueden ver en absoluto. Debido a esto, algunos satélites de comunicación rusos han utilizado órbitas elípticas Molniya y Tundra, que tienen una excelente visibilidad en latitudes altas.

Meteorología

Se utiliza una red mundial de satélites meteorológicos geoestacionarios operativos para proporcionar imágenes visibles e infrarrojas de la superficie y la atmósfera de la Tierra para la observación meteorológica, la oceanografía y el seguimiento atmosférico. A partir de 2019, hay 19 satélites en funcionamiento o en espera. Estos sistemas satelitales incluyen:

la serie GOES de los Estados Unidos, operada por NOAA
the Meteosat series, launched by the European Space Agency and operated by the European Weather Satellite Organization, EUMETSAT
the Republic of Korea COMS-1 and GK-2A multi mission satellites.
los satélites rusos Elektro-L
la serie japonesa Himawari
Serie chino Fengyun
Serie INSAT de India

Estos satélites normalmente capturan imágenes en el espectro visual e infrarrojo con una resolución espacial de entre 0,5 y 4 kilómetros cuadrados. La cobertura suele ser de 70° y, en algunos casos, menos.

Las imágenes de satélites geoestacionarios se han utilizado para rastrear cenizas volcánicas, medir la temperatura de las nubes y el vapor de agua, oceanografía, medir la temperatura terrestre y la cobertura vegetal, facilitar la predicción de la trayectoria de los ciclones y proporcionar cobertura de nubes en tiempo real y otros datos de seguimiento. Parte de la información se ha incorporado a los modelos de predicción meteorológica, pero debido a su amplio campo de visión, monitoreo a tiempo completo y menor resolución, las imágenes de satélites meteorológicos geoestacionarios se utilizan principalmente para pronósticos a corto plazo y en tiempo real.

Navegación

Zonas de servicios de sistemas de aumento basados en satélites (SBAS).

Los satélites geoestacionarios se pueden utilizar para aumentar los sistemas GNSS mediante la transmisión de correcciones de errores ionosféricos, de efemérides y de reloj (calculados a partir de estaciones terrestres de una posición conocida) y proporcionando una señal de referencia adicional. Esto mejora la precisión de la posición de aproximadamente 5 ma 1 mo menos.

Los sistemas de navegación pasados y actuales que utilizan satélites geoestacionarios incluyen:

El Sistema de Ampliación de la Zona (WAAS), operado por la Administración Federal de Aviación de los Estados Unidos (FAA);
The European Geostationary Navigation Overlay Service (EGNOS), operated by the ESSP (en nombre del GSA de la UE);
The Multi-functional Satellite Augmentation System (MSAS), operated by Japan's Ministry of Land, Infrastructure and Transport Japan Civil Aviation Bureau (JCAB);
El sistema GPS Aided Geo Augmented Navigation (GAGAN) operado por la India.
Sistema de navegación comercial StarFire, operado por John Deere y C-Nav Positioning Solutions (Oceaneering);
El sistema comercial Starfix DGPS System y OmniSTAR, operado por Fugro.

Implementación

Lanzamiento

Ejemplo de una transición de la GTO temporal a la OSG.
Echo Estrella XVII· Tierra.

Los satélites geoestacionarios se lanzan hacia el este en una órbita progresiva que coincide con la tasa de rotación del ecuador. La inclinación más pequeña en la que se puede lanzar un satélite es la de la latitud del sitio de lanzamiento, por lo que lanzar el satélite desde cerca del ecuador limita la cantidad de cambio de inclinación necesario más adelante. Además, el lanzamiento desde cerca del ecuador permite que la velocidad de rotación de la Tierra impulse al satélite. Un sitio de lanzamiento debe tener agua o desiertos al este, para que los cohetes fallidos no caigan en un área poblada.

La mayoría de los vehículos de lanzamiento colocan los satélites geoestacionarios directamente en una órbita de transferencia geoestacionaria (GTO), una órbita elíptica con un apogeo a la altura de GEO y un perigeo bajo. Luego se utiliza la propulsión satelital a bordo para elevar el perigeo, circularizar y llegar a GEO.

Asignación de órbitas

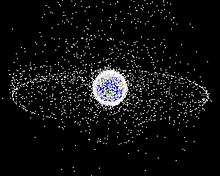
Todos los satélites en órbita geoestacionaria deben ocupar un solo anillo sobre el ecuador. El requisito de espaciar estos satélites para evitar interferencias de radiofrecuencia perjudiciales durante las operaciones significa que hay un número limitado de intervalos orbitales disponibles y, por lo tanto, solo un número limitado de satélites puede funcionar en órbita geoestacionaria. Esto ha llevado a un conflicto entre diferentes países que desean acceder a las mismas ranuras orbitales (países cercanos a la misma longitud pero con diferentes latitudes) y frecuencias de radio. Estas disputas se abordan a través del mecanismo de asignación de la Unión Internacional de Telecomunicaciones en virtud del Reglamento de Radiocomunicaciones. En la Declaración de Bogotá de 1976, ocho países ubicados en el ecuador de la Tierra reclamaron la soberanía sobre las órbitas geoestacionarias sobre su territorio, pero los reclamos no obtuvieron reconocimiento internacional.

Propuesta de estado

Una estatita es un satélite hipotético que utiliza la presión de radiación del sol contra una vela solar para modificar su órbita.

Mantendría su ubicación sobre el lado oscuro de la Tierra a una latitud de aproximadamente 30 grados. Una estatita es estacionaria en relación con el sistema de la Tierra y el Sol en lugar de compararla con la superficie de la Tierra, y podría aliviar la congestión en el anillo geoestacionario.

Satélites retirados

Los satélites geoestacionarios requieren cierto mantenimiento de la estación para mantener su posición y, una vez que se quedan sin combustible para los propulsores, por lo general se retiran. Los transpondedores y otros sistemas a bordo a menudo sobreviven al combustible del propulsor y, al permitir que el satélite se mueva naturalmente a una órbita geosincrónica inclinada, algunos satélites pueden permanecer en uso o bien elevarse a una órbita de cementerio. Este proceso se regula cada vez más y los satélites deben tener un 90 % de posibilidades de desplazarse más de 200 km por encima del cinturón geoestacionario al final de su vida útil.

Desechos espaciales

Earth from space, surrounded by small white dots

A computer-generated image from 2005 showing the distribution of mostly space debris in geocentric orbit with two areas of concentration: geostationary orbit and low Earth orbit.

Los desechos espaciales en órbitas geoestacionarias suelen tener una velocidad de colisión más baja que en la órbita terrestre baja (LEO), ya que todos los satélites GEO orbitan en el mismo plano, altitud y velocidad; sin embargo, la presencia de satélites en órbitas excéntricas permite colisiones de hasta 4 km/s. Aunque una colisión es comparativamente improbable, los satélites GEO tienen una capacidad limitada para evitar los escombros.

Los desechos de menos de 10 cm de diámetro no se pueden ver desde la Tierra, lo que dificulta evaluar su prevalencia.

A pesar de los esfuerzos por reducir el riesgo, se han producido colisiones de naves espaciales. El satélite de telecomunicaciones de la Agencia Espacial Europea Olympus-1 fue golpeado por un meteorito el 11 de agosto de 1993 y finalmente se movió a una órbita de cementerio, y en 2006 el satélite de comunicaciones Russian Express-AM11 fue golpeado por un objeto desconocido y quedó inoperable, aunque sus ingenieros tuvo suficiente tiempo de contacto con el satélite para enviarlo a una órbita de cementerio. En 2017, tanto AMC-9 como Telkom-1 se separaron por una causa desconocida.

Propiedades

Una órbita geoestacionaria típica tiene las siguientes propiedades:

Inclinación: 0°
Período: 1436 minutos (un día sidereal)
Eccentricidad: 0
Argumento de perigeo: indefinido
eje semi-major: 42,164 km

Inclinación

Una inclinación de cero asegura que la órbita permanezca sobre el ecuador en todo momento, haciéndola estacionaria con respecto a la latitud desde el punto de vista de un observador terrestre (y en el marco de referencia fijo en la Tierra centrado en la Tierra).

Período

El período orbital es igual a exactamente un día sideral. Esto significa que el satélite regresará al mismo punto sobre la superficie de la Tierra cada día (sideral), independientemente de otras propiedades orbitales. Para una órbita geoestacionaria en particular, asegura que mantenga la misma longitud a lo largo del tiempo. Este período orbital, T, está directamente relacionado con el semieje mayor de la órbita a través de la fórmula:

T=2pi {sqrt {a^{3} over mu }}

donde:

$a$ es la longitud del eje semi-major de la órbita
$μ$ es el parámetro gravitacional estándar del cuerpo central

Excentricidad

La excentricidad es cero, lo que produce una órbita circular. Esto garantiza que el satélite no se acerque ni se aleje de la Tierra, lo que provocaría que se desplazara hacia adelante y hacia atrás por el cielo.

Estabilidad orbital

Solo se puede lograr una órbita geoestacionaria a una altitud muy cercana a los 35 786 kilómetros (22 236 millas) y directamente sobre el ecuador. Esto equivale a una velocidad orbital de 3,07 kilómetros por segundo (1,91 millas por segundo) y un período orbital de 1.436 minutos, un día sidéreo. Esto asegura que el satélite coincidirá con el período de rotación de la Tierra y tendrá una huella estacionaria en el suelo. Todos los satélites geoestacionarios deben estar ubicados en este anillo.

Una combinación de la gravedad lunar, la gravedad solar y el aplanamiento de la Tierra en sus polos provoca un movimiento de precesión del plano orbital de cualquier objeto geoestacionario, con un período orbital de aproximadamente 53 años y un gradiente de inclinación inicial de aproximadamente 0,85 ° por año, logrando una inclinación máxima de 15° después de 26,5 años. Para corregir esta perturbación, son necesarias maniobras regulares de mantenimiento de la posición orbital, que ascienden a un delta-v de aproximadamente 50 m/s por año.

Un segundo efecto a tener en cuenta es la deriva longitudinal, provocada por la asimetría de la Tierra: el ecuador es ligeramente elíptico. Hay dos puntos de equilibrio estables (en 75,3°E y 108°O) y dos puntos inestables correspondientes (en 165,3°E y 14,7°O). Cualquier objeto geoestacionario colocado entre los puntos de equilibrio (sin ninguna acción) sería acelerado lentamente hacia la posición de equilibrio estable, provocando una variación periódica de longitud. La corrección de este efecto requiere maniobras de mantenimiento de la posición con un delta-v máximo de unos 2 m/s por año, dependiendo de la longitud deseada.

El viento solar y la presión de la radiación también ejercen pequeñas fuerzas sobre los satélites: con el tiempo, hacen que se alejen lentamente de sus órbitas prescritas.

En ausencia de misiones de servicio desde la Tierra o de un método de propulsión renovable, el consumo de propulsor para el mantenimiento de la estación limita la vida útil del satélite. Los propulsores de efecto Hall, actualmente en uso, tienen el potencial de prolongar la vida útil de un satélite al proporcionar una propulsión eléctrica de alta eficiencia.

Derivación de la altitud geoestacionaria

Comparación de la órbita geoestacionaria de la Tierra con órbitas del sistema de navegación por satélite GPS, GLONASS, Galileo y Compass (ordenada media terrestre) con la Estación Espacial Internacional, el Telescopio Espacial Hubble y las órbitas de constelación de Iridium y el tamaño nominal de la Tierra. La órbita de la Luna es alrededor de 9 veces mayor (en radio y longitud) que la órbita geoestacionaria.

Para órbitas circulares alrededor de un cuerpo, la fuerza centrípeta requerida para mantener la órbita (F_c) es igual a la fuerza gravitacional que actúa sobre el satélite ( F_g):

{displaystyle F_{text{c}}=F_{text{g}}}

De la ley de gravitación universal de Isaac Newton,

{displaystyle F_{text{g}}=G{frac {M_{text{E}}m_{text{s}}}{r^{2}}}}

donde F_g es la fuerza gravitatoria que actúa entre dos objetos, M_E es la masa del Tierra, 5.9736× 10²⁴ kg, m_s es la masa del satélite, r es la distancia entre los centros de sus masas, y G es la constante gravitacional, (6,67428±0.00067)×10⁻¹¹ m³ kg⁻¹ s⁻².

La magnitud de la aceleración, a, de un cuerpo que se mueve en un círculo está dada por:

{displaystyle a={frac {v^{2}}{r}}}

donde v es la magnitud de la velocidad (es decir, la rapidez) del satélite. De la segunda ley del movimiento de Newton, la fuerza centrípeta F_c viene dada por:

{displaystyle F_{text{c}}=m_{text{s}}{frac {v^{2}}{r}}}

Como F_c = F_g,

{displaystyle m_{text{s}}{frac {v^{2}}{r}}=G{frac {M_{text{E}}m_{text{s}}}{r^{2}}}}

para que

{displaystyle v^{2}=G{frac {M_{text{E}}}{r}}}

Reemplazar v con la ecuación de la velocidad de un objeto que se mueve alrededor de un círculo produce:

{displaystyle left({frac {2pi r}{T}}right)^{2}=G{frac {M_{text{E}}}{r}}}

donde T es el período orbital (es decir, un día sideral), y es igual a 86164.09054 s. Esto da una ecuación para r:

{displaystyle r={sqrt[{3}]{frac {GM_{text{E}}T^{2}}{4pi ^{2}}}}}

El producto GM_E se conoce con mucha mayor precisión que cualquier factor por separado; se conoce como la constante gravitacional geocéntrica μ = 398600.4418±0.0008 km³ s⁻². Por lo tanto

{displaystyle r={sqrt[{3}]{frac {mu T^{2}}{4pi ^{2}}}}}

El radio orbital resultante es de 42 164 kilómetros (26 199 millas). Restando el radio ecuatorial de la Tierra, 6.378 kilómetros (3.963 millas), da la altitud de 35.786 kilómetros (22.236 millas).

La velocidad orbital se calcula multiplicando la velocidad angular por el radio orbital:

{displaystyle v=omega rquad approx 3074.6~{text{m/s}}}

Marte

Con el mismo método, podemos determinar la altitud orbital de cualquier par de cuerpos similares, incluida la órbita areoestacionaria de un objeto en relación con Marte, si se supone que es esférico (que no lo es del todo). La constante gravitacional GM (μ) de Marte tiene el valor de 42830 km³ s⁻², su radio ecuatorial es 3389.50 km y el período de rotación conocido (T) del planeta es 1,02595676 días terrestres ( 88642.66 s). Usando estos valores, Mars' la altitud orbital es igual a 17039 km.

Notas explicativas

^ Órbita geoestacionaria y Órbita geosincrónica (ecuatorial) se utilizan de alguna manera intercambiable en las fuentes.
^ Los períodos y velocidades orbitales se calculan utilizando las relaciones 4π²R³=T²MM y V²R=MM, donde R es el radio de órbita en metros; T, el período orbital en segundos; V, la velocidad orbital en m/s; G, la constante gravitacional ♥ 6.673×10^{−11 -}Nm²/kg²; M, la masa de la Tierra ♥ 5.98×10²⁴kg.
^ La órbita de la Luna no es perfectamente circular, y está aproximadamente 8.6 veces más lejos de la Tierra que el anillo geoestacionario cuando la Luna está en perigeo (363 104 km ÷ 42 164 km) y 9.6 veces más lejos cuando la Luna está en apogeo (405,696 km ÷ 42,164 km).

Contenido relacionado

Más resultados...