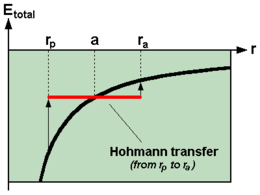
Órbita de transferencia de Hohmann

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Maniobra de transferencia de baja impulsión entre dos órbitas de diferentes alturas

órbita de transferencia Hohmann, etiquetada 2, de una órbita (1) a una órbita superior (3)

Un ejemplo de una órbita de transferencia Hohmann entre la Tierra y Marte, utilizado por la sonda InSight de la NASA.
InSight· Tierra· Marte

En astronáutica, la órbita de transferencia de Hohmann () es una maniobra orbital utilizada para transferir una nave espacial entre dos órbitas de diferentes altitudes alrededor de un cuerpo central. Se utilizarían ejemplos para viajes entre la órbita terrestre baja y la Luna, u otro planeta solar o asteroide. En el caso idealizado, las órbitas inicial y objetivo son tanto circulares como coplanares. La maniobra se logra colocando la nave en una órbita de transferencia elíptica que es tangencial a las órbitas inicial y objetivo. La maniobra utiliza dos encendidos impulsivos del motor: el primero establece la órbita de transferencia y el segundo ajusta la órbita para que coincida con el objetivo.

La maniobra de Hohmann a menudo utiliza la menor cantidad de impulso posible (que consume una cantidad proporcional de delta-v y, por lo tanto, de propulsor) para lograr la transferencia, pero requiere un tiempo de viaje relativamente más largo que las transferencias de mayor impulso. En algunos casos en los que una órbita es mucho más grande que la otra, una transferencia bielíptica puede usar incluso menos impulso, a costa de un tiempo de viaje aún mayor.

La maniobra lleva el nombre de Walter Hohmann, el científico alemán que publicó una descripción de ella en su libro de 1925 Die Erreichbarkeit der Himmelskörper (La accesibilidad de los cuerpos celestes). Hohmann fue influenciado en parte por el autor alemán de ciencia ficción Kurd Lasswitz y su libro de 1897 Dos planetas.

Cuando se utiliza para viajar entre cuerpos celestes, una órbita de transferencia de Hohmann requiere que los puntos de partida y de destino estén en ubicaciones particulares en sus órbitas entre sí. Las misiones espaciales que utilizan una transferencia Hohmann deben esperar a que se produzca esta alineación requerida, lo que abre una ventana de lanzamiento. Para una misión entre la Tierra y Marte, por ejemplo, estas ventanas de lanzamiento ocurren cada 26 meses. Una órbita de transferencia de Hohmann también determina un tiempo fijo requerido para viajar entre los puntos de partida y de destino; para un viaje Tierra-Marte este tiempo de viaje es de unos 9 meses. Cuando la transferencia se realiza entre órbitas cercanas a cuerpos celestes con una gravitación significativa, generalmente se requiere mucho menos delta-v, ya que el efecto Oberth puede emplearse para las quemaduras.

También se utilizan a menudo para estas situaciones, pero las transferencias de baja energía que tienen en cuenta las limitaciones de empuje de los motores reales y aprovechan los pozos de gravedad de ambos planetas pueden ser más eficientes en combustible.

Ejemplo

El diagrama muestra una órbita de transferencia de Hohmann para llevar una nave espacial desde una órbita circular inferior a una superior. Es una órbita elíptica que es tangencial tanto a la órbita circular inferior que dejará la nave espacial (cian, etiquetada como 1 en el diagrama) como a la órbita circular superior que alcanzará (roja, etiquetada como 3 en el diagrama). La órbita de transferencia (amarilla, etiquetada como 2 en el diagrama) se inicia al encender el motor de la nave espacial para agregar energía y aumentar el apogeo. Cuando la nave espacial alcanza su apogeo, el encendido de un segundo motor agrega energía para elevar el perigeo, poniendo a la nave espacial en la órbita circular más grande.

Debido a la reversibilidad de las órbitas, se puede usar una órbita de transferencia de Hohmann similar para llevar una nave espacial desde una órbita más alta a una más baja; en este caso, el motor de la nave espacial se enciende en la dirección opuesta a su trayectoria actual, lo que reduce la velocidad de la nave espacial y reduce su perigeo al de la órbita de transferencia elíptica. Luego, el motor se enciende nuevamente a la distancia más baja para reducir la velocidad de la nave espacial a la órbita circular inferior. La órbita de transferencia de Hohmann se basa en dos cambios instantáneos de velocidad. Se requiere combustible adicional para compensar el hecho de que las ráfagas toman tiempo; esto se minimiza mediante el uso de motores de alto empuje para minimizar la duración de las ráfagas. Para las transferencias en la órbita terrestre, las dos quemas se etiquetan como quemadura de perigeo y quema de apogeo (o patada de apogeo); de manera más general, se denominan quemaduras periapsis y apoapsis. Alternativamente, la segunda quema para circularizar la órbita puede denominarse quemadura de circularización.

Tipo I y Tipo II

Una órbita de transferencia de Hohmann ideal se transfiere entre dos órbitas circulares en el mismo plano y recorre exactamente 180° alrededor de la primaria. En el mundo real, la órbita de destino puede no ser circular y puede no ser coplanaria con la órbita inicial. Las órbitas de transferencia del mundo real pueden atravesar un poco más o un poco menos de 180° alrededor del primario. Una órbita que recorre menos de 180° alrededor de la primaria se denomina "Tipo I" Transferencia de Hohmann, mientras que una órbita que recorre más de 180° se denomina "Tipo II" Transferencia de Hohman.

Las órbitas de transferencia pueden dar más de 360° alrededor del sol. Estas transferencias de múltiples revoluciones a veces se denominan Tipo III y Tipo IV, donde un Tipo III es un Tipo I más 360° y un Tipo IV es un Tipo II más 360°.

Usos

Se puede usar una órbita de transferencia de Hohmann para transferir la órbita de un objeto hacia otro objeto, siempre que compartan un cuerpo común más masivo alrededor del cual orbitan. En el contexto de la Tierra y el Sistema Solar, esto incluye cualquier objeto que gire alrededor del Sol. Un ejemplo de dónde podría usarse una órbita de transferencia de Hohmann es poner un asteroide, que orbita alrededor del Sol, en contacto con la Tierra.

Cálculo

Para un pequeño cuerpo orbitando otro cuerpo mucho mayor, como un satélite orbitando la Tierra, la energía total del cuerpo más pequeño es la suma de su energía cinética y energía potencial, y esta energía total también equivale a la mitad del potencial en el distancia media $a$ (el eje semi-major):

{displaystyle E={frac {mv^{2}}{2}}-{frac {GMm}{r}}={frac {-GMm}{2a}}.}

Resolver esta ecuación para la velocidad da como resultado la ecuación vis-viva,

{displaystyle v^{2}=mu left({frac {2}{r}}-{frac {1}{a}}right),}

$v$ es la velocidad de un cuerpo en órbita,
$mu =GM$ es el parámetro gravitacional estándar del cuerpo primario, suponiendo ${displaystyle M+m}$ no es significativamente mayor que $M$ (que hace) ${displaystyle v_{M}ll v}$ ), (para la tierra, esto es μ~3.986E14 m³ s⁻²)
$r$ es la distancia del cuerpo orbitante del foco primario,
$a$ es el eje semi-major de la órbita del cuerpo.

Por lo tanto, el delta-v (Δv) requerido para la transferencia de Hohmann se puede calcular de la siguiente manera, bajo el supuesto de impulsos instantáneos:

{displaystyle Delta v_{1}={sqrt {frac {mu }{r_{1}}}}left({sqrt {frac {2r_{2}}{r_{1}+r_{2}}}}-1right),}

r=r_{1}

r_{1}

r_{2}

{displaystyle Delta v_{2}={sqrt {frac {mu }{r_{2}}}}left(1-{sqrt {frac {2r_{1}}{r_{1}+r_{2}}}}right),}

{displaystyle r=r_{2}}

r_{2}

r_{1}

r_{2}

r_{1}

r_{2}

mu

³²

r_{1}

r_{2}

Delta v

{displaystyle Delta v_{text{total}}=Delta v_{1}+Delta v_{2}.}

Ya sea que se mueva a una órbita más alta o más baja, según la tercera ley de Kepler, el tiempo necesario para transferir entre las órbitas es

{displaystyle t_{text{H}}={frac {1}{2}}{sqrt {frac {4pi ^{2}a_{text{H}}^{3}}{mu }}}=pi {sqrt {frac {(r_{1}+r_{2})^{3}}{8mu }}}}

{displaystyle a_{text{H}}}

En la aplicación para viajar de un cuerpo celeste a otro, es crucial comenzar la maniobra en el momento en que los dos cuerpos estén correctamente alineados. Teniendo en cuenta que la velocidad angular objetivo es

{displaystyle omega _{2}={sqrt {frac {mu }{r_{2}^{3}}}},}

{displaystyle alpha =pi -omega _{2}t_{text{H}}=pi left(1-{frac {1}{2{sqrt {2}}}}{sqrt {left({frac {r_{1}}{r_{2}}}+1right)^{3}}}right).}

Ejemplo

Balance total de energía durante una transferencia Hohmann entre dos órbitas circulares con primer radio

r_{p}

segundo radio

r_{a}

Considere una órbita de transferencia geoestacionaria, comenzando en r₁ = 6678 km (altitud 300 km) y terminando en una órbita geoestacionaria con r ₂ = 42 164 km (altitud 35 786 km).

En la órbita circular más pequeña, la velocidad es de 7,73 km/s; en el más grande, 3,07 km/s. En la órbita elíptica intermedia, la velocidad varía de 10,15 km/s en el perigeo a 1,61 km/s en el apogeo.

Por lo tanto, el Δv para la primera quema es 10,15 − 7,73 = 2,42 km/s, para la segunda quema 3,07 − 1,61 = 1,46 km/s, y para ambas juntas 3,88 km/s.

Esto es mayor que el Δv necesario para una órbita de escape: 10,93 − 7,73 = 3,20 km/s. Aplicar un Δv en la órbita terrestre baja (LEO) de solo 0,78 km/s más (3,20−2,42) le daría al cohete la velocidad de escape, que es menor que el Δv de 1,46 km/s necesario para circularizar la órbita geosincrónica. Esto ilustra el efecto Oberth de que, a grandes velocidades, el mismo Δv proporciona una energía orbital más específica, y el aumento de energía se maximiza si uno gasta el Δv lo más rápido posible, en lugar de gastar algo, siendo desacelerado por la gravedad, y luego gastando un poco más para superar la desaceleración (por supuesto, el objetivo de una órbita de transferencia de Hohmann es diferente).

Peor caso, máximo delta-v

Como muestra el ejemplo anterior, el Δv requerido para realizar una transferencia Hohmann entre dos órbitas circulares no es el mayor cuando el radio de destino es infinito. (La velocidad del paisaje es √2 tiempos de velocidad orbital, por lo que el Δv requerido para escapar es √2(41,4%) de la velocidad orbital.) El Δv requerido es mayor (53,0% de velocidad orbital más pequeña) cuando el radio de la órbita mayor es 15.5817... veces el de la órbita más pequeña. Este número es la raíz positiva $x 3 15 - 15 x 2 - 9 - x - 1 = 0$ , que es ${textstyle 5+4,{sqrt {7}}cos left({1 over 3}arctan {{sqrt {3}} over 37}right)}$ . Para mayores ratios de órbita $Δ v$ requerido para la segunda quemadura disminuye más rápido que los primeros aumentos.

Aplicación a viajes interplanetarios

Cuando se utiliza para mover una nave espacial de la órbita de un planeta a la órbita de otro, la situación se vuelve algo más compleja, pero se requiere mucho menos delta-v, debido al efecto Oberth, que la suma de el delta-v requerido para escapar del primer planeta más el delta-v requerido para una transferencia Hohmann al segundo planeta.

Por ejemplo, considere una nave espacial que viaja de la Tierra a Marte. Al comienzo de su viaje, la nave espacial ya tendrá una cierta velocidad y energía cinética asociada a su órbita alrededor de la Tierra. Durante la quema, el motor del cohete aplica su delta-v, pero la energía cinética aumenta como una ley cuadrática, hasta que es suficiente para escapar del potencial gravitacional del planeta, y luego se quema más hasta que para ganar suficiente energía para entrar en la órbita de transferencia de Hohmann (alrededor del Sol). Debido a que el motor del cohete es capaz de hacer uso de la energía cinética inicial del propulsor, se requiere mucho menos delta-v además de lo necesario para alcanzar la velocidad de escape, y la situación óptima es cuando la transferencia la quema se realiza a mínima altura (periapsis bajo) sobre el planeta. El delta-v necesario es de solo 3,6 km/s, solo alrededor de 0,4 km/s más de lo necesario para escapar de la Tierra, aunque esto da como resultado que la nave espacial vaya 2,9 km/s más rápido que la Tierra a medida que avanza. se dirige a Marte (ver tabla a continuación).

En el otro extremo, la nave espacial necesitará cierta velocidad para orbitar Marte, que en realidad será menor que la velocidad necesaria para seguir orbitando el Sol en la órbita de transferencia, y mucho menos para intentar orbitar el Sol en una órbita similar a la de Marte. orbita. Por lo tanto, la nave espacial tendrá que desacelerar para que la gravedad de Marte la capture. Esta quema de captura debe realizarse de manera óptima a baja altitud para aprovechar al máximo el efecto Oberth. Por lo tanto, se necesitan cantidades relativamente pequeñas de empuje en cada extremo del viaje para organizar la transferencia en comparación con la situación de espacio libre.

Sin embargo, con cualquier transferencia Hohmann, la alineación de los dos planetas en sus órbitas es crucial: el planeta de destino y la nave espacial deben llegar al mismo punto en sus respectivas órbitas alrededor del Sol al mismo tiempo. Este requisito de alineación da lugar al concepto de ventanas de lanzamiento.

El término órbita de transferencia lunar (LTO) se usa para la Luna.

Es posible aplicar la fórmula anterior para calcular el Δv en km/s necesario para entrar en una órbita de transferencia de Hohmann para llegar a varios destinos desde la Tierra (suponiendo órbitas circulares para los planetas). En esta tabla, la columna denominada "Δv para entrar en la órbita de Hohmann desde la órbita de la Tierra" da el cambio de la velocidad de la Tierra a la velocidad necesaria para llegar a una elipse de Hohmann cuyo otro extremo estará a la distancia deseada del Sol. La columna con la etiqueta "v saliendo de LEO" da la velocidad necesaria (en un marco de referencia no giratorio centrado en la tierra) cuando se encuentra a 300 km sobre la superficie terrestre. Esto se obtiene sumando a la energía cinética específica el cuadrado de la velocidad (7,73 km/s) de esta órbita terrestre baja (es decir, la profundidad del pozo de gravedad de la Tierra en este LEO). La columna "Δv de LEO" es simplemente la velocidad anterior menos 7,73 km/s.

Destino	Orbital radio (AU)	Δv (km/s)
Destino	Orbital radio (AU)	para entrar en la órbita de Hohmann de la órbita de la Tierra	salida LEO	desde LEO
Sol	0	29.8	31,7	24.0
Mercurio	0.39	7.5	13.3	5,5
Venus	0.72	2.5	11.2	3.5
Marte	1.52	2.9	11.3	3.6
Júpiter	5.2	8.8	14.0	6.3
Saturno	9.54	10.3	15.0	7.3
Urano	19.19	11.3	15.7	8.0
Neptuno	30.07	11.7	16.0	8.2
Plutón	39.48	11.8	16.1	8.4
Infinity	JUEGO	12.3	16,5	8.8

Tenga en cuenta que, en la mayoría de los casos, Δv desde LEO es menor que Δv para entrar en la órbita de Hohmann desde la órbita de la Tierra.

Para llegar al Sol, en realidad no es necesario usar un Δv de 24 km/s. Uno puede usar 8,8 km/s para alejarse mucho del Sol, luego usar un Δv insignificante para llevar el momento angular a cero y luego caer al Sol. Esto puede considerarse una secuencia de dos transferencias de Hohmann, una hacia arriba y otra hacia abajo. Además, la tabla no proporciona los valores que se aplicarían al usar la Luna como asistencia de gravedad. También hay posibilidades de usar un planeta, como Venus, que es el más fácil de alcanzar, para ayudar a llegar a otros planetas o al Sol.

Comparación con otras transferencias

Transferencia bielíptica

La transferencia biéptica consta de dos órbitas medias inteligentes. Desde la órbita inicial, una primera quema expulsa delta-v para impulsar la nave espacial en la primera órbita de transferencia con una apoapsis en algún punto $r_b$ lejos del cuerpo central. En este punto una segunda quemadura envía la nave espacial a la segunda órbita elíptica con periapsis en el radio de la órbita deseada final, donde se realiza una tercera quemadura, inyectando la nave espacial en la órbita deseada.

Si bien requieren una quema de motor más que una transferencia Hohmann y, por lo general, requieren un mayor tiempo de viaje, algunas transferencias bielípticas requieren una cantidad menor de delta-v total que una transferencia Hohmann cuando la relación de semi-mayor final a inicial eje es 11.94 o mayor, dependiendo del eje semi-mayor intermedio elegido.

La idea de la trayectoria de transferencia bielíptica fue publicada por primera vez por Ary Sternfeld en 1934.

Transferencia de bajo empuje

Los motores de bajo empuje pueden realizar una aproximación de una órbita de transferencia de Hohmann, al crear una ampliación gradual de la órbita circular inicial a través de encendidos del motor cuidadosamente sincronizados. Esto requiere un cambio en la velocidad (delta-v) que es mayor que la órbita de transferencia de dos impulsos y tarda más en completarse.

Los motores como los propulsores de iones son más difíciles de analizar con el modelo delta-v. Estos motores ofrecen un empuje muy bajo y, al mismo tiempo, un presupuesto delta-v mucho más alto, un impulso específico mucho más alto, una masa de combustible y motor más baja. Una maniobra de transferencia Hohmann de 2 encendidos no sería práctica con un empuje tan bajo; la maniobra optimiza principalmente el uso de combustible, pero en esta situación hay relativamente mucho.

Si solo se planean maniobras de bajo empuje en una misión, entonces encender continuamente un motor de bajo empuje pero de muy alta eficiencia podría generar un delta-v más alto y al mismo tiempo usar menos propulsor que un motor de cohete químico convencional.

Pasar de una órbita circular a otra cambiando gradualmente el radio simplemente requiere la misma delta-v que la diferencia entre las dos velocidades. Tal maniobra requiere más delta-v que una maniobra de transferencia de Hohmann de 2 quemadas, pero lo hace con un empuje bajo continuo en lugar de aplicaciones cortas de empuje alto.

La cantidad de masa propulsora utilizada mide la eficiencia de la maniobra más el hardware empleado para ello. El delta-v total utilizado mide únicamente la eficiencia de la maniobra. Para los sistemas de propulsión eléctrica, que tienden a ser de bajo empuje, la alta eficiencia del sistema de propulsión generalmente compensa el mayor delta-V en comparación con la maniobra de Hohmann más eficiente.

Las órbitas de transferencia que utilizan motores de propulsión eléctrica o de bajo empuje optimizan el tiempo de transferencia para alcanzar la órbita final y no la delta-v como en la órbita de transferencia de Hohmann. Para la órbita geoestacionaria, la órbita inicial se configura para que sea supersíncrona y empujando continuamente en la dirección de la velocidad en el apogeo, la órbita de transferencia se transforma en una geosíncrona circular. Sin embargo, este método lleva mucho más tiempo debido al bajo empuje inyectado en la órbita.

Red de Transporte Interplanetario

En 1997, se publicó un conjunto de órbitas conocido como Red de transporte interplanetario (ITN), que proporciona rutas delta-v de propulsión aún más bajas (aunque mucho más lentas y largas) entre diferentes órbitas que la transferencia de Hohmann. órbitas. La Red de Transporte Interplanetario es de naturaleza diferente a las transferencias de Hohmann porque las transferencias de Hohmann asumen solo un cuerpo grande mientras que la Red de Transporte Interplanetario no lo hace. La Red de Transporte Interplanetario es capaz de lograr el uso de delta-v menos propulsor empleando la asistencia de la gravedad de los planetas.

Fuentes generales

Walter Hohmann (1925). Die Erreichbarkeit der Himmelskörper. Verlag Oldenbourg en München. ISBN 3-486-23106-5.
Thornton, Stephen T.; Marion, Jerry B. (2003). Dinámica Clásica de partículas y sistemas (5th ed.). Brooks Cole. ISBN 0-534-40896-6.
Bate, R.R.; Mueller, D.D.; White, J.E. (1971). Fundamentos de Astrodinámica. Dover Publications, Nueva York. ISBN 978-0-486-60061-1.
Vallado, D. A. (2001). Fundamentos de Astrodinámica y Aplicaciones (2a edición). Springer. ISBN 978-0-7923-6903-5.
Battin, R.H. (1999). Introducción a las Matemáticas y Métodos de Astrodinámica. American Institute of Aeronautics " Ast, Washington, DC. ISBN 978-1-56347-342-5.

Contenido relacionado

Más resultados...