Onda transversal

Ilustración de una onda transversal simple (plano) propagando a través de un medio elástico en la dirección horizontal, con partículas desplazadas en la dirección vertical. Sólo se muestra una capa del material

Ilustración de los campos eléctricos (rojo) y magnéticos (azul) a lo largo de un rayo en una simple onda de luz. Para cualquier plano perpendicular al rayo, cada campo tiene siempre el mismo valor en todos los puntos del plano.

Propagación de una onda esférica transversal en una red 2d (modelo empírico)

En física, una onda transversal es una onda cuyas oscilaciones son perpendiculares a la dirección de avance de la onda. Esto contrasta con una onda longitudinal que viaja en la dirección de sus oscilaciones. Las ondas de agua son un ejemplo de onda transversal.

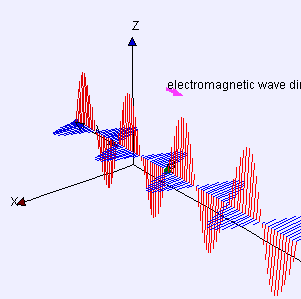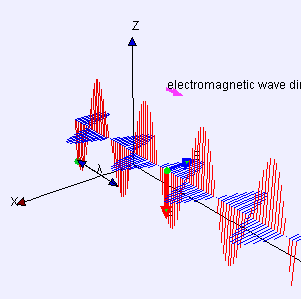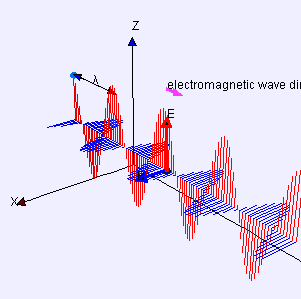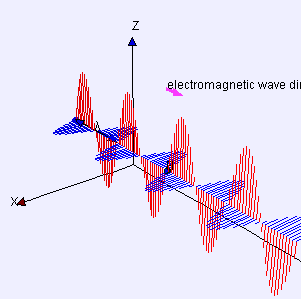
Un ejemplo simple es el de las ondas que se pueden crear en una longitud horizontal de cuerda anclando un extremo y moviendo el otro extremo hacia arriba y hacia abajo. Otro ejemplo son las ondas que se crean en la membrana de un tambor. Las ondas se propagan en direcciones paralelas al plano de la membrana, pero cada punto de la membrana se desplaza hacia arriba y hacia abajo, perpendicularmente a ese plano. La luz es otro ejemplo de onda transversal, donde las oscilaciones son los campos eléctrico y magnético, que apuntan en ángulo recto a los rayos de luz ideales que describen la dirección de propagación.

Las ondas transversales ocurren comúnmente en sólidos elásticos debido al esfuerzo cortante generado; las oscilaciones en este caso son el desplazamiento de las partículas sólidas fuera de su posición relajada, en direcciones perpendiculares a la propagación de la onda. Estos desplazamientos corresponden a una deformación por cortante local del material. Por lo tanto, una onda transversal de esta naturaleza se denomina onda de corte. Dado que los fluidos no pueden resistir las fuerzas de corte en reposo, la propagación de ondas transversales dentro de la mayor parte de los fluidos no es posible. En sismología, las ondas transversales también se denominan ondas secundarias u ondas S.

Las ondas transversales se contrastan con las ondas longitudinales, donde las oscilaciones ocurren en la dirección de la onda. El ejemplo estándar de una onda longitudinal es una onda de sonido u "onda de presión" en gases, líquidos o sólidos, cuyas oscilaciones provocan la compresión y expansión del material a través del cual se propaga la onda. Las ondas de presión se denominan "ondas primarias" u "ondas P" en geofísica.

Formulación matemática

Matemáticamente, el tipo más simple de onda transversal es una plana sinusoidal polarizada linealmente. "Avión" aquí significa que la dirección de propagación no cambia y es la misma en todo el medio; "linealmente polarizado" significa que la dirección del desplazamiento tampoco cambia y es la misma en todo el medio; y la magnitud del desplazamiento es una función sinusoidal sólo del tiempo y de la posición a lo largo de la dirección de propagación.

El movimiento de tal onda se puede expresar matemáticamente de la siguiente manera. Sea d la dirección de propagación (un vector con longitud unitaria), y o cualquier punto de referencia en el medio. Sea u la dirección de las oscilaciones (otro vector de longitud unitaria perpendicular a d). El desplazamiento de una partícula en cualquier punto p del medio y en cualquier tiempo t (segundos) será

S()p,t)=Aupecado⁡ ⁡ ()t− − ()p− − o)dvT+φ φ ){displaystyle S(p,t)=Ausin left({frac {t-(p-o){frac {d} {d}} {T}}+phi right)}

Según esta ecuación, la onda viaja en la dirección d y las oscilaciones ocurren de un lado a otro a lo largo de la dirección u. Se dice que la onda está polarizada linealmente en la dirección u.

Un observador que mira a un punto fijo p verá que la partícula allí se mueve en un movimiento armónico simple (sinusoidal) con un período T segundos, con un desplazamiento máximo de partículas A en cada sentido; es decir, con una frecuencia de f = 1/T ciclos completos de oscilación cada segundo. Una instantánea de todas las partículas en un tiempo fijo t mostrará el mismo desplazamiento para todas las partículas en cada plano perpendicular a d, con los desplazamientos en planos sucesivos formando un patrón sinusoidal, con cada ciclo completo extendiéndose a lo largo de d por la longitud de onda λ = v T = v/f. Todo el patrón se mueve en la dirección d con velocidad V.

La misma ecuación describe una onda de luz sinusoidal plana linealmente polarizada, excepto que el "desplazamiento" S(p, t) es el campo eléctrico en el punto p y el tiempo t. (El campo magnético se describirá con la misma ecuación, pero con una dirección de "desplazamiento" que es perpendicular tanto a d como a u, y una diferente amplitud.)

Principio de superposición

En un medio lineal homogéneo, las oscilaciones complejas (vibraciones en un material o flujos de luz) pueden describirse como la superposición de muchas ondas sinusoidales simples, ya sean transversales o longitudinales.

Las vibraciones de una cuerda de violín, por ejemplo, se pueden analizar como la suma de muchas ondas transversales de diferentes frecuencias, que desplazan la cuerda hacia arriba o hacia abajo o de izquierda a derecha. Las ondas en un estanque se pueden analizar como una combinación de ondas transversales y longitudinales (ondas de gravedad) que se propagan juntas.

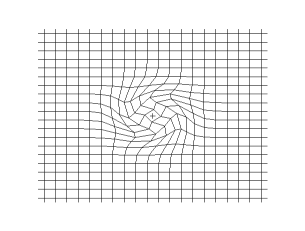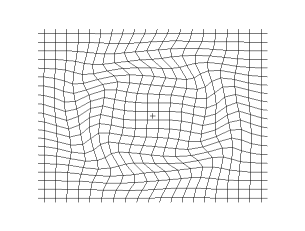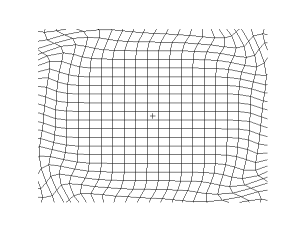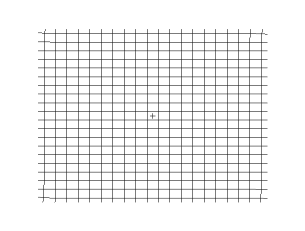
Polarización circular

Si el medio es lineal y permite múltiples direcciones de desplazamiento independientes para la misma dirección de viaje d, podemos elegir dos direcciones de polarización mutuamente perpendiculares y expresar cualquier onda polarizada linealmente en cualquier otra dirección como una combinación lineal (mezcla) de esas dos ondas.

Al combinar dos ondas con la misma frecuencia, velocidad y dirección de viaje, pero con diferentes fases y direcciones de desplazamiento independientes, se obtiene una onda polarizada circular o elípticamente. En tal onda, las partículas describen trayectorias circulares o elípticas, en lugar de moverse de un lado a otro.

Puede ayudar a la comprensión revisar el experimento mental con una cuerda tensa mencionado anteriormente. Tenga en cuenta que también puede lanzar ondas en la cuerda moviendo la mano hacia la derecha y hacia la izquierda en lugar de hacia arriba y hacia abajo. Éste es un punto importante. Hay dos direcciones independientes (ortogonales) en las que las ondas pueden moverse. (Esto es cierto para cualquier dos direcciones en ángulo recto, arriba y abajo y derecha e izquierda se eligen para mayor claridad). Cualquier onda lanzada al mover la mano en línea recta son ondas polarizadas linealmente.

Pero ahora imagina mover tu mano en un círculo. Tu movimiento lanzará una onda espiral en la cuerda. Estás moviendo tu mano simultáneamente hacia arriba y hacia abajo y de lado a lado. Los máximos del movimiento de lado a lado ocurren a un cuarto de longitud de onda (o un cuarto de vuelta alrededor del círculo, es decir, 90 grados o π/2 radianes) desde los máximos del movimiento hacia arriba y hacia abajo. En cualquier punto a lo largo de la cuerda, el desplazamiento de la cuerda describirá el mismo círculo que tu mano, pero retrasado por la velocidad de propagación de la onda. Tenga en cuenta también que puede elegir mover la mano en un círculo en el sentido de las agujas del reloj o en el sentido contrario a las agujas del reloj. Estos movimientos circulares alternos producen ondas polarizadas circularmente a derecha e izquierda.

En la medida en que su círculo sea imperfecto, un movimiento regular describirá una elipse y producirá ondas polarizadas elípticamente. En el extremo de la excentricidad, su elipse se convertirá en una línea recta, lo que producirá una polarización lineal a lo largo del eje principal de la elipse. Un movimiento elíptico siempre se puede descomponer en dos movimientos lineales ortogonales de amplitud desigual y desfasados 90 grados, siendo la polarización circular el caso especial en el que los dos movimientos lineales tienen la misma amplitud.

polarización circular generada mecánicamente en un hilo de goma, convertido a polarización lineal por un filtro polarizador mecánico.

Potencia en una onda transversal en cuerda

(Sea μ la densidad de masa lineal de la cuerda).

La energía cinética de un elemento de masa en una onda transversal viene dada por:

dK=12dmvSí.2=12μ μ dxA2⋅ ⋅ 2#2⁡ ⁡ ()2π π xλ λ − − ⋅ ⋅ t){displaystyle DK={frac {1}{2} dm ¿Qué? {1}{2}\fnK}m2}fnK}fnun}fnun}mfnuncio*

En una longitud de onda, la energía cinética

K=12μ μ A2⋅ ⋅ 2∫ ∫ 0λ λ #2⁡ ⁡ ()2π π xλ λ − − ⋅ ⋅ t)dx=14μ μ A2⋅ ⋅ 2λ λ {displaystyle K={frac {1}{2}mu} A^{2}omega ^{2}int ¿Por qué? }-omega tright)dx={frac {1}{4}mu} A^{2}omega ^{2}lambda }

Usando la ley de Hooke, la energía potencial en el elemento de masa

dU=12dm⋅ ⋅ 2Sí.2=12μ μ dx⋅ ⋅ 2A2pecado2⁡ ⁡ ()2π π xλ λ − − ⋅ ⋅ t){displaystyle dU={frac {2} {2}}momega ^{2} y^{2}={2}\mu dxomega A^{2}sin ^{2}left({frac {2pi x}{lambda }}-omega tright)}

Y la energía potencial para una longitud de onda

U=12μ μ A2⋅ ⋅ 2∫ ∫ 0λ λ pecado2⁡ ⁡ ()2π π xλ λ − − ⋅ ⋅ t)dx=14μ μ A2⋅ ⋅ 2λ λ {displaystyle U={frac {1}{2}mu} A^{2}omega ^{2}int ¿Por qué? }-omega tright)dx={frac {1}{4}mu} A^{2}omega ^{2}lambda }

Entonces, energía total en una longitud de onda K+U=12μ μ A2⋅ ⋅ 2λ λ {textstyle K+U={frac {1}{2}mu A^{2}omega ^{2}lambda }

Por lo tanto, el poder promedio es 12μ μ A2⋅ ⋅ 2vx{textstyle {frac {1}{2}mu} A^{2}omega ^{2}v_{x}