Omar Khayyam
Ghiyāth al-Dīn Abū al-Fatḥ ʿUmar ibn Ibrāhīm Nīsābūrī (18 de mayo de 1048 - 4 de diciembre de 1131), comúnmente conocido como Omar Khayyam (persa: عمر خیّام), fue un erudito, conocido por sus contribuciones a las matemáticas, la astronomía, la filosofía y la poesía persa. Nació en Nishapur, la capital inicial del Imperio Seljuk. Como erudito, fue contemporáneo del gobierno de la dinastía selyúcida en la época de la Primera Cruzada.
Como matemático, es más notable por su trabajo sobre la clasificación y solución de ecuaciones cúbicas, donde proporcionó soluciones geométricas por la intersección de cónicas. Khayyam también contribuyó a la comprensión del axioma paralelo. Como astrónomo, calculó la duración del año solar con notable precisión y exactitud, y diseñó el calendario Jalali, un calendario solar con un ciclo de intercalación muy preciso de 33 años que proporcionó la base para el calendario persa que todavía está en uso después casi un milenio.
Existe la tradición de atribuir poesía a Omar Khayyam, escrita en forma de cuartetas (rubāʿiyāt رباعیات). Esta poesía se hizo ampliamente conocida en el mundo de la lectura en inglés en una traducción de Edward FitzGerald (Rubaiyat of Omar Khayyam, 1859), que tuvo un gran éxito en el orientalismo de fin de siècle.
Vida
Omar Khayyam nació, de ascendencia persa Khorasani, en Nishapur en 1048. En los textos persas medievales se le suele llamar simplemente Omar Khayyam. Aunque abierto a dudas, a menudo se ha asumido que sus antepasados se dedicaron a la fabricación de tiendas de campaña, ya que Khayyam significa fabricante de tiendas en árabe. El historiador Bayhaqi, que conoció personalmente a Omar, proporciona los detalles completos de su horóscopo: "él era Géminis, el sol y Mercurio estaban en el ascendente[...]". Esto fue utilizado por los eruditos modernos para establecer su fecha de nacimiento como el 18 de mayo de 1048.
La infancia de Khayyam transcurrió en Nishapur, una importante metrópolis bajo el Gran Imperio Selyúcida, y había sido un importante centro de la religión zoroastriana. Su nombre completo, tal como aparece en las fuentes árabes, era Abu'l Fath Omar ibn Ibrahim al-Khayyam. Sus dones fueron reconocidos por sus primeros tutores, quienes lo enviaron a estudiar con el Imam Muwaffaq Nishaburi, el maestro más grande de la región de Khorasan, quien instruyó a los niños de la más alta nobleza. Omar hizo una gran amistad con él a través de los años. Khayyam también fue enseñado por el matemático zoroastriano Abu Hassan Bahmanyar bin Marzban. Tras estudiar ciencias, filosofía, matemáticas y astronomía en Nishapur, hacia el año 1068 viajó a la provincia de Bukhara, donde frecuentó la renombrada biblioteca del Arca. Hacia 1070 se trasladó a Samarcanda, donde comenzó a redactar su famoso tratado. sobre álgebra bajo el patrocinio de Abu Tahir Abd al-Rahman ibn ʿAlaq, el gobernador y juez superior de la ciudad. Omar Khayyam fue recibido amablemente por el gobernante Karakhanid Shams al-Mulk Nasr, quien según Bayhaqi, "le mostraría el mayor honor, tanto que lo sentaría [Omar] a su lado en su trono".
En 1073-1074 se firmó la paz con el sultán Malik-Shah I, que había realizado incursiones en los dominios de Karakhanid. Khayyam entró al servicio de Malik-Shah en 1074-5 cuando fue invitado por el Gran Visir Nizam al-Mulk a encontrarse con Malik-Shah en la ciudad de Marv. Posteriormente, Khayyam recibió el encargo de establecer un observatorio en Isfahan y dirigir a un grupo de científicos en la realización de observaciones astronómicas precisas destinadas a la revisión del calendario persa. La empresa comenzó probablemente en 1076 y terminó en 1079 cuando Omar Khayyam y sus colegas concluyeron sus mediciones de la duración del año, reportándolo como 365.24219858156 días. Dado que la duración del año cambia en el sexto lugar decimal durante la vida de una persona, esto es extraordinariamente preciso. A modo de comparación, la duración del año a finales del siglo XIX era de 365,242196 días, mientras que hoy es de 365,242190 días.
Después de la muerte de Malik-Shah y su visir (asesinados, se cree, por la orden de Asesinos ismaelitas), Omar perdió el favor de la corte y, como resultado, pronto emprendió su peregrinaje a La Meca. Un posible motivo oculto de su peregrinaje informado por Al-Qifti fue una demostración pública de su fe con el fin de disipar las sospechas de escepticismo y refutar las acusaciones de heterodoxia (incluida la posible simpatía o adhesión al zoroastrismo) que le hizo un clero hostil.. Luego fue invitado por el nuevo sultán Sanjar a Marv, posiblemente para trabajar como astrólogo de la corte. Más tarde se le permitió regresar a Nishapur debido al deterioro de su salud. A su regreso, parece haber vivido la vida de un recluso.
Omar Khayyam murió a la edad de 83 años en su ciudad natal de Nishapur el 4 de diciembre de 1131 y está enterrado en lo que ahora es el mausoleo de Omar Khayyam. Uno de sus discípulos, Nizami Aruzi, relata la historia de que en algún momento entre 1112 y 113, Khayyam estaba en Balkh en compañía de Al-Isfizari (uno de los científicos que había colaborado con él en el calendario de Jalali) cuando hizo una profecía de que "mi sepulcro estará en un lugar donde el viento del norte pueda esparcir rosas sobre él". Cuatro años después de su muerte, Aruzi localizó su tumba en un cementerio en un barrio entonces grande y conocido de Nishapur en el camino a Marv. Como había sido previsto por Khayyam, Aruzi encontró la tumba situada al pie de un muro del jardín sobre el cual los perales y los melocotoneros habían asomado sus cabezas y dejado caer sus flores de modo que su lápida quedó oculta debajo de ellos.
Matemáticas
Khayyam fue famoso durante su vida como matemático. Sus obras matemáticas sobrevivientes incluyen: Un comentario sobre las dificultades relacionadas con los postulados de los Elementos de Euclides (Risāla fī šarḥ mā aškala min muṣādarāt kitāb Uqlīdis, completado en diciembre de 1077), Sobre la división de un cuadrante de un círculo ( Risālah fī qismah rub' al-dā'irah, sin fecha pero completado antes del tratado sobre álgebra), y Sobre pruebas de problemas relacionados con el álgebra i> (Maqāla fi l-jabr wa l-muqābala, probablemente completado en 1079). Además, escribió un tratado sobre el teorema del binomio y la extracción de la raíz enésima de los números naturales, que se ha perdido.
Teoría de los paralelos
Una parte del comentario de Khayyam sobre los Elementos de Euclides trata sobre el axioma paralelo. El tratado de Khayyam puede considerarse el primer tratamiento del axioma no basado en petitio principii, sino en un postulado más intuitivo. Khayyam refuta los intentos previos de otros matemáticos de probar la proposición, principalmente sobre la base de que cada uno de ellos había postulado algo que no era de ninguna manera más fácil de admitir que el propio Quinto Postulado. Basándose en los puntos de vista de Aristóteles, rechaza el uso del movimiento en geometría y, por lo tanto, descarta el intento diferente de Al-Haytham. Insatisfecho con el fracaso de los matemáticos para probar la afirmación de Euclides a partir de sus otros postulados, Omar trató de conectar el axioma con el Cuarto Postulado, que establece que todos los ángulos rectos son iguales entre sí.
Khayyam fue el primero en considerar los tres casos distintos de ángulo agudo, obtuso y recto para los ángulos superiores de un cuadrilátero de Khayyam-Saccheri. Después de probar una serie de teoremas sobre ellos, demostró que el Postulado V se deriva de la hipótesis del ángulo recto y refutó los casos obtuso y agudo como contradictorios. Su elaborado intento de demostrar el postulado de las paralelas fue significativo para el desarrollo posterior de la geometría, ya que muestra claramente la posibilidad de geometrías no euclidianas. Ahora se sabe que las hipótesis de los ángulos agudo, obtuso y recto conducen respectivamente a la geometría hiperbólica no euclidiana de Gauss-Bolyai-Lobachevsky, a la geometría de Riemann y a la geometría euclidiana.
Los comentarios de Tusi sobre el tratamiento de los paralelos por parte de Khayyam llegaron a Europa. John Wallis, profesor de geometría en Oxford, tradujo el comentario de Tusi al latín. El geómetra jesuita Girolamo Saccheri, cuyo trabajo (euclides ab omni naevo vindicatus, 1733) generalmente se considera el primer paso en el eventual desarrollo de la geometría no euclidiana, estaba familiarizado con el trabajo de Wallis. El historiador estadounidense de las matemáticas David Eugene Smith menciona que Saccheri "utilizaba el mismo lema que el de Tusi, incluso rotulando la figura exactamente de la misma manera y utilizando el lema con el mismo propósito". Dice además que "Tusi establece claramente que se debe a Omar Khayyam, y del texto, parece claro que este último fue su inspirador".
El concepto de número real
Este tratado sobre Euclides contiene otra contribución que trata sobre la teoría de las proporciones y la composición de razones. Khayyam analiza la relación entre el concepto de proporción y el concepto de número y plantea explícitamente varias dificultades teóricas. En particular, contribuye al estudio teórico del concepto de número irracional. Disgustado con la definición de Euclides de proporciones iguales, redefinió el concepto de número mediante el uso de una fracción continua como medio para expresar una proporción. Rosenfeld y Youschkevitch (1973) argumentan que "al colocar cantidades y números irracionales en la misma escala operativa, [Khayyam] inició una verdadera revolución en la doctrina del número". Asimismo, D. J. Struik señaló que Omar estaba "en el camino hacia esa extensión del concepto de número que conduce a la noción de número real".
Álgebra geométrica
Rashed y Vahabzadeh (2000) han argumentado que debido a su enfoque geométrico completo de las ecuaciones algebraicas, Khayyam puede considerarse el precursor de Descartes en la invención de la geometría analítica. En El Tratado sobre la división de un cuadrante de un círculo Khayyam aplicó el álgebra a la geometría. En este trabajo se dedicó principalmente a investigar si es posible dividir un cuadrante circular en dos partes de manera que los segmentos de recta proyectados desde el punto de división a los diámetros perpendiculares del círculo formen una determinada proporción. Su solución, a su vez, empleó varias construcciones de curvas que condujeron a ecuaciones que contenían términos cúbicos y cuadráticos.
La solución de ecuaciones cúbicas
Khayyam parece haber sido el primero en concebir una teoría general de las ecuaciones cúbicas y el primero en resolver geométricamente todo tipo de ecuaciones cúbicas, en lo que respecta a las raíces positivas. El tratado de álgebra contiene su trabajo sobre ecuaciones cúbicas. Se divide en tres partes: (i) ecuaciones que pueden resolverse con compás y regla, (ii) ecuaciones que pueden resolverse mediante secciones cónicas y (iii) ecuaciones que involucran el inverso de la incógnita.
Khayyam produjo una lista exhaustiva de todas las ecuaciones posibles que involucran líneas, cuadrados y cubos. Consideró tres ecuaciones binomiales, nueve ecuaciones trinominales y siete ecuaciones tetranomiales. Para los polinomios de primer y segundo grado, proporcionó soluciones numéricas por construcción geométrica. Llegó a la conclusión de que hay catorce tipos diferentes de cúbicas que no se pueden reducir a una ecuación de menor grado. Para estos no pudo realizar la construcción de su segmento desconocido con compás y regla. Procedió a presentar soluciones geométricas a todo tipo de ecuaciones cúbicas utilizando las propiedades de las secciones cónicas. Los lemas de requisitos previos para la prueba geométrica de Khayyam incluyen Euclides VI, Proposición 13 y Apolonio II, Proposición 12. La raíz positiva de una ecuación cúbica se determinó como la abscisa de un punto de intersección de dos cónicas, por ejemplo, la intersección de dos parábolas, o la intersección de una parábola y un círculo, etc. Sin embargo, reconoció que el problema aritmético de estas cúbicas aún estaba sin resolver, y agregó que "posiblemente alguien más llegue a saberlo después de nosotros". Esta tarea permaneció abierta hasta el siglo XVI, cuando Cardano, Del Ferro y Tartaglia en la Italia del Renacimiento encontraron la solución algebraica de la ecuación cúbica en su generalidad.
Quien piensa que el álgebra es un truco para obtener desconocidos lo ha pensado en vano. No debe prestarse atención al hecho de que el álgebra y la geometría son diferentes en apariencia. Los álgebras son hechos geométricos que son probados por las proposiciones cinco y seis del Libro dos de Elementos.
Omar Khayyam
En efecto, el trabajo de Khayyam es un esfuerzo por unificar el álgebra y la geometría. Esta solución geométrica particular de ecuaciones cúbicas ha sido investigada más a fondo por M. Hachtroudi y extendida a la resolución de ecuaciones de cuarto grado. Aunque métodos similares habían aparecido esporádicamente desde Menaechmus, y desarrollados aún más por el matemático del siglo X Abu al-Jud, el trabajo de Khayyam puede considerarse el primer estudio sistemático y el primer método exacto para resolver ecuaciones cúbicas. El matemático Woepcke (1851), que ofreció traducciones del álgebra de Khayyam al francés, lo elogió por su "poder de generalización y su procedimiento rigurosamente sistemático".
Teorema del binomio y extracción de raíces
De los indios uno tiene métodos para obtener raíces cuadradas y cubo, métodos basados en el conocimiento de casos individuales – es decir, el conocimiento de los cuadrados de los nueve dígitos 12, 22, 32 (etc.) y sus respectivos productos, es decir, 2 × 3 etc. Hemos escrito un tratado sobre la prueba de la validez de esos métodos y que satisfacen las condiciones. Además, hemos aumentado sus tipos, es decir, en forma de determinación de la cuarta, quinta, sexta raíces hasta cualquier grado deseado. Nadie nos precedió en esto y esas pruebas son puramente aritméticas, fundadas en la aritmética de Los Elementos.
Omar Khayyam, Tratar sobre la demostración de problemas de álgebra
En su tratado algebraico, Khayyam alude a un libro que había escrito sobre la extracción de la n{displaystyle n}a raíz de los números usando una ley que había descubierto que no dependía de figuras geométricas. Este libro fue probablemente titulado Las dificultades de la aritmética ()Moškelāt al-hesāb), y no es extante. Basado en el contexto, algunos historiadores de matemáticas como D. J. Struik, creen que Omar debe haber conocido la fórmula para la expansión del binomio ()a+b)n{displaystyle (a+b)} {n}, donde n es un entero positivo. El caso del poder 2 se declara explícitamente en los elementos de Euclides y el caso de la mayoría de poder 3 había sido establecido por los matemáticos indios. Khayyam fue el matemático que notó la importancia de un teorema binomial general. El argumento que apoya la afirmación de que Khayyam tenía un teorema binomial general se basa en su capacidad de extraer raíces. Uno de los predecesores de Khayyam, Al-Karaji, ya había descubierto la disposición triangular de los coeficientes de expansiones binomiales que los europeos llegaron a conocer más tarde como triángulo de Pascal; Khayyam popularizó esta matriz triangular en Irán, de modo que ahora se conoce como triángulo de Omar Khayyam.
Astronomía
En 1074–5, el sultán Malik-Shah encargó a Omar Khayyam que construyera un observatorio en Isfahan y reformara el calendario persa. Había un panel de ocho eruditos trabajando bajo la dirección de Khayyam para realizar observaciones astronómicas a gran escala y revisar las tablas astronómicas. Recalibrar el calendario fijó el primer día del año en el momento exacto del paso del centro del Sol a través del equinoccio vernal. Esto marca el comienzo de la primavera o Nowrūz, un día en el que el Sol entra en el primer grado de Aries antes del mediodía. El calendario resultante recibió el nombre de calendario Jalālī en honor a Malik-Shah y se inauguró el 15 de marzo de 1079. El observatorio en sí quedó en desuso después de la muerte de Malik-Shah en 1092.
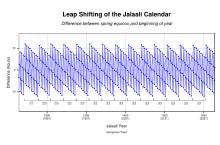
El calendario Jalālī era un verdadero calendario solar donde la duración de cada mes es igual al tiempo del paso del Sol por el signo del Zodíaco correspondiente. La reforma del calendario introdujo un ciclo de intercalación único de 33 años. Como indican los trabajos de Khazini, el grupo de Khayyam implementó un sistema de intercalación basado en años bisiestos cuatrienales y quinquenales. Por lo tanto, el calendario constaba de 25 años ordinarios que incluían 365 días y 8 años bisiestos que incluían 366 días. El calendario permaneció en uso en todo el Gran Irán desde el siglo XI hasta el siglo XX. En 1911, el calendario Jalali se convirtió en el calendario nacional oficial de Qajar Irán. En 1925 se simplificó este calendario y se modernizaron los nombres de los meses, dando como resultado el calendario iraní moderno. El calendario Jalali es más preciso que el calendario gregoriano de 1582, con un error de un día acumulando más de 5000 años, en comparación con un día cada 3330 años en el calendario gregoriano. Moritz Cantor lo consideró el calendario más perfecto jamás ideado.
Uno de sus alumnos Nizami Aruzi de Samarcanda relata que Khayyam aparentemente no creía en la astrología y la adivinación: "No observé que él (scil. Omar Khayyam) tuviera alguna gran creencia en las predicciones astrológicas, ni he visto ni oído hablar de ninguno de los grandes [científicos] que tenían tal creencia." Mientras trabajaba para Sultan Sanjar como astrólogo, se le pidió que predijera el clima, un trabajo que aparentemente no hizo bien. George Saliba (2002) explica que el término 'ilm al-nujūm, utilizado en varias fuentes en las que Se pueden encontrar referencias a la vida y obra de Omar, a veces se ha traducido incorrectamente para significar astrología. Agrega: "al menos desde mediados del siglo X, según la enumeración de las ciencias de Farabi, que esta ciencia, 'ilm al-nujūm, ya estaba dividido en dos partes, una que trata sobre astrología y la otra sobre astronomía matemática teórica."
Otras obras
Tiene un breve tratado dedicado a Arquímedes' principio (en título completo, Sobre el engaño de conocer las dos cantidades de oro y plata en un compuesto hecho de los dos). Para un compuesto de oro adulterado con plata, describe un método para medir más exactamente el peso por capacidad de cada elemento. Implica pesar el compuesto tanto en el aire como en el agua, ya que los pesos son más fáciles de medir exactamente que los volúmenes. Repitiendo lo mismo con el oro y la plata, uno encuentra exactamente cuánto más pesados que el agua eran el oro, la plata y el compuesto. Este tratado fue examinado extensamente por Eilhard Wiedemann, quien creía que la solución de Khayyam era más precisa y sofisticada que la de Khazini y Al-Nayrizi, quienes también trataron el tema en otros lugares.
Otro tratado breve se ocupa de la teoría de la música en el que analiza la conexión entre la música y la aritmética. La contribución de Khayyam fue proporcionar una clasificación sistemática de escalas musicales y discutir la relación matemática entre notas, menor, mayor y tetracordios.
Poesía
La primera alusión a la poesía de Omar Khayyam es del historiador Imad ad-Din al-Isfahani, un contemporáneo más joven de Khayyam, quien lo identifica explícitamente como poeta y científico (Kharidat al-qasr, 1174). Uno de los primeros especímenes del Rubiyat de Omar Khayyam es de Fakhr al-Din Razi. En su obra Al-tanbih 'ala ba'd asrar al-maw'dat fi'l-Qur'an (ca. 1160), cita uno de sus poemas (correspondiente a la cuarteta LXII de la primera edición de FitzGerald). Daya en sus escritos (Mirsad al-'Ibad, ca. 1230) cita dos cuartetas, una de las cuales es el mismo que el ya informado por Razi. El historiador Juvayni cita una cuarteta adicional (Tarikh-i Jahangushay, ca. 1226–1283). En 1340, Jajarmi incluye trece cuartetas de Khayyam en su obra que contiene una antología de las obras de poetas persas famosos (Munis al-ahrār), dos de los cuales han sido conocidos hasta ahora por las fuentes más antiguas. Un manuscrito relativamente tardío es el Bodleian MS. Ouseley 140, escrito en Shiraz en 1460, que contiene 158 cuartetos en 47 folios. El manuscrito perteneció a William Ouseley (1767–1842) y fue comprado por la Biblioteca Bodleian en 1844.
Hay citas ocasionales de versos atribuidos a Omar en textos atribuidos a autores de los siglos XIII y XIV, pero son de dudosa autenticidad, por lo que los estudiosos escépticos señalan que toda la tradición puede ser pseudoepigráfica.
Hans Heinrich Schaeder en 1934 comentó que el nombre de Omar Khayyam "debe ser tachado de la historia de la literatura persa" debido a la falta de cualquier material que se le pueda atribuir con confianza. De Blois (2004) presenta una bibliografía de la tradición manuscrita y concluye con pesimismo que la situación no ha cambiado significativamente desde la época de Schaeder. Cinco de las cuartetas atribuidas posteriormente a Omar se encuentran 30 años después de su muerte, citadas en Sindbad-Nameh. Si bien esto establece que estos versos específicos estaban en circulación en la época de Omar o poco después, no implica que los versos deban ser suyos. De Blois concluye que, al menos, el proceso de atribución de poesía a Omar Khayyam parece haber comenzado ya en el siglo XIII. Edward Granville Browne (1906) señala la dificultad de separar las cuartetas auténticas de las espurias: “si bien es cierto que Khayyam escribió muchas cuartetas, es casi imposible, salvo en unos pocos casos excepcionales, afirmar positivamente que escribió alguna de ellas. los que se le atribuyen".
Además de las cuartetas persas, hay veinticinco poemas árabes atribuidos a Khayyam que están atestiguados por historiadores como al-Isfahani, Shahrazuri (Nuzhat al-Arwah, ca. 1201–1211), Qifti (Tārikh al-hukamā, 1255) y Hamdallah Mustawfi (Tarikh-i guzida, 1339).
Boyle y Frye (1975) enfatizan que hay varios otros eruditos persas que ocasionalmente escribieron cuartetas, incluidos Avicena, Ghazzali y Tusi. Concluyen que también es posible que para Khayyam la poesía fuera una diversión en sus horas de ocio: "estos breves poemas parecen haber sido a menudo obra de eruditos y científicos que los compusieron, quizás, en momentos de relajación para edificar o divertir al círculo íntimo de sus discípulos".
La poesía atribuida a Omar Khayyam ha contribuido en gran medida a su fama popular en el período moderno como resultado directo de la extrema popularidad de la traducción de dichos versos al inglés por parte de Edward FitzGerald (1859). El Rubaiyat de Omar Khayyam de FitzGerald contiene traducciones sueltas de cuartetas del manuscrito de Bodleian. Tuvo tal éxito en el período de fin de siècle que una bibliografía compilada en 1929 enumeró más de 300 ediciones separadas, y desde entonces se han publicado muchas más.
Filosofía
Khayyam se consideraba intelectualmente un estudiante de Avicena. Según Al-Bayhaqi, estaba leyendo la metafísica del Libro de la Curación de Avicena antes de morir. Hay seis artículos filosóficos que se cree que fueron escritos por Khayyam. Uno de ellos, Sobre la existencia (Fi'l-wujūd), fue escrito originalmente en persa y trata el tema de la existencia y su relación con los universales. Otro artículo, titulado La necesidad de la contradicción en el mundo, el determinismo y la subsistencia (Darurat al-tadād fi'l- 'ālam wa'l-jabr wa'l-baqā'), está escrito en árabe y trata sobre el libre albedrío y el determinismo. Los títulos de sus otras obras son Sobre el ser y la necesidad (Risālah fī'l-kawn wa'l-taklīf), El Tratado sobre la trascendencia en la existencia (Al-Risālah al-ulā fi' l-wujūd), Sobre el conocimiento de los principios universales de la existencia (Risālah dar 'ilm kulliyāt-i wujūd), y Resumen sobre fenómenos naturales (Mukhtasar fi'l-Tabi'iyyāt).
Puntos de vista religiosos
Una lectura literal de las cuartetas de Khayyam conduce a la interpretación de su actitud filosófica hacia la vida como una combinación de pesimismo, nihilismo, epicureísmo, fatalismo y agnosticismo. Este punto de vista es adoptado por iranólogos como Arthur Christensen, H. Schaeder, Richard N. Frye, E. D. Ross, E. H. Whinfield y George Sarton. Por el contrario, las cuartetas de Khayyamic también se han descrito como poesía mística sufí. Además de sus cuartetas persas, J. C. E. Bowen (1973) menciona que los poemas árabes de Khayyam también "expresan un punto de vista pesimista que está totalmente en consonancia con la perspectiva del filósofo racionalista profundamente reflexivo que se sabe históricamente que Khayyam tiene sido." Edward FitzGerald enfatizó el escepticismo religioso que encontró en Khayyam. En su prefacio al Rubáiyát afirmó que "era odiado y temido por los sufíes", y negó cualquier pretensión de alegoría divina: "su vino es el verdadero jugo de la Uva: su Taberna, donde se tomaba: su Saki, la Carne y la Sangre que se la derramaban." Sadegh Hedayat es uno de los defensores más notables de la filosofía de Khayyam como escepticismo agnóstico y, según Jan Rypka (1934), llegó a considerar a Khayyam un ateo. Hedayat (1923) afirma que "mientras Khayyam cree en la transmutación y transformación del cuerpo humano, no cree en un alma separada; si tenemos suerte, nuestras partículas corporales se utilizarán para hacer una jarra de vino." La poesía de Omar Khayyam ha sido citada en el contexto del nuevo ateísmo, como en The Portable Atheist de Christopher Hitchens.
Al-Qifti (ca. 1172-1248) parece confirmar esta visión de la filosofía de Omar. En su obra The History of Learned Men, informa que los poemas de Omar solo tenían un estilo sufí exteriormente, pero estaban escritos con una agenda antirreligiosa. También menciona que en un momento fue acusado de impiedad, pero realizó una peregrinación para demostrar que era piadoso. Cuenta el relato que al regresar a su ciudad natal ocultó sus más profundas convicciones y practicó una vida estrictamente religiosa, acudiendo mañana y tarde al lugar de culto.
En el contexto de un artículo titulado Sobre el conocimiento de los principios de la existencia, Khayyam respalda el camino sufí. Csillik (1960) sugiere la posibilidad de que Omar Khayyam pudiera ver en el sufismo un aliado contra la religiosidad ortodoxa. Otros comentaristas no aceptan que la poesía de Omar tenga una agenda antirreligiosa e interpretan sus referencias al vino y la embriaguez en el sentido metafórico convencional común en el sufismo. El traductor francés J. B. Nicolas sostuvo que las constantes exhortaciones de Omar a beber vino no deben tomarse literalmente, sino que deben considerarse a la luz del pensamiento sufí donde la embriaguez embriagadora por el 'vino' debe entenderse como una metáfora del estado de iluminación o éxtasis divino de baqaa. La visión de Omar Khayyam como sufí fue defendida por Bjerregaard (1915), Idries Shah (1999) y Dougan (1991), quien atribuye la reputación de hedonismo a las fallas de la traducción de FitzGerald, argumentando que Omar' Su poesía debe entenderse como "profundamente esotérica". Por otro lado, expertos iraníes como Mohammad Ali Foroughi y Mojtaba Minovi rechazaron la hipótesis de que Omar Khayyam fuera sufí. Foroughi afirmó que las ideas de Khayyam pueden haber sido consistentes con las de los sufíes en ocasiones, pero no hay evidencia de que fuera formalmente un sufí. Aminrazavi (2007) afirma que "la interpretación sufí de Khayyam solo es posible mediante la lectura extensa de su Rubāʿīyyāt y ampliando el contenido para que se ajuste a la doctrina sufí clásica." Además, Frye (1975) enfatiza que Khayyam era muy detestado por varios célebres místicos sufíes que pertenecían al mismo siglo. Esto incluye a Shams Tabrizi (guía espiritual de Rumi), Najm al-Din Daya, quien describió a Omar Khayyam como "un filósofo infeliz, ateo y materialista", y Attar, quien lo consideró no como un compañero místico sino como un científico librepensador que esperaba castigos en el más allá.
Seyyed Hossein Nasr argumenta que es "reduccionista" usar una interpretación literal de sus versos (muchos de los cuales son de autenticidad incierta para empezar) para establecer la filosofía de Omar Khayyam. En cambio, aduce la traducción interpretativa de Khayyam del tratado Discurso sobre la unidad de Avicena ( Al-Khutbat al-Tawhīd), donde expresa puntos de vista ortodoxos sobre la Unidad Divina de acuerdo con el autor. Las obras en prosa que se cree que son de Omar están escritas en estilo peripatético y son explícitamente teístas, y tratan temas como la existencia de Dios y la teodicea. Como señaló Bowen, estas obras indican su participación en los problemas de la metafísica más que en las sutilezas del sufismo. Como evidencia de la fe de Khayyam y/o conformidad con las costumbres islámicas, Aminrazavi menciona que en sus tratados ofrece saludos y oraciones, alabando a Dios y Mahoma. En la mayoría de los extractos biográficos, se lo menciona con honoríficos religiosos como Imām, El Patrón of Faith (Ghīyāth al-Dīn), y La evidencia de la verdad (Hujjat al-Haqq). También señala que los biógrafos que alaban su religiosidad generalmente evitan hacer referencia a su poesía, mientras que los que mencionan su poesía a menudo no alaban su carácter religioso. Por ejemplo, el relato de Al-Bayhaqi, que antecede en algunos años a otros avisos biográficos, habla de Omar como un hombre muy piadoso que profesó puntos de vista ortodoxos hasta el último momento.
Sobre la base de toda la evidencia textual y biográfica existente, la pregunta permanece un tanto abierta y, como resultado, Khayyam ha recibido apreciaciones y críticas marcadamente contradictorias.
Recepción
Los diversos extractos biográficos que se refieren a Omar Khayyam lo describen como alguien sin igual en conocimientos y logros científicos durante su época. Muchos lo llamaban por el epíteto Rey de los Sabios (árabe: ملك الحکماء). Shahrazuri (m. 1300) lo estima mucho como matemático y afirma que puede ser considerado como "el sucesor de Avicena en las diversas ramas del saber filosófico". Al-Qifti (m. 1248), aunque no está de acuerdo con sus puntos de vista, admite que "no tenía rival en su conocimiento de la filosofía natural y la astronomía". A pesar de ser aclamado como poeta por una serie de biógrafos, según Richard N. Frye "todavía es posible argumentar que el estatus de Khayyam como poeta de primer rango es un desarrollo relativamente tardío". 34;
Thomas Hyde fue el primer europeo en llamar la atención sobre Omar y en traducir una de sus cuartetas al latín (Historia religionis veterum Persarum eorumque magorum, 1700). El interés occidental en Persia creció con el movimiento del orientalismo en el siglo XIX. Joseph von Hammer-Purgstall (1774–1856) tradujo algunos de los poemas de Khayyam al alemán en 1818 y Gore Ouseley (1770–1844) al inglés en 1846, pero Khayyam permaneció relativamente desconocido en Occidente hasta después de la publicación de Edward FitzGerald's Rubaiyat of Omar Khayyam en 1859. El trabajo de FitzGerald al principio no tuvo éxito, pero fue popularizado por Whitley Stokes a partir de 1861 y el trabajo llegó a ser muy admirado por el Prerrafaelitas. En 1872, FitzGerald hizo imprimir una tercera edición que aumentó el interés por la obra en Estados Unidos. En la década de 1880, el libro era extremadamente conocido en todo el mundo de habla inglesa, hasta el punto de la formación de numerosos "Omar Khayyam Clubs" y un "fin de siècle culto de los Rubaiyat". Los poemas de Khayyam se han traducido a muchos idiomas; muchos de los más recientes son más literales que el de FitzGerald.
La traducción de FitzGerald fue un factor que reavivó el interés por Khayyam como poeta, incluso en su Irán natal. Sadegh Hedayat en sus Songs of Khayyam (Taranehha-ye Khayyam, 1934) reintrodujo el legado poético de Omar en el Irán moderno. Bajo la dinastía Pahlavi, se erigió sobre su tumba un nuevo monumento de mármol blanco, diseñado por el arquitecto Houshang Seyhoun. En la década de 1960 se erigió una estatua de Abolhassan Sadighi en Laleh Park, Teherán, y se colocó un busto del mismo escultor cerca del mausoleo de Khayyam en Nishapur. En 2009, el estado de Irán donó un pabellón a la Oficina de las Naciones Unidas en Viena, inaugurado en el Centro Internacional de Viena. En 2016, se inauguraron tres estatuas de Khayyam: una en la Universidad de Oklahoma, una en Nishapur y otra en Florencia, Italia. Más de 150 compositores han utilizado el Rubaiyat como fuente de inspiración. El primer compositor de este tipo fue Liza Lehmann.
FitzGerald tradujo el nombre de Omar como "Tentmaker", y el nombre en inglés de "Omar the Tentmaker" resonó en la cultura popular de habla inglesa durante un tiempo. Así, Nathan Haskell Dole publicó una novela llamada Omar, the Tentmaker: A Romance of Old Persia en 1898. Omar the Tentmaker of Naishapur es una novela histórica de John Smith Clarke, publicado en 1910. "Omar the Tentmaker" es también el título de una obra de teatro de 1914 de Richard Walton Tully en un escenario oriental, adaptada como película muda en 1922. El general estadounidense Omar Bradley recibió el apodo de "Omar the Tent-Maker" en la Segunda Guerra Mundial.
La cuarteta del dedo que se mueve
La cuarteta de Omar Khayyam conocida como "The Moving Finger", en la forma de su traducción del poeta inglés Edward Fitzgerald, es una de las cuartetas más populares de la anglosfera. Se lee:
El Finger Moving escribe; y habiendo escrito,
Continúa: ni toda tu piedad ni tu sabiduría
Lo llevaremos a cancelar la mitad de la Línea,
Ni todas tus lágrimas lavan una Palabra de ella.
El título de la novela "El dedo que se mueve" escrito por Agatha Christie y publicado en 1942 se inspiró en esta cuarteta de la traducción de Rubaiyat de Omar Khayyam de Edward Fitzgerald. Martin Luther King también cita esta cuarteta de Omar Khayyam en uno de sus discursos 'Más allá de Vietnam: A Time to Break Silence':
Podemos clamar desesperadamente por tiempo para pausar en su pasaje, pero el tiempo es firme en cada petición y se apresura. Sobre los huesos blanqueados y los residuos jumbled de numerosas civilizaciones se escriben las palabras patéticas, "Demasiado tarde". Hay un libro invisible de la vida que registra fielmente nuestra vigilancia o nuestro abandono. Omar Khayyam tiene razón: “El dedo en movimiento escribe, y el hecho de escribir se mueve”.
En uno de sus discursos de disculpa por el escándalo Clinton-Lewinsky, Bill Clinton, el presidente número 42 de los EE. UU., también cita esta cuarteta.
Otras referencias de la cultura popular
El escritor franco-libanés Amin Maalouf basó la primera mitad de su novela de ficción histórica Samarcanda en la vida de Khayyam y la creación de su Rubaiyat. El escultor Eduardo Chillida produjo cuatro piezas de hierro macizo tituladas Mesa de Omar Khayyam (Mesa de Omar Khayyam) en la década de 1980.
El cráter lunar Omar Khayyam recibió su nombre en su honor en 1970, al igual que el planeta menor 3095 Omarkhayyam descubierto por la astrónoma soviética Lyudmila Zhuravlyova en 1980.
Google ha lanzado dos Google Doodles en su memoria. El primero fue en su cumpleaños número 964 el 18 de mayo de 2012. El segundo fue en su cumpleaños número 971 el 18 de mayo de 2019.
Galería
Contenido relacionado
Oda
Chicos Beagle
Mitopoeia