Ola

Olas superficiales en agua mostrando las ondas de agua

En física, matemáticas y campos relacionados, una onda es una perturbación dinámica que se propaga (cambio del equilibrio) de una o más cantidades. Las ondas pueden ser periódicas, en cuyo caso esas cantidades oscilan repetidamente alrededor de un valor de equilibrio (reposo) a alguna frecuencia. Cuando toda la forma de onda se mueve en una dirección, se dice que es una onda viajera; por el contrario, un par de ondas periódicas superpuestas que viajan en direcciones opuestas forman una onda estacionaria. En una onda estacionaria, la amplitud de la vibración tiene valores nulos en algunas posiciones donde la amplitud de la onda parece menor o incluso cero. Las ondas a menudo se describen mediante una ecuación de onda (campo de ondas estacionarias de dos ondas opuestas) o una ecuación de onda unidireccional para la propagación de una sola onda en una dirección definida.

Dos tipos de ondas se estudian más comúnmente en la física clásica. En una onda mecánica, los campos de tensión y deformación oscilan en torno a un equilibrio mecánico. Una onda mecánica es una deformación local (tensión) en algún medio físico que se propaga de partícula a partícula creando tensiones locales que también causan tensión en las partículas vecinas. Por ejemplo, las ondas de sonido son variaciones de la presión local y el movimiento de las partículas que se propagan a través del medio. Otros ejemplos de ondas mecánicas son las ondas sísmicas, las ondas de gravedad, las ondas superficiales, las vibraciones de cuerdas y los vórtices. En una onda electromagnética (como la luz), el acoplamiento entre los campos eléctrico y magnético sostiene la propagación de una onda que involucra estos campos de acuerdo con las ecuaciones de Maxwell. Las ondas electromagnéticas pueden viajar a través del vacío ya través de algunos medios dieléctricos (en longitudes de onda en las que se consideran transparentes). Las ondas electromagnéticas, de acuerdo con sus frecuencias (o longitudes de onda) tienen designaciones más específicas que incluyen ondas de radio, radiación infrarroja, ondas de terahercios, luz visible, radiación ultravioleta, rayos X y rayos gamma.

Otros tipos de ondas incluyen ondas gravitacionales, que son perturbaciones en el espacio-tiempo que se propagan según la relatividad general; ondas de difusión de calor; ondas de plasma que combinan deformaciones mecánicas y campos electromagnéticos; ondas de reacción-difusión, como en la reacción de Belousov-Zhabotinsky; y muchos más. Las ondas mecánicas y electromagnéticas transfieren energía, cantidad de movimiento e información, pero no transfieren partículas en el medio. En matemáticas y electrónica las ondas se estudian como señales. Por otro lado, algunas ondas tienen envolventes que no se mueven en absoluto como las ondas estacionarias (que son fundamentales para la música) y los saltos hidráulicos. Algunas, como las ondas de probabilidad de la mecánica cuántica, pueden ser completamente estáticas.

Ejemplo de ondas biológicas que se expanden sobre la corteza cerebral, ejemplo de despolarizaciones generalizadas.

Un campo de ondas físicas casi siempre está confinado a una región finita del espacio, llamada su dominio. Por ejemplo, las ondas sísmicas generadas por los terremotos son significativas sólo en el interior y superficie del planeta, por lo que pueden ser ignoradas fuera de él. Sin embargo, las ondas con dominio infinito, que se extienden por todo el espacio, se estudian comúnmente en matemáticas y son herramientas muy valiosas para comprender las ondas físicas en dominios finitos.

Una onda plana es una idealización matemática importante donde la perturbación es idéntica a lo largo de cualquier plano (infinito) normal a una dirección de viaje específica. Matemáticamente, la onda más simple es una onda plana sinusoidal en la que en cualquier punto el campo experimenta un movimiento armónico simple en una frecuencia. En medios lineales, las ondas complicadas generalmente se pueden descomponer como la suma de muchas ondas planas sinusoidales que tienen diferentes direcciones de propagación y/o diferentes frecuencias. Una onda plana se clasifica como onda transversal si la perturbación del campo en cada punto se describe mediante un vector perpendicular a la dirección de propagación (también la dirección de transferencia de energía); o onda longitudinal si esos vectores están alineados con la dirección de propagación. Las ondas mecánicas incluyen ondas transversales y longitudinales; por otro lado, las ondas planas electromagnéticas son estrictamente transversales, mientras que las ondas sonoras en fluidos (como el aire) solo pueden ser longitudinales. Esa dirección física de un campo oscilante en relación con la dirección de propagación también se denomina polarización de la onda, que puede ser un atributo importante.

Descripción matemática

Ondas simples

Una onda se puede describir como un campo, es decir, como una función F()x,t){displaystyle F(x,t)} Donde x{displaystyle x} es una posición y t{displaystyle t} es un momento.

El valor de x{displaystyle x} es un punto de espacio, específicamente en la región donde se define la ola. En términos matemáticos, es generalmente un vector en el espacio tridimensional cartesiano R3{displaystyle mathbb {R} {} {}}}. Sin embargo, en muchos casos uno puede ignorar una dimensión, y dejar x{displaystyle x} ser un punto del plano cartesiano R2{displaystyle mathbb {R} {2}}. Este es el caso, por ejemplo, al estudiar vibraciones de una piel de tambor. Incluso se puede restringir x{displaystyle x} a un punto de la línea cartesiana R{displaystyle mathbb {R} - es decir, el conjunto de números reales. Este es el caso, por ejemplo, cuando se estudian vibraciones en una cadena o grabador de violín. El tiempo t{displaystyle t}, por otro lado, siempre se supone que es un escalar; es decir, un número real.

El valor de F()x,t){displaystyle F(x,t)} puede ser cualquier cantidad física de interés asignado al punto x{displaystyle x} que puede variar con el tiempo. Por ejemplo, si F{displaystyle F} representa las vibraciones dentro de un sólido elástico, el valor de F()x,t){displaystyle F(x,t)} es generalmente un vector que da el desplazamiento actual de x{displaystyle x} de las partículas materiales que estarían en el punto x{displaystyle x} en ausencia de vibración. Para una onda electromagnética, el valor de F{displaystyle F} puede ser el vector de campo eléctrico E{displaystyle E}, o el vector de campo magnético H{displaystyle H., o cualquier cantidad relacionada, como el vector Poynting E× × H{displaystyle Etimes H}. En la dinámica del fluido, el valor F()x,t){displaystyle F(x,t)} podría ser el vector de velocidad del fluido en el punto x{displaystyle x}, o cualquier propiedad de escalar como presión, temperatura o densidad. En una reacción química, F()x,t){displaystyle F(x,t)} podría ser la concentración de alguna sustancia en el barrio del punto x{displaystyle x} del medio de reacción.

Para cualquier dimensión d{displaystyle d} (1, 2, o 3), el dominio de la onda es entonces un subconjunto D{displaystyle D} de Rd{displaystyle mathbb {R}, tal que el valor de la función F()x,t){displaystyle F(x,t)} se define para cualquier punto x{displaystyle x} dentro D{displaystyle D}. Por ejemplo, al describir el movimiento de una piel de tambor, se puede considerar D{displaystyle D} para ser un disco (círculo) en el plano R2{displaystyle mathbb {R} {2}} con centro en el origen ()0,0){displaystyle (0,0)}, y dejar F()x,t){displaystyle F(x,t)} ser el desplazamiento vertical de la piel en el punto x{displaystyle x} de D{displaystyle D} y a la vez t{displaystyle t}.

Familias de olas

A veces uno está interesado en una sola ola específica. Sin embargo, más a menudo, uno necesita comprender un gran conjunto de posibles ondas; como todas las formas en que la piel de un tambor puede vibrar después de ser golpeada una vez con una baqueta, o todos los posibles ecos de radar que uno podría obtener de un avión que se aproxima a un aeropuerto.

En algunas de esas situaciones, se puede describir tal familia de olas por función F()A,B,...... ;x,t){displaystyle F(A,B,ldots;x,t)} que depende de ciertos parámetros A,B,...... {displaystyle A,B,ldots, además x{displaystyle x} y t{displaystyle t}. Entonces uno puede obtener diferentes ondas —es decir, diferentes funciones de x{displaystyle x} y t{displaystyle t} — eligiendo diferentes valores para esos parámetros.

Presión de sonido onda de pie en un tubo medio abierto jugando la séptima armónica del fundamental (n 4)

Por ejemplo, la presión del sonido dentro de una grabadora que reproduce un sonido "puro" nota es típicamente una onda estacionaria, que se puede escribir como

F()A,L,n,c;x,t)=A()#⁡ ⁡ 2π π x2n− − 14L)()#⁡ ⁡ 2π π ct2n− − 14L){displaystyle F(A,L,n,c;x,t)=Aleft(cos 2pi x{frac {2n-1}{4L}right)left(cos 2pi ct{frac {2n-1}{4L}right)}

El parámetro A{displaystyle A} define la amplitud de la onda (es decir, la presión máxima del sonido en el agujero, que está relacionada con la intensidad de la nota); c{displaystyle c} es la velocidad del sonido; L{displaystyle L. es la longitud del agujero; y n{displaystyle n} es un entero positivo (1,2,3,...) que especifica el número de nodos en la onda de pie. (La posición x{displaystyle x} debe ser medido desde la boquilla, y el tiempo t{displaystyle t} desde cualquier momento en que la presión en la boquilla es máxima. La cantidad λ λ =4L/()2n− − 1){displaystyle lambda =4L/(2n-1)} es la longitud de onda de la nota emitida, y f=c/λ λ {displaystyle f=c/lambda} es su frecuencia.) Muchas propiedades generales de estas ondas se pueden inferir de esta ecuación general, sin elegir valores específicos para los parámetros.

Como otro ejemplo, puede ser que las vibraciones de una piel de tambor después de una sola huelga dependan sólo de la distancia r{displaystyle r} desde el centro de la piel hasta el punto de huelga, y en la fuerza s{displaystyle s} de la huelga. Entonces la vibración para todas las huelgas posibles puede ser descrita por una función F()r,s;x,t){displaystyle F(r,s;x,t)}.

A veces la familia de olas de interés tiene infinitamente muchos parámetros. Por ejemplo, uno puede querer describir lo que sucede con la temperatura en una barra de metal cuando se calienta inicialmente a varias temperaturas a diferentes puntos a lo largo de su longitud, y luego se permite enfriar por sí mismo en vacío. En ese caso, en lugar de un escalar o vector, el parámetro tendría que ser una función h{displaystyle h} tales que h()x){displaystyle h(x)} es la temperatura inicial en cada punto x{displaystyle x} del bar. Entonces las temperaturas en tiempos posteriores pueden ser expresadas por una función F{displaystyle F} que depende de la función h{displaystyle h} (es decir, un operador funcional), por lo que la temperatura en un momento posterior es F()h;x,t){displaystyle F(h;x,t)}

Ecuaciones de onda diferencial

Otra manera de describir y estudiar una familia de ondas es dar una ecuación matemática que, en lugar de dar explícitamente el valor de F()x,t){displaystyle F(x,t)}, sólo limita cómo esos valores pueden cambiar con el tiempo. Entonces la familia de olas en cuestión consiste en todas las funciones F{displaystyle F} que satisfacen esas limitaciones, es decir, todas las soluciones de la ecuación.

Este enfoque es extremadamente importante en la física, ya que las limitaciones suelen ser consecuencia de los procesos físicos que causan que la onda evolucione. Por ejemplo, si F()x,t){displaystyle F(x,t)} es la temperatura dentro de un bloque de algún material sólido homogéneo e isotrópico, su evolución se ve limitada por la ecuación diferencial parcial

∂ ∂ F∂ ∂ t()x,t)=α α ()∂ ∂ 2F∂ ∂ x12()x,t)+∂ ∂ 2F∂ ∂ x22()x,t)+∂ ∂ 2F∂ ∂ x32()x,t))+β β Q()x,t){displaystyle {frac {partial F}{partial t}(x,t)=alpha left({frac {partial ^{2}F}{partial x_{1}} {x,t)+{frac {partial ^{2}F}{partial x_{2}} {x,t)+{frac {partial ^{2}F}{partial x_{3} {2} {x,t)right)+beta Q(x,t)}

Donde Q()p,f){displaystyle Q(p,f)} es el calor que se genera por unidad de volumen y tiempo en el barrio x{displaystyle x} a la vez t{displaystyle t} (por ejemplo, por reacciones químicas que ocurren allí); x1,x2,x3{displaystyle x_{1},x_{2},x_{3} son las coordenadas cartesianas del punto x{displaystyle x}; ∂ ∂ F/∂ ∂ t{displaystyle partial F/partial t} es el (primero) derivado de F{displaystyle F} con respecto a t{displaystyle t}; y ∂ ∂ 2F/∂ ∂ xi2{displaystyle partial ^{2}F/partial # es el segundo derivado de F{displaystyle F} relativa a xi{displaystyle x_{i}}. (El símbolo "∂ ∂ {displaystyle partial }" está destinado a significar que, en el derivado con respecto a alguna variable, todas las demás variables deben ser consideradas fijas.)

Esta ecuación se puede derivar de las leyes de la física que gobiernan la difusión del calor en medios sólidos. Por esa razón, se llama la ecuación del calor en matemáticas, aunque se aplica a muchas otras cantidades físicas además de las temperaturas.

Por otro ejemplo, podemos describir todos los sonidos posibles haciendo eco dentro de un contenedor de gas por una función F()x,t){displaystyle F(x,t)} que da la presión en un punto x{displaystyle x} y tiempo t{displaystyle t} dentro de ese contenedor. Si el gas estaba inicialmente a temperatura y composición uniforme, la evolución de F{displaystyle F} se ve limitada por la fórmula

∂ ∂ 2F∂ ∂ t2()x,t)=α α ()∂ ∂ 2F∂ ∂ x12()x,t)+∂ ∂ 2F∂ ∂ x22()x,t)+∂ ∂ 2F∂ ∂ x32()x,t))+β β P()x,t){displaystyle {frac {partial ^{2}F}{partial t^{2}}(x,t)=alpha left({frac {partial t^{2}}}=alpha left ^{2}F}{partial x_{1}} {x,t)+{frac {partial ^{2}F}{partial x_{2}} {x,t)+{frac {partial ^{2}F}{partial x_{3} {2} {x,t)right)+beta P(x,t)}

Aquí. P()x,t){displaystyle P(x,t)} es una fuerza de compresión adicional que se está aplicando al gas cerca x{displaystyle x} por algún proceso externo, como un altavoz o un pistón al lado p{displaystyle p}.

Esta misma ecuación diferencial describe el comportamiento de las vibraciones mecánicas y los campos electromagnéticos en un sólido isotrópico homogéneo no conductor. Tenga en cuenta que esta ecuación difiere de la del flujo de calor sólo en que el lado izquierdo es ∂ ∂ 2F/∂ ∂ t2{displaystyle partial ^{2}F/partial t^{2}, el segundo derivado de F{displaystyle F} con respecto al tiempo, en lugar del primer derivado ∂ ∂ F/∂ ∂ t{displaystyle partial F/partial t}. Sin embargo, este pequeño cambio hace una gran diferencia en el conjunto de soluciones F{displaystyle F}. Esta ecuación diferencial se llama "la" ecuación de onda en matemáticas, aunque describe sólo una clase muy especial de ondas.

Onda en medio elástico

Considere una onda transversal viajera (que puede ser un pulso) en una cuerda (el medio). Considere que la cadena tiene una sola dimensión espacial. Considere esta onda como viajando

Wavelength λ, se puede medir entre dos puntos correspondientes en una forma de onda

Animación de dos ondas, la onda verde se mueve a la derecha mientras la onda azul se mueve a la izquierda, la amplitud de onda roja neta en cada punto es la suma de las amplitudes de las ondas individuales. Note que f(x,t) + g(x,t) = u(x,t)

• en el x{displaystyle x} dirección en el espacio. Por ejemplo, que el positivo x{displaystyle x} dirección a la derecha, y el negativo x{displaystyle x} dirección a la izquierda.
• con amplitud constante u{displaystyle u}
• con velocidad constante v{displaystyle v}, donde v{displaystyle v} es
  • independiente de longitud de onda (sin dispersión)
  • independiente de la amplitud (media lineal, no no lineal).
• con onda constante, o forma

Esta onda se puede describir mediante las funciones bidimensionales

u()x,t)=F()x− − vt){displaystyle u(x,t)=F(x-vt)} (forma de onda F{displaystyle F} viajar a la derecha)

u()x,t)=G()x+vt){displaystyle u(x,t)=G(x+vt)} (forma de onda G{displaystyle G. viajar a la izquierda)

o, más generalmente, por la fórmula de d'Alembert:

u()x,t)=F()x− − vt)+G()x+vt).{displaystyle u(x,t)=F(x-vt)+G(x+vt).}

representando dos formas de onda componentes F{displaystyle F} y G{displaystyle G. Viajar por el medio en direcciones opuestas. Una representación generalizada de esta onda se puede obtener como la ecuación diferencial parcial

1v2∂ ∂ 2u∂ ∂ t2=∂ ∂ 2u∂ ∂ x2.{displaystyle {frac {1}{2}}{frac {partial ^{2}u}{partial t^{2}}}}={frac {partial ^{2}u}{partial } {partial }u} {f} {f}}}}}} {f}}}}}}}} {f} {f}}} {f}}}}}}}}} {f}}}}}}}}} {f} {f}}}}}}}}}}}}}}}}}}}}}}}}} {f}}} {f}}}}}}}}} {f}}}}}}}}}}} {f} {f} {f}f}}f}}}}}f}}}}}}}}}}f}}}}f}f}}}}}}}}}}}}}}} #

Las soluciones generales se basan en el principio de Duhamel.

Además de las ecuaciones de onda de segundo orden que describen un campo de onda estacionario, la ecuación de onda unidireccional describe la propagación de una sola onda en una dirección definida.

Formas de onda

Sine, cuadrado, triángulo y formas de onda de sierra.

La forma de F en la fórmula de d'Alembert implica el argumento x − vt. Los valores constantes de este argumento corresponden a valores constantes de F, y estos valores constantes ocurren si x aumenta al mismo ritmo que aumenta vt. Es decir, la onda con forma de función F se moverá en la dirección x positiva a una velocidad v (y G se propagará a la misma velocidad en la dirección negativa x).

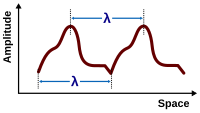
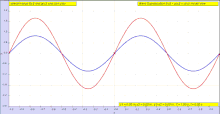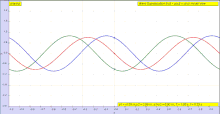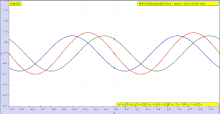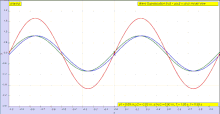
En el caso de una función periódica F con período λ, es decir, F(x + λ − vt) = F(x − vt), la periodicidad de F en el espacio significa que una instantánea de la onda en un momento dado t encuentra que la onda varía periódicamente en el espacio con un período λ (la longitud de onda de la ola). De manera similar, esta periodicidad de F implica también una periodicidad en el tiempo: F(x − v (t + T)) = F(x − vt) proporcionado vT = λ, por lo que una observación de la onda en una ubicación fija x encuentra que la onda ondula periódicamente en el tiempo con un período T = λ /v.

Amplitud y modulación

La modulación de la amplificación se puede lograr mediante f()x,t) = 1.00×sin(2π/0.10×(x1.00×t)) y g()x,t) = 1.00×sin(2π/0.11×(x1.00×t)) sólo el resultado es visible para mejorar la claridad de la forma de onda.

Ilustración de la sobre (la curva roja que varía lentamente) de una onda modulada de amplitud. La curva azul variable rápida es la transportista onda, que está siendo modulada.

La amplitud de una onda puede ser constante (en cuyo caso la onda es una c.w. o onda continua), o puede estar modulada para variar con el tiempo y/o la posición. El contorno de la variación de amplitud se denomina envolvente de la onda. Matemáticamente, la onda modulada se puede escribir en la forma:

u()x,t)=A()x,t)pecado⁡ ⁡ ()kx− − ⋅ ⋅ t+φ φ ),{displaystyle u(x,t)=A(x,t)sin left(kx-omega t+phi right),}

Donde A()x,t){displaystyle A(x, t)} es el sobre de amplitud de la onda, k{displaystyle k} es número de onda y φ φ {displaystyle phi } es fase. Si la velocidad del grupo vg{displaystyle v_{g} (ver abajo) es independiente de longitud de onda, esta ecuación puede ser simplificada como:

u()x,t)=A()x− − vgt)pecado⁡ ⁡ ()kx− − ⋅ ⋅ t+φ φ ),{displaystyle u(x,t)=A(x-v_{g}t)sin left(kx-omega t+phi right),}

mostrando que la envolvente se mueve con la velocidad del grupo y conserva su forma. De lo contrario, en los casos en que la velocidad del grupo varía con la longitud de onda, la forma del pulso cambia de una manera descrita a menudo mediante una ecuación de envolvente.

Velocidad de fase y velocidad de grupo

El cuadrado rojo se mueve con la velocidad de fase, mientras que los círculos verdes se propagan con la velocidad del grupo

Hay dos velocidades asociadas con las ondas, la velocidad de fase y la velocidad de grupo.

La velocidad de fase es la velocidad a la que la fase de la onda se propaga en el espacio: cualquier fase dada de la onda (por ejemplo, la cresta) parecerá viajar a la velocidad de fase. La velocidad de fase se da en términos de la longitud de onda λ (lambda) y el período T como

vp=λ λ T.{displaystyle v_{mathrm {fnK}={fnMicroc {fnMicrosoft} - Sí.

Una ola con las velocidades de grupo y fase va en diferentes direcciones

La velocidad de grupo es una propiedad de las ondas que tienen una envolvente definida, que mide la propagación a través del espacio (es decir, la velocidad de fase) de la forma general de las ondas' amplitudes: modulación o envolvente de la onda.

Ondas especiales

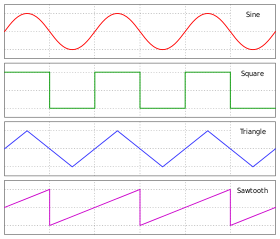
Ondas sinusoidales

Los gráficos de las funciones sine (rojo sólido) y cosine (azul dotado) son sinusoides de diferentes fases

Una onda sine, onda sinusoidal, o simplemente sinusoid es una curva matemática definida en términos de la sine Función trigonométrica, de la cual es el gráfico. Es un tipo de onda continua y también una función periódica lisa. Se produce a menudo en matemáticas, así como en física, ingeniería, procesamiento de señales y muchos otros campos.

Ondas planas

Una onda plana es una especie de onda cuyo valor varía sólo en una dirección espacial. Es decir, su valor es constante en un plano perpendicular a esa dirección. Las ondas planas pueden ser especificadas por un vector de longitud de unidad n^ ^ {displaystyle {hat {n}}} indicando la dirección en que la onda varía, y un perfil de onda que describe cómo la onda varía como una función del desplazamiento a lo largo de esa dirección (n^ ^ ⋅ ⋅ x→ → {displaystyle {hat {n}cdot {vec}}) y tiempo (t{displaystyle t}). Puesto que el perfil de onda sólo depende de la posición x→ → {displaystyle {vec {x}} en la combinación n^ ^ ⋅ ⋅ x→ → {displaystyle {hat {n}cdot {vec}}, cualquier desplazamiento en direcciones perpendiculares a n^ ^ {displaystyle {hat {n}}} no puede afectar el valor del campo.

Las ondas planas se utilizan a menudo para modelar ondas electromagnéticas lejos de una fuente. Para las ondas planas electromagnéticas, los campos eléctricos y magnéticos son transversales a la dirección de propagación y también perpendiculares entre sí.

Ondas estacionarias

Ola de pie. Los puntos rojos representan los nodos de onda

Una onda estacionaria, también conocida como onda estacionaria, es una onda cuya envolvente permanece en una posición constante. Este fenómeno surge como resultado de la interferencia entre dos ondas que viajan en direcciones opuestas.

La suma de dos ondas que se propagan en sentido contrario (de igual amplitud y frecuencia) crea una onda estacionaria. Las ondas estacionarias comúnmente surgen cuando un límite bloquea una mayor propagación de la onda, provocando así la reflexión de la onda y, por lo tanto, introduciendo una onda de contrapropagación. Por ejemplo, cuando se desplaza una cuerda de violín, las ondas transversales se propagan hacia donde la cuerda se mantiene en su lugar en el puente y la tuerca, donde las ondas se reflejan de regreso. En el puente y la tuerca, las dos ondas opuestas están en antifase y se anulan entre sí, produciendo un nodo. A medio camino entre dos nodos hay un antinodo, donde las dos ondas que se propagan en sentido contrario se potencian entre sí al máximo. No hay propagación neta de energía a lo largo del tiempo.

• 

  Ondas de pie unidimensionales; el modo fundamental y los primeros 5 tonos.

• 

  Una onda de pie bidimensional en un disco; este es el modo fundamental.

• 

  Una onda de pie en un disco con dos líneas nodal cruzando en el centro; esto es una sobretonación.

Propiedades físicas

Viga ligera que exhibe reflexión, refracción, transmisión y dispersión al encontrar un prisma

Las olas exhiben comportamientos comunes en una serie de situaciones estándar, por ejemplo:

Transmisión y medios

Las ondas normalmente se mueven en línea recta (es decir, rectilíneamente) a través de un medio de transmisión. Dichos medios pueden clasificarse en una o más de las siguientes categorías:

• A mediano si es finito en extensión, de lo contrario medio sin límites
• A médium lineal si las amplitudes de diferentes ondas en cualquier punto particular en el medio se pueden añadir
• A uniforme medio o medio homogéneo si sus propiedades físicas no cambian en diferentes lugares del espacio
• An medio anisotrópico si una o más de sus propiedades físicas difieren en una o más direcciones
• An medio isotrópico si sus propiedades físicas son igual en todas las direcciones

Absorción

Las ondas generalmente se definen en medios que permiten que la mayor parte o la totalidad de la energía de una onda se propague sin pérdida. Sin embargo, los materiales pueden caracterizarse como "con pérdidas" si extraen energía de una onda, normalmente convirtiéndola en calor. Esto se denomina "absorción". Un material que absorbe la energía de una onda, ya sea en transmisión o reflexión, se caracteriza por un índice de refracción que es complejo. La cantidad de absorción generalmente dependerá de la frecuencia (longitud de onda) de la onda, lo que, por ejemplo, explica por qué los objetos pueden aparecer coloreados.

Reflexión

Cuando una onda golpea una superficie reflectante, cambia de dirección, de modo que el ángulo formado por la onda incidente y la línea normal a la superficie es igual al ángulo formado por la onda reflejada y la misma línea normal.

Refracción

Ola de avión viajando sinusoidal entrando en una región de baja velocidad de onda en un ángulo, lo que ilustra la disminución de longitud de onda y el cambio de dirección (refracción) que resulta.

La refracción es el fenómeno de una onda que cambia su velocidad. Matemáticamente, esto significa que el tamaño de la velocidad de fase cambia. Típicamente, la refracción ocurre cuando una onda pasa de un medio a otro. La cantidad por la cual una onda es refractada por un material está dada por el índice de refracción del material. Las direcciones de incidencia y refracción están relacionadas con los índices de refracción de los dos materiales por la ley de Snell.

Difracción

Una onda exhibe difracción cuando encuentra un obstáculo que dobla la onda o cuando se propaga después de emerger de una abertura. Los efectos de difracción son más pronunciados cuando el tamaño del obstáculo o la abertura es comparable a la longitud de onda de la onda.

Interferencia

Olas idénticas de dos fuentes sometidas a interferencia. Se observa en la parte inferior se ven 5 posiciones donde las olas se añaden en fase, pero entre las cuales están fuera de fase y se cancelan.

Cuando las ondas en un medio lineal (el caso habitual) se cruzan entre sí en una región del espacio, en realidad no interactúan entre sí, sino que continúan como si el otro no estuviera presente. Sin embargo, en cualquier punto en esa región, las cantidades de campo que describen esas ondas se suman según el principio de superposición. Si las ondas son de la misma frecuencia en una relación de fase fija, generalmente habrá posiciones en las que las dos ondas están en fase y sus amplitudes suman, y otras posiciones donde están fuera de fase y sus amplitudes (parcial o totalmente) cancelan. Esto se llama patrón de interferencia.

Polarización

El fenómeno de la polarización surge cuando el movimiento ondulatorio puede ocurrir simultáneamente en dos direcciones ortogonales. Las ondas transversales se pueden polarizar, por ejemplo. Cuando la polarización se usa como descriptor sin calificación, por lo general se refiere al caso especial y simple de polarización lineal. Una onda transversal está polarizada linealmente si oscila en una sola dirección o plano. En el caso de la polarización lineal, suele ser útil añadir la orientación relativa de ese plano, perpendicular a la dirección de desplazamiento, en el que se produce la oscilación, como "horizontal" por ejemplo, si el plano de polarización es paralelo al suelo. Las ondas electromagnéticas que se propagan en el espacio libre, por ejemplo, son transversales; se pueden polarizar mediante el uso de un filtro polarizador.

Las ondas longitudinales, como las ondas sonoras, no presentan polarización. Para estas ondas solo hay una dirección de oscilación, es decir, a lo largo de la dirección de viaje.

Dispersión

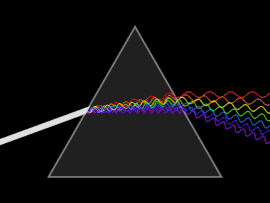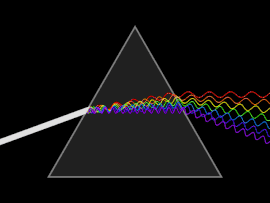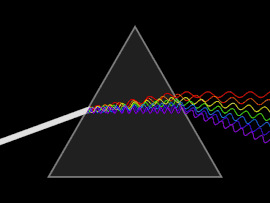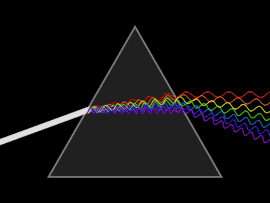
Esquema de luz siendo dispersada por un prisma. Haga clic para ver la animación.

Una onda se dispersa cuando la velocidad de fase o la velocidad de grupo depende de la frecuencia de la onda. La dispersión se ve más fácilmente al dejar pasar la luz blanca a través de un prisma, cuyo resultado es producir el espectro de colores del arco iris. Isaac Newton realizó experimentos con luz y prismas, presentando sus hallazgos en la Óptica (1704) de que la luz blanca consta de varios colores y que estos colores no se pueden descomponer más.

Ondas mecánicas

Ondas en cuerdas

La velocidad de una onda transversal que viaja a lo largo de una cuerda vibrante (v) es directamente proporcional a la raíz cuadrada de la tensión de la cuerda (T) sobre la línea densidad de masa (μ):

v=Tμ μ ,{fnMicroc} {T} {mu}}}}

donde la densidad lineal μ es la masa por unidad de longitud de la cuerda.

Ondas acústicas

Las ondas acústicas o de sonido viajan a una velocidad dada por

v=B*** *** 0,{fnMicroc} {B}{rho _ {0}}}}}

o la raíz cuadrada del módulo de volumen adiabático dividido por la densidad del fluido ambiental (ver velocidad del sonido).

Ondas de agua

• Los pezones en la superficie de un estanque son en realidad una combinación de ondas transversales y longitudinales; por lo tanto, los puntos en la superficie siguen caminos orbitales.
• Sonido: una onda mecánica que se propaga a través de gases, líquidos, sólidos y plasmas;
• Las ondas inerciales, que se producen en los fluidos rotatorios y son restauradas por el efecto Coriolis;
• Olas de superficie marina, que son perturbaciones que se propagan a través del agua.

Ondas sísmicas

Las ondas sísmicas son ondas de energía que viajan a través de las capas de la Tierra y son el resultado de terremotos, erupciones volcánicas, movimientos de magma, grandes deslizamientos de tierra y grandes explosiones provocadas por el hombre que emiten energía acústica de baja frecuencia.

Efecto Doppler

El efecto Doppler (o el desplazamiento Doppler) es el cambio de frecuencia de una onda en relación con un observador que se mueve en relación con la fuente de onda. Lleva el nombre del físico austriaco Christian Doppler, quien describió el fenómeno en 1842.

Ondas de choque

Formación de una onda de choque en un avión.

Una onda de choque es un tipo de perturbación que se propaga. Cuando una onda se mueve más rápido que la velocidad local del sonido en un fluido, es una onda de choque. Como una onda ordinaria, una onda de choque transporta energía y puede propagarse a través de un medio; sin embargo, se caracteriza por un cambio abrupto y casi discontinuo en la presión, la temperatura y la densidad del medio.

Otro

• Olas de tráfico, es decir, propagación de diferentes densidades de vehículos automotores, y así sucesivamente, que se pueden modelar como ondas cinemáticas
• La ola metacrónica se refiere a la aparición de una ola de viaje producida por acciones secuenciales coordinadas.

Ondas electromagnéticas

Una onda electromagnética consta de dos ondas que son oscilaciones de los campos eléctrico y magnético. Una onda electromagnética viaja en una dirección que forma ángulos rectos con la dirección de oscilación de ambos campos. En el siglo XIX, James Clerk Maxwell demostró que, en el vacío, los campos eléctrico y magnético satisfacen la ecuación de onda ambos con una velocidad igual a la de la luz. De ahí surgió la idea de que la luz es una onda electromagnética. Las ondas electromagnéticas pueden tener diferentes frecuencias (y, por lo tanto, longitudes de onda), dando lugar a varios tipos de radiación, como ondas de radio, microondas, infrarrojos, luz visible, ultravioleta, rayos X y rayos Gamma.

Ondas mecánicas cuánticas

Ecuación de Schrödinger

La ecuación de Schrödinger describe el comportamiento ondulatorio de las partículas en la mecánica cuántica. Las soluciones de esta ecuación son funciones de onda que pueden usarse para describir la densidad de probabilidad de una partícula.

Ecuación de Dirac

La ecuación de Dirac es una ecuación de onda relativista que detalla las interacciones electromagnéticas. Las ondas de Dirac explicaron los detalles finos del espectro del hidrógeno de una manera completamente rigurosa. La ecuación de onda también implicaba la existencia de una nueva forma de materia, antimateria, previamente insospechada e inobservada y que fue confirmada experimentalmente. En el contexto de la teoría cuántica de campos, la ecuación de Dirac se reinterpreta para describir los campos cuánticos correspondientes a spin-1⁄2 partículas.

Un paquete de onda propagante; en general, el sobre del paquete de onda se mueve a una velocidad diferente que las ondas constitutivas.

Olas de De Broglie

Louis de Broglie postuló que todas las partículas con momento tienen una longitud de onda

λ λ =hp,{displaystyle lambda = {h}{p}}

donde h es la constante de Planck y p es la magnitud del momento de la partícula. Esta hipótesis estaba en la base de la mecánica cuántica. Hoy en día, esta longitud de onda se llama longitud de onda de De Broglie. Por ejemplo, los electrones en una pantalla CRT tienen una longitud de onda de De Broglie de aproximadamente 10⁻¹³ m.

Una onda que representa tal partícula que viaja en la dirección k se expresa mediante la función de onda de la siguiente manera:

↑ ↑ ()r,t=0)=Aeik⋅ ⋅ r,{displaystyle psi (mathbf {r},t=0)=Ae^{imathbf {kcdot r},}

donde la longitud de onda está determinada por el vector de onda k como:

λ λ =2π π k,{displaystyle lambda ={frac {2pi}{k}}}

y el impulso por:

p=▪ ▪ k.{displaystyle mathbf {p} =hbar mathbf {k}

Sin embargo, una onda como esta con una longitud de onda definida no está localizada en el espacio y, por lo tanto, no puede representar una partícula localizada en el espacio. Para localizar una partícula, de Broglie propuso una superposición de diferentes longitudes de onda que oscilan alrededor de un valor central en un paquete de ondas, una forma de onda que se usa a menudo en la mecánica cuántica para describir la función de onda de una partícula. En un paquete de ondas, la longitud de onda de la partícula no es precisa y la longitud de onda local se desvía a ambos lados del valor de la longitud de onda principal.

Al representar la función de onda de una partícula localizada, el paquete de ondas a menudo se considera que tiene una forma gaussiana y se denomina paquete de ondas gaussianas. Los paquetes de ondas gaussianas también se utilizan para analizar las ondas de agua.

Por ejemplo, una función de onda gaussiana ψ podría tomar la forma:

↑ ↑ ()x,t=0)=Aexp⁡ ⁡ ()− − x22σ σ 2+ik0x),{displaystyle psi (x,,t=0)=Aexp left(-{frac {x^{2}{2sigma ^{2}}}+ik_{0}xright),}

en algún momento inicial t = 0, donde la longitud de onda central está relacionada con el vector de onda central k₀ como λ ₀ = 2π / k₀. Es bien sabido por la teoría del análisis de Fourier, o por el principio de incertidumbre de Heisenberg (en el caso de la mecánica cuántica) que se necesita un rango estrecho de longitudes de onda para producir un paquete de ondas localizado, y cuanto más localizada es la envolvente, mayor es la longitud de onda. propagarse en las longitudes de onda requeridas. La transformada de Fourier de una gaussiana es en sí misma una gaussiana. Dada la Gaussiana:

f()x)=e− − x2/()2σ σ 2),{displaystyle f(x)=e^{-x^{2}/left(2sigma ^{2}right)}}

la transformada de Fourier es:

f~ ~ ()k)=σ σ e− − σ σ 2k2/2.{displaystyle {tilde {f}(k)=sigma e^{-sigma ^{2}k^{2}/2}

La gaussiana en el espacio por lo tanto se compone de ondas:

f()x)=12π π ∫ ∫ − − JUEGO JUEGO JUEGO JUEGO f~ ~ ()k)eikxdk;{\fnMicrosoft Sans Serif}int _{infty }infty {cHFF}(k)e^{ikx} dk;}

es decir, un número de ondas de longitudes de onda λ tal que kλ = 2 π.

El parámetro σ decide la dispersión espacial de la Gaussiana a lo largo del eje x, mientras que la transformada de Fourier muestra una dispersión en el vector de onda k determinada por 1/σ. Es decir, cuanto menor sea la extensión en el espacio, mayor será la extensión en k y, por lo tanto, en λ = 2π/k.

Animación mostrando el efecto de una onda gravitacional multipolarizada en un anillo de partículas de prueba

Ondas de gravedad

Las ondas de gravedad son ondas generadas en un medio fluido o en la interfaz entre dos medios cuando la fuerza de la gravedad o la flotabilidad intenta restablecer el equilibrio. Una onda en un estanque es un ejemplo.

Ondas gravitacionales

Las ondas gravitacionales también viajan por el espacio. La primera observación de ondas gravitacionales se anunció el 11 de febrero de 2016. Las ondas gravitacionales son perturbaciones en la curvatura del espacio-tiempo, predichas por la teoría de la relatividad general de Einstein.