Octómino

Un octominó (u octominó 8) es un poliominó de orden 8, es decir, un polígono en el plano formado por 8 cuadrados de igual tamaño conectados borde con borde. Cuando las rotaciones y las reflexiones no se consideran formas distintas, hay 369 octominós libres diferentes. Cuando las reflexiones se consideran distintas, hay 704 octominós unilaterales. Cuando las rotaciones también se consideran distintas, hay 2725 octominós fijos.

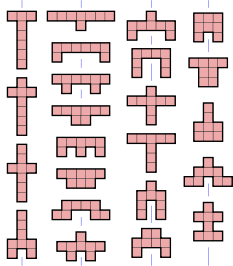
La figura muestra todos los octominós libres posibles, coloreados según sus grupos de simetría:

• 316 octominos no tienen simetría. Su grupo de simetría consiste sólo en el mapeo de identidad.
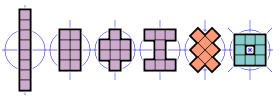
• 23 octominos (rojo colorado) tienen un eje de simetría de reflexión alineado con las redes. Su grupo de simetría tiene dos elementos, la identidad y la reflexión en una línea paralela a los lados de los cuadrados.

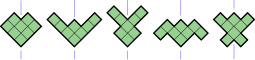
• 5 octominos (verde verde) tienen un eje de simetría de reflexión a 45° a las líneas de red. Su grupo de simetría tiene dos elementos, la identidad y una reflexión diagonal.

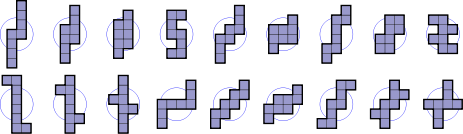
• 18 octominos (azul colorado) tienen simetría de puntos, también conocida como simetría rotacional del orden 2. Su grupo de simetría tiene dos elementos, la identidad y la rotación de 180°.

• 1 octomino (color amarillo colorado) tiene simetría rotacional del orden 4. Su grupo de simetría tiene cuatro elementos, la identidad y las rotaciones 90°, 180° y 270°.

• 4 octominos (color púrpura) tienen dos ejes de simetría de reflexión, ambos alineados con las redes. Su grupo de simetría tiene cuatro elementos, la identidad, dos reflexiones y la rotación de 180°. Es el grupo dihedral del orden 2, también conocido como el grupo Klein cuatro.
• 1 octomino (naranja colorada) tiene dos ejes de simetría de reflexión, ambos alineados con las diagonales. Su grupo de simetría es también el grupo dihedral del orden 2 con cuatro elementos.
• 1 octomino (cian colorado) tiene cuatro ejes de simetría de reflexión, alineados con las redes y las diagonales, y simetría rotacional del orden 4. Su grupo de simetría, el grupo dihedral del orden 4, tiene ocho elementos.

El conjunto de los octominós es el conjunto poliominó más bajo en el que se cumplen las ocho simetrías posibles. El siguiente conjunto superior con esta propiedad es el conjunto dodecomino (12-ominó).

Si las reflexiones de un octominó se consideran distintas, como ocurre con los octominós unilaterales, entonces las categorías primera, cuarta y quinta mencionadas anteriormente duplican su tamaño, lo que da como resultado 335 octominós adicionales para un total de 704. Si las rotaciones también se consideran distintas, entonces los octominós de la primera categoría cuentan ocho veces, los de las siguientes tres categorías cuentan cuatro veces, los de las categorías cinco a siete cuentan dos veces y el último octominó cuenta solo una vez. Esto da como resultado 316 × 8 + (23+5+18) × 4 + (1+4+1) × 2 + 1 = 2725 octominós fijos.

De los 369 octominós libres, 320 satisfacen el criterio de Conway y 23 más pueden formar un parche que satisfaga el criterio. Los otros 26 octominós (incluidos los 6 con agujeros) no pueden teselar el plano.

Dado que 6 de los octominós libres tienen un agujero, es fácil demostrar que el conjunto completo de octominós no se puede empaquetar en un rectángulo y que no todos los octominós se pueden colocar en mosaico.