Octaedro truncado

ImprimirCitar

Arquitecto sólido

Truncado octaedro
(Haga clic aquí para el modelo giratorio)
Tipo	Arquitecto sólido Uniform polyhedron
Elementos	F = 14, E = 36, V = 24 (χ = 2)
Caras por lados	6{4}+8{6}
Notación de Conway	tO bT
Símbolos de Schläfli	t{3,4} o $t{begin{Bmatrix}3\3end{Bmatrix}}$
Símbolos de Schläfli	t_0,1{3,4} o t_0,1,2{3,3}
Signatura Wythoff	2 4 Silencio 3 3 3 2
Coxeter diagrama
Grupo de Symmetry	Oh, B₃, [4,3], (432), orden 48 Th, [3,3] y (332), orden 24
Grupo de rotación	O, [4,3]⁺, (432), orden 24
Ángulo Dihedral	4-6: arccos(−1/√3) = 125°15′51′ 6-6: arccos(−1/3) = 109°28′16′′
Referencias	U₀₈, C₂₀, W₇
Propiedades	Convexo semiregular paraleloohedron permutohedron zonohedron
Caras de colores	4.6.6 (Vertex figure)
Tetrakis hexahedron (poliedro dual)	Cifras netas

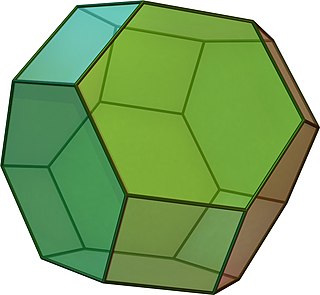
En geometría, el octaedro truncado es el sólido de Arquímedes que surge de un octaedro regular quitando seis pirámides, una en cada uno de los vértices del octaedro. El octaedro truncado tiene 14 caras (8 hexágonos regulares y 6 cuadrados), 36 aristas y 24 vértices. Dado que cada una de sus caras tiene simetría puntual, el octaedro truncado es un 6-zonoedro. También es el poliedro de Goldberg G_IV(1,1), que contiene caras cuadradas y hexagonales. Al igual que el cubo, puede teselar (o "empacar") un espacio tridimensional, como un permutoedro.

Did you mean:

The truncated octahedron was called the n#34;mecon" by Buckminster Fuller.

Su poliedro dual es el tetrakis hexaedro. Si el octaedro truncado original tiene una longitud de arista unitaria, su tetrakis hexaedro dual tiene longitudes de arista 9/8√2 y 3/2√2.

Construcción

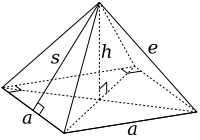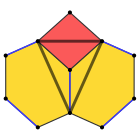
Un octaedro truncado se construye a partir de un octaedro regular con una longitud de lado de 3a mediante la eliminación de seis pirámides cuadradas rectas, una de cada punto. Estas pirámides tienen tanto la longitud del lado de la base (a) como la longitud del lado lateral (e) de a, para formar triángulos equiláteros. El área base es entonces a². Tenga en cuenta que esta forma es exactamente similar a la mitad de un octaedro o Johnson sólido J₁.

De las propiedades de las pirámides cuadradas, ahora podemos encontrar la altura inclinada, s, y la altura, h, de la pirámide:

{displaystyle {begin{aligned}h&={sqrt {e^{2}-{tfrac {1}{2}}a^{2}}}&&={tfrac {1}{sqrt {2}}}a\s&={sqrt {h^{2}+{tfrac {1}{4}}a^{2}}}&&={sqrt {{tfrac {1}{2}}a^{2}+{tfrac {1}{4}}a^{2}}}&&={tfrac {sqrt {3}}{2}}aend{aligned}}}

El volumen, V, de la pirámide viene dado por:

{displaystyle V={tfrac {1}{3}}a^{2}h={tfrac {sqrt {2}}{6}}a^{3}}

Debido a que seis pirámides se eliminan por truncamiento, hay un volumen perdido total de √2a³.

Proyecciones ortogonales

El octaedro truncado tiene cinco proyecciones ortogonales especiales, centradas, en un vértice, en dos tipos de aristas y dos tipos de caras: hexagonal y cuadrada. Los dos últimos corresponden a los planos B₂ y A₂ de Coxeter.

Proyecciones ortogonales
Centrado por	Vertex	Edge 4-6	Edge 6-6	Cara Plaza	Cara Hexagon
Sólido
Wireframe
Doble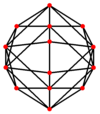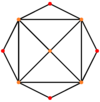
Projective simetría	[2]	[2]	[2]	[4]	[6]

Alicatados esféricos

El octaedro truncado también puede representarse como un mosaico esférico y proyectarse en el plano a través de una proyección estereográfica. Esta proyección es conforme, preservando ángulos pero no áreas o longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.

Proyección ortográfica	Proyecciones estereográficas
	cuadrado centrado	hexágono centrado

Coordenadas


Proyección ortogonal en caja atada (±2,±2,±2)	Octaedro truncado con hexágonos reemplazados por 6 triángulos coplanar. Hay 8 nuevos vértices en: (±1,±1,±1).	Octaedro truncado subdividido como un triacontahedro rhombic topológico

Todas las permutaciones de (0, ±1, ±2) son coordenadas cartesianas de los vértices de un octaedro truncado de longitud de arista a = √2 con centro en el origen. Los vértices son así también las esquinas de 12 rectángulos cuyos lados largos son paralelos a los ejes de coordenadas.

Los vectores de borde tienen coordenadas cartesianas (0, ±1, ±1) y permutaciones de estas. Las caras normales (productos cruzados normalizados de aristas que comparten un vértice común) de las 6 caras cuadradas son (0, 0, ±1), (0, ±1, 0) y (±1, 0, 0). Las caras normales de las 8 caras hexagonales son (±1/√3, ±1/√3, ±1/√3). El producto escalar entre pares de dos caras normales es el coseno del ángulo diedro entre caras adyacentes, ya sea −1/3 o −1/√3. El ángulo diedro es de aproximadamente 1,910633 radianes (109,471° OEIS: A156546) en los bordes compartidos por dos hexágonos o 2,186276 radianes (125,263° OEIS: A195698) en los bordes compartidos por un hexágono y un cuadrado.

Disección

Did you mean:

The truncated octahedron can be dissected into a central octahedron, surrounded by 8 triangular cupola on each face, and 6 square pyramids above the vertices.

Quitar el octaedro central y 2 o 4 cúpulas triangulares crea dos toroides de Stewart, con simetría diédrica y tetraédrica:

Género 2	Género 3
D3d, [2]⁺,6], (2*3), orden 12	Td, [3,3], (*332), orden 24

Permutoedro

El octaedro truncado también se puede representar mediante coordenadas aún más simétricas en cuatro dimensiones: todas las permutaciones de (1, 2, 3, 4) forman los vértices de un octaedro truncado en el subespacio tridimensional x + y + z + w = 10. Por lo tanto, el octaedro truncado es el permutaedro de orden 4: cada vértice corresponde a una permutación de (1, 2, 3, 4) y cada arista representa un único intercambio por pares de dos elementos.

Área y volumen

El área superficial S y el volumen V de un octaedro truncado de longitud de arista a son:

{displaystyle {begin{aligned}S&=left(6+12{sqrt {3}}right)a^{2}&&approx 26.784,6097a^{2}\V&=8{sqrt {2}}a^{3}&&approx 11.313,7085a^{3}.end{aligned}}}

Colores uniformes

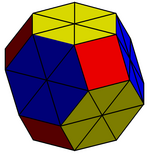
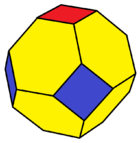
Hay dos coloraciones uniformes, con simetría tetraédrica y simetría octaédrica, y dos coloraciones 2-uniformes con simetría diédrica como un antiprisma triangular truncado. Los nombres constructivos se dan para cada uno. Su notación de poliedro de Conway se da entre paréntesis.

1-uniform		2-uniform
[4,3], (*432) Orden 48	Td, [3,3], (*332) Orden 24	D4h, [4,2], (*422) Orden 16	D3d, [2]⁺,6], (2*3) Orden 12
122 colores	123 para colorear	122 & 322 colores	122 & 123 colorantes
Truncado octaedro (tO)	Bevelled tetrahedron bT)	Bipirámide cuadrado truncado (tdP4)	Anticipo triangular truncado (tA3)

Química

El octaedro truncado existe en la estructura de los cristales de faujasita.

Ocultación de datos

El octaedro truncado (de hecho, el octaedro truncado generalizado) aparece en el análisis de errores de la modulación del índice de cuantificación (QIM) junto con la codificación de repetición.

Poliedros relacionados

El octaedro truncado pertenece a una familia de poliedros uniformes relacionados con el cubo y el octaedro regular.

Uniform octaedral polyhedra
Simetría: [4,3], (*432)							[4,3]⁺ (432)	[1]⁺,4,3] = [3,3] (*332)		[3]⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1.1}	t{3,4} t{3^1.1}	{3,4} {3}^1.1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	S{3,4} s{3^1.1}

		=	=	=				= o	= o	=

Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

También existe como el omnitruncado de la familia de los tetraedros:

Familia de polihedra de tetraedral uniforme
Simetría: [3,3], (*332)							[3,3]⁺, (332)


{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duals to uniform polyhedra

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3

Mutaciones de simetría

n32 mutación de simetría de los revestimientos omnímicos: 4.6.2n* v t e
Sym. *n32 [n,3]	Spherical				Euclid.	Hiperb compacto.		Paraco.	Hiperbólico no consumado
Sym. *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Gráficos
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duales
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

*n2 mutaciones simétricas de los revestimientos omnímicos: 4.2n.2n v t e
Simmetría *n2 [n,n]	Spherical		Euclidean	Hiperbólico compacto				Paracomp.
Simmetría *n2 [n,n]	*222 [2,2]	*332 [3,3]	*442 [4,4]	*552 [5,5]	*662 [6,6]	*772 [7,7]	*882 [8,8]...	* [viejos]
Gráfico
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4. Voluntad.
Doble
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.

Este poliedro es miembro de una secuencia de patrones uniformes con figura de vértice (4.6.2p) y el diagrama Coxeter-Dynkin . Para pLos miembros de la secuencia son polihedra omnitruncada (zonohedra), que se muestra a continuación como revestimientos esféricos. Para pØ 6, son tilings del plano hiperbólico, empezando por el azulejo triheptagonal truncado.

El octaedro truncado está relacionado topológicamente como parte de una secuencia de poliedros uniformes y mosaicos con figuras de vértice n.6.6, que se extienden hacia el plano hiperbólico:

*n32 mutación simetría de los azulejos truncados: n.6.6 v t e
Sym. *n42 [n,3]	Spherical				Euclid.	Compacto		Parac.	Hiperbólico no consumado
Sym. *n42 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Truncado cifras
Config.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	JUEGO.6	12i.6.6	9i.6.6	6i.6.6
N-kis cifras
Config.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V dieta.6.6	V12i.6.6	V9i.6.6	V6i.6.6

El octaedro truncado está relacionado topológicamente como parte de una secuencia de poliedros uniformes y mosaicos con figuras de vértice 4.2n.2n, extendiéndose hacia el plano hiperbólico:

*n42 mutación simetría de los revestimientos truncados: 4.2n.2n v t e
Simmetría *n42 [n,4]	Spherical		Euclidean	Hiperbólico compacto				Paracomp.
Simmetría *n42 [n,4]	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	* [∞,4]
Truncado cifras
Config.	4.4.4	4.6.6	4.8.8	4.10.10	4.12.12	4.14.14	4.16.16	4. Voluntad.
N-kis cifras
Config.	V4.4.4	V4.6.6	V4.8.8	V4.10	V4.12.12	V4.14.14	V4.16.16	V4.∞.

Polítopos relacionados

Did you mean:

The truncated octahedron (truncated cube), is first in a sequence of truncated hypercubes:

Hipercubos bitruncados
Imagen							...
Nombre	Cubo bitruncado	Tesseract bitruncado	Bitruncated 5-cube	Bitruncated 6-cube	Bitruncado 7-cubo	Bitruncated 8-cube
Coxeter
Vertex figure	()v{ }	{}v{}	{}v{3}	{}v{3,3}	{}v{3,3,3}	{}v{3,3,3,3,3}

Es posible cortar un teseracto por un hiperplano de modo que su sección transversal cortada sea un octaedro truncado.

Teselados

El octaedro truncado existe en tres panales uniformes convexos diferentes (teselados que llenan el espacio):

Bitruncado cúbico	Cantitruncado cúbico	Truncado alternado cúbico

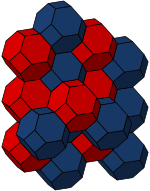El panal cúbico bitruncado transitivo de células también se puede ver como la teselación de Voronoi de la red cúbica centrada en el cuerpo. El octaedro truncado es uno de los cinco paraleloedros primarios tridimensionales.

Objetos

Las redes de gimnasia Jungle suelen incluir octahedra truncada.

antigua Morir chino
escultura en Bonn
Rubik's Cube variante
modelo hecho con conjunto de construcción Polydron
Cristal de pirita

Gráfico octaédrico truncado

En el campo matemático de la teoría de grafos, un grafo octaédrico truncado es el gráfico de vértices y aristas del octaedro truncado. Tiene 24 vértices y 36 aristas, y es un grafo de Arquímedes cúbico. Tiene grosor de libro 3 y número de cola 2.

Como gráfico cúbico hamiltoniano, se puede representar mediante la notación LCF de varias formas: [3, −7, 7, −3]⁶, [5, −11, 11, 7, 5, −5, −7, −11, 11, −5, −7, 7]² y [−11, 5, −3, −7, −9, 3, −5, 5, −3, 9, 7, 3, −5, 11, −3, 7, 5, −7, −9, 9, 7, −5, −7, 3].

Contenido relacionado

Más resultados...

Octaedro truncado

Construcción

Proyecciones ortogonales

Alicatados esféricos

Coordenadas

Disección

Permutoedro

Área y volumen

Colores uniformes

Química

Ocultación de datos

Poliedros relacionados

Mutaciones de simetría

Polítopos relacionados

Teselados

Objetos

Gráfico octaédrico truncado

Contenido relacionado

Mikio Sato

Independencia algebraica

Número (desambiguación)