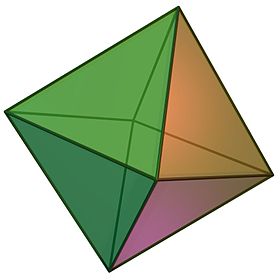
Octaedro

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Poliedro con ocho caras triangulares

Octaedro ordinario
(Haga clic aquí para el modelo giratorio)
Tipo	sólido platónico
Elementos	F = 8, E = 12 V = 6 (χ = 2)
Caras por lados	8{3}
Notación de Conway	O aT
Símbolos de Schläfli	{3,4}
Símbolos de Schläfli	o ${begin{Bmatrix}3\3end{Bmatrix}}$ {}+{}=3 {}
Configuración facial	V4.4.4
Signatura Wythoff	4 Silencio 2 3
Coxeter diagrama
Simmetría	Oh, BC₃, [4,3], (*432)
Grupo de rotación	O, [4,3]⁺, (432)
Referencias	U₀₅, C₁₇, W₂
Propiedades	regular, convexdeltahedron, Hanner politope
Ángulo Dihedral	109.47122° = arcos (−1.3)
3.3.3.3 (Vertex figure)	Cube (poliedro dual)
Cifras netas

Modelo 3D de octaedro regular.

En geometría, un octaedro (plural: octaedros, octaedros) es un poliedro de ocho caras. El término se usa más comúnmente para referirse al octaedro regular, un sólido platónico compuesto por ocho triángulos equiláteros, cuatro de los cuales se encuentran en cada vértice.

Un octaedro regular es el poliedro dual de un cubo. Es un tetraedro rectificado. Es una bipirámide cuadrada en cualquiera de las tres orientaciones ortogonales. También es un antiprisma triangular en cualquiera de las cuatro orientaciones.

Un octaedro es el caso tridimensional del concepto más general de un politopo cruzado.

Un octaedro regular es una bola de 3 en la métrica de Manhattan (ℓ1).

Octaedro regular

Dimensiones

Si la longitud de la arista de un octaedro regular es a, el radio de una esfera circunscrita (una que toca el octaedro en todos los vértices) es

{displaystyle r_{u}={frac {sqrt {2}}{2}}aapprox 0.707cdot a}

y el radio de una esfera inscrita (tangente a cada una de las caras del octaedro) es

{displaystyle r_{i}={frac {sqrt {6}}{6}}aapprox 0.408cdot a}

mientras que el radio medio, que toca el centro de cada borde, es

{displaystyle r_{m}={tfrac {1}{2}}a=0.5cdot a}

Proyecciones ortogonales

El octaedro tiene cuatro proyecciones ortogonales especiales, centradas, sobre una arista, vértice, cara y normal a una cara. El segundo y el tercero corresponden a los planos B₂ y A₂ de Coxeter.

Proyecciones ortogonales
Centrado por	Edge	Cara Normal	Vertex	Cara
Imagen
Projective simetría	[2]	[2]	[4]	[6]

Alicatados esféricos

El octaedro también puede representarse como un mosaico esférico y proyectarse en el plano a través de una proyección estereográfica. Esta proyección es conforme, preservando ángulos pero no áreas o longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.

Proyección ortográfica	Proyección estereográfica

Coordenadas cartesianas

Un octaedro con longitud de arista √2 se puede colocar con su centro en el origen y sus vértices en los ejes de coordenadas; las coordenadas cartesianas de los vértices son entonces

(±1, 0, 0);

(0, ±1, 0);

(0, 0, ±1).

En un sistema de coordenadas cartesianas x–y–z, el octaedro con coordenadas centrales (a, b, c) y el radio r es el conjunto de todos los puntos (x, y, z) tal que

left|x-aright|+left|y-bright|+left|z-cright|=r.

Área y volumen

El área superficial A y el volumen V de un octaedro regular de longitud de arista a son:

A=2{sqrt {3}}a^{2}approx 3.464a^{2}

V={frac {1}{3}}{sqrt {2}}a^{3}approx 0.471a^{3}

Por lo tanto, el volumen es cuatro veces mayor que el de un tetraedro regular con la misma longitud de arista, mientras que el área de la superficie es el doble (porque tenemos 8 en lugar de 4 triángulos).

Si se ha alargado un octaedro para que obedezca la ecuación

left|{frac {x}{x_{m}}}right|+left|{frac {y}{y_{m}}}right|+left|{frac {z}{z_{m}}}right|=1,

las fórmulas para el área de la superficie y el volumen se expanden para convertirse en

A=4,x_{m},y_{m},z_{m}times {sqrt {{frac {1}{x_{m}^{2}}}+{frac {1}{y_{m}^{2}}}+{frac {1}{z_{m}^{2}}}}},

V={frac {4}{3}},x_{m},y_{m},z_{m}.

Además, el tensor de inercia del octaedro estirado es

{displaystyle I={begin{bmatrix}{frac {1}{10}}m(y_{m}^{2}+z_{m}^{2})&0&0\0&{frac {1}{10}}m(x_{m}^{2}+z_{m}^{2})&0\0&0&{frac {1}{10}}m(x_{m}^{2}-y_{m}^{2})end{bmatrix}}.}

Estos se reducen a las ecuaciones para el octaedro regular cuando

x_{m}=y_{m}=z_{m}=a,{frac {sqrt {2}}{2}}.

Relaciones geométricas

Usando la nomenclatura estándar para los sólidos de Johnson, un octaedro se llamaría bipirámide cuadrada.

Doble

El octaedro es el poliedro dual del cubo.

Si un octaedro de longitud de borde ${displaystyle =a}$ se inscribe en un cubo, luego la longitud de un borde del cubo ${displaystyle ={sqrt {2}}a}$ .

Estelación

El octaedro representa la intersección central de dos tetrahedra

El interior del compuesto de dos tetraedros duales es un octaedro, y este compuesto, llamado stella octangula, es su primera y única estelación. En consecuencia, un octaedro regular es el resultado de cortar de un tetraedro regular, cuatro tetraedros regulares de la mitad del tamaño lineal (es decir, rectificar el tetraedro). Los vértices del octaedro se encuentran en los puntos medios de las aristas del tetraedro y, en este sentido, se relaciona con el tetraedro de la misma manera que el cuboctaedro y el icosidodecaedro se relacionan con los otros sólidos platónicos.

Octaedro chato

También se pueden dividir las aristas de un octaedro en la proporción de la media áurea para definir los vértices de un icosaedro. Esto se hace colocando primero vectores a lo largo de las aristas del octaedro de modo que cada cara esté delimitada por un ciclo, y luego dividiendo de manera similar cada arista en la media áurea a lo largo de la dirección de su vector. Hay cinco octaedros que definen cualquier icosaedro dado de esta manera, y juntos definen un compuesto regular. Un icosaedro producido de esta manera se llama octaedro chato.

Teselados

Los octaedros y los tetraedros se pueden alternar para formar un teselado uniforme de vértices, aristas y caras. Este y el teselado regular de cubos son los únicos panales uniformes de este tipo en el espacio tridimensional.

Ortosquema característico

Como todos los politopos convexos regulares, el octaedro se puede dividir en un número entero de ortosquemas disjuntos, todos con la misma forma característica del politopo. El ortosquema característico de un politopo es una propiedad fundamental porque el politopo es generado por reflexiones en las facetas de su ortosquema. El ortosquema se presenta en dos formas quirales que son imágenes especulares entre sí. El ortosquema característico de un poliedro regular es un tetraedro irregular cuadrirrectangular.

Las caras del tetraedro característico del octaedro se encuentran en los planos de simetría del espejo del octaedro. El octaedro es único entre los sólidos platónicos por tener un número par de caras que se encuentran en cada vértice. En consecuencia, es el único miembro de ese grupo que posee, entre sus planos especulares, algunos que no pasan por ninguna de sus caras. El grupo de simetría del octaedro se denota como B3. El octaedro y su politopo dual, el cubo, tienen el mismo grupo de simetría pero tetraedros característicos diferentes.

El característica tetraedro del octaedro regular se puede encontrar por una disección canónica del octaedro regular que lo subdivide en 48 de estos ortoscopios característicos rodeando el centro del octaedro. Tres ortosquemas zurdos y tres ortomas de mano derecha se encuentran en cada uno de los ocho rostros del octaedro, los seis ortomas formando colectivamente un tetraedro trirectangular: una pirámide triangular con la cara del octaedro como su base equilateral, y su ápice de cubo en el centro del octaedro.

Características del octaedro regular
	borde	arc		dihedral
l	$2$	90°	${tfrac {pi }{2}}$	109°28′	${displaystyle pi -2{text{𝟁}}}$

χ	${displaystyle {sqrt {tfrac {4}{3}}}approx 1.155}$	54°44′8′′	${displaystyle {tfrac {pi }{2}}-{text{𝜿}}}$	90°	${tfrac {pi }{2}}$
φ	$1$	45°	$tfrac{pi}{4}$	60°	${tfrac {pi }{3}}$
↑	${displaystyle {sqrt {tfrac {1}{3}}}approx 0.577}$	35°15′′	${displaystyle {text{𝜿}}}$	45°	$tfrac{pi}{4}$

${displaystyle _{0}R/l}$	$sqrt{2} approx 1.414$
${displaystyle _{1}R/l}$	$1$
${displaystyle _{2}R/l}$	${displaystyle {sqrt {tfrac {2}{3}}}approx 0.816}$

Si el octaedro tiene longitud de borde l = 2, su característica tetraedro seis bordes tienen longitudes ${displaystyle {sqrt {tfrac {4}{3}}}}$ , $1$ , ${displaystyle {sqrt {tfrac {1}{3}}}}$ (la cara del triángulo derecho exterior, la triángulo característico χ, φ, ↓ del octaedro), más ${sqrt {2}}$ , $1$ , ${displaystyle {sqrt {tfrac {2}{3}}}}$ (edges that are the característico radii del octaedro). El camino de 3 pasos a lo largo de los bordes ortogonales del ortoscopio es $1$ , ${displaystyle {sqrt {tfrac {1}{3}}}}$ , ${displaystyle {sqrt {tfrac {2}{3}}}}$ , primero desde un vértice de octaedro a un centro de borde de octaedro, luego girando 90° a un centro facial de octaedro, luego girando 90° al centro de octaedro. El ortoscheme tiene cuatro caras de triángulo derecho diferentes. La cara exterior es un triángulo 90-60-30 que es una sexta parte de una cara de octaedro. Las tres caras interiores al octaedro son: un triángulo 45-90-45 con bordes $1$ , ${sqrt {2}}$ , $1$ , un triángulo derecho con bordes ${displaystyle {sqrt {tfrac {1}{3}}}}$ , $1$ , ${displaystyle {sqrt {tfrac {2}{3}}}}$ , y un triángulo derecho con bordes ${displaystyle {sqrt {tfrac {4}{3}}}}$ , ${sqrt {2}}$ , ${displaystyle {sqrt {tfrac {2}{3}}}}$ .

Topología

El octaedro tiene 4 conexiones, lo que significa que se necesita quitar cuatro vértices para desconectar los vértices restantes. Es uno de los cuatro poliedros bien cubiertos simpliciales conectados en 4, lo que significa que todos los conjuntos independientes máximos de sus vértices tienen el mismo tamaño. Los otros tres poliedros con esta propiedad son la bipirámide pentagonal, el disfenoide chato y un poliedro irregular de 12 vértices y 20 caras triangulares.

Redes

El octaedro regular tiene once arreglos de redes.

Fetado

El tetrahemihexaedro uniforme es un facetado de simetría tetraédrica del octaedro regular, que comparte disposición de aristas y vértices. Tiene cuatro de las caras triangulares y 3 cuadrados centrales.

Octahedron	Tetrahemihexahedron

Colores uniformes y simetría

Hay 3 colores uniformes del octaedro, nombrados por los colores de las caras triangulares que giran alrededor de cada vértice: 1212, 1112, 1111.

El grupo de simetría del octaedro es O_h, de orden 48, el grupo hiperoctaédrico tridimensional. Los subgrupos de este grupo incluyen D_3d (orden 12), el grupo de simetría de un antiprisma triangular; D_4h (orden 16), el grupo de simetría de una bipirámide cuadrada; y T_d (orden 24), el grupo de simetría de un tetraedro rectificado. Estas simetrías se pueden enfatizar mediante diferentes colores de las caras.

Nombre	Octahedron	Tetraedro rectificado (Tetratetrahedron)	Antiprismos triangular	Bipyramid cuadrado	Fusil Rhombic
Imagen (coloración facial)	(1111)	(1212)	(1112)	(1111)	(1111)
Coxeter diagrama		=
Símbolo Schläfli	{3,4}	r{3,3}	S{2,6} sr{2,3}	ft{2,4} {} + {4}	ftr{2,2} {} + {} + {}
Signatura Wythoff	4 Silencio 3 2	2 Silencio 4 3	2 Silencio 6 2 TENIDA 2 3 2
Simmetría	O_h, [4,3], (*432)	T_d, [3,3], (*332)	D_3d, [2]⁺,6], (2*3) D₃[2,3]⁺, (322)	D_4h, [2,4], (*422)	D_2h, [2,2], (*222)
Orden	48	24	12 6	16	8

Octaedros irregulares

Los siguientes poliedros son combinatoriamente equivalentes al poliedro regular. Todos tienen seis vértices, ocho caras triangulares y doce aristas que se corresponden uno por uno con las características de un octaedro regular.

Antiprismos triangulares: Dos caras son equiláteros, se encuentran en planos paralelos, y tienen un eje común de simetría. Los otros seis triángulos son isosceles.
Bipirámides tetragonales, en las que al menos uno de los cuadriláteros ecuatoriales se encuentra en un plano. El octaedro regular es un caso especial en el que los tres cuadriláteros son cuadrados planificados.
Schönhardt polihedron, un poliedro no convexo que no se puede dividir en tetrahedra sin introducir nuevos vértices.
Bricard octahedron, un poliedro flexible no-convexo

Más generalmente, un octaedro puede ser cualquier poliedro con ocho caras. El octaedro regular tiene 6 vértices y 12 aristas, el mínimo para un octaedro; octaedros irregulares pueden tener hasta 12 vértices y 18 aristas. Hay 257 octaedros topológicamente distintos convexos, excluyendo las imágenes especulares. Más específicamente, hay 2, 11, 42, 74, 76, 38, 14 para octaedros con 6 a 12 vértices respectivamente. (Dos poliedros son "topológicamente distintos" si tienen arreglos de caras y vértices intrínsecamente diferentes, de modo que es imposible distorsionar uno en el otro simplemente cambiando las longitudes de los bordes o los ángulos entre los bordes o las caras.)

Algunos octaedros irregulares más conocidos incluyen los siguientes:

El prisma hexagonal: Dos caras son hexágonos regulares paralelos; seis plazas vinculan pares correspondientes de bordes hexagonales.
pirámide heptagonal: Una cara es un heptógono (normalmente), y las siete caras restantes son triángulos (normalmente isosceles). No es posible que todas las caras triangulares sean equilaterales.
Truncated tetrahedron: Las cuatro caras del tetraedro están truncadas para convertirse en hexágonos regulares, y hay cuatro caras triángulo equilátero más donde cada vértice de tetraedro fue truncado.
Tetragonal trapezohedron: Las ocho caras son cometas congruentes.
Hosohedro Octagonal: degenerado en el espacio Euclideano, pero se puede realizar esféricamente.

Octaedros en el mundo físico

Octaedros en la naturaleza

Octaedro fluorita.

Los cristales naturales del diamante, el alum o el fluorito son comúnmente octaedral, como el panal tetraedral-octaedral lleno de espacio.
Las placas de aleación kamacita en meteoritos octahedritos se organizan paralelamente a las ocho caras de un octaedro.
Muchos iones metálicos coordinan seis ligandos en una configuración octaedral o distorsionada.
Patrones Widmanstätten en cristales nickel-iron

Octaedros en el arte y la cultura

Dos serpientes de Rubik de forma idéntica pueden aproximarse a un octaedro.

Especialmente en juegos de rol, este sólido se conoce como un "d8", uno de los dados poliedral más comunes.
Si cada borde de un octaedro es reemplazado por un resistor de uno-ohm, la resistencia entre vértices opuestos es 1/2 Ohm, y eso entre vértices adyacentes 5/12 Ohm.
Se pueden organizar seis notas musicales en los vértices de un octaedro de tal manera que cada borde representa un dyad consonante y cada cara representa una tríada consonante; vea hexany.

Armadura octeto tetraédrica

Buckminster Fuller inventó en la década de 1950 una estructura espacial de tetraedros y semi-octaedros alternados derivados del panal tetraédrico-octaédrico. Se considera comúnmente como la estructura de construcción más fuerte para resistir esfuerzos en voladizo.

Poliedros relacionados

Un octaedro regular se puede aumentar en un tetraedro agregando 4 tetraedros en caras alternas. Agregar tetraedros a las 8 caras crea el octaedro estrellado.

tetrahedron	octaedro estelar

El octaedro es uno de una familia de poliedros uniformes relacionados con el cubo.

Uniform octaedral polyhedra
Simetría: [4,3], (*432)							[4,3]⁺ (432)	[1]⁺,4,3] = [3,3] (*332)		[3]⁺,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{3^1.1}	t{3,4} t{3^1.1}	{3,4} {3}^1.1}	rr{4,3} s₂{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	S{3,4} s{3^1.1}

		=	=	=				= o	= o	=

Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

También es uno de los ejemplos más simples de un hipersimple, un politopo formado por ciertas intersecciones de un hipercubo con un hiperplano.

El octaedro está relacionado topológicamente como parte de una secuencia de poliedros regulares con los símbolos de Schläfli {3,n}, continuando en el plano hiperbólico.

*n32 mutación simetría de los revestimientos regulares: {3}n} v t e
Spherical				Euclid.	Hipersión compacta.		Paraco.	Hiperbólico no consumado

3.3	33	34	35	36	37	38	3 mujeres	3¹²ⁱ	3⁹ⁱ	3⁶ⁱ	3³ⁱ

Tetratetraedro

El octaedro regular también puede considerarse un tetraedro rectificado, y puede llamarse tetratetraedro. Esto se puede mostrar mediante un modelo de cara de 2 colores. Con esta coloración, el octaedro tiene simetría tetraédrica.

Compara esta secuencia de truncamiento entre un tetraedro y su dual:

Familia de polihedra de tetraedral uniforme
Simetría: [3,3], (*332)							[3,3]⁺, (332)


{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duals to uniform polyhedra

V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3

Las formas anteriores también se pueden realizar como rebanadas ortogonales a la diagonal larga de un teseracto. Si esta diagonal está orientada verticalmente con una altura de 1, entonces los primeros cinco cortes anteriores ocurren a alturas r, 3/8, 1/2, 5/ 8 y s, donde r es cualquier número en el rango 0 < r ≤ 1/4, y s es cualquier número en el rango 3/4 ≤ s < 1.

El octaedro como tetratetraedro existe en una secuencia de simetrías de poliedros cuasiregulares y mosaicos con configuraciones de vértice (3.n)², progresando de mosaicos de la esfera al plano euclidiano y al plano hiperbólico. Con simetría de notación orbifold de *n32, todas estas teselaciones son construcciones de Wythoff dentro de un dominio fundamental de simetría, con puntos generadores en la esquina del ángulo derecho del dominio.

* n32 simetrías orbifold de baldosas cuasiregulares: (3.n)²
Construcción	Spherical			Euclidean	Hiperbólico
Construcción	*332	*432	*532	*632	*732	*832...	*∞32
Quasiregular cifras
Vertex	(3.3)2	(3.4)2	(3.5)2	(3.6)2	(3.7)2	(3.8)2	(3.

Antiprisma trigonal

Como antiprisma trigonal, el octaedro está relacionado con la familia de simetría diedro hexagonal.

Uniform hexagonal dihedral spherical polyhedra
Simetría: [6,2], (*622)							[6,2]⁺, (622)	[6,2]⁺], (2*3)


{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	S{2,6}
Duals to uniforms

V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Familia de uniforme n- antiprismos pasados
v
t
e
Nombre del Antiprismo	Antiprismos digonal	(Trigonal) Antiprismos triangular	(Tetragonal) Antiprisma cuadrado	Antiprisma pentagonal	Antiprisma hexagonal	Antiprismos heptagonal	Antiprisma Octagonal	Antiprisma enneagonal	Antiprisma Decagonal	Antiprisma hendecagonal	Antiprisma dodecagonal	...	Apeirogonal antiprisma
Imagen de poliedro												...
Imagen de revestimiento esférico												Imagen de azulado plano
Config de Vertex.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...	∞.3.3.3

Bipirámide cuadrada

"Regular" derecha (simétrica) n- bipirámides pasadas:
Nombre bipyramid	Bipyramid digonal	Bipirámide triangular (Véase: J12)	Bipyramid cuadrado (Véase: O)	Bipirámide pentagonal (Véase: J13)	Bipirámide hexagonal	Bipirámide heptagonal	Bipirámide octogonal	Bipyramid enneagonal	Bipyramid Decagonal	...	Bipyramid Apeirogonal
Imagen de poliedro										...
Imagen de revestimiento esférico										Imagen de azulado plano
Config facial.	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V dieta.4.4
Coxeter diagrama										...