Número F
En óptica, el número f de un sistema óptico, como la lente de una cámara, es la relación entre la distancia focal del sistema y el diámetro de la pupila de entrada (" apertura clara"). También se conoce como relación focal, relación f o f-stop, y es muy importante en fotografía. Es un número adimensional que es una medida cuantitativa de la velocidad de la lente; aumentar el número f se conoce como detener. El número f se suele indicar con una f minúscula en forma de gancho con el formato f/N, donde N es el número f.
El número f es el recíproco de la apertura relativa (el diámetro de apertura dividido por la distancia focal).
Notación
El número f N viene dado por:
Donde f{displaystyle f} es la longitud focal, y D{displaystyle D} es el diámetro del alumno de entrada (eficaz). Es costumbre escribir f-números precedidos por "f/", que forma una expresión matemática del diámetro del alumno de entrada en términos de f{displaystyle f} y N. Por ejemplo, si la longitud focal de la lente fuera de 10 mm y su diámetro de la pupila de entrada era de 5 mm, el número f sería 2. Esto se expresaría como "f/2" en un sistema de lentes. El diámetro de la abertura sería igual a f/2{displaystyle f/2}.
La mayoría de los lentes tienen un diafragma ajustable, que cambia el tamaño del tope de apertura y, por lo tanto, el tamaño de la pupila de entrada. Esto permite al profesional variar el número f, según las necesidades. Debe apreciarse que el diámetro de la pupila de entrada no es necesariamente igual al diámetro del tope de la apertura, debido al efecto de aumento de los elementos de la lente frente a la apertura.
Ignorando las diferencias en la eficiencia de transmisión de la luz, una lente con un mayor número f proyecta imágenes más oscuras. El brillo de la imagen proyectada (luminancia) en relación con el brillo de la escena en el campo de visión del objetivo (luminancia) disminuye con el cuadrado del número f. Una lente f/4 de 100 mm de distancia focal tiene un diámetro de pupila de entrada de 25 mm. Una lente f/2 de 100 mm de distancia focal tiene un diámetro de pupila de entrada de 50 mm. Dado que el área varía con el cuadrado del diámetro de la pupila, la cantidad de luz admitida por f/2 es cuatro veces mayor que la lente f/4. Para obtener la misma exposición fotográfica, el tiempo de exposición debe reducirse por un factor de cuatro.
Una lente f/4 de longitud focal de 200 mm tiene un diámetro de pupila de entrada de 50 mm. La pupila de entrada de la lente de 200 mm tiene cuatro veces el área de la f/4 pupila de entrada de la lente y, por lo tanto, recoge cuatro veces más luz de cada objeto en el campo de visión de la lente. Pero en comparación con la lente de 100 mm, la lente de 200 mm proyecta una imagen de cada objeto el doble de alto y el doble de ancho, cubriendo cuatro veces el área, por lo que ambas lentes producen la misma iluminación en el plano focal cuando se toman imágenes de una escena de un luminancia dada.
Un T-stop es un número f ajustado para tener en cuenta la eficiencia de transmisión de la luz.
Stops, convenciones f-stop y exposición
La palabra detener a veces es confusa debido a sus múltiples significados. Una parada puede ser un objeto físico: una parte opaca de un sistema óptico que bloquea ciertos rayos. El tope de apertura es el ajuste de apertura que limita el brillo de la imagen restringiendo el tamaño de la pupila de entrada, mientras que un tope de campo es un tope destinado a cortar la luz que sería fuera del campo de visión deseado y podría causar destellos u otros problemas si no se detiene.
En la fotografía, las paradas son también una unidad utilizado para cuantificar ratios de luz o exposición, con cada parada agregada que significa un factor de dos, y cada parada restringida que significa un factor de la mitad. La unidad única también se conoce como la unidad EV (valor de exposición). En una cámara, el ajuste de abertura se ajusta tradicionalmente en pasos discretos, conocidos como f-stops. Cada unoPara" está marcado con su número f correspondiente, y representa un halving de la intensidad de la luz de la parada anterior. Esto corresponde a una disminución de los diámetros del alumno y de la abertura por un factor de 1/2{displaystyle 1/{sqrt {2}} o alrededor de 0.7071, y por lo tanto un halving de la zona del alumno.
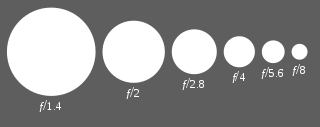
La mayoría de los lentes modernos usan una escala estándar de número f, que es una secuencia aproximadamente geométrica de números que corresponde a la secuencia de las potencias de la raíz cuadrada de 2: f/1, f/1.4, f/2, f/2.8, f/4, f/5.6, f/8, f/11, f/16, f /22, f/32, f/45, f/64, f/90, f/128, etc. Cada elemento de la secuencia es una parada por debajo del elemento a su izquierda y una parada por encima del elemento a su derecha. Los valores de las proporciones se redondean a estos números convencionales particulares, para que sean más fáciles de recordar y escribir. La secuencia anterior se obtiene aproximando la siguiente secuencia geométrica exacta:
Los fotógrafos a veces expresan otras proporciones de exposición en términos de 'paradas'. Ignorando las marcas del número f, los f-stop hacen una escala logarítmica de la intensidad de la exposición. Dada esta interpretación, se puede pensar en dar medio paso a lo largo de esta escala, para hacer una diferencia de exposición de "media parada".
Paradas fraccionarias
La mayoría de las cámaras del siglo XX tenían una apertura continuamente variable, utilizando un diafragma de iris, con cada punto marcado. La apertura de parada por clic se hizo de uso común en la década de 1960; la escala de apertura generalmente tenía una parada de clic en cada parada completa y media.
En las cámaras modernas, especialmente cuando la apertura se configura en el cuerpo de la cámara, el número f a menudo se divide más finamente que en pasos de una parada. Pasos de parada de un tercio (1⁄3 EV) son los más comunes, ya que coinciden con el sistema ISO de velocidades de película. En algunas cámaras se utilizan pasos de medio punto. Por lo general, se marcan los puntos completos y se hace clic en las posiciones intermedias. Como ejemplo, la apertura que es un tercio de parada más pequeña que f/2.8 es f/3.2, dos tercios más pequeña es f/3.5, y una parada más pequeña es f/4. Los siguientes números f en esta secuencia son:
Para calcular los pasos en un punto final (1 EV) uno podría usar
Los pasos en medio punto (1⁄2 EV) serie sería
Los pasos en una tercera parada (1⁄3 EV) serie sería
Al igual que en los estándares anteriores de velocidad de película DIN y ASA, la velocidad ISO se define solo en incrementos de un tercio de paso, y las velocidades de obturación de las cámaras digitales suelen estar en la misma escala en segundos recíprocos. Una parte del rango ISO es la secuencia
Si bien las velocidades de obturación en segundos recíprocos tienen algunas diferencias convencionales en sus números ( 1 ⁄ 15 , 1 ⁄ 30 , y 1 ⁄ 60 segundo en lugar de 1 ⁄ 16 , 1 ⁄ 32 , y 1 ⁄ 64 ).
En la práctica, la apertura máxima de una lente a menudo no es un poder integral de √ 2 (es decir, √ 2 a la potencia de un número completo), en cuyo caso generalmente es una mitad o tercera parada por encima o por debajo de una potencia integral de √ 2 .
Las lentes intercambiables controladas electrónicamente modernas, como las utilizadas para las cámaras SLR, tienen F-Stops especificados internamente en 1 ⁄ 8 -stop incrementos, por lo que las cámaras ' 1 ⁄ 3 -Spoptings se aproximan a el más cercano 1 ⁄ 8 -Stop setting in in in in in in in la lente.
Escala de número F completa estándar
incluyendo valor de apertura AV:
Números F convencionales y calculados, serie completa:
| AV | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0.5 | 0.7 | 1.0 | 1.4 | 2 | 2.8 | 4 | 5.6 | 8 | 11 | 16 | 22 | 32 | 45 | 64 | 90 | 128 | 180 | 256 |
| calculado | 0.5 | 0.707... | 1.0 | 1.414... | 2.0 | 2.828... | 4.0 | 5.657... | 8.0 | 11.31... | 16.0 | 22.62... | 32,0 | 45.25... | 64.0 | 90.51... | 128.0 | 181.02... | 256.0 |
Típica escala de número f de medio punto
| AV | −1 | −1.2 | 0 | 1.2 | 1 | 1+1.2 | 2 | 2+1.2 | 3 | 3+1.2 | 4 | 4+1.2 | 5 | 5+1.2 | 6 | 6+1.2 | 7 | 7+1.2 | 8 | 8+1.2 | 9 | 9+1.2 | 10 | 10+1.2 | 11 | 11+1.2 | 12 | 12+1.2 | 13 | 13+1.2 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0.7 | 0,8 | 1.0 | 1.2 | 1.4 | 1.7 | 2 | 2.4 | 2.8 | 3.3 | 4 | 4.8 | 5.6 | 6.7 | 8 | 9.5 | 11 | 13 | 16 | 19 | 22 | 27 | 32 | 38 | 45 | 54 | 64 | 76 | 90 | 107 | 128 |
Escala de número F típica de un tercio de la tercera parada
| AV | −1 | −2.3 | −1.3 | 0 | 1.3 | 2.3 | 1 | 1+1.3 | 1+2.3 | 2 | 2+1.3 | 2+2.3 | 3 | 3+1.3 | 3+2.3 | 4 | 4+1.3 | 4+2.3 | 5 | 5+1.3 | 5+2.3 | 6 | 6+1.3 | 6+2.3 | 7 | 7+1.3 | 7+2.3 | 8 | 8+1.3 | 8+2.3 | 9 | 9+1.3 | 9+2.3 | 10 | 10+1.3 | 10+2.3 | 11 | 11+1.3 | 11+2.3 | 12 | 12+1.3 | 12+2.3 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 0.7 | 0,8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.4 | 1.6 | 1.8 | 2 | 2.2 | 2.5 | 2.8 | 3.2 | 3.5 | 4 | 4.5 | 5.0 | 5.6 | 6.3 | 7.1 | 8 | 9 | 10 | 11 | 13 | 14 | 16 | 18 | 20 | 22 | 25 | 29 | 32 | 36 | 40 | 45 | 51 | 57 | 64 | 72 | 80 | 90 |
A veces se incluye el mismo número en varias escalas; por ejemplo, una apertura de f/1.2 se puede usar en media detener o un sistema de un tercio de parada; a veces f/1.3 y f/3.2 y otras diferencias se utilizan para la escala de parada de un tercio.
Escala típica de número f de un cuarto de parada
| AV | 0 | 1.4 | 1.2 | 3.4 | 1 | 1+1.4 | 1+1.2 | 1+3.4 | 2 | 2+1.4 | 2+1.2 | 2+3.4 | 3 | 3+1.4 | 3+1.2 | 3+3.4 | 4 | 4+1.4 | 4+1.2 | 4+3.4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1,5 | 1.7 | 1.8 | 2 | 2.2 | 2.4 | 2.6 | 2.8 | 3.1 | 3.3 | 3.7 | 4 | 4.4 | 4.8 | 5.2 | 5.6 |
| AV | 5 | 5+1.4 | 5+1.2 | 5+3.4 | 6 | 6+1.4 | 6+1.2 | 6+3.4 | 7 | 7+1.4 | 7+1.2 | 7+3.4 | 8 | 8+1.4 | 8+1.2 | 8+3.4 | 9 | 9+1.4 | 9+1.2 | 9+3.4 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 5.6 | 6.2 | 6.7 | 7.3 | 8 | 8.7 | 9.5 | 10 | 11 | 12 | 14 | 15 | 16 | 17 | 19 | 21 | 22 | 25 | 27 | 29 | 32 |
Parada H
Un H-stop (por agujero, escrito por convención con la letra H mayúscula) es un equivalente del número f para una exposición efectiva basada en el área cubierta por los agujeros en los discos de difusión o la abertura del tamiz que se encuentran en lentes Rodenstock Imagon.
T-parada
Un T-stop (para paradas de transmisión, por convención escrito con la letra T mayúscula) es un número f ajustado para tener en cuenta la eficiencia de transmisión de luz (transmitancia). Una lente con un T-stop de N proyecta una imagen del mismo brillo que una lente ideal con 100 % de transmitancia y una f -número de N. El T-stop de una lente en particular, T, se obtiene dividiendo el número f por la raíz cuadrada de la transmitancia de esa lente:
Con una pérdida del 8 % por superficie de vidrio de aire en lentes sin recubrimiento, el recubrimiento múltiple de lentes es la clave en el diseño de lentes para disminuir las pérdidas de transmisión de lentes. Algunas revisiones de lentes miden el T-stop o la tasa de transmisión en sus puntos de referencia. A veces se usan paradas en T en lugar de números f para determinar con mayor precisión la exposición, particularmente cuando se usan fotómetros externos. Las transmitancias de la lente del 60 % al 95 % son típicas. Los pasos en T se utilizan a menudo en cinematografía, donde se ven muchas imágenes en rápida sucesión e incluso se notan pequeños cambios en la exposición. Los objetivos de las cámaras de cine normalmente se calibran en pasos en T en lugar de números f. En fotografía fija, sin necesidad de una consistencia rigurosa de todas las lentes y cámaras utilizadas, las ligeras diferencias en la exposición son menos importantes; sin embargo, los T-stops todavía se usan en algunos tipos de lentes para fines especiales, como los lentes Smooth Trans Focus de Minolta y Sony.
Regla de los 16 soleados
Un ejemplo del uso de números f en fotografía es la regla de los 16 soleados: se obtendrá una exposición aproximadamente correcta en un día soleado usando una apertura de f/16 y la velocidad de obturación más cercana al recíproco de la velocidad ISO de la película; por ejemplo, con película ISO 200, una apertura de f/16 y un obturador velocidad de 1⁄200 segundo. El número f se puede ajustar hacia abajo para situaciones con poca luz. Seleccionar un número f más bajo es "abrir" la lente Seleccionar un número f más alto es "cerrar" o "detenerse" la lente
Efectos en la nitidez de la imagen
La profundidad de campo aumenta con el número f, como se ilustra en la imagen aquí. Esto significa que las fotografías tomadas con un número f bajo (apertura grande) tenderán a tener sujetos enfocados a una distancia, con el resto de la imagen (elementos más cercanos y más lejanos) desenfocados. Esto se usa con frecuencia para fotografía de naturaleza y retratos porque el desenfoque del fondo (la cualidad estética conocida como 'bokeh') puede ser estéticamente agradable y enfoca al espectador en el sujeto principal en primer plano. La profundidad de campo de una imagen producida en un número f determinado también depende de otros parámetros, incluida la distancia focal, la distancia del sujeto y el formato de la película o el sensor utilizado para capturar la imagen. La profundidad de campo se puede describir como dependiendo solo del ángulo de visión, la distancia del sujeto y el diámetro de la pupila de entrada (como en el método de von Rohr). Como resultado, los formatos más pequeños tendrán un campo más profundo que los formatos más grandes con el mismo número f para la misma distancia de enfoque y el mismo ángulo de visión, ya que un formato más pequeño requiere una distancia focal más corta (lente de ángulo más amplio) para producir el mismo ángulo. de vista, y la profundidad de campo aumenta con distancias focales más cortas. Por lo tanto, los efectos de profundidad de campo reducida requerirán números f más pequeños (y, por lo tanto, ópticas potencialmente más difíciles o complejas) cuando se usan cámaras de formato pequeño que cuando se usan cámaras de formato más grande.
Más allá del enfoque, la nitidez de la imagen está relacionada con el número f a través de dos efectos ópticos diferentes: la aberración, debido al diseño imperfecto de la lente, y la difracción, que se debe a la naturaleza ondulatoria de la luz. El f-stop de desenfoque óptimo varía según el diseño de la lente. Para las lentes estándar modernas que tienen 6 o 7 elementos, la imagen más nítida se suele obtener alrededor de f/5.6–f/8, mientras que para lentes estándar más antiguos que tienen solo 4 elementos (Fórmula Tessar) detenerse en f/11 dará la imagen más nítida. La mayor cantidad de elementos en las lentes modernas permite al diseñador compensar las aberraciones, lo que permite que la lente brinde mejores imágenes con números f más bajos. Con aperturas pequeñas, se mejoran la profundidad de campo y las aberraciones, pero la difracción genera una mayor dispersión de la luz, lo que provoca desenfoque.
La caída de luz también es sensible a f-stop. Muchas lentes gran angular mostrarán una caída de luz significativa (viñeteado) en los bordes para aperturas grandes.
Los fotoperiodistas tienen un dicho, "f/8 and be there", lo que significa que estar en la escena es más importante que preocuparse por los detalles técnicos. Prácticamente, f/8 (en formatos de 35 mm y mayores) permite una profundidad adecuada de campo y suficiente velocidad de la lente para una exposición base decente en la mayoría de las situaciones de luz diurna.
Ojo humano
Calcular el número f del ojo humano implica calcular la apertura física y la distancia focal del ojo. La pupila puede tener un tamaño de 6 a 7 mm de ancho abierto, lo que se traduce en la apertura física máxima.
El número f del ojo humano varía desde aproximadamente f/8.3 en un lugar muy iluminado a una f/2.1 en la oscuridad. El cálculo de la distancia focal requiere que se tengan en cuenta las propiedades de refracción de la luz de los líquidos en el ojo. Tratar el ojo como una cámara y un objetivo ordinarios llenos de aire da como resultado una distancia focal y un número f incorrectos.
Relación focal en telescopios
En la astronomía, el número f se conoce comúnmente como el ratio focal (o f-ratio) notated as N{displaystyle N}. Todavía se define como la longitud focal f{displaystyle f} de un objetivo dividido por su diámetro D{displaystyle D} o por el diámetro de una parada de abertura en el sistema:
Aunque los principios de la relación focal son siempre los mismos, la aplicación a la que se somete el principio puede diferir. En fotografía, la relación focal varía la iluminancia del plano focal (o potencia óptica por unidad de área en la imagen) y se utiliza para controlar variables como la profundidad de campo. Cuando se utiliza un telescopio óptico en astronomía, no hay problemas de profundidad de campo, y el brillo de las fuentes de puntos estelares en términos de potencia óptica total (no dividida por el área) es una función del área de apertura absoluta únicamente, independientemente de la distancia focal. La distancia focal controla el campo de visión del instrumento y la escala de la imagen que se presenta en el plano focal a un ocular, placa de película o CCD.
Por ejemplo, el telescopio SOAR de 4 metros tiene un campo de visión pequeño (alrededor de f /16) que es útil para estudios estelares. El telescopio LSST de 8,4 m, que cubrirá todo el cielo cada tres días, tiene un campo de visión muy amplio. Su distancia focal corta de 10,3 m (f/1.2) es posible gracias a un error sistema de corrección que incluye espejos secundarios y terciarios, un sistema de refracción de tres elementos y montaje activo y óptica.
Ecuación de cámara (G#)
La ecuación de la cámara, o G#, es la relación entre la radiación que llega al sensor de la cámara y la radiación en el plano focal de la lente de la cámara:
donde τ es el coeficiente de transmisión de la lente y las unidades están en estereorradianes inversos (sr−1 ).
Número f de trabajo
El número f describe con precisión la capacidad de captación de luz de una lente solo para objetos a una distancia infinita. Esta limitación generalmente se ignora en fotografía, donde el número f se usa a menudo independientemente de la distancia al objeto. En el diseño óptico, a menudo se necesita una alternativa para los sistemas en los que el objeto no está lejos de la lente. En estos casos se utiliza el número f de trabajo. El número f de trabajo Nw viene dado por:
Donde N es el número f no corregido, NAi es la abertura numérica del espacio-imagen de la lente, SilenciomSilencio{displaystyle Silencioso es el valor absoluto de la ampliación de la lente para un objeto a una distancia particular, y P es la ampliación de la pupila. Dado que la magnificación de la pupila raramente se sabe que a menudo se supone que es 1, que es el valor correcto para todas las lentes simétricas.
En fotografía, esto significa que a medida que uno enfoca más de cerca, la apertura efectiva de la lente se vuelve más pequeña, lo que hace que la exposición sea más oscura. El número f de trabajo a menudo se describe en fotografía como el número f corregido para las extensiones de la lente por un factor de fuelle. Esto es de particular importancia en la fotografía macro.
Historia
El sistema de números f para especificar aperturas relativas evolucionó a fines del siglo XIX, en competencia con varios otros sistemas de notación de apertura.
Orígenes de la apertura relativa
En 1867, Sutton y Dawson definieron la "relación apertal" como esencialmente el recíproco del número f moderno. En la siguiente cita, un "relación de apertura" de "1⁄24& #34; se calcula como la relación de 6 pulgadas (150 mm) a 1⁄4 pulgadas (6,4 mm), correspondiente a una f /24 f-stop:
En cada lente hay, correspondiente a una relación apertal determinada (es decir, la relación del diámetro de la parada a la longitud focal), una cierta distancia de un objeto cercano de ella, entre el cual e infinidad todos los objetos están en igual enfoque. Por ejemplo, en una sola vista de enfoque de 6 pulgadas, con un 1.4 in. stop (apertal ratio one-twenty-fourth), todos los objetos situados a distancias situadas entre 20 pies de la lente y una distancia infinita de ella (una estrella fija, por ejemplo) están en igualmente buen enfoque. Por lo tanto, se llama la gama focal del objetivo cuando se utiliza esta parada. El rango focal es por lo tanto la distancia del objeto más cercano, que estará en buen foco cuando el vidrio de tierra se ajusta para un objeto extremadamente distante. En la misma lente, la gama focal dependerá del tamaño del diafragma utilizado, mientras que en diferentes lentes con la misma relación apertal los rangos focales serán mayores a medida que se aumente la longitud focal de la lente. Los términos ' ratio apertal' y 'rango focal' no han llegado al uso general, pero es muy deseable que, con el fin de prevenir la ambigüedad y la circunlocución al tratar las propiedades de los lentes fotográficos.
En 1874, John Henry Dallmeyer llamó a la relación 1/N{displaystyle 1/N} la " ratio de intensidad" de una lente:
El rapidez de una lente depende de la relación o proporción de la abertura al enfoque equivalente. Para determinar esto, dividir el concentración equivalente por el diámetro del real abertura de trabajo de la lente en cuestión; y nota el cociente como el denominador con 1, o unidad, para el numerador. Así, para encontrar la relación de una lente de 2 pulgadas de diámetro y 6 pulgadas de enfoque, dividir el enfoque por la abertura, o 6 dividido por 2 iguales 3; es decir, 1.3 es la relación de intensidad.
Aunque aún no tenía acceso a la teoría de oclusivas y pupilas de Ernst Abbe, que Siegfried Czapski puso a disposición del público en 1893, Dallmeyer sabía que su apertura de trabajo no era la igual que el diámetro físico del tope de apertura:
Debe observarse, sin embargo, que para encontrar lo real ratio de intensidad, se debe determinar el diámetro de la abertura de trabajo real. Esto se logra fácilmente en el caso de lentes individuales, o para lentes de doble combinación utilizados con la abertura completa, estos meramente requieren la aplicación de un par de compases o regla; pero cuando se utilizan lentes de doble o triple combinación, con paradas insertadas entre las combinaciones, es algo más problemático; porque es obvio que en este caso el diámetro de la parada empleada no es la medida del lápiz real de luz transmitida por la combinación frontal. Para determinar esto, centrarse en un objeto distante, eliminar la pantalla de enfoque y reemplazarla por la diapositiva de collodion, habiendo insertado previamente un pedazo de cartón en lugar de la placa preparada. Hacer un pequeño agujero redondo en el centro del cartón con un muelle, y ahora retirar a una habitación oscura; aplicar una vela cerca del agujero, y observar el parche iluminado visible en la combinación frontal; el diámetro de este círculo, cuidadosamente medido, es la abertura de trabajo real de la lente en cuestión para la parada particular empleada.
Este punto es enfatizado aún más por Czapski en 1893. Según una revisión en inglés de su libro, en 1894, "Se insiste fuertemente en la necesidad de distinguir claramente entre la apertura efectiva y el diámetro del tope físico".;
J. El hijo de H. Dallmeyer, Thomas Rudolphus Dallmeyer, inventor del teleobjetivo, siguió la terminología de índice de intensidad en 1899.
Sistemas de numeración de apertura
Al mismo tiempo, hubo una serie de sistemas de numeración de apertura diseñados con el objetivo de hacer que los tiempos de exposición varíen en proporción directa o inversa con la apertura, en lugar de con el cuadrado del número f o el inverso del cuadrado de la apertura. relación o relación de intensidad. Pero todos estos sistemas involucraban alguna constante arbitraria, en oposición a la simple proporción de distancia focal y diámetro.
Por ejemplo, el Sistema Uniforme (EE. UU.) de aperturas fue adoptado como estándar por la Photographic Society of Great Britain en la década de 1880. Bothamley en 1891 dijo: "Las paradas de todos los mejores fabricantes ahora se organizan de acuerdo con este sistema". U.S. 16 tiene la misma apertura que f/16, pero las aperturas son más grandes o más pequeño por un punto use la duplicación o la reducción a la mitad del número de EE. UU., por ejemplo f /11 es U.S. 8 y f/8 es U.S. 4. El tiempo de exposición requerido es directamente proporcional al número de EE.UU. Eastman Kodak usó paradas estadounidenses en muchas de sus cámaras al menos en la década de 1920.
Para 1895, Hodges contradice a Bothamley, diciendo que el sistema de números f se ha hecho cargo: "Esto se llama f/x, y los diafragmas de todos los lentes modernos de buena construcción están tan marcados."
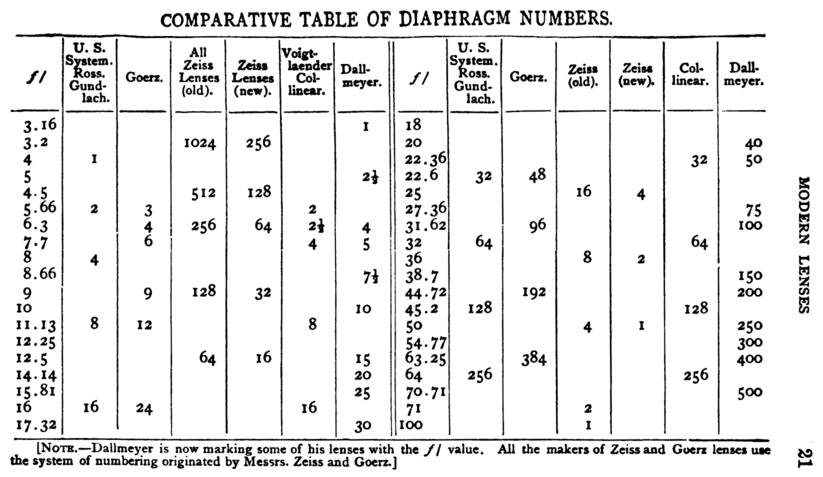
Esta es la situación vista en 1899:
Piper en 1901 analiza cinco sistemas diferentes de marcado de apertura: los sistemas Zeiss antiguo y nuevo basados en la intensidad real (proporcional al cuadrado recíproco del número f); y los sistemas de EE. UU., C.I. y Dallmeyer basados en la exposición (proporcional al cuadrado del número f). Él llama al número f el "número de razón" "número de relación de apertura," y "relación de apertura." Él llama a expresiones como f/8 el "diámetro fraccional" de la apertura, aunque es literalmente igual al "diámetro absoluto" que él distingue como un término diferente. A veces también usa expresiones como "una apertura de f 8" sin la división indicada por la barra oblicua.
Beck y Andrews en 1902 hablan sobre el estándar de f de la Royal Photographic Society /4, f/5.6, f/8, f/11.3, etc. El R.P.S. habían cambiado su nombre y se habían salido del sistema de EE. UU. en algún momento entre 1895 y 1902.
Estandarización tipográfica
En 1920, el término f-number apareció en libros como F number y f/number. En las publicaciones modernas, las formas f-number y f number son más comunes, aunque las formas anteriores, así como el F-number todavía son encontrado en algunos libros; no es raro que la minúscula inicial f en f-number o f/number se establezca en cursiva enganchada: ƒ.
Las notaciones para los números f también fueron bastante variables a principios del siglo XX. A veces se escribían con una F mayúscula, a veces con un punto (punto) en lugar de una barra oblicua y, a veces, se establecían como una fracción vertical.
La norma ASA de 1961 PH2.12-1961 Medidores de exposición fotográfica estándar estadounidense de propósito general (tipo fotoeléctrico) especifica que "El símbolo para las aperturas relativas debe ser ƒ/ o ƒ: seguido por el número ƒ efectivo." Muestran la cursiva enganchada 'ƒ' no solo en el símbolo, sino también en el término f-number, que hoy en día se encuentra más comúnmente en una cara normal sin cursiva.
Contenido relacionado
USB (desambiguación)
PCHP
Instituto de Estudios Avanzados de Corea