Número de Stirling

En matemáticas, los números de Stirling surgen en una variedad de problemas analíticos y combinatorios. Reciben su nombre de James Stirling, quien los introdujo en un entorno puramente algebraico en su libro Methodus differenceis (1730). Masanobu Saka los redescubrió y les dio un significado combinatorio en 1782.

Dos conjuntos diferentes de números llevan este nombre: los números de Stirling del primer tipo y los números de Stirling del segundo tipo. Además, los números de Lah a veces se denominan números de Stirling de tercer tipo. Cada especie se detalla en su respectivo artículo, sirviendo éste de descripción de las relaciones entre ellas.

Una propiedad común de los tres tipos es que describen coeficientes que relacionan tres secuencias diferentes de polinomios que surgen con frecuencia en la combinatoria. Además, los tres pueden definirse como el número de particiones de n elementos en k subconjuntos no vacíos, con diferentes formas de contar los ordenamientos dentro de cada subconjunto.

Notación

Se utilizan varias notaciones diferentes para los números de Stirling. La notación común para los números de Stirling de primera clase ordinarios (con signo) es:

${displaystyle s(n,k),}$

Para números de Stirling sin signo del primer tipo, que cuentan el número de permutaciones de n elementos con k ciclos disjuntos, es:

${biggl {biggl {natop k}{biggr}=c(n,k)= bendiciones(n,k)$

Y para los números de Stirling del segundo tipo, que cuentan el número de formas de dividir un conjunto de n elementos en k subconjuntos no vacíos:

${displaystyle {biggl}{!n! {cHFF}=S(n,k)=S_{n} {(k)},}$

Por ejemplo, la suma ${textstyle displaystyle sum _{k=0}n}left[{n atop k}right]=n!}$ es el número de todas las permutaciones, mientras que la suma ${textstyle displaystyle sum _{k=0}n}left{\!n! ¡Detente!$ es nEl número de Bell.

Abramowitz y Stegun usan una maleta superior ${displaystyle S.$ y un blackletter ${displaystyle {\\sh00}$, respectivamente, para el primer y segundo tipo de número de Stirling. La notación de corchetes y aparatos, en analogía con los coeficientes binomiales, fue introducida en 1935 por Jovan Karamata y promovida posteriormente por Donald Knuth. (La notación entre corchetes conflictos con una notación común para los coeficientes gausianos.) La motivación matemática para este tipo de notación, así como fórmulas adicionales de número de Stirling, se puede encontrar en la página para números de Stirling y funciones de generación exponencial.

Expansiones de factoriales ascendentes y descendentes

Los números de Stirling expresan coeficientes en expansiones de factoriales descendentes y ascendentes (también conocido como el símbolo de Pochhammer) como polinomios.

Es decir, el caída factorial, definido como ${displaystyle (x)_{n}=x(x-1)cdots (x-n+1)}$, es un polinomio en x grado n cuya expansión

${displaystyle (x)_{n}=sum _{k=0}s(n,k)x^{k}$

con números de Stirling (con signo) de primera clase como coeficientes.

Note that (x)₀ = 1 porque es un producto vacío. Los combinatorialistas también a veces usan la notación ${displaystyle x^{compline {n}}$ por la caída factorial, y ${displaystyle x^{soverline {n}}$ para el factorial creciente. (Confuso, el símbolo Pochhammer que muchos usan para caída factoriales se utiliza en funciones especiales para en aumento factoriales.)

Del mismo modo, el creciente factorial, definido como ${displaystyle x^{(n)}=x(x+1)cdots (x+n-1)}$, es un polinomio en x grado n cuya expansión

${displaystyle x^{(n)}=sum _{k=0}{n}{biggl [}{n atop k} {biggr}x^{k}=sum _{k=0}{n}(-1)^{n-k}s(n,k)x^{k}$

con números de Stirling de primer tipo como coeficientes. Una de estas expansiones puede derivarse de la otra observando que ${displaystyle x^{(n)}=(-1)^{n}(-x)_{n}$.

Los números de Stirling del segundo tipo expresan las relaciones inversas:

${displaystyle x^{n}=sum _{k=0}{n}S(n,k)(x)_{k}$

y

${displaystyle x^{n}=sum _{k=0}{n}(-1)^{n-k}S(n,k)x^{(k)}$

Como cambio de coeficientes de base

Considerando el conjunto de polinomios en la variable (indeterminada) x como un espacio vectorial, cada una de las tres secuencias

${displaystyle x^{0},x^{1},x^{2},x^{3},dots quad (x)_{0},(x)_{1},(x)_{2},dots quad x^{(0)},x^{(1)},x^{(2)},dots }$

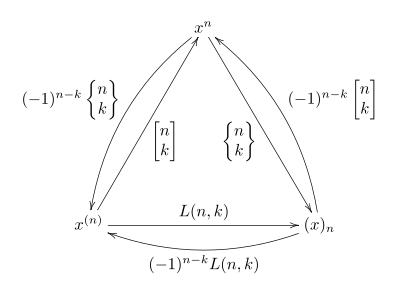
es una base. Es decir, cada polinomio en x puede ser escrito como una suma ${displaystyle a_{0}x^{(0)}+a_{1}x^{(1)}+dots +a_{n}x^{(n)}}$ para algunos coeficientes únicos ${displaystyle A_{i}$ (similarmente para las otras dos bases). Las relaciones anteriores expresan entonces el cambio de base entre ellas, como se resume en el siguiente diagrama conmutativo:

Los coeficientes para los dos cambios de fondo se describen en los números Lah a continuación. Puesto que los coeficientes en cualquier base son únicos, se puede definir números de Stirling de esta manera, como los coeficientes que expresan polinomios de una base en términos de otra, es decir, los números únicos relacionados ${displaystyle x^{n}$ con la caída y el aumento de los factores como arriba.

Los factores de caída definen, hasta escalar, los mismos polinomios como coeficientes binomiales: ${fnMicrosoft} {x}=(x)_{k}/k!}$. Los cambios entre la base estándar ${displaystyle textstyle x^{0},x^{1},x^{2},dots }$ y la base ${benom {binom} {binom}} {binom {x}}} {binom {binom {x}{2}}},dots }$ son descritos por fórmulas similares:

${displaystyle x^{n}=sum _{k=0}{n}{biggl{\\!n! atop !k! {biggr ¡Ky! {x} {k}quad {text{and}}quad {binom {x} {fn}}==sum ¡No!$.

Como matrices inversas

Los números de Stirling del primer y segundo tipo pueden considerarse inversos entre sí:

${displaystyle sum _{jgeq 0}s(n,j)S(j,k)=sum _{jgeq 0}(-1)^{n-j}{biggl [}{natop j}{biggr]}{biggl {}{!j! atop !k! {biggr}=delta ¿Qué?$

y

${displaystyle sum _{jgeq 0}S(n,j)s(j,k)=sum _{jgeq 0}(-1)^{j-k}{biggl {{\!n! {biggl [}{j atop k}{biggr]}=delta ¿Qué?$

Donde ${displaystyle delta _{nk}$ es el Kronecker delta. Estas dos relaciones pueden entenderse como relaciones inversas de matriz. Eso es, vamos s ser la matriz triangular inferior de los números del primer tipo, cuyos elementos de matriz ${displaystyle s_{nk}=s(n,k)}$El inverso de esta matriz es S, la matriz triangular inferior de números de Stirling del segundo tipo, cuyas entradas son ${displaystyle S_{nk}=S(n,k). }$ Simbólicamente, esto está escrito

${displaystyle s^{-1}=S,}$

Aunque s y S son infinitas, por lo que calcular una entrada de producto implica una suma infinita, las multiplicaciones de matrices funcionan porque estas matrices son triangulares inferiores, por lo que solo un número finito de los términos de la suma son distintos de cero.

Ejemplo

Expresar un polinomio en base a factoriales descendentes es útil para calcular sumas del polinomio evaluado en números enteros consecutivos. De hecho, la suma de un factorial descendente se expresa simplemente como otro factorial descendente (para k≠−1)

${displaystyle sum _{0leq i)_{k}={frac {(n)_{k+1}{k+1}}} {k+1}}}} {c}} {c}}}} {cccc}}}} {cc}}}$

Esto es análogo a la integral ${textstyle int ¿Por qué?$, aunque la suma debe ser sobre enteros i estrictamente inferior a n.

Por ejemplo, la suma de cuartas potencias de números enteros hasta n (esta vez con n incluido), es:

${displaystyle {begin{aligned} ¿Qué? ¿Qué? ¿Qué? {fnMicrosoft Sans Serif} atop !k! {biggr}(i)_{k}=sum ¡No! {n+1)_{k+1}[8mu] ={biggl {fnMicrosoft Sans Serif} {n+1)_{2}}+{biggl}}{biggl}}{biggl}}{biggl {fnMicrosoft Sans Serif} atop !2! {biggr}{frac {(n+1)_{3}{3}}+{biggl {fnMicrosoft Sans Serif} {n+1)}{4}}+{biggl}}{biggl}}{biggl {fnMicrosoft Sans Serif} atop !4!}{biggr}{frac {(n+1)_{5}{5}[8mu] limitquad ={2} {2}(n+1)_{2}+{frac}+{frac {7}{3}(n+1)_{3}+{frac {6}{4}(n+1)_{4}+{frac {1}{5} {5} {5}} {5} {fn}}} {fn}} {fn}} {fn}}} {fn}}} {fn}}}}}} {fn}}}}}}} {fn}}} {n}}}} {fn}}}}}}}}}}}}}}}}}}}}}} {n}}}}} {n}}}}}}}}}}}}}}}}}}}}}} {n}}} {n}}}}}}}}}}}}}}}}}}}}}}}}}} {n}}}}} {n}}}}}}}}}}}}}}}}}}}}}} {n}}}}}}}}} {n}}}}}}}}}}}}}}}}}}}}}}}}}}}} {$

Aquí, los números de Stirling se pueden calcular a partir de su definición como el número de particiones de 4 elementos en k subconjuntos no vacíos sin etiquetar.

En cambio, la suma ${textstyle sum ¿Qué?$ en la base estándar es dada por la fórmula de Faulhaber, que en general es más compleja.

Números lah

Los números de Lah ${displaystyle L(n,k)={n-1 choose k-1}{frac !$ a veces se llaman números del tercer tipo. Por convención, ${displaystyle L(0,0)=1}$ y ${displaystyle L(n,k)=0}$ si ${displaystyle n títulok}$ o ${displaystyle k=0cantado}$.

Estos números son coeficientes que expresan factoriales descendentes en términos de factoriales ascendentes y viceversa:

${displaystyle x^{(n)}=sum _{k=0}{n}L(n,k)(x)_{k}quad }$ y ${displaystyle quad (x)_{n}=sum _{k=0}{n}(-1)^{n-k}L(n,k)x^{(k)}$

Como antecedente, esto significa que expresan el cambio de base entre las bases ${displaystyle (x)_{0},(x)_{1},(x)_{2},cdots }$ y ${displaystyle x^{(0)},x^{(1)},x^{(2)},cdots }$, completar el diagrama. En particular, una fórmula es el inverso del otro, por lo tanto:

${displaystyle sum _{j}L(n,j)cdot (-1)^{j-k}L(j,k)=delta - Sí.$

Análogamente, componiendo, por ejemplo, el cambio de base de ${displaystyle x^{(n)}}$ a ${displaystyle x^{n}$ con el cambio de base de ${displaystyle x^{n}$ a ${displaystyle (x)_{n}$ da el cambio de base directamente desde ${displaystyle x^{(n)}}$ a ${displaystyle (x)_{n}$:

${displaystyle L(n,k)=sum _{j}{biggl [}{natop j}{biggr]}{biggl {}{!j! ¡Detente!$

En términos de matrices, si ${displaystyle L.$ denota la matriz con entradas ${displaystyle L_{nk}=L(n,k)}$ y ${displaystyle L^{-}$ denota la matriz con entradas ${displaystyle ¿Qué?$, entonces uno es el inverso del otro: ${displaystyle L^{-}=L^{-1}$. Del mismo modo, la composición de la matriz de números de Stirling insigned del primer tipo con la matriz de números de Stirling del segundo tipo da los números de Lah: ${displaystyle L= imperfecciones subsistencdot S.$.

Los números ${textstyle left{!n! atop !k!right},left[{n atop k}right],L(n,k)}$ se puede definir como el número de particiones de n elementos k subconjuntos no vacíos sin etiquetar, cada uno de los cuales es desordenado, ordenado cíclicamente o ordenado linealmente, respectivamente. En particular, ello implica las siguientes desigualdades:

${displaystyle {biggl}{!n! atop !k! {biggr}leq {biggl [}{n atop k}{biggr ]}leq L(n,k). }$

Fórmulas simétricas

Abramowitz y Stegun dan las siguientes fórmulas simétricas que relacionan los números de Stirling de primera y segunda especie.

${displaystyle s(n,k)=sum _{j=0}{n-k}{j}{n-1+j} choose n-k+j}{2n-k choose n-k-j}S(n-k+j,j)}$

y

${displaystyle S(n,k)=sum _{j=0}{n-k}(-1)^{j}{n-1+j} choose n-k+j}{2n-k choose n-k-j}s(n-k+j,j). }$

Números de Stirling con valores enteros negativos

Los números de Stirling se pueden extender a valores enteros negativos, pero no todos los autores lo hacen de la misma manera. Independientemente del enfoque adoptado, vale la pena señalar que los números de Stirling de primera y segunda clase están conectados por las relaciones:

${biggl} {biggl}={biggl}={biggl ¡Ah, sí! atop !-n! {biggr}quad {text{and}quad {biggl {}{!n! atop !k! {biggr {biggl} [}{-k atop -n} {biggr ]}$

cuando n y k son enteros no negativos. Así que tenemos la siguiente tabla para ${displaystyle left[{-n atop -k}right]$:

Donald Knuth definió los números de Stirling más generales al extender una relación de recurrencia a todos los enteros. En este enfoque, ${textstyle left[{n atop k}right]$ y ${textstyle left{!n! ¡Detente!$ son cero si n es negativo k es no negativo, o si n no negativo k es negativo, y así lo tenemos, cualquiera enteros n y k,

${biggl} {biggl}={biggl}={biggl ¡Ah, sí! atop !-n! {biggr}quad {text{and}quad {biggl {}{!n! atop !k! {biggr {biggl} [} {-k atop -n} {biggr ]}$

Por otro lado, para números enteros positivos n y k, David Branson definido ${textstyle left[{-n atop -k}right]!, }$ ${textstyle left{!-n! atop ! }$ ${textstyle left[{-n atop k}right]!,}$ y ${textstyle left{!-n! ¡Detente!$ (pero no ${textstyle left[{n atop -k}right]$ o ${textstyle left{!n! ¡Detente!$). En este enfoque, uno tiene la siguiente extensión de la relación de recurrencia del número de Stirling del primer tipo:

${biggl {biggl}{biggr}={frac {=-1)^{n+1} {}}}sum}}} ¿Por qué? {n}{i}}$,

Por ejemplo, ${textstyle left[{-5 atop k}right]={frac {1}{120}{Bigl (}5-{frac {10}{2^{k}}}+{frac}}{frac} {f}} {f} {fnK} {fnMicroc} {5}{4}} {fn} {fnK}} {f}} {f}} {f}} {fn}}}} {fn} {fn}}} {fn}}}} {fn}}}}}}}} {f}} {f}}} {f}}}}}}}}}}}}}}}}}}} {\\\\\f}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}} {\\\\\\\\f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} Más grande.$ Esto lleva a la siguiente tabla de valores ${textstyle left[{-n atop k}right]$.

k n	0	1	2	3	4
−1	1	1	1	1	1
−2	${fnMicroc} {-1}{2}}$	${fnMicroc} {-3}{4}}$	${fnMicroc} {-7}{8}}$	${displaystyle {tfrac {-15}{16}}$	${fnMicroc} {-31}{32}}$
−3	${fnMicroc} {1}{6}}$	${displaystyle {tfrac}{36}}}$	${displaystyle {tfrac {85}{216}}$	${displaystyle {tfrac {575}{1296}}$	${displaystyle {tfrac {3661}{7776}}$
−4	${fnMicroc} {-1}{24}}$	${displaystyle {tfrac {-25}{288}}$	${displaystyle {tfrac {-415}{3456}}$	${displaystyle {tfrac {-5845}{41472}}$	${displaystyle {tfrac {-76111}{497664}}$
; 5 -	${displaystyle {tfrac {1}{120}}$	${displaystyle {tfrac {137}{7200}$	${displaystyle {tfrac {12019}{432000}$	${displaystyle {tfrac {874853}{25920000}}$	${displaystyle {tfrac {58067611}{1555200000}}$

En este caso ${textstyle sum _{n=-1}{-infty }left[{-n atop -k}right]=B_{k}$ Donde ${displaystyle B_{k}$ es un número de Bell, y por lo tanto uno puede definir el negativo Números de campana ${textstyle sum _{n=-1}{-infty }left[{-n atop k}right]=B_{-k}$. Por ejemplo, esto produce ${textstyle sum _{n=-1}{-infty }left[{-n atop 2}right] =B_{-2}=0.421773ldots$.