Numero de abate

En óptica y diseño de lentes, el número de Abbe, también conocido como número V o constricción de un material transparente, es un medida aproximada de la dispersión del material (cambio del índice de refracción frente a la longitud de onda), con valores altos de V que indican baja dispersión. Lleva el nombre de Ernst Abbe (1840-1905), el físico alemán que lo definió. El término número V no debe confundirse con la frecuencia normalizada en las fibras.

Variación de índice refractivo para vidrio de peinado SF11, copa corona de borosilicate BK7 y cuarzo fundido, y cálculo para dos números de abadía para SF11.

El número de Abbe, V_d, de un material se define como

VD=nd− − 1nF− − nC,{displaystyle V_{D}={frac {n_{d} {n_{n_{F}-n_{C}}}

donde n_C, n_d y n_F son los índices de refracción del material en las longitudes de onda de las líneas espectrales de Fraunhofer C, d y F (656,3 nm, 587,56 nm y 486,1 nm respectivamente). Esta formulación solo se aplica al espectro visible. Fuera de este rango se requiere el uso de diferentes líneas espectrales. Para líneas espectrales no visibles, el término número V se usa más comúnmente. La formulación más general definida como,

V=ncentro− − 1ncorto− − nlargo,{displaystyle V={frac {n_{text{center}}} {n_{text{short}-n_{text{long}}}}}}}}}}

donde n_corto, n_centro y n_largo son los índices de refracción del material en tres longitudes de onda diferentes. El índice de longitud de onda más corto es n_corto y el más largo es n_largo.

Los números de Abbe se utilizan para clasificar el vidrio y otros materiales ópticos en función de su cromaticidad. Por ejemplo, los vidrios de pedernal de mayor dispersión tienen V < 55 mientras que los vidrios de corona de menor dispersión tienen números de Abbe más grandes. Los valores de V van desde menos de 25 para vidrios de sílex muy densos, alrededor de 34 para plásticos de policarbonato, hasta 65 para vidrios de corona comunes y de 75 a 85 para algunos vidrios de corona de fluorita y fosfato.

La mayoría de la curva de sensibilidad de longitud de onda del ojo humano, mostrada aquí, está entre corcheteada por las longitudes de onda de referencia número Abbe de 486.1 nm (azul) y 656.3 nm (rojo)

Los números de Abbe se utilizan en el diseño de lentes acromáticas, ya que su recíproco es proporcional a la dispersión (pendiente del índice de refracción frente a la longitud de onda) en la región de la longitud de onda donde el ojo humano es más sensible (consulte el gráfico). Para diferentes regiones de longitud de onda, o para una mayor precisión en la caracterización de la cromaticidad de un sistema (como en el diseño de apocromáticos), se utiliza la relación de dispersión completa (índice de refracción en función de la longitud de onda).

Diagrama de Abbe

Un diagrama de la Abadía, también conocido como "el velo de vidrio", traza el número de la Abadía contra el índice refractivo para una gama de vasos diferentes (puntos rojos). Los vidrios se clasifican usando el código número de letra Schott Glass para reflejar su composición y posición en el diagrama.

Influencias de adiciones de componentes de vidrio seleccionados en el número de abadía de un vaso base específico.

Un diagrama de Abbe, también llamado 'el velo de vidrio', se produce trazando el número de Abbe V_d de un material frente a su índice de refracción n_d. Los vasos se pueden categorizar y seleccionar de acuerdo con sus posiciones en el diagrama. Puede ser un código de letras y números, como se usa en el catálogo de Schott Glass, o un código de vidrio de 6 dígitos.

Gafas' Los números de Abbe, junto con sus índices de refracción medios, se utilizan en el cálculo de las potencias de refracción requeridas de los elementos de las lentes acromáticas para cancelar la aberración cromática de primer orden. Tenga en cuenta que estos dos parámetros que entran en las ecuaciones para el diseño de dobletes acromáticos son exactamente lo que se representa en un diagrama de Abbe.

Debido a la dificultad y la inconveniencia de producir líneas de sodio e hidrógeno, a menudo se sustituyen por definiciones alternativas del número de Abbe (ISO 7944). En lugar de la definición estándar anterior, usando la variación del índice de refracción entre las líneas de hidrógeno F y C, una medida alternativa usando el subíndice "e"

Ve=ne− − 1nF.− − nC.{displaystyle V_{e}={frac {n_{e} {n_{F}-n_{C}}

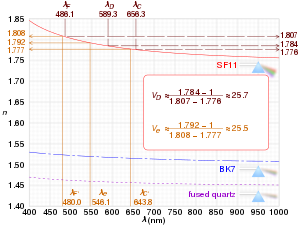
toma la diferencia entre los índices de refracción de las líneas de cadmio azul y roja a 480,0 nm y 643,8 nm (donde n_e se refiere a la longitud de onda del mercurio e- línea, 546.073 nm). Se pueden emplear otras definiciones de manera similar; la siguiente tabla enumera las longitudes de onda estándar en las que n se determina comúnmente, incluidos los subíndices estándar empleados.

Derivación

A partir de la ecuación de Lensmaker para una lente delgada

P=1f=()n− − 1)[1R1− − 1R2+()n− − 1)dnR1R2].. ()n− − 1)()1R1− − 1R2){displaystyle P={frac {1}{f}=(n-1)left[{frac] {1} {fn} {fnMicroc} {1}{2}}}}+{frac {n-1)d}{nR_{2}}}right]approx (n-1)left({frac {1} {fn} {fnMicroc} {1} {R_{2}}derecha)}

El cambio de poder refractivo P entre las dos longitudes de onda λ_corta y λ_larga viene dado por

δ δ P=Pcorto− − Plargo=()ns− − nl)()1R1− − 1R2){displaystyle delta P=P_{text{short}-P_{text{long}=(n_{s}-n_{l})left({frac {1} {fn} {fnMicroc} {1} {R_{2}}derecha)}

Esto se expresa en términos de poder P_c a λ_centro multiplicando y dividiendo por nc− − 1{displaystyle No.

δ δ P=ns− − nlnc− − 1()nc− − 1)()1R1− − 1R2)=ns− − nlnc− − 1Pc=PcV{displaystyle delta P={frac {n_{s}-n_{l} {n_{c}}(n_{c}-1)left({frac} {1} {fn} {fnMicroc} {1}{2}}derecha)={frac {n_{s}-n_{l} {n_{c}={c}={frac} {c} {c}}} {c}}} {c}}}} {c}}}} {c}}}}}} {c}}}}}} {c}}}}}} {c}}}} {c}}}}} {c}}}}}}} {c}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

El cambio relativo es inversamente proporcional a V

δ δ PPc=1V{displaystyle {frac {delta ¿Qué? {1}{V}}