Número cuántico magnético

En física atómica, un número cuántico magnético es un número cuántico utilizado para distinguir los estados cuánticos de un electrón u otra partícula según su momento angular a lo largo de un eje determinado en el espacio. El número cuántico magnético orbital (m_l o m) distingue los orbitales disponibles dentro de una subcapa determinada de un átomo. Especifica el componente del momento angular orbital que se encuentra a lo largo de un eje dado, convencionalmente llamado eje z, por lo que describe la orientación del orbital en el espacio. El número cuántico magnético de espín m_s especifica la z Componente del eje del momento angular de espín de una partícula que tiene un número cuántico de espín s. Para un electrón, s es 1⁄2 y m_{s< /sub>} es +1⁄2 o −1⁄2, a menudo llamado "spin-up" y "spin-down", o α y β. El término magnético en el nombre se refiere al momento dipolar magnético asociado con cada tipo de momento angular, por lo que los estados que tienen diferentes números cuánticos magnéticos cambian de energía en un campo magnético según el efecto Zeeman.

Los cuatro números cuánticos utilizados convencionalmente para describir el estado cuántico de un electrón en un átomo son el número cuántico principal n, el número cuántico azimutal (orbital) ${displaystyle ell }$, y los números cuánticos magnéticos m_l y m_s. Los electrones en una subshell dada de un átomo (como s, p, d, o f) se definen por valores de ${displaystyle ell }$ (0, 1, 2, o 3). El número de cuántico magnético orbital toma valores enteros en el rango desde ${displaystyle -ell }$ a ${displaystyle #$, incluyendo cero. Así las s, p, d, y f subshells contienen 1, 3, 5 y 7 órbitas cada una, con valores de m_l dentro de los rangos 0, ±1, ±2, ±3 respectivamente. Cada uno de estos orbitales puede acomodar hasta dos electrones (con giros opuestos), formando la base de la tabla periódica.

Otros números cuánticos magnéticos están definidos de manera similar, como m _j para Z --Axis componente El momento angular electrónico total j , y m _i para el spin nuclear i . Los números cuánticos magnéticos se capitalizan para indicar totales para un sistema de partículas, como m _l o < span class = "texhtml mvar" style = "font-style: italic;"> m _l para el momento total z -axis orbital angular de todo el Electrones en un átomo.

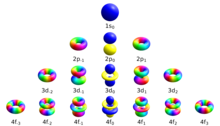
Hay un conjunto de números cuánticos asociados con los estados energéticos del átomo. Los cuatro números cuánticos ${displaystyle n}$, ${displaystyle ell }$, ${displaystyle m_{l}$, y ${displaystyle m_{s}$ especifique el estado cuántico completo de un solo electrón en un átomo llamado su funcionamiento de onda o orbital. La ecuación Schrödinger para la función de onda de un átomo con un electrón es una ecuación diferencial parcial separable. (Este no es el caso del átomo de helio neutro u otros átomos con electrones que interactúan mutuamente, que requieren métodos más sofisticados para la solución) Esto significa que la función de onda expresada en coordenadas esféricas se puede dividir en el producto de tres funciones del ángulo del radio, colatitud (o polar) y azimut:

${displaystyle psi (r,thetaphi)=R(r)P(theta)F(phi)}$

La ecuación diferencial para ${displaystyle F}$ se puede resolver en la forma ${displaystyle F(phi)=Ae^{lambda phi }$. Debido a los valores del ángulo del azimut ${displaystyle phi }$ diferenciado por 2${displaystyle pi}$ radios (360 grados) representan la misma posición en el espacio, y la magnitud general de ${displaystyle F}$ no crece con arbitrariamente grande ${displaystyle phi }$ como sería para un verdadero exponente, el coeficiente ${displaystyle lambda }$ debe ser cuantificado para múltiples enteros de ${displaystyle i}$, produciendo un exponente imaginario: ${displaystyle lambda =im_{l}$. Estos números enteros son los números cuánticos magnéticos. La misma constante aparece en la ecuación de colatitudes, donde valores más grandes ${displaystyle {m_{l}} {2}}$ tienden a disminuir la magnitud de ${displaystyle P(theta),}$ y valores de ${displaystyle m_{l}$ mayor que el número de cuántico azimutal ${displaystyle ell }$ no permite ninguna solución ${displaystyle P(theta). }$

Relación entre los números cuánticos
Orbital	Valores	Número de valores para ${displaystyle m_{l}$	Electrones por subshell
s	${displaystyle ell =0,quad m_{l}=0}$	1	2
p	${displaystyle ell =1,quad m_{l}=-1,0,+1}$	3	6
d	${displaystyle ell =2,quad m_{l}=-2,-1,0,+1,+2}$	5	10
f	${displaystyle ell =3,quad m_{l}=-3,-2,-1,0,+1,+2,+3}$	7	14
g	${displaystyle ell =4,quad m_{l}=-4,-3,-2,-1,0,+1,+2,+3,+4}$	9	18

Como componente del momento angular

El eje utilizado para las coordenadas polares en este análisis es elegido arbitrariamente. El número cuántico ${displaystyle m_{l}$ se refiere a la proyección del impulso angular en esta dirección arbitrariamente escogida, llamada convencionalmente ${displaystyle z}$- eje de dirección o cuantización. ${displaystyle L_{z}$, la magnitud del impulso angular en la ${displaystyle z}$- la dirección, es dada por la fórmula:

${displaystyle L_{z}=m_{l}hbar }$.

Este es un componente del impulso angular orbital total del electrón atómico ${displaystyle mathbf {L}$, cuya magnitud está relacionada con el número cuántico azimutal de su subshell ${displaystyle ell }$ por la ecuación:

${displaystyle L=hbar {sqrt {ell (ell +1)}}$,

Donde ${displaystyle hbar }$ es la constante de Planck reducido. Note que esto ${displaystyle L=0}$ para ${displaystyle ell =0}$ y aproximaciones ${displaystyle L=left(ell +{tfrac {1}right)hbar }$ para alto ${displaystyle ell }$. No es posible medir el impulso angular del electrón a lo largo de los tres ejes simultáneamente. Estas propiedades fueron demostradas por primera vez en el experimento Stern-Gerlach, por Otto Stern y Walther Gerlach.

Efecto en campos magnéticos

El número cuántico ${displaystyle m_{l}$ se refiere, sueltamente, a la dirección del vector de impulso angular. Número de cuántico magnético ${displaystyle m_{l}$ sólo afecta la energía del electrón si está en un campo magnético porque en ausencia de uno, todos los armónicos esféricos correspondientes a los diferentes valores arbitrarios ${displaystyle m_{l}$ son equivalentes. El número cuántico magnético determina el cambio de energía de un orbital atómico debido a un campo magnético externo (el efecto Zeeman) - por lo tanto el nombre magnética número cuántico. Sin embargo, el momento real de dipolo magnético de un electrón en una órbita atómica surge no sólo del impulso angular del electrón, sino también del giro del electrón, expresado en el número cuántico de la columna.

Puesto que cada electron tiene un momento magnético en un campo magnético, estará sujeto a un par que tiende a hacer el vector ${displaystyle mathbf {L}$ paralelo al campo, fenómeno conocido como Precesión Larmor.