Multiplicador de Lagrange

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Método para resolver problemas de optimización limitados

En optimización matemática, el método de los multiplicadores de Lagrange es una estrategia para encontrar los máximos y mínimos locales de una función sujeta a restricciones de igualdad (es decir, sujeta a la condición de que una o más ecuaciones deben cumplirse exactamente por los valores elegidos de las variables). Lleva el nombre del matemático Joseph-Louis Lagrange. La idea básica es convertir un problema restringido en una forma tal que aún se pueda aplicar la prueba derivada de un problema no restringido. La relación entre el gradiente de la función y los gradientes de las restricciones conduce de manera bastante natural a una reformulación del problema original, conocida como función lagrangiana.

El método puede resumirse como sigue: Para encontrar el máximo o mínimo de una función ${displaystyle f(x) }$ sujetos a la limitación de la igualdad ${displaystyle g(x)=0}$ forma la función Lagrangian,

{displaystyle {mathcal {L}}(x,lambda)equiv f(x)+lambda cdot g(x)}

y encontrar los puntos estacionarios de ${displaystyle {mathcal {L}} }$ considerada como una función ${displaystyle x }$ y el multiplicador Lagrange ${displaystyle lambda ~.}$ Esto significa que todos los derivados parciales deben ser cero, incluyendo el derivado parcial con respecto a ${displaystyle lambda ~.}$

{displaystyle {frac { partial {mathcal {L}} }{partial x}}=0qquad }

{displaystyle qquad {frac { partial {mathcal {L}} }{partial lambda }}=0;}

o equivalente

{displaystyle {frac { partial f(x) }{partial x}}+lambda cdot {frac { partial g(x) }{partial x}}=0qquad }

{displaystyle qquad g(x)=0~.}

La solución correspondiente a la optimización restringida original es siempre un punto silla de la función Lagrangiana, que se puede identificar entre los puntos estacionarios a partir de la definición de la matriz hessiana bordeada.

La gran ventaja de este método es que permite que la optimización se resuelva sin parametrización explícita en términos de las limitaciones. Como resultado, el método de multiplicadores Lagrange es ampliamente utilizado para resolver problemas de optimización limitados desafiantes. Además, el método de multiplicadores Lagrange se generaliza por las condiciones Karush-Kuhn-Tucker, que también pueden tener en cuenta las limitaciones de desigualdad de la forma ${displaystyle h(mathbf {x})leq c }$ para una constante dada ${displaystyle c~.}$

Declaración

Lo siguiente se conoce como el teorema del multiplicador de Lagrange.

Vamos ${displaystyle fcolon mathbb {R} ^{n}rightarrow mathbb {R} }$ ser la función objetiva, ${displaystyle gcolon mathbb {R} ^{n}rightarrow mathbb {R} ^{c} }$ ser la función de limitaciones, ambas pertenecientes a $C^{1}$ (es decir, teniendo los primeros derivados continuos). Vamos ${displaystyle x_{star } }$ ser una solución óptima para el siguiente problema de optimización tal que $<math alttext="{displaystyle operatorname {rank} (operatorname {D} g(x_{star }))=crango⁡ ⁡ ()D⁡ ⁡ g()x⋆ ⋆ ))=c.n{displaystyle \operatorname {rank} (operatorname {D} g(x_{star })=c won }<img alt="{displaystyle operatorname {rank} (operatorname {D} g(x_{star }))=c$ (Aquí) ${displaystyle operatorname {D} g(x_{star }) }$ denota la matriz de derivados parciales, ${displaystyle {Bigl [}operatorname {D} g(x_{star }){Bigr ]}_{j,k}=left[{frac { partial g_{j} }{partial x_{k}}}right] }$ ):

{displaystyle {text{maximize}} f(x)}

{displaystyle {text{subject to:}} g(x)=0}

Entonces existe un multiplicador Lagrange único ${displaystyle lambda _{star }in mathbb {R} ^{c} }$ tales que ${displaystyle operatorname {D} f(x_{star })=lambda _{star }^{mathsf {T}}operatorname {D} g(x_{star })~.}$

El teorema del multiplicador de Lagrange establece que en cualquier máximo (o mínimo) local de la función evaluada bajo las restricciones de igualdad, si se aplica la calificación de la restricción (se explica a continuación), entonces el gradiente de la función (en ese punto) se puede expresar como una combinación lineal de los gradientes de las restricciones (en ese punto), con los multiplicadores de Lagrange actuando como coeficientes. Esto equivale a decir que cualquier dirección perpendicular a todos los gradientes de las restricciones también es perpendicular al gradiente de la función. O aún, decir que la derivada direccional de la función es $0$ en todas las direcciones factibles.

Restricción única

Gráfico 1: La curva roja muestra la limitación

g () x, Sí.) c

. Las curvas azules son contornos de

f () x, Sí.)

. El punto en el que la restricción roja tangencialmente toca un contorno azul es el máximo

f () x, Sí.)

a lo largo de la restricción, desde

d 1 ■ d 2

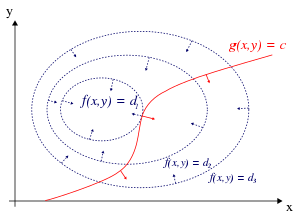
Para el caso de una sola restricción y solo dos variables de elección (como se ejemplifica en la Figura 1), considere el problema de optimización

{displaystyle {text{maximize}} f(x,y)}

{displaystyle {text{subject to:}} g(x,y)=0}

(A veces una constante aditiva se muestra por separado en lugar de ser incluido en $g$ , en cuyo caso se escribe la restricción ${displaystyle g(x,y)=c}$ como en la figura 1.) Asumimos que ambos ${displaystyle f }$ y $g$ tienen derivados parciales continuos. Presentamos una nueva variable ( $lambda$ Se llama Multiplicador Lagrange (o Multiplicador indeterminado) y estudiar el Función de separación (o Lagrangian o Lagrangian expression) definido por

{displaystyle {mathcal {L}}(x,y,lambda)=f(x,y)+lambda cdot g(x,y),}

Donde ${displaystyle lambda }$ el término puede ser añadido o restado. Si ${displaystyle f(x_{0},y_{0}) }$ es un máximo ${displaystyle f(x,y) }$ para el problema inicial y ${displaystyle nabla g(x_{0},y_{0})neq 0}$ entonces existe ${displaystyle lambda _{0} }$ tal que ( ${displaystyle x_{0},y_{0},lambda _{0} }$ ) es un Punto fijo para la función Lagrange (puntos estecionarios son aquellos puntos donde los primeros derivados parciales de ${displaystyle {mathcal {L}} }$ son cero). Suposición ${displaystyle nabla gneq 0 }$ se llama calificación restrictiva. Sin embargo, no todos los puntos estacionarios producen una solución del problema original, ya que el método de multiplicadores Lagrange produce sólo una condición necesaria para la óptimaidad en problemas limitados. Existen condiciones suficientes para un mínimo o máximo, pero si una solución de candidato en particular satisface las condiciones suficientes, sólo se garantiza que esa solución sea la mejor. localmente – es decir, es mejor que cualquier punto cercano admisible. El mundial óptimo se puede encontrar comparando los valores de la función objetiva original en los puntos que satisfacen las condiciones necesarias y locales suficientes.

El método de los multiplicadores de Lagrange se basa en la intuición de que, como máximo, $f (x, y)$ no puede aumentar en la dirección de ningún punto vecino que también tenga $g = 0$ . Si lo fuera, podríamos caminar a lo largo de $g = 0$ para llegar más alto, lo que significa que el punto de partida no era en realidad el máximo. Visto de esta manera, es un análogo exacto a probar si la derivada de una función sin restricciones es $0$ , es decir, estamos verificando que la derivada direccional es 0 en cualquier (dirección viable).

Podemos visualizar contornos de $f$ dados por $f (x, y) = d$ para varios valores de $d$ , y el contorno de $g$ dado por $g (x, y) = c$ .

Supongamos que caminamos a lo largo de la línea de contorno con $g = c$ . Nos interesa encontrar puntos donde $f$ casi no cambia mientras caminamos, ya que estos puntos pueden ser máximos.

Hay dos formas en que esto podría suceder:

Podríamos tocar una línea de contorno $f$ , ya que por definición $f$ no cambia mientras caminamos por sus líneas de contorno. Esto significaría que los tangentes a las líneas de contorno $f$ y $g$ son paralelos aquí.
Hemos alcanzado una parte "nivel" de $f$ , significa que $f$ no cambia en ninguna dirección.

Para comprobar la primera posibilidad (tocamos una línea de contorno de $f$ ), observe que dado que el gradiente de una función es perpendiculares a las curvas de nivel, las tangentes a las curvas de nivel de $f$ y $g$ son paralelos si y solo si los gradientes de $f$ y $g$ son paralelas. Por lo tanto, queremos puntos $(x, y)$ donde $g (x, y) = c$ y

{displaystyle nabla _{x,y}f=lambda ,nabla _{x,y}g,}

para algunos $lambda$

dónde

{displaystyle nabla _{x,y}f=left({frac {partial f}{partial x}},{frac {partial f}{partial y}}right),qquad nabla _{x,y}g=left({frac {partial g}{partial x}},{frac {partial g}{partial y}}right)}

son los respectivos gradientes. La constante $lambda$ se requiere porque aunque los dos vectores gradientes son paralelos, las magnitudes de los vectores gradientes generalmente no son iguales. Esta constante se llama el multiplicador Lagrange. (En algunas convenciones ${displaystyle lambda }$ es precedido por un signo menos).

Observe que este método también resuelve la segunda posibilidad, que $f$ es nivel: si $f$ es nivel, entonces su gradiente es cero, y el ajuste $lambda =0$ es una solución independientemente de ${displaystyle nabla _{x,y}g}$ .

Para incorporar estas condiciones en una ecuación, introducimos una función auxiliar

{displaystyle {mathcal {L}}(x,y,lambda)equiv f(x,y)+lambda cdot g(x,y)}

y resolver

{displaystyle nabla _{x,y,lambda }{mathcal {L}}(x,y,lambda)=0~.}

Tenga en cuenta que esto equivale a resolver tres ecuaciones con tres incógnitas. Este es el método de los multiplicadores de Lagrange.

Note que ${displaystyle nabla _{lambda }{mathcal {L}}(x,y,lambda)=0 }$ implicación ${displaystyle g(x,y)=0}$ como el derivado parcial de ${mathcal {L}}$ con respecto a $lambda$ es ${displaystyle -g(x,y)}$ que claramente es cero si ${displaystyle g(x,y)=0~.}$

Para resumir

{displaystyle nabla _{x,y,lambda }{mathcal {L}}(x,y,lambda)=0iff {begin{cases}nabla _{x,y}f(x,y)=lambda ,nabla _{x,y}g(x,y)\g(x,y)=0end{cases}}}

El método generaliza fácilmente las funciones en $n$ variables

{displaystyle nabla _{x_{1},dotsx_{n},lambda }{mathcal {L}}(x_{1},dotsx_{n},lambda)=0}

lo que equivale a resolver $n + 1$ ecuaciones en $n + 1$ incógnitas.

La extrema restringida $f$ son Puntos críticos de la Lagrangia ${mathcal {L}}$ , pero no son necesariamente local extrema de ${displaystyle {mathcal {L}} }$ (véase el ejemplo 2 infra).

Se puede reformular el lagrangiano como un hamiltoniano, en cuyo caso las soluciones son mínimos locales para el hamiltoniano. Esto se hace en la teoría del control óptimo, en la forma del principio mínimo de Pontryagin.

El hecho de que las soluciones del Lagrangiano no sean necesariamente extremos también plantea dificultades para la optimización numérica. Esto se puede abordar calculando la magnitud del gradiente, ya que los ceros de la magnitud son necesariamente mínimos locales, como se ilustra en el ejemplo de optimización numérica.

Múltiples restricciones

Figura 2: Un paraboloide limitado en dos líneas de intersección.

Figura 3: Mapa de Contorno de la Figura 2.

El método de multiplicadores Lagrange se puede ampliar para resolver problemas con múltiples restricciones utilizando un argumento similar. Considere un paraboloide sujeto a dos limitaciones de línea que se intersectan en un solo punto. Como única solución viable, este punto es obviamente un extremum limitado. Sin embargo, el nivel establecido ${displaystyle f }$ claramente no es paralelo a ninguna limitación en el punto de intersección (ver Figura 3); en cambio, es una combinación lineal de los dos gradientes de las limitaciones. En el caso de múltiples limitaciones, eso será lo que buscamos en general: El método de Lagrange busca puntos no en los que el gradiente de ${displaystyle f }$ es una combinación lineal de todos los gradientes de las limitaciones.

Concretamente, supongo que tenemos $M$ restricciones y están caminando por el conjunto de puntos que satisfacen ${displaystyle g_{i}(mathbf {x})=0,i=1,dotsM~.}$ Cada punto ${displaystyle mathbf {x} }$ sobre el contorno de una función de limitación determinada $g_{i}$ tiene un espacio de direcciones permitido: el espacio de vectores perpendiculares a ${displaystyle nabla g_{i}(mathbf {x}).}$ El conjunto de direcciones que son permitidas por todas las restricciones es por lo tanto el espacio de direcciones perpendiculares a todos los gradientes de las limitaciones. Denota este espacio de movimientos permitidos por ${displaystyle A }$ y denota el lapso de los gradientes de las limitaciones por ${displaystyle S~.}$ Entonces... ${displaystyle A=S^{perp }}$ el espacio de vectores perpendicular a cada elemento de ${displaystyle S~.}$

Todavía estamos interesados en encontrar puntos donde ${displaystyle f }$ no cambia a medida que caminamos, ya que estos puntos podrían ser (construidos) extrema. Por lo tanto, buscamos ${displaystyle mathbf {x} }$ tal que cualquier dirección permitida de movimiento lejos de $mathbf {x}$ es perpendicular a ${displaystyle nabla f(mathbf {x}) }$ (Otra vez podríamos aumentar $f$ moviéndose a lo largo de esa dirección permitible). En otras palabras, ${displaystyle nabla f(mathbf {x})in A^{perp }=S~.}$ Así que hay escalares ${displaystyle lambda _{1},lambda _{2},...lambda _{M} }$ tales que

{displaystyle nabla f(mathbf {x})=sum _{k=1}^{M}lambda _{k},nabla g_{k}(mathbf {x})quad iff quad nabla f(mathbf {x})-sum _{k=1}^{M}{lambda _{k}nabla g_{k}(mathbf {x})}=0~.}

Estos cuero cabelludos son los multiplicadores Lagrange. Ahora tenemos $M$ de ellos, uno por cada limitación.

Como antes, introducimos una función auxiliar

{displaystyle {mathcal {L}}left(x_{1},ldotsx_{n},lambda _{1},ldotslambda _{M}right)=fleft(x_{1},ldotsx_{n}right)-sum limits _{k=1}^{M}{lambda _{k}g_{k}left(x_{1},ldotsx_{n}right)} }

y resolver

{displaystyle nabla _{x_{1},ldotsx_{n},lambda _{1},ldotslambda _{M}}{mathcal {L}}(x_{1},ldotsx_{n},lambda _{1},ldotslambda _{M})=0iff {begin{cases}nabla f(mathbf {x})-sum _{k=1}^{M}{lambda _{k},nabla g_{k}(mathbf {x})}=0\g_{1}(mathbf {x})=cdots =g_{M}(mathbf {x})=0end{cases}}}

que asciende a la solución ${displaystyle n+M }$ ecuaciones en ${displaystyle n+M }$ desconocidos.

La suposición de calificación de restricción cuando hay múltiples restricciones es que los gradientes de restricción en el punto relevante son linealmente independientes.

Formulación moderna a través de variedades diferenciables

El problema de encontrar la máxima local y el minima sujeto a restricciones se puede generalizar para encontrar la máxima local y el minima en un múltiple diferente ${displaystyle M~.}$ En lo que sigue, no es necesario que $M$ ser un espacio euclidiano, o incluso un manifold Riemanniano. Todas las apariencias del gradiente ${displaystyle nabla }$ (que depende de la elección de la métrica Riemanniana) puede ser reemplazada por el derivado exterior ${displaystyle operatorname {d} ~.}$

Restricción única

Vamos $M$ ser un conjunto suave de la dimensión ${displaystyle m~.}$ Supongamos que deseamos encontrar los puntos estacionarios ${displaystyle x }$ de una función lisa ${displaystyle f:Mto mathbb {R} }$ cuando se restringe al submanifold ${displaystyle N }$ definidas por ${displaystyle g(x)=0}$ Donde ${displaystyle g:Mto mathbb {R} }$ es una función suave para la cual $0$ es un valor regular.

Vamos ${displaystyle operatorname {d} f }$ y ${displaystyle operatorname {d} g }$ ser los derivados exteriores de ${displaystyle f }$ y $g$ . Estabilidad para la restricción ${displaystyle f|_{N} }$ a ${displaystyle xin N }$ medios ${displaystyle operatorname {d} (f|_{N})_{x}=0~.}$ Equivalentemente, el núcleo ${displaystyle ker(operatorname {d} f_{x}) }$ contiene ${displaystyle T_{x}N=ker(operatorname {d} g_{x})~.}$ En otras palabras, ${displaystyle operatorname {d} f_{x} }$ y ${displaystyle operatorname {d} g_{x} }$ son proporcionales 1-formas. Para ello es necesario y suficiente que el siguiente sistema ${displaystyle {tfrac {1}{2}}m(m-1) }$ ecuaciones sostiene:

{displaystyle operatorname {d} f_{x}wedge operatorname {d} g_{x}=0in Lambda ^{2}(T_{star x}M)}

Donde ${displaystyle wedge }$ denota el producto exterior. Los puntos fijos ${displaystyle x }$ son las soluciones del sistema anterior de ecuaciones más la limitación ${displaystyle g(x)=0~.}$ Note que ${displaystyle {tfrac {1}{2}}m(m-1) }$ ecuaciones no son independientes, ya que el lado izquierdo de la ecuación pertenece a la subvariedad de ${displaystyle Lambda ^{2}(T_{star x}M) }$ consistente en elementos descompuestos.

En esta formulación, no es necesario encontrar explícitamente el multiplicador Lagrange, un número ${displaystyle lambda }$ tales que ${displaystyle operatorname {d} f_{x}=lambda cdot operatorname {d} g_{x}~.}$

Múltiples restricciones

Vamos $M$ y ${displaystyle f }$ como en la sección anterior relativa al caso de una sola limitación. Más que la función $g$ descrito allí, ahora considerar una función suave $1)}" xmlns="http://www.w3.org/1998/Math/MathML">G:M→ → Rp()p■1),{displaystyle G:Mto mathbb [R] ^{p}(p]1)}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/30f319767ea2333871e48baa3aa5f20113618782" style="vertical-align: -0.838ex; width:21.605ex; height:2.843ex;"/>$ con funciones componentes ${displaystyle g_{i}:Mto mathbb {R} }$ para la cual ${displaystyle 0in mathbb {R} ^{p}}$ es un valor regular. Vamos $N$ ser el submanifold de $M$ definidas por ${displaystyle G(x)=0~.}$

${displaystyle x }$ es un punto estacionario ${displaystyle f|_{N}}$ si ${displaystyle ker(operatorname {d} f_{x}) }$ contiene ${displaystyle ker(operatorname {d} G_{x})~.}$ Para mayor comodidad ${displaystyle L_{x}=operatorname {d} f_{x} }$ y ${displaystyle K_{x}=operatorname {d} G_{x}}$ Donde ${displaystyle operatorname {d} G}$ denota el mapa tangente o Jacobian ${displaystyle TMto Tmathbb {R} ^{p}~.}$ El subespacio ${displaystyle ker(K_{x})}$ tiene dimensión menor que la de ${displaystyle ker(L_{x})}$ , a saber ${displaystyle dim(ker(L_{x}))=n-1 }$ y ${displaystyle dim(ker(K_{x}))=n-p~.}$ ${displaystyle ker(K_{x})}$ pertenece ${displaystyle ker(L_{x}) }$ si ${displaystyle L_{x}in T_{star x}M}$ pertenece a la imagen de ${displaystyle K_{star x}:mathbb {R} _{star }^{p}to T_{star x}M~.}$ Computationally speaking, the condition is that $L_{x}$ pertenece al espacio de fila de la matriz ${displaystyle K_{x}}$ o equivalentemente el espacio de la columna de la matriz ${displaystyle K_{star x}}$ (la transposición). Si ${displaystyle omega _{x}in Lambda ^{p}(T_{star x}M) }$ denota el producto exterior de las columnas de la matriz de ${displaystyle K_{star x}}$ la condición estacionaria para ${displaystyle f|_{N} }$ a ${displaystyle x }$ se convierte en

{displaystyle L_{x}wedge omega _{x}=0in Lambda ^{p+1}left(T_{star x}Mright)}

Una vez más, en esta formulación no es necesario encontrar explícitamente los multiplicadores Lagrange, los números ${displaystyle lambda _{1},ldotslambda _{p} }$ tales que

{displaystyle operatorname {d} f_{x}=sum _{i=1}^{p}lambda _{i}operatorname {d} (g_{i})_{x}~.}

Interpretación de los multiplicadores de Lagrange

En esta sección, modificamos las ecuaciones de restricción de la forma ${displaystyle g_{i}({bf {x}})=0}$ a la forma ${displaystyle g_{i}({bf {x}})=c_{i}}$ Donde ${displaystyle c_{i} }$ son $m$ constantes reales que se consideran argumentos adicionales de la expresión lagrangiana ${mathcal {L}}$ .

A menudo, los multiplicadores de Lagrange tienen una interpretación como alguna cantidad de interés. Por ejemplo, parametrizando la línea de contorno de la restricción, es decir, si la expresión lagrangiana es

{displaystyle {begin{aligned}&{mathcal {L}}(x_{1},x_{2},ldots;lambda _{1},lambda _{2},ldots;c_{1},c_{2},ldots)\[4pt]={}&f(x_{1},x_{2},ldots)+lambda _{1}(c_{1}-g_{1}(x_{1},x_{2},ldots))+lambda _{2}(c_{2}-g_{2}(x_{1},x_{2},dots))+cdots end{aligned}}}

entonces

{displaystyle {frac {partial {mathcal {L}}}{partial c_{k}}}=lambda _{k}~.}

Entonces, $λ k$ es la tasa de cambio de la cantidad que se optimiza como una función del parámetro de restricción. Como ejemplos, en la mecánica lagrangiana, las ecuaciones de movimiento se derivan al encontrar puntos estacionarios de la acción, la integral de tiempo de la diferencia entre energía cinética y potencial. Por lo tanto, la fuerza sobre una partícula debido a un potencial escalar, $F = -\nabla V$ , puede interpretarse como un Multiplicador de Lagrange que determina el cambio de acción (transferencia de potencial a energía cinética) después de una variación en la trayectoria restringida de la partícula. En la teoría de control, esto se formula en cambio como ecuaciones de costate.

Además, por el teorema de sobre el valor óptimo de un multiplicador Lagrange tiene una interpretación como el efecto marginal de la constante de restricción correspondiente sobre el valor óptimo alcanzable de la función objetiva original: Si denotamos valores en el óptimo con una estrella ( $star$ ), entonces se puede demostrar que

{displaystyle {frac { operatorname {d} fleft( x_{1star }(c_{1},c_{2},dots), x_{2star }(c_{1},c_{2},dots), dots right) }{operatorname {d} c_{k}}}=lambda _{star k}~.}

Por ejemplo, en economía el beneficio óptimo para un jugador se calcula sujeto a un espacio limitado de acciones, donde un multiplicador Lagrange es el cambio en el valor óptimo de la función objetiva (beneficio) debido a la relajación de una determinada limitación (por ejemplo, a través de un cambio de ingreso); en tal contexto ${displaystyle lambda _{star k} }$ es el costo marginal de la restricción, y se conoce como el precio de sombra.

Condiciones suficientes

Se pueden establecer condiciones suficientes para un máximo o mínimo local restringido en términos de una secuencia de menores principales (determinantes de submatrices justificadas en la parte superior izquierda) de la matriz hessiana bordeada de segundas derivadas de la expresión lagrangiana.

Ejemplos

Ejemplo 1

Ilustración del problema de optimización restringido1

Supongamos que deseamos maximizar ${displaystyle f(x,y)=x+y }$ sujeto a la limitación ${displaystyle x^{2}+y^{2}=1~.}$ El conjunto factible es el círculo de unidad, y los conjuntos de nivel $f$ son líneas diagonales (con pendiente −1), por lo que podemos ver gráficamente que el máximo ocurre en ${displaystyle left({tfrac {1}{sqrt {2}}},{tfrac {1}{sqrt {2}}}right)}$ y que el mínimo ocurre ${displaystyle left(-{tfrac {1}{sqrt {2}}},-{tfrac {1}{sqrt {2}}}right)~.}$

Para el método de los multiplicadores de Lagrange, la restricción es

{displaystyle g(x,y)=x^{2}+y^{2}-1=0}

de ahí la función lagrangiana,

{displaystyle {begin{aligned}{mathcal {L}}(x,y,lambda)&=f(x,y)+lambda cdot g(x,y)\[4pt]&=x+y+lambda (x^{2}+y^{2}-1)\end{aligned}}}

es una función que equivale a ${displaystyle f(x,y) }$ cuando ${displaystyle g(x,y) }$ se establece $0$ .

Ahora podemos calcular el gradiente:

{displaystyle {begin{aligned}nabla _{x,y,lambda }{mathcal {L}}(x,y,lambda)&=left({frac {partial {mathcal {L}}}{partial x}},{frac {partial {mathcal {L}}}{partial y}},{frac {partial {mathcal {L}}}{partial lambda }}right)\[4pt]&=left(1+2lambda x,1+2lambda y,x^{2}+y^{2}-1right) color {gray}{,}end{aligned}}}

y por lo tanto:

{displaystyle nabla _{x,y,lambda }{mathcal {L}}(x,y,lambda)=0quad Leftrightarrow quad {begin{cases}1+2lambda x=0\1+2lambda y=0\x^{2}+y^{2}-1=0end{cases}}}

Observe que la última ecuación es la restricción original.

Las dos primeras ecuaciones producen

{displaystyle x=y=-{frac {1}{2lambda }},qquad lambda neq 0~.}

Sustituyendo en la última ecuación tenemos:

{displaystyle {frac {1}{4lambda ^{2}}}+{frac {1}{4lambda ^{2}}}-1=0}

entonces

{displaystyle lambda =pm {frac {1}{sqrt {2 }}}}

que implica que los puntos estacionarios de ${mathcal {L}}$ son

{displaystyle left({tfrac {sqrt {2 }}{2}},{tfrac {sqrt {2 }}{2}},-{tfrac {1}{sqrt {2 }}}right),qquad left(-{tfrac {sqrt {2 }}{2}},-{tfrac {sqrt {2 }}{2}},{tfrac {1}{sqrt {2 }}}right)~.}

Evaluar la función objetivo $f$ en estos puntos produce

{displaystyle fleft({tfrac {sqrt {2 }}{2}},{tfrac {sqrt {2 }}{2}}right)={sqrt {2 }}\qquad fleft(-{tfrac {sqrt {2 }}{2}},-{tfrac {sqrt {2 }}{2}}right)=-{sqrt {2 }}~.}

Así el máximo limitado es ${displaystyle {sqrt {2 }} }$ y el mínimo limitado $-{sqrt {2}}$ .

Ejemplo 2

Ilustración del problema de optimización restringido2

Ahora modificamos la función objetiva del Ejemplo1 así que minimizamos ${displaystyle f(x,y)=(x+y)^{2} }$ en lugar de ${displaystyle f(x,y)=x+y}$ otra vez a lo largo del círculo ${displaystyle g(x,y)=x^{2}+y^{2}-1=0~.}$ Ahora el nivel se establece $f$ son todavía líneas de pendiente -1, y los puntos en el círculo tangente a estos conjuntos de nivel son de nuevo ${displaystyle ({sqrt {2}}/2,{sqrt {2}}/2) }$ y ${displaystyle (-{sqrt {2}}/2,-{sqrt {2}}/2)~.}$ Estos puntos de tangencia son máximas ${displaystyle f~.}$

Por otro lado, la minima ocurre en el nivel establecido para ${displaystyle f=0 }$ (desde su construcción ${displaystyle f }$ no puede tomar valores negativos, a ${displaystyle ({sqrt {2}}/2,-{sqrt {2}}/2) }$ y ${displaystyle (-{sqrt {2}}/2,{sqrt {2}}/2)}$ donde las curvas de nivel ${displaystyle f }$ no son tangentes a la restricción. La condición de que ${displaystyle nabla _{x,y,lambda }left(f(x,y)+lambda cdot g(x,y)right)=0 }$ correctamente identifica los cuatro puntos como extremos; la minima se caracteriza por ${displaystyle lambda =0 }$ y la máxima ${displaystyle lambda =-2~.}$

Ejemplo 3

Ilustración del problema de optimización restringido3.

Este ejemplo trata con cálculos más extenuantes, pero sigue siendo un problema de restricción única.

Supongamos que uno quiere encontrar los valores máximos de

f(x,y)=x^{2}y

con la condición de que ${displaystyle x }$ - y ${displaystyle y }$ -coordinados se encuentran en el círculo alrededor del origen con radio ${displaystyle {sqrt {3 }}~.}$ Es decir, sujeto a la limitación

{displaystyle g(x,y)=x^{2}+y^{2}-3=0~.}

Como sólo hay una sola limitación, hay un solo multiplicador, dicen ${displaystyle lambda ~.}$

La limitación ${displaystyle g(x,y) }$ es idéntico cero en el círculo del radio ${displaystyle {sqrt {3 }}~.}$ Cualquier múltiplo de ${displaystyle g(x,y) }$ se puede añadir a ${displaystyle g(x,y) }$ salir ${displaystyle g(x,y) }$ sin cambios en la región de interés (en el círculo donde nuestra limitación original está satisfecha).

Aplicando el método ordinario del multiplicador de Lagrange se obtiene

{displaystyle {begin{aligned}{mathcal {L}}(x,y,lambda)&=f(x,y)+lambda cdot g(x,y)\&=x^{2}y+lambda (x^{2}+y^{2}-3)\end{aligned}}}

a partir del cual se puede calcular el gradiente:

{displaystyle {begin{aligned}nabla _{x,y,lambda }{mathcal {L}}(x,y,lambda)&=left({frac {partial {mathcal {L}}}{partial x}},{frac {partial {mathcal {L}}}{partial y}},{frac {partial {mathcal {L}}}{partial lambda }}right)\&=left(2xy+2lambda x,x^{2}+2lambda y,x^{2}+y^{2}-3right)~.end{aligned}}}

Y por lo tanto:

{displaystyle nabla _{x,y,lambda }{mathcal {L}}(x,y,lambda)=0quad iff quad {begin{cases}2xy+2lambda x=0\x^{2}+2lambda y=0\x^{2}+y^{2}-3=0end{cases}}quad iff quad {begin{cases}x(y+lambda)=0&{text{(i)}}\x^{2}=-2lambda y&{text{(ii)}}\x^{2}+y^{2}=3&{text{(iii)}}end{cases}}}

iii) es sólo la limitación original. i) implica ${displaystyle x=0 }$ o ${displaystyle lambda =-y~.}$ Si $x=0$ entonces ${displaystyle y=pm {sqrt {3 }} }$ por iii) y en consecuencia ${displaystyle lambda =0 }$ de ii). Si ${displaystyle lambda =-y}$ sustituyendo esto a ii) rendimientos ${displaystyle x^{2}=2y^{2}~.}$ Sustituir esto en iii) y resolver ${displaystyle y }$ da ${displaystyle y=pm 1~.}$ Por lo tanto hay seis puntos críticos ${displaystyle {mathcal {L}}:}$

{displaystyle ({sqrt {2 }},1,-1);quad (-{sqrt {2 }},1,-1);quad ({sqrt {2 }},-1,1);quad (-{sqrt {2 }},-1,1);quad (0,{sqrt {3 }},0);quad (0,-{sqrt {3 }},0)~.}

Al evaluar el objetivo en estos puntos, se encuentra que

{displaystyle f(pm {sqrt {2 }},1)=2;quad f(pm {sqrt {2 }},-1)=-2;quad f(0,pm {sqrt {3 }})=0~.}

Por consiguiente, la función objetiva alcanza el máximo global (sujeto a las limitaciones) ${displaystyle (pm {sqrt {2 }},1)}$ y el mínimo mundial ${displaystyle (pm {sqrt {2 }},-1)~.}$ El punto ${displaystyle (0,{sqrt {3 }}) }$ es un mínimo local ${displaystyle f }$ y ${displaystyle (0,-{sqrt {3 }}) }$ es un máximo local ${displaystyle f}$ como puede determinarse por consideración de la matriz hesiana ${displaystyle {mathcal {L}}(x,y,0)~.}$

Note que mientras ${displaystyle ({sqrt {2 }},1,-1) }$ es un punto crítico ${displaystyle {mathcal {L}}}$ no es un extremum local ${displaystyle {mathcal {L}}~.}$ Tenemos

{displaystyle {mathcal {L}}left({sqrt {2 }}+varepsilon1,-1+delta right)=2+delta left(varepsilon ^{2}+left(2{sqrt {2 }}right)varepsilon right)~.}

Dado cualquier barrio ${displaystyle ({sqrt {2 }},1,-1)}$ uno puede elegir un pequeño positivo ${displaystyle varepsilon }$ y un pequeño ${displaystyle delta }$ de cualquier signo para conseguir ${displaystyle {mathcal {L}}}$ valores tanto mayores como inferiores ${displaystyle 2~.}$ Esto también se puede ver desde la matriz hesiana ${displaystyle {mathcal {L}} }$ evaluada en este punto (o de hecho en cualquiera de los puntos críticos) que es una matriz indefinida. Cada uno de los puntos críticos ${displaystyle {mathcal {L}} }$ es un punto de silla ${displaystyle {mathcal {L}}~.}$

Ejemplo 4

Entropy

Supongamos que deseamos encontrar la distribución discreta de probabilidad en los puntos ${displaystyle {p_{1},p_{2},ldotsp_{n}} }$ con máxima información entropía. Esto es lo mismo que decir que deseamos encontrar la distribución de probabilidad menos estructurada en los puntos ${displaystyle {p_{1},p_{2},cdotsp_{n}}~.}$ En otras palabras, deseamos maximizar la ecuación entropía de Shannon:

{displaystyle f(p_{1},p_{2},ldotsp_{n})=-sum _{j=1}^{n}p_{j}log _{2}p_{j}~.}

Para que esto sea una distribución de probabilidad la suma de las probabilidades ${displaystyle p_{i} }$ en cada punto ${displaystyle x_{i} }$ debe igual 1, por lo que nuestra limitación es:

{displaystyle g(p_{1},p_{2},ldotsp_{n})=sum _{j=1}^{n}p_{j}=1~.}

Usamos multiplicadores Lagrange para encontrar el punto de máxima entropía, ${displaystyle {vec {p}}^{,*}}$ en todas las distribuciones discretas de probabilidad ${displaystyle {vec {p}} }$ on ${displaystyle {x_{1},x_{2},ldotsx_{n}}~.}$ Requerimos que:

{displaystyle left.{frac {partial }{partial {vec {p}}}}(f+lambda (g-1))right|_{{vec {p}}={vec {p}}^{,*}}=0}

que da un sistema de $n$ ecuaciones, ${displaystyle k=1, ldotsn}$ tal que:

{displaystyle left.{frac {partial }{partial p_{k}}}left{-left(sum _{j=1}^{n}p_{j}log _{2}p_{j}right)+lambda left(sum _{j=1}^{n}p_{j}-1right)right}right|_{p_{k}=p_{star k}}=0~.}

Efectuando la diferenciación de estas $n$ ecuaciones, obtenemos

{displaystyle -left({frac {1}{ln 2}}+log _{2}p_{star k}right)+lambda =0~.}

Esto demuestra que todo ${displaystyle p_{star k} }$ son iguales (porque dependen de $λ$ solamente). Usando la restricción

{displaystyle sum _{j}p_{j}=1}

encontramos

{displaystyle p_{star k}={frac {1}{n}}~.}

Por lo tanto, la distribución uniforme es la distribución con mayor entropía, entre las distribuciones en $n$ puntos.

Ejemplo 5

Optimización numérica

Los multiplicadores Lagrange causan que los puntos críticos ocurran en los puntos de silla (Ejemplo5).

La magnitud del gradiente se puede utilizar para forzar los puntos críticos a ocurrir en minima local (Ejemplo5).

Los puntos críticos de los lagrangianos ocurren en los puntos de silla, en lugar de en los máximos (o mínimos) locales. Desafortunadamente, muchas técnicas de optimización numérica, como el ascenso de colinas, el descenso de gradientes, algunos de los métodos cuasi-Newton, entre otros, están diseñados para encontrar máximos (o mínimos) locales y no puntos de silla. Por esta razón, uno debe modificar la formulación para asegurarse de que sea un problema de minimización (por ejemplo, al extremar el cuadrado del gradiente del Lagrangiano como se muestra a continuación), o bien usar una técnica de optimización que encuentre puntos estacionarios (como como el método de Newton sin una búsqueda de línea de búsqueda de extremos) y no necesariamente extremos.

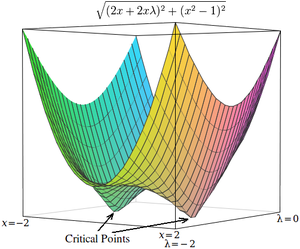
Como ejemplo simple, considere el problema de encontrar el valor $x$ que minimiza ${displaystyle f(x)=x^{2}}$ tales restricciones ${displaystyle x^{2}=1~.}$ (Este problema es algo poco típico porque sólo hay dos valores que satisfacen esta limitación, pero es útil para fines de ilustración porque la función no constreñida correspondiente puede ser visualizada en tres dimensiones.)

Usando multiplicadores de Lagrange, este problema se puede convertir en un problema de optimización sin restricciones:

{displaystyle {mathcal {L}}(x,lambda)=x^{2}+lambda (x^{2}-1)~.}

Los dos puntos críticos ocurren en puntos de silla donde $x = 1$ y $x = -1$ .

Para resolver este problema con una técnica de optimización numérica, primero debemos transformar este problema de modo que los puntos críticos ocurran en los mínimos locales. Esto se hace calculando la magnitud del gradiente del problema de optimización sin restricciones.

Primero, calculamos la derivada parcial del problema sin restricciones con respecto a cada variable:

{displaystyle {begin{aligned}&{frac {partial {mathcal {L}}}{partial x}}=2x+2xlambda \[5pt]&{frac {partial {mathcal {L}}}{partial lambda }}=x^{2}-1~.end{aligned}}}

Si la función objetivo no es fácilmente diferenciable, el diferencial con respecto a cada variable se puede aproximar como

{displaystyle {begin{aligned}{frac { partial {mathcal {L}} }{partial x}}approx {frac {{mathcal {L}}(x+varepsilonlambda)-{mathcal {L}}(x,lambda)}{varepsilon }},\[5pt]{frac { partial {mathcal {L}} }{partial lambda }}approx {frac {{mathcal {L}}(x,lambda +varepsilon)-{mathcal {L}}(x,lambda)}{varepsilon }},end{aligned}}}

Donde ${displaystyle varepsilon }$ es un pequeño valor.

A continuación, calculamos la magnitud del gradiente, que es la raíz cuadrada de la suma de los cuadrados de las derivadas parciales:

{displaystyle {begin{aligned}h(x,lambda)&={sqrt {(2x+2xlambda)^{2}+(x^{2}-1)^{2} }}\[4pt]&approx {sqrt {left({frac { {mathcal {L}}(x+varepsilonlambda)-{mathcal {L}}(x,lambda) }{varepsilon }}right)^{2}+left({frac { {mathcal {L}}(x,lambda +varepsilon)-{mathcal {L}}(x,lambda) }{varepsilon }}right)^{2} }}~.end{aligned}}}

(Dado que la magnitud siempre es no negativa, optimizar sobre la magnitud al cuadrado es equivalente a optimizar sobre la magnitud. Por lo tanto, la "raíz cuadrada" puede omitirse de estas ecuaciones sin que se espere una diferencia en la resultados de la optimización.)

Los puntos críticos $h$ ocurre en $x = 1$ y $x = 1 -$ , como en ${displaystyle {mathcal {L}}~.}$ A diferencia de los puntos críticos en ${displaystyle {mathcal {L}}}$ sin embargo, los puntos críticos en $h$ ocurre en minima local, por lo que las técnicas de optimización numérica se pueden utilizar para encontrarlas.

Aplicaciones

Teoría del control

En la teoría del control óptimo, los multiplicadores de Lagrange se interpretan como variables de coste y los multiplicadores de Lagrange se reformulan como la minimización del hamiltoniano, en el principio mínimo de Pontryagin.

Programación no lineal

El método del multiplicador de Lagrange tiene varias generalizaciones. En la programación no lineal existen varias reglas multiplicadoras, p. la regla del multiplicador de Carathéodory-John y la regla del multiplicador convexo, para restricciones de desigualdad.

Sistemas de energía

Los métodos basados en multiplicadores de Lagrange tienen aplicaciones en sistemas de potencia, p. en la colocación de recursos de energía distribuida (DER) y el deslastre de carga.

Contenido relacionado

Más resultados...