Muestreo por transformada inversa

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Método básico para muestreo número pseudo-aleatorio

Muestreo por transformada inversa (también conocido como muestreo por inversión, la transformada integral de probabilidad inversa, el método de transformación inversa, la transformada de Smirnov o la regla de oro) es un método básico para el muestreo de números pseudoaleatorios, es decir, para generar números de muestra al azar a partir de cualquier distribución de probabilidad dada su función de distribución.

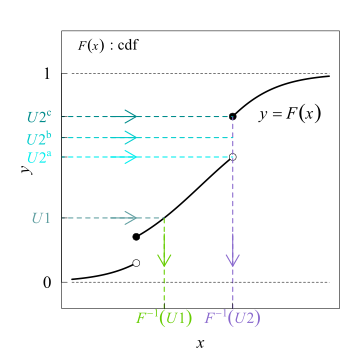
El muestreo de transformación inversa toma muestras uniformes de un número $u$ entre 0 y 1, interpretado como una probabilidad, y luego devuelve el menor número $xin {mathbb R}$ tales que ${displaystyle F(x)geq u}$ para la función de distribución acumulativa $F$ de una variable aleatoria. Por ejemplo, imagina que $F$ es la distribución normal estándar con media cero y desviación estándar uno. En el cuadro que figura a continuación se muestran las muestras tomadas de la distribución uniforme y su representación en la distribución normal estándar.

Transformación de la muestra uniforme a la normalidad
$u$	${displaystyle F^{-1}(u)}$
.5	0
.975	1.95996
.995	2.5758
.999999	4.75342
1-2⁻⁵²	8.12589

Muestra de transformación inversa para distribución normal

Estamos eligiendo aleatoriamente una proporción del área bajo la curva y devolviendo el número en el dominio de manera que exactamente esta proporción del área se encuentre a la izquierda de ese número. Intuitivamente, es poco probable que elijamos un número en el otro extremo de las cruces porque hay muy poca área en ellas que requeriría elegir un número muy cercano a cero o uno.

Desde el punto de vista computacional, este método implica calcular la función de cuantiles de la distribución; en otras palabras, calcular la función de distribución acumulativa (CDF) de la distribución (que asigna un número en el dominio a una probabilidad entre 0 y 1) y luego invertir esa funcion Esta es la fuente del término "inverso" o "inversión" en la mayoría de los nombres de este método. Tenga en cuenta que para una distribución discreta, calcular la CDF en general no es demasiado difícil: simplemente sumamos las probabilidades individuales para los distintos puntos de la distribución. Sin embargo, para una distribución continua, necesitamos integrar la función de densidad de probabilidad (PDF) de la distribución, lo que es imposible de hacer analíticamente para la mayoría de las distribuciones (incluida la distribución normal). Como resultado, este método puede ser computacionalmente ineficiente para muchas distribuciones y se prefieren otros métodos; sin embargo, es un método útil para construir muestreadores de aplicación más general, como los que se basan en el muestreo por rechazo.

Para la distribución normal, la falta de una expresión analítica para la función cuantil correspondiente significa que se pueden preferir otros métodos (p. ej., la transformada de Box-Muller) desde el punto de vista computacional. Suele ocurrir que, incluso para distribuciones simples, el método de muestreo por transformada inversa puede mejorarse: véase, por ejemplo, el algoritmo de ziggurat y el muestreo por rechazo. Por otro lado, es posible aproximar la función de cuantiles de la distribución normal con extrema precisión utilizando polinomios de grado moderado y, de hecho, el método para hacerlo es lo suficientemente rápido como para que el muestreo por inversión sea ahora el método predeterminado para el muestreo de una distribución normal. en el paquete estadístico R.

Declaración formal

Para cualquier variable aleatoria ${displaystyle Xin mathbb {R} }$ , la variable aleatoria ${displaystyle F_{X}^{-1}(U)}$ tiene la misma ley $X$ , donde ${displaystyle F_{X}^{-1}}$ es el inverso generalizado de la función de distribución acumulativa $F_{X}$ de $X$ y $U$ es uniforme $[0,1]$ .

Para variables aleatorias continuas, la transformación integral de probabilidad inversa es en efecto el inverso de la transformación integral de probabilidad, que afirma que para una variable aleatoria continua $X$ con función de distribución acumulativa $F_{X}$ , la variable aleatoria ${displaystyle U=F_{X}(X)}$ es uniforme $[0,1]$ .

Gráfico de la técnica de inversión de

x

F(x)

. En la parte inferior derecha vemos la función regular y en la parte superior dejó su inversión.

Intuición

Desde ${displaystyle Usim mathrm {Unif} [0,1]}$ , queremos generar $X$ con CDF ${displaystyle F_{X}(x).}$ Asumimos $F_X(x)$ ser una función continua y estrictamente creciente, que proporciona buena intuición.

Queremos ver si podemos encontrar una transformación estrictamente monotona ${displaystyle T:[0,1]mapsto mathbb {R} }$ , tal que ${displaystyle T(U){overset {d}{=}}X}$ . Tendremos

${displaystyle F_{X}(x)=Pr(Xleq x)=Pr(T(U)leq x)=Pr(Uleq T^{-1}(x))=T^{-1}(x),{text{ for }}xin mathbb {R}}$

donde el último paso utilizó ${displaystyle Pr(Uleq y)=y}$ cuando $U$ es uniforme $[0,1]$ .

Así que tenemos $F_{X}$ ser la función inversa de $T$ , o, equivalente ${displaystyle T(u)=F_{X}^{-1}(u),uin [0,1].}$

Por lo tanto, podemos generar $X$ desde ${displaystyle F_{X}^{-1}(U).}$

El método

Esquema del muestreo de transformación inversa. La función inversa de

{displaystyle y=F_{X}(x)}

puede definirse

{displaystyle F_{X}^{-1}(y)=mathrm {inf} {x|F_{X}(x)geq y}}

Una animación de cómo el muestreo de transformación inversa genera valores aleatorios normalmente distribuidos de valores aleatorios distribuidos uniformemente

El problema que resuelve el método de muestreo por transformada inversa es el siguiente:

Vamos $X$ ser una variable aleatoria cuya distribución puede ser descrita por la función de distribución acumulativa $F_{X}$ .
Queremos generar valores de $X$ que se distribuyen según esta distribución.

El método de muestreo por transformada inversa funciona de la siguiente manera:

Generar un número aleatorio $u$ de la distribución uniforme estándar en el intervalo $[0,1]$ Es decir, de ${displaystyle Usim mathrm {Unif} [0,1].}$
Encontrar el inverso generalizado del CDF deseado, es decir, ${displaystyle F_{X}^{-1}(u)}$ .
Computación ${displaystyle X'(u)=F_{X}^{-1}(u)}$ . La variable aleatoria computada ${displaystyle X'(U)}$ distribución $F_{X}$ y por consiguiente la misma ley $X$ .

Expresado de manera diferente, dada una función de distribución acumulativa $F_{X}$ y una variable uniforme ${displaystyle Uin [0,1]}$ , la variable aleatoria ${displaystyle X=F_{X}^{-1}(U)}$ tiene la distribución $F_{X}$ .

En el caso continuo, se puede dar un tratamiento de tales funciones inversas como objetos que satisfacen ecuaciones diferenciales. Algunas de estas ecuaciones diferenciales admiten soluciones explícitas en series de potencias, a pesar de su no linealidad.

Ejemplos

Como ejemplo, supongamos que tenemos una variable aleatoria ${displaystyle Usim mathrm {Unif} (0,1)}$ y una función de distribución acumulativa

{displaystyle {begin{aligned}F(x)=1-exp(-{sqrt {x}})end{aligned}}}

Para realizar una inversión queremos resolver para

{displaystyle F(F^{-1}(u))=u}

{displaystyle {begin{aligned}F(F^{-1}(u))&=u\1-exp left(-{sqrt {F^{-1}(u)}}right)&=u\F^{-1}(u)&=(-log(1-u))^{2}\&=(log(1-u))^{2}end{aligned}}}

Desde aquí realizaríamos los pasos uno, dos y tres.

Como otro ejemplo, utilizamos la distribución exponencial con ${displaystyle F_{X}(x)=1-e^{-lambda x}}$ para x ≥ 0 (y 0 de otro modo). Resolviendo y=F(x) obtenemos la función inversa

{displaystyle x=F^{-1}(y)=-{frac {1}{lambda }}ln(1-y).}

Significa que si dibujamos algo

y_{0}

de una

{displaystyle Usim mathrm {Unif} (0,1)}

y computación

{displaystyle x_{0}=F_{X}^{-1}(y_{0})=-{frac {1}{lambda }}ln(1-y_{0}),}

Esto

x_{0}

tiene distribución exponencial.

La idea se ilustra en el siguiente gráfico:

Números aleatorios y_i se generan a partir de una distribución uniforme entre 0 y 1, es decir, Y ~ U(0, 1). Se dibujan como puntos de color en el eje y. Cada uno de los puntos se mapea según x=F⁻¹(y), que se muestra con flechas grises por dos puntos de ejemplo. En este ejemplo, hemos utilizado una distribución exponencial. Por lo tanto, para x ≥ 0, la densidad de probabilidad es

{displaystyle varrho _{X}(x)=lambda e^{-lambda ,x}}

y la función de distribución acumulada

{displaystyle F(x)=1-e^{-lambda ,x}}

. Por lo tanto,

{displaystyle x=F^{-1}(y)=-{frac {ln(1-y)}{lambda }}}

. Podemos ver que usando este método, muchos puntos terminan cerca de 0 y sólo pocos puntos terminan teniendo altos valores x - tal como se espera para una distribución exponencial.

Tenga en cuenta que la distribución no cambia si empezamos con 1-y en lugar de y. Para fines computacionales, basta con generar números aleatorios y en [0, 1] y luego simplemente calcular

{displaystyle x=F^{-1}(y)=-{frac {1}{lambda }}ln(y).}

Prueba de corrección

Vamos $F$ ser una función de distribución acumulativa, y dejar $F^{-1}$ ser su función inversa generalizada (utilizando el infimum porque los CDF son débilmente monotónicos y recto-continua):

<math alttext="{displaystyle F^{-1}(u)=inf ;{xmid F(x)geq u}qquad (0<uF− − 1()u)=inf{}x▪ ▪ F()x)≥ ≥ u}()0.u.1).{displaystyle F^{-1}(u)=inf ;{xmid F(x)geq u}qquad (0 seleccionó a1). }<img alt="F^{{-1}}(u)=inf ;{xmid F(x)geq u}qquad (0<u

Claim: Si $U$ es una variable aleatoria uniforme $[0,1]$ entonces $F^{{-1}}(U)$ tiene $F$ como su CDF.

Prueba:

{displaystyle {begin{aligned}&Pr(F^{-1}(U)leq x)\&{}=Pr(Uleq F(x))quad &(F{text{ is right-continuous, so }}{u:F^{-1}(u)leq x}={u:uleq F(x)})\&{}=F(x)quad &({text{because }}Pr(Uleq u)=u,{text{ when U is uniform on}}[0,1])\end{aligned}}}

Distribución truncada

El muestreo de transformación inversa se puede extender simplemente a los casos de distribuciones truncadas en el intervalo $(a,b]$ sin el costo del muestreo de rechazo: el mismo algoritmo se puede seguir, pero en lugar de generar un número aleatorio $u$ distribuidos uniformemente entre 0 y 1, generar $u$ distribuidos uniformemente entre ${displaystyle F(a)}$ y $F(b)$ , y luego de nuevo tomar ${displaystyle F^{-1}(u)}$ .

Reducción del número de inversiones

Para obtener una gran cantidad de muestras, es necesario realizar la misma cantidad de inversiones de la distribución. Una forma posible de reducir el número de inversiones mientras se obtiene un gran número de muestras es la aplicación del denominado muestreador Monte Carlo de Colocación Estocástica (SCMC) dentro de un marco de expansión de caos polinomial. Esto nos permite generar cualquier número de muestras de Monte Carlo con solo unas pocas inversiones de la distribución original con muestras independientes de una variable para la cual las inversiones están analíticamente disponibles, por ejemplo, la variable normal estándar.

Contenido relacionado

Más resultados...