Movimiento superlumínico

En astronomía, el movimiento superluminal es el movimiento aparentemente más rápido que la luz que se observa en algunas radiogalaxias, objetos BL Lac, cuásares, blazares y recientemente también en algunas fuentes galácticas llamadas microcuásares. Las ráfagas de energía que se mueven a lo largo de los chorros relativistas emitidos por estos objetos pueden tener un movimiento propio que parece mayor que la velocidad de la luz. Se cree que todas estas fuentes contienen un agujero negro, responsable de la eyección de masa a altas velocidades. Los ecos de luz también pueden producir un aparente movimiento superlumínico.

Explicación

El movimiento superluminal ocurre como un caso especial de un fenómeno más general que surge de la diferencia entre la velocidad aparente de los objetos distantes que se mueven a través del cielo y su velocidad real medida en la fuente.

Al rastrear el movimiento de tales objetos a través del cielo, se puede obtener un cálculo ingenuo de su velocidad mediante una simple distancia dividida por el cálculo del tiempo. Si se conoce la distancia del objeto a la Tierra, se puede medir la velocidad angular del objeto y la velocidad se puede calcular ingenuamente mediante:

velocidad aparente = distancia al objeto × × {displaystyle times } Velocidad angular.

Este cálculo no arroja la velocidad real del objeto, ya que no tiene en cuenta el hecho de que la velocidad de la luz es finita. Al medir el movimiento de objetos distantes a través del cielo, hay un gran retraso de tiempo entre lo observado y lo ocurrido, debido a la gran distancia que tiene que recorrer la luz del objeto distante para llegar a nosotros. El error en el ingenuo cálculo anterior proviene del hecho de que cuando un objeto tiene un componente de velocidad dirigido hacia la Tierra, a medida que el objeto se acerca a la Tierra, el retraso de tiempo se vuelve menor. Esto significa que la velocidad aparente calculada anteriormente es mayor que la velocidad real. En consecuencia, si el objeto se aleja de la Tierra, el cálculo anterior subestima la velocidad real.

Este efecto en sí mismo generalmente no conduce a que se observe movimiento superluminal. Pero cuando la velocidad real del objeto es cercana a la velocidad de la luz, se puede observar que la velocidad aparente es mayor que la velocidad de la luz, como resultado del efecto anterior. A medida que la velocidad real del objeto se acerca a la velocidad de la luz, el efecto es más pronunciado a medida que aumenta la componente de la velocidad hacia la Tierra. Esto significa que en la mayoría de los casos, las partículas 'superluminales' Los objetos viajan casi directamente hacia la Tierra. Sin embargo, no es estrictamente necesario que esto sea así, y todavía se puede observar movimiento superluminal en objetos con velocidades apreciables que no están dirigidas hacia la Tierra.

El movimiento superluminal se observa con mayor frecuencia en dos chorros opuestos que emanan del núcleo de una estrella o un agujero negro. En este caso, un chorro se aleja y el otro se acerca a la Tierra. Si se observan desplazamientos Doppler en ambas fuentes, la velocidad y la distancia se pueden determinar independientemente de otras observaciones.

Algunas pruebas contrarias

As early as 1983, at the "superliminal workshop " held at Jodrell Bank Observatory, referring to the seven then-known superluminal jets,

Schilizzi... presentó mapas de resolución de arco-segundo [showing the large-scale outer jets]... que... han revelado la doble estructura exterior en todas menos una (3C 273) de las fuentes superluminales conocidas. Una vergüenza es que el tamaño promedio proyectado [en el cielo] de la estructura exterior no es menor que el de la población normal de fuentes de radio.

In other words, the jets are evidently not, on average, close to the Earth 's line-of-sight. (Their apparent length would appear much shorter if they were.)

En 1993, Thomson et al. sugirió que el chorro (exterior) del cuásar 3C 273 es casi colineal con la línea de visión de la Tierra. Se ha observado un movimiento superluminal de hasta ~9,6c a lo largo del chorro (interior) de este quásar.

Se ha observado un movimiento superluminal de hasta 6c en las partes internas del chorro de M87. Para explicar esto en términos del enfoque de “ángulo estrecho”; modelo, el chorro no debe estar a más de 19° de la línea de visión de la Tierra. Pero la evidencia sugiere que el chorro se encuentra en realidad a unos 43° de la línea de visión de la Tierra. El mismo grupo de científicos revisó posteriormente ese hallazgo y argumentó a favor de un movimiento masivo superluminal en el que está incrustado el chorro.

Suggestions of turbulence and/or "wide cones " in the inner parts of the jets have been put forward to try to counter such problems, and there seems to be some evidence for this.

Velocidad de la señal

El modelo identifica una diferencia entre la información transportada por la onda a su velocidad de señal c y la información sobre la tasa aparente de cambio de posición del frente de onda. Si se prevé un pulso de luz en una guía de ondas (tubo de vidrio) que se mueve a través del campo de visión de un observador, el pulso sólo puede moverse a c a través de la guía. Si ese pulso también se dirige hacia el observador, este recibirá esa información de onda, en c. Si la guía de ondas se mueve en la misma dirección que el pulso, cambia la información sobre su posición, transmitida al observador como emisiones laterales del pulso. Puede considerar que la velocidad de cambio de posición aparentemente representa un movimiento más rápido que c cuando se calcula, como el borde de una sombra a través de una superficie curva. Esta es una señal diferente, que contiene información diferente, al pulso y no rompe el segundo postulado de la relatividad especial. c se mantiene estrictamente en todos los campos locales.

Derivación de la velocidad aparente

Un jet relativista que sale del centro de un núcleo galáctico activo se mueve a lo largo de AB con una velocidad v, y se observa desde el punto O. At time t1{displaystyle T_{1} un rayo de luz deja el chorro del punto A y otro rayo sale a la vez t2=t1+δ δ t{displaystyle T_{2}=t_{1}+delta t} desde el punto B. Un observador en O recibe los rayos a la vez t1.. {displaystyle ¿Qué? y t2.. {displaystyle ¡No! respectivamente. El ángulo φ φ {displaystyle phi } es lo suficientemente pequeño que las dos distancias marcadas DL{displaystyle D_{L} puede considerarse igual.

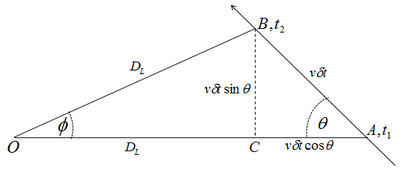
AB=vδ δ t{displaystyle AB=v,delta t}

AC=vδ δ t#⁡ ⁡ Silencio Silencio {displaystyle AC=v,delta tcos theta }

BC=vδ δ tpecado⁡ ⁡ Silencio Silencio {displaystyle BC=v,delta tsin theta }

t2− − t1=δ δ t{displaystyle T_{2}-t_{1}=delta t}

t1.=t1+DL+vδ δ t#⁡ ⁡ Silencio Silencio c{displaystyle T_{1}=t_{1}+{frac {D_{L}+v,delta tcos theta } {c}}

t2.=t2+DLc{displaystyle T_{2}=t_{2}+{frac {fnK}} {}}} {c}}} {c}}}} {c}}}} {c}}}}}} {c}}}} {c}}}}} {c}}}}}}}}}}} {c}}}}}}}} {c}}}}}}}}}}}}}}}}}} {}}}}} {}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

δ δ t.=t2.− − t1.=t2− − t1− − vδ δ t#⁡ ⁡ Silencio Silencio c=δ δ t− − vδ δ t#⁡ ⁡ Silencio Silencio c=δ δ t()1− − β β #⁡ ⁡ Silencio Silencio ){displaystyle delta t'=t_{2}-t_{1}'=t_{2}-t_{1}-{frac {v,delta tcos theta } {c}=delta t-{frac {v,delta tcos theta } {c}=delta t(1-beta cos theta)}, donde β β =v/c{displaystyle beta =v/c}

δ δ t=δ δ t.1− − β β #⁡ ⁡ Silencio Silencio {displaystyle delta t={frac {delta t'}{1-beta cos theta }

BC=DLpecado⁡ ⁡ φ φ .. φ φ DL=vδ δ tpecado⁡ ⁡ Silencio Silencio ⇒ ⇒ φ φ DL=vpecado⁡ ⁡ Silencio Silencio δ δ t.1− − β β #⁡ ⁡ Silencio Silencio {displaystyle BC=D_{L}sin phi approx phi D_{L}=v,delta tsin theta Rightarrow phi D_{L}=vsin theta {frac {delta t'}{1-beta cos theta }

Velocidad transversa aparente CB{displaystyle CB., vT=φ φ DLδ δ t.=vpecado⁡ ⁡ Silencio Silencio 1− − β β #⁡ ⁡ Silencio Silencio {displaystyle ¿Qué? {fnfnfnfnh} {fnfnfns}{1-beta cos theta }

β β T=vTc=β β pecado⁡ ⁡ Silencio Silencio 1− − β β #⁡ ⁡ Silencio Silencio .{displaystyle beta _{text{T}={frac {fnK} {fnMicroc}} {fnMicroc}} {fnK}} {f}}} {f}}} {fn}}} {fn}}}} {fnK}}}}} {f}} {fnf}}} {fnKf}}} {f}f}}}}f}}}}}}}}}}}}}}}\\fn\\fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnMicroc}fnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnfnf}}}}}}}}}}}}} {beta sin theta }{1-beta cos theta }}

La velocidad aparente transversal es máxima para ángulo (<math alttext="{displaystyle 0<beta 0.β β .1{displaystyle 0.<img alt="{displaystyle 0<beta se utiliza)

∂ ∂ β β T∂ ∂ Silencio Silencio =∂ ∂ ∂ ∂ Silencio Silencio [β β pecado⁡ ⁡ Silencio Silencio 1− − β β #⁡ ⁡ Silencio Silencio ]=β β #⁡ ⁡ Silencio Silencio 1− − β β #⁡ ⁡ Silencio Silencio − − ()β β pecado⁡ ⁡ Silencio Silencio )2()1− − β β #⁡ ⁡ Silencio Silencio )2=0{displaystyle {frac {partial beta {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} theta }={frac {partial }{partial theta }left[{frac {beta sin theta }{1-beta cos theta {beta cos theta}{1-beta cos theta }-{frac {betasin theta)}{2}{(1-beta cos theta)^{2}}=0}

⇒ ⇒ β β #⁡ ⁡ Silencio Silencio ()1− − β β #⁡ ⁡ Silencio Silencio )2=()1− − β β #⁡ ⁡ Silencio Silencio )()β β pecado⁡ ⁡ Silencio Silencio )2{displaystyle Rightarrow beta cos theta (1-beta cos theta)^{2}=(1-beta cos theta)(beta sin theta)^{2}}

⇒ ⇒ β β #⁡ ⁡ Silencio Silencio ()1− − β β #⁡ ⁡ Silencio Silencio )=()β β pecado⁡ ⁡ Silencio Silencio )2⇒ ⇒ β β #⁡ ⁡ Silencio Silencio − − β β 2#2⁡ ⁡ Silencio Silencio =β β 2pecado2⁡ ⁡ Silencio Silencio ⇒ ⇒ #⁡ ⁡ Silencio Silencio max=β β {displaystyle Rightarrow beta cos theta (1-beta cos theta)=(beta sin theta)^{2}Rightarrow beta cos theta -beta ^{2}cos ^{2}theta =beta ^{2}sin ^{2}theta Rightarrow cos theta _{text{max}=beta }

⇒ ⇒ pecado⁡ ⁡ Silencio Silencio max=1− − #2⁡ ⁡ Silencio Silencio max=1− − β β 2=1γ γ {displaystyle Rightarrow sin theta _{text{max}={sqrt {1-cos ^{2}theta _{text{max}}={sqrt {1-beta ^{2}={frac} {1}{gamma },}, donde γ γ =11− − β β 2{displaystyle gamma ={frac {1}{sqrt {1-beta ^{2}}}

▪ ▪ β β Tmax=β β pecado⁡ ⁡ Silencio Silencio max1− − β β #⁡ ⁡ Silencio Silencio max=β β /γ γ 1− − β β 2=β β γ γ {displaystyle therefore beta _{text{T}{text{max}={frac} {betasin theta _{text{max}}{1-beta cos theta - ¿Qué? {beta}=beta gamma

Si γ γ ≫ ≫ 1{displaystyle gamma gg 1} (es decir, cuando la velocidad del jet está cerca de la velocidad de la luz) entonces 1}" xmlns="http://www.w3.org/1998/Math/MathML">β β Tmax■1{displaystyle beta _{text{T}}} {text{max}}]}}} {f}}}}1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fdcfde6f77c73fa0be43c84b18188e7c7d7e7986" style="vertical-align: -1.005ex; width:8.889ex; height:2.843ex;"/> a pesar de que <math alttext="{displaystyle beta β β .1{displaystyle beta.<img alt="beta . Y por supuesto 1}" xmlns="http://www.w3.org/1998/Math/MathML">β β T■1{displaystyle beta _{text{T} {}}}]1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/33d706a313adf8e67d15d451821626ff4889c804" style="vertical-align: -0.671ex; width:6.995ex; height:2.509ex;"/> significa que la velocidad transversal aparente CB{displaystyle CB., la única velocidad en el cielo que se puede medir, es mayor que la velocidad de la luz en vacío, es decir, el movimiento es aparentemente superluminal.

Historia

El aparente movimiento superluminal en la tenue nebulosa que rodea a Nova Persei fue observado por primera vez en 1901 por Charles Dillon Perrine. "Señor. La fotografía de Perrine del 7 y 8 de noviembre de 1901, obtenida con el reflector Crossley, condujo al notable descubrimiento de que las masas de nebulosidad aparentemente estaban en movimiento, con una velocidad quizás varios cientos de veces mayor que la observada hasta ahora. “Usando el modelo de 36 pulgadas. Telescopio (Crossley), descubrió el aparente movimiento superluminal de la burbuja de luz en expansión alrededor de Nova Persei (1901). Se pensaba que era una nebulosa, pero la apariencia visual en realidad fue causada por la luz del evento de nova reflejada desde el medio interestelar circundante a medida que la luz se alejaba de la estrella. Perrine estudió este fenómeno utilizando técnicas fotográficas, espectroscópicas y de polarización”.

El movimiento superluminal fue observado por primera vez en 1902 por Jacobus Kapteyn en la eyección de la nova GK Persei, que había explotado en 1901. Su descubrimiento fue publicado en la revista alemana Astronomische Nachrichten y recibió poca atención. desde los astrónomos de habla inglesa hasta muchas décadas después.

En 1966, Martin Rees señaló que "un objeto que se mueve relativistamente en direcciones adecuadas puede parecerle a un observador distante que tiene una velocidad transversal mucho mayor que la velocidad de la luz". En 1969 y 1970 se encontraron fuentes de radio astronómicas muy distantes, como radiogalaxias y cuásares, y se las llamó fuentes superluminales. El descubrimiento fue el resultado de una nueva técnica llamada interferometría de línea de base muy larga, que permitió a los astrónomos establecer límites al tamaño angular de los componentes y determinar posiciones en mejor que milisegundos de arco y, en particular, determinar el cambio de posiciones en el cielo., llamados movimientos propios, en un lapso de tiempo típicamente de años. La velocidad aparente se obtiene multiplicando el movimiento propio observado por la distancia, que podría ser hasta 6 veces la velocidad de la luz.

En la introducción a un taller sobre fuentes de radio superluminales, Pearson y Zensus informaron

Los primeros indicios de cambios en la estructura de algunas fuentes fueron obtenidos por un equipo americano-Australiano en una serie de observaciones transpacíficas de VLBI entre 1968 y 1970 (Gubbay et al. 1969). Tras los primeros experimentos, habían realizado el potencial de las antenas de rastreo de la NASA para mediciones de VLBI y habían establecido un interferómetro que operaba entre California y Australia. El cambio en la visibilidad de la fuente que midieron para 3C 279, combinado con cambios en la densidad total del flujo, indicó que un componente visto por primera vez en 1969 había alcanzado un diámetro de aproximadamente 1 milarcsecond, lo que implica una expansión a una velocidad aparente de al menos dos veces la velocidad de la luz. Consciente del modelo de Rees (Moffet et al. 1972) concluyó que su medición presentaba pruebas para la expansión relativista de este componente. Esta interpretación, aunque de ninguna manera única, fue confirmada posteriormente, y en retrospectiva parece justo decir que su experimento fue la primera medición interferométrica de la expansión superluminal.

En 1994, se obtuvo un récord de velocidad galáctica con el descubrimiento de una fuente superluminal en la Vía Láctea, la fuente cósmica de rayos X GRS 1915+105. La expansión se produjo en un plazo mucho más corto. Se observó que varias manchas separadas se expandían en pares en unas semanas, normalmente 0,5 segundos de arco. Debido a la analogía con los cuásares, esta fuente se llamó microcuásar.