Movimiento propio

Hace un año el objeto era d unidades de distancia del Sol, y su luz se movió en un año por ángulo μ radian/s. Si no ha habido distorsión por lentes gravitacionales o de otro modo μ = vtd{fnMicroc} {fn} {}} {}}} {fn}}} {f}}}} {f}}}}}}} {f}}}}}}}} {f}}}}}}} {f}}} {f}}}} {}}}}}}}} {}}}}}}}} {}}}}}}}}}} {}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} Donde vt{displaystyle V_{t} es la distancia (generalmente expresada como velocidad anual) transversal (tangencial o perpendicular) a la línea de visión del Sol. El ángulo es azul claro sombreado desde el sol hasta el punto de inicio del objeto y su posición posterior año como si no tuviera velocidad radial.
En este diagrama la velocidad radial pasa a ser uno del sol y la separación del objeto, así que es positiva.
El movimiento propio es la medida astrométrica de los cambios observados en los lugares aparentes de las estrellas u otros objetos celestes en el cielo, vistos desde el centro de masa del Sistema Solar, en comparación con el resumen fondo de las estrellas más lejanas.
Los componentes para el movimiento propio en el sistema de coordenadas ecuatoriales (de una época dada, a menudo J2000.0) se dan en la dirección de ascensión recta (μα) y de declinación (μδ). Su valor combinado se calcula como el movimiento propio total (μ). Tiene dimensiones de ángulo por tiempo, típicamente segundos de arco por año o milisegundos de arco por año.
El conocimiento del movimiento, la distancia y la velocidad radial adecuados permite calcular el movimiento de un objeto desde el marco de referencia de nuestro sistema estelar y su movimiento desde el marco de referencia galáctico, es decir, movimiento con respecto al Sol, y por transformación de coordenadas, la respecto a la Vía Láctea.
Introducción
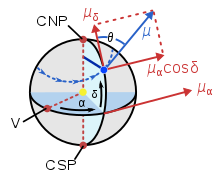
En rojo el diagrama añade los componentes del movimiento adecuado a través de la esfera celestial.
Un momento ideal para medir exactamente un pequeño cambio anual está en culminación. La culminación de la estrella se alcanza diariamente cuando el observador (y la tierra) pasa como se muestra por las flechas azules "debajo" la estrella.
Los ejes positivos de los dos componentes de su cambio generalmente anual medido o publicado en movimiento adecuado son las flechas rojas exageradas, nota: las flechas derechas apuntan al horizonte este. Una anotación roja es subtly más corta ya que la cosina de una estrella descansando a 0° declinación es 1, por lo que el cambio este o oeste de una estrella no tendría que ser multiplicado por la cosina de su declinación.
El vector de movimiento adecuado es μ, α = ascensión derecha, δ = declinación, Silencio = ángulo de posición.
A lo largo de los siglos, las estrellas parecen mantener posiciones casi fijas entre sí, de modo que forman las mismas constelaciones a lo largo del tiempo histórico. Ursa Major o Crux, por ejemplo, se ven casi iguales ahora que hace cientos de años. Sin embargo, observaciones precisas a largo plazo muestran que las constelaciones cambian de forma, aunque muy lentamente, y que cada estrella tiene un movimiento independiente.
Este movimiento es causado por el movimiento de las estrellas en relación con el Sol y el Sistema Solar. El Sol viaja en una órbita casi circular (el círculo solar) alrededor del centro de la galaxia a una velocidad de aproximadamente 220 km/s en un radio de 8000 parsecs (26 000 ly) desde Sagitario A*, que puede tomarse como la tasa de rotación de la propia Vía Láctea en este radio.
Todo movimiento propio es un vector bidimensional (ya que excluye la componente en cuanto a la dirección de la línea de visión) y tiene dos cantidades o características: su ángulo de posición y su magnitud. El primero es la dirección del movimiento propio en la esfera celeste (0 grados significa que el movimiento es hacia el norte, 90 grados significa que el movimiento es hacia el este, (a la izquierda en la mayoría de los mapas del cielo e imágenes de telescopios espaciales) y así sucesivamente), y el segundo es su magnitud, normalmente expresada en segundos de arco por año (símbolos: arcsec/yr, as/yr, ″/yr, ″ yr−1) o miliarcosegundos por año (símbolos: mas/yr, mas yr −1).
El movimiento propio puede definirse alternativamente por los cambios angulares por año en la ascensión recta de la estrella (μα) y la declinación (μδ) con respecto a una época constante.
Los componentes del movimiento propio por convención se obtienen de la siguiente manera. Supongamos que un objeto se mueve de las coordenadas (α1, δ1) a las coordenadas (α2, δ2) en un tiempo Δt. Los movimientos propios vienen dados por:
- μ μ α α =α α 2− − α α 1Δ Δ t,{displaystyle mu _{alpha }={frac {alpha ¿Qué? ¿Qué? Delta,
- μ μ δ δ =δ δ 2− − δ δ 1Δ Δ t.{displaystyle mu _{delta }={frac {delta _{2}-delta ¿Qué? Delta.
La magnitud del movimiento propio μ viene dada por el teorema de Pitágoras:
- μ μ 2=μ μ δ δ 2+μ μ α α 2⋅ ⋅ #2 δ δ ,{displaystyle mu ^{2}={mu _{delta }{2}+{mu _{alpha } {2}cdot cos ^{2}delta }
- técnicamente abreviado:
- μ μ 2=μ μ δ δ 2+μ μ α α Alternativa Alternativa 2.{displaystyle mu ^{2}={mu _{delta }{2}+{mu ¿Qué?
donde δ es la declinación. El factor en cos2δ explica el ensanchamiento de las líneas (horas) de ascensión recta alejándose de los polos, cosδ, siendo cero para un objeto hipotético fijo en un polo celeste en declinación. Por lo tanto, se da un coeficiente para negar la engañosamente mayor velocidad este u oeste (cambio angular en α) en horas de Ascensión Recta cuanto más lejos está hacia los polos infinitos imaginarios, por encima y por debajo de la tierra& #39;s eje de rotación, en el cielo. El cambio μα, que debe multiplicarse por cosδ para convertirse en un componente del movimiento propio, a veces se denomina " movimiento propio en ascensión recta", y μδ el "movimiento propio en declinación".
Si el movimiento propio en ascensión recta ha sido convertido por cosδ, el resultado se denomina μα*. Por ejemplo, los resultados de movimiento propio en ascensión recta en el Catálogo Hipparcos (HIP) ya se han convertido. Por lo tanto, los movimientos propios individuales en ascensión recta y declinación se hacen equivalentes para los cálculos directos de varios otros movimientos estelares.
El ángulo de posición θ está relacionado con estos componentes por:
- μ μ pecado Silencio Silencio =μ μ α α # δ δ =μ μ α α Alternativa Alternativa ,{displaystyle mu sin theta = 'mu' }cos delta =mu _{alpha ast}
- μ μ # Silencio Silencio =μ μ δ δ .{displaystyle mu cos theta =mu _{delta }
Los movimientos en coordenadas ecuatoriales se pueden convertir en movimientos en coordenadas galácticas.
Ejemplos
Para la mayoría de las estrellas que se ven en el cielo, los movimientos propios observados son pequeños y anodinos. Tales estrellas a menudo son débiles o están significativamente distantes, tienen cambios de menos de 0.01″ por año y no parecen moverse apreciablemente durante muchos milenios. Algunas sí tienen movimientos significativos, y generalmente se las llama estrellas de alto movimiento propio. Los movimientos también pueden tener direcciones aparentemente aleatorias. Dos o más estrellas, estrellas dobles o cúmulos estelares abiertos, que se mueven en direcciones similares, exhiben el llamado movimiento propio compartido o común (o cpm), lo que sugiere que pueden estar unidas gravitacionalmente o compartir movimientos similares. movimiento en el espacio.
La estrella de Barnard tiene el movimiento propio más grande de todas las estrellas, moviéndose a 10,3″ año−1. Un movimiento propio grande generalmente indica fuertemente que un objeto está cerca del Sol. Esto es así para la estrella de Barnard, a unos 6 años luz de distancia. Después del Sol y el sistema Alfa Centauro, es la estrella conocida más cercana. Al ser una enana roja con una magnitud aparente de 9,54, es demasiado débil para verla sin un telescopio o binoculares potentes. De las estrellas visibles a simple vista (limitando conservadoramente la magnitud visual sin ayuda a 6,0), 61 Cygni A (magnitud V=5,20) tiene el movimiento propio más alto a 5,281″ yr−1, descontando Groombridge 1830 (magnitud V=6,42), movimiento propio: 7,058″ yr−1.
Un movimiento propio de 1 arcsec por año a 1 año luz de distancia corresponde a una velocidad transversal relativa de 1,45 km/s. La velocidad transversal de la estrella de Barnard es de 90 km/s y su velocidad radial es de 111 km/s (perpendicular (en un ángulo recto de 90°), lo que da una verdadera o 'espacial'; movimiento de 142 km/s. El movimiento verdadero o absoluto es más difícil de medir que el movimiento propio, porque la velocidad transversal verdadera implica el producto del movimiento propio por la distancia. Como se muestra en esta fórmula, las mediciones de la velocidad verdadera dependen de la distancia mediciones, que son difíciles en general.
En 1992, Rho Aquilae se convirtió en la primera estrella a la que se le invalidó la designación de Bayer al trasladarse a una constelación vecina; ahora se encuentra en Delphinus.
Utilidad en astronomía
Las estrellas con grandes movimientos propios tienden a estar cerca; la mayoría de las estrellas están lo suficientemente lejos como para que sus movimientos propios sean muy pequeños, del orden de unas pocas milésimas de segundo de arco por año. Es posible construir muestras casi completas de estrellas de alto movimiento propio comparando imágenes fotográficas de estudios del cielo tomadas con muchos años de diferencia. El Palomar Sky Survey es una fuente de tales imágenes. En el pasado, las búsquedas de objetos con alto movimiento propio se realizaban utilizando comparadores de parpadeo para examinar las imágenes a simple vista. Las técnicas más modernas, como la diferenciación de imágenes, pueden escanear imágenes digitalizadas o comparaciones con catálogos de estrellas obtenidos por satélites. Dado que cualquier sesgo de selección de estas encuestas se comprende bien y es cuantificable, los estudios han confirmado más e inferido cantidades aproximadas de estrellas invisibles, revelando y confirmando más al estudiarlas más, independientemente del brillo, por ejemplo. Estudios de este tipo muestran que la mayoría de las estrellas más cercanas son intrínsecamente débiles y angularmente pequeñas, como las enanas rojas.
La medición de los movimientos propios de una gran muestra de estrellas en un sistema estelar distante, como un cúmulo globular, se puede utilizar para calcular la masa total del cúmulo mediante el estimador de masa Leonard-Merritt. Junto con las medidas de las estrellas' velocidades radiales, los movimientos propios se pueden utilizar para calcular la distancia al cúmulo.
Se han utilizado movimientos propios estelares para inferir la presencia de un agujero negro supermasivo en el centro de la Vía Láctea. Se sospecha que este agujero negro es Sgr A*, con una masa de 4,2 × 106 M☉ (masas solares).
Los movimientos propios de las galaxias en el Grupo Local se discuten en detalle en Röser. En 2005, se realizó la primera medición del movimiento propio de Triangulum Galaxy M33, la tercera galaxia espiral ordinaria más grande y única del Grupo Local, ubicada 0,860 ± 0,028 Mpc más allá de la Vía Láctea. El movimiento de la galaxia de Andrómeda se midió en 2012, y se prevé una colisión entre Andrómeda y la Vía Láctea en unos 4500 millones de años. El movimiento propio de la galaxia NGC 4258 (M106) en el grupo de galaxias M106 se utilizó en 1999 para encontrar una distancia precisa a este objeto. Se realizaron mediciones del movimiento radial de los objetos en esa galaxia moviéndose directamente hacia nosotros y alejándose de nosotros, y asumiendo que este mismo movimiento se aplica a objetos con solo un movimiento propio, el movimiento propio observado predice una distancia a la galaxia de 7.2±0.5 Mpc .
Historia
Los primeros astrónomos sospecharon el movimiento propio (según Macrobius, 400 d. C.), pero Edmund Halley no proporcionó una prueba hasta 1718, quien notó que Sirius, Arcturus y Aldebaran estaban a más de medio grado de distancia de las posiciones cartografiadas por el el antiguo astrónomo griego Hipparchus aproximadamente 1850 años antes.
El significado menor de "apropiado" podría decirse que es un inglés fechado (pero ni histórico ni obsoleto cuando se usa como postpositivo, como en "la ciudad propiamente dicha") que significa "perteneciente a" o "propio". "Movimiento incorrecto" se referiría al movimiento percibido que no tiene nada que ver con el curso inherente de un objeto, como el debido a la precesión axial de la tierra y desviaciones menores, nutaciones dentro del ciclo de 26,000 años.
Estrellas con alto movimiento propio
Las siguientes son las estrellas con mayor movimiento propio del catálogo Hipparcos. No incluye estrellas como la estrella de Teegarden, que son demasiado débiles para ese catálogo. Se puede hacer una lista más completa de objetos estelares haciendo una consulta de criterio en la base de datos astronómica SIMBAD.
| # | Star | moción adecuada | Radial velocidad (km/s) | Parallax (Segundos de arco) | Distancia en parsecs ()1parallax){displaystyle left({frac {1}{text{parallax}}right)} | |
|---|---|---|---|---|---|---|
| μα · porque δ (mas/yr) | μδ (mas/yr) | |||||
| 1 | La estrella de Barnard | −798.58 | 10328.12 | 110−51 | 0,4831 | 1.82 |
| 2 | La estrella de Kapteyn | 6505.08 | −5730.84 | +245.19 | 0.25566 | 3.91 |
| 3 | Groombridge 1830 | 4003.98 | −58-13.62 | 98−35 | 0.10999 | 9.09 |
| 4 | Lacaille 9352 | 6768.20 | 1327.52 | +8.81 | 0.30526 | 3.28 |
| 5 | Gliese 1 (CD - 37 15492) (GJ 1) | 5634.68 | 23 a 37,71 | +25.38 | 0.23042 | 4.34 |
| 6 | HIP 67593 | 2118.73 | 5397.57 | -4.4 | 0.18776 | 5.33 |
| 7 | 61 Cygni A " B " | 4133.05 | 3201.78 | 65 a 74 | 0,286 | 3.50 |
| 8 | Lalande 21185 | 5 a 80,27 | −4765,85 | 84−69 | 0,9264 | 2.55 |
| 9 | Epsilon Indi | 3960.93 | −25−39.23 | −40.00 | 0.27606 | 3.62 |
La cifra de HIP 67593 es casi seguro un error, probablemente porque la estrella tiene un compañero binario visual más brillante relativamente cercano; el movimiento entre las imágenes DSS2 y SDSS9 es menor. Gaia midió un movimiento propio mucho más pequeño para su Data Release 2, pero un paralaje de 15 veces entre él y su probable compañero de movimiento propio común HIP 67594. La reconciliación de su distancia y movimiento tendrá que esperar a que Data Release 3 se analice bien. Objetos de muy alto movimiento propio.
Contenido relacionado
Deimos (luna)
Luminosidad
Betelgeuse










