Movimiento hiperbólico (relatividad)

Movimiento hiperbólico es el movimiento de un objeto con constante aceleración adecuada en la relatividad especial. Se llama movimiento hiperbólico porque la ecuación que describe el camino del objeto a través del espacio es un hiperbola, como se puede ver cuando se grafica en un diagrama de Minkowski cuyas coordenadas representan un marco inercial adecuado (no acelerado). Esta moción tiene varias características interesantes, entre ellas que es posible superar un fotón si se le da un inicio de cabeza suficiente, como se puede concluir desde el diagrama.

Historia

Hermann Minkowski (1908) demostró la relación entre un punto en una línea de mundo y la magnitud de una aceleración de cuatro y una "hipérbola de curvatura" (Alemán: Krümmungshyperbel). En el contexto de la rigidez de Born, Max Born (1909) acuñó posteriormente el término "movimiento hiperbólico" (movimiento hiperbólico). (alemán: Hyperbelbewegung) para el caso de magnitud constante de cuatro aceleraciones, luego proporcionó una descripción detallada de las partículas cargadas en movimiento hiperbólico e introdujo la correspondiente "aceleración hiperbólica sistema de referencia" (Alemán: hyperbolisch beschleunigtes Bezugsystem). Las fórmulas de Born fueron simplificadas y ampliadas por Arnold Sommerfeld (1910). Para reseñas anteriores, consulte los libros de texto de Max von Laue (1911, 1921) o Wolfgang Pauli (1921). Véase también Galeriu (2015) o Gourgoulhon (2013), y Aceleración (relatividad especial)#Historia.

Línea mundial

La aceleración adecuada α α {displaystyle alpha } de una partícula se define como la aceleración que una partícula "sentirá" a medida que se acelera de un marco de referencia inercial a otro. Si la aceleración adecuada se dirige paralelamente a la línea de movimiento, se relaciona con la tres aceleración ordinaria en la relatividad especial a=du/dT{displaystyle a=du/dT} por

α α =γ γ 3a=1()1− − u2/c2)3/2dudT,{displaystyle alpha =gamma ¿Qué?

Donde u{displaystyle u} es la velocidad instantánea de la partícula, γ γ {displaystyle gamma } el factor Lorentz, c{displaystyle c} es la velocidad de la luz, y T{displaystyle T} es el tiempo de coordenadas. Resolver la ecuación del movimiento da las fórmulas deseadas, que se pueden expresar en términos de tiempo de coordinación T{displaystyle T} así como tiempo adecuado τ τ {displaystyle tau }. Para simplificación, todos los valores iniciales para el tiempo, ubicación y velocidad se pueden establecer a 0, por lo tanto:

u()T)=α α T1+()α α Tc)2=cTanh⁡ ⁡ ()arsinh⁡ ⁡ α α Tc)X()T)=c2α α ()1+()α α Tc)2− − 1)=c2α α ()cosh⁡ ⁡ ()arsinh⁡ ⁡ α α Tc)− − 1)cτ τ ()T)=c2α α In⁡ ⁡ ()1+()α α Tc)2+α α Tc)=c2α α arsinh⁡ ⁡ α α Tcu()τ τ )=cTanh⁡ ⁡ α α τ τ cX()τ τ )=c2α α ()cosh⁡ ⁡ α α τ τ c− − 1)cT()τ τ )=c2α α pecado⁡ ⁡ α α τ τ c{displaystyle {begin{rray}{begin{aligned}u(T) sensible={frac {fnMicrosoft} {fnMicrosoft {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f} {fnMicrosoft} {fnMicrosoft} {f}} {f} {f} {fnMicrosoft}} {f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f} {f}f}f}f}f}sqsqsqsqsqsqf}sqsqsqsqsqsq\sqsqsqsqsqsqsqsqsqsqsqs {fnMicrosoft Sans Serif}}}\\cctanh left(operatorname {arsinh} {frac {alpha {c}{c}}c}ccc}ccccccccc}left({sqrt {1+left({frac {alpha ################################################################################################################################################################################################################################################################ T} {c}right)-1ctau (T) Condenado={frac {c^{2}{alpha }ln left({sqrt {1+left({frac {alpha {fnMicrosoft Sans Serif}fnMicroc {c}c}right)\fnMicroc {c}{2}{alpha # Operadorname {arsinh} {frac {alpha T} {c}end{aligned} {begin{aligned}u(tau) {fnMicroc {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc} {fnMicroc}}}}}}}\\fnun}\\\\fnMish {fnMish {fnMish {fnMish {fnMish {fnMish {fnMish {fnKfnKfnMicroc}fnKfnK}fnKfnMish {fnMish {fnK}fnMicroc}fnMicroc}fnMicroc}}}fnMicroc}}}\fnMicroc}fnMicroc}}}fn {alpha tau {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {c} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif}} {fnMicrosoft Sans Serif} }peh {frac {alpha tau {}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\

()1)

Esto da ()X+c2/α α )2− − c2T2=c4/α α 2{displaystyle left(X+c^{2}/alpha right)}{2}-c^{2}=c^{4}/alpha ^{2}}, que es una hiperbola en el tiempo T y la variable de ubicación espacial X{displaystyle X}. En este caso, el objeto acelerado se encuentra en X=0{displaystyle X=0} a la vez T=0{displaystyle T=0}. Si en cambio hay valores iniciales diferentes de cero, las fórmulas para el movimiento hiperbólico asumen la forma:

u()T)=u0γ γ 0+α α T1+()u0γ γ 0+α α Tc)2=cTanh⁡ ⁡ {}arsinh⁡ ⁡ ()u0γ γ 0+α α Tc)}X()T)=X0+c2α α ()1+()u0γ γ 0+α α Tc)2− − γ γ 0)=X0+c2α α {}cosh⁡ ⁡ [arsinh⁡ ⁡ ()u0γ γ 0+α α Tc)]− − γ γ 0}cτ τ ()T)=cτ τ 0+c2α α In⁡ ⁡ ()c2+()u0γ γ 0+α α T)2+u0γ γ 0+α α T()c+u0)γ γ 0)=cτ τ 0+c2α α {}arsinh⁡ ⁡ ()u0γ γ 0+α α Tc)− − Artanh⁡ ⁡ ()u0c)}u()τ τ )=cTanh⁡ ⁡ {}Artanh⁡ ⁡ ()u0c)+α α τ τ c}X()τ τ )=X0+c2α α {}cosh⁡ ⁡ [Artanh⁡ ⁡ ()u0c)+α α τ τ c]− − γ γ 0}cT()τ τ )=cT0+c2α α {}pecado⁡ ⁡ [Artanh⁡ ⁡ ()u0c)+α α τ τ c]− − u0γ γ 0c}{displaystyle {scriptstyle {begin{array}{c habitc}{begin{aligned}u(T) limit={frac {u_{0}gamma ################################################################################################################################################################################################################################################################ {fnMicrosoft Sans Serif}}}quad\cctanh left{operatorname {arsinh} left({frac {u_{0}gamma _{0}+alpha {fnMicrosoft Sans Serif}x(T)}=X_{0}+{frac {c^{2}{alpha }}left({sqrt {1+left({frac {u_{0}gamma _{0}+alpha ¿Qué? ¿Por qué? }left{cosh left[operatorname {arsinh} left({frac {u_{0}gamma _{0}+alpha T}{c}right)right]-gamma ¿Por qué? }ln left({frac {sqrt {c^{2}+left(u_{0}gamma ¿Por qué? ¿Por qué? ¿Por qué? {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} }left{fnK} left({frac {u_{0}gamma _{0}+alpha ¿Qué? left{operatorname {artanh} left({frac {u_{0} {c}right)+{frac} {alpha tau ################################################################################################################################################################################################################################################################ }left{cosh left[operatorname {artanh} left({frac {u_{0} {c}right)+{frac} {alpha tau} {}derecha]-gamma ¿Por qué? }leftpeh left[operatorname {artanh} left({frac {u_{0} {c}right)+{frac} {Alpha tau} {c}derecha]-{frac {u_{0}gamma {fnK} {fnK}} {fnK}} {fnK}}}} {fnK}}}} {f}}}}}}}} {fnK}} {fnK}}}}}} {f}} {f}}} {f}}} {f}}}}}}}}}}}}}}}}}}}}f}}}}}}}}}}}}}}}}}}}}}}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} {

Rapidez

La línea mundial para el movimiento hiperbólico (que de ahora en adelante se escribirá como una función del tiempo propio) se puede simplificar de varias maneras. Por ejemplo, la expresión

X=c2α α ()cosh⁡ ⁡ α α τ τ c− − 1){displaystyle X={2}{alpha }left(cosh {frac {alpha tau}{c}}}right)}

puede ser sometido a un cambio espacial de la cantidad c2/α α {displaystyle c^{2}/alpha, así

X=c2α α cosh⁡ ⁡ α α τ τ c{displaystyle X={f} {f} {fnMicrosoft} {fnMicrosoft} {f}} {f}}}} {f}}}} {fnMicrosoft}}} {f}}}}} {f}} . {alpha tau } {c}},

por el cual el observador está en posición X=c2/α α {displaystyle X=c^{2}/alpha } a la vez T=0{displaystyle T=0}. Además, estableciendo x=c2/α α {displaystyle x=c^{2}/alpha } e introducción de la rapidez . . =Artanh⁡ ⁡ uc=α α τ τ c{displaystyle eta =operatorname {artanh} {fnMicroc {u} {c}={frac} {alpha tau } {c}}, las ecuaciones para movimiento hiperbólico reducen a

cT=xpecado⁡ ⁡ . . ,X=xcosh⁡ ⁡ . . {displaystyle cT=xsinh etaquad X=xcosh eta }

()2)

con el hiperbola X2− − c2T2=x2{displaystyle ¿Qué?.

Partículas cargadas en movimiento hiperbólico

Nacido (1909), Sommerfeld (1910), von Laue (1911), Pauli (1921) también formuló las ecuaciones para el campo electromagnético de partículas cargadas en movimiento hiperbólico. Esto fue ampliado por Hermann Bondi " Thomas Gold (1955) y Fulton " Rohrlich (1960)

E*** *** ..=()8e/α α 2)*** *** .z.. . . . 3Ez..=− − ()4e/α α 2)1/α α 2+t. . 2+*** *** . . 2− − z. . 2. . . . 3Eφ φ ..=Hφ φ ..=Hz..=0Hφ φ ..=()8e/α α 2)*** *** .t.. . . . 3. . .=()1/α α 2+t. . 2− − *** *** . . 2− − z. . 2)2+()2*** *** ./α α )2{displaystyle {begin{aligned}E_{rho '}'= âfrac {left(8e/alpha ^{2}right)rho 'z'}{xi ^{prime 3}}E_{z'}'= limitada{frac {-left(4e/alpha ^{2}right)1/alpha ^{2}+t^{prime 2}+rho ^{prime 2}-z^{prime 2}}}{xi ^{prime {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicroc {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {cfnMicrosoft Sans}fnMicros}f}\fnMis}fnMicros}s}fnK}fnMis}\fnMicros}\\\fnMicros}\\\s}s\\\\\\\\\\\\\\\\\\\fnK\fnK\\\\\\\\\\\\\\\\\\\\\\fnMin ¿Qué?

Esto está relacionado con la controvertida cuestión de si las cargas en movimiento hiperbólico perpetuo irradian o no, y si esto es consistente con el principio de equivalencia, aunque se trata de una situación ideal, porque el movimiento hiperbólico perpetuo es imposible. Mientras que los primeros autores como Born (1909) o Pauli (1921) sostuvieron que no surge radiación, autores posteriores como Bondi & Oro y Fulton &Amp; Rohrlich demostró que efectivamente existe radiación.

Marco de referencia adecuado

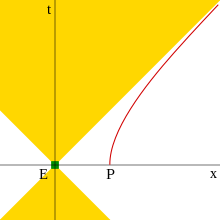
En la ecuación2) para el movimiento hiperbólico, la expresión x{displaystyle x} era constante, mientras que la rapidez . . {displaystyle eta } era variable. Sin embargo, como señaló Sommerfeld, se puede definir x{displaystyle x} como variable, mientras que . . {displaystyle eta } constante. Esto significa que las ecuaciones se convierten en transformaciones que indican la forma de reposo simultáneo de un cuerpo acelerado con coordenadas hiperbólicas ()x,Sí.,z,. . ){displaystyle (x,y,z,eta)} as seen by a comoving observer

cT=xpecado⁡ ⁡ . . ,X=xcosh⁡ ⁡ . . ,Y=Sí.,Z=z{displaystyle cT=xsinh etaquad X=xcosh etaquad Y=y,quad Z=z}

Mediante esta transformación, el tiempo propio pasa a ser el tiempo del cuadro hiperbólicamente acelerado. Estas coordenadas, que comúnmente se denominan coordenadas de Rindler (variantes similares se denominan coordenadas de Kottler-Møller o coordenadas de Lass), pueden verse como un caso especial de las coordenadas de Fermi o coordenadas adecuadas, y a menudo se utilizan en relación con el efecto Unruh. Utilizando estas coordenadas, resulta que los observadores en movimiento hiperbólico poseen un horizonte de sucesos aparente, más allá del cual ninguna señal puede alcanzarlos.

Transformación conforme especial

Un método menos conocido para definir un sistema de referencia en movimiento hiperbólico es el empleo de la transformación conforme especial, que consiste en una inversión, una traslación y otra inversión. Comúnmente se interpreta como una transformación de calibre en el espacio de Minkowski, aunque algunos autores la utilizan alternativamente como una transformación de aceleración (ver Kastrup para un estudio histórico crítico). Tiene la forma

Xμ μ =xμ μ − − aμ μ x21− − 2ax+a2x2{displaystyle X^{mu}={frac} {cH00FF} {cH00} {cH00cH00cH00} {cH00} {cH00\cH00\\cH00cH00\cH00cH00\cH00\cH00\cH00\\cH00cH00\\cH00\\\\\cH00\cH00cH00cH00\\cH00cH00cH00\cH00cH00cH00\\cH00\\\\\\cH00\\\\\\cH00\\cH00\cH00\\cH00\cH00cH00\\cH00\\cH00\\cH00\\cH00 }-a^{mu ¿Qué?

Usando sólo una dimensión espacial xμ μ =()t,x){displaystyle x^{mu }=(t,x)}, y simplificación adicional estableciendo x=0{displaystyle x=0}, y utilizando la aceleración aμ μ =()0,− − α α /2){displaystyle a^{mu }=(0,-alpha /2)}, sigue

T=t1− − 14α α 2t2,X=− − α α t22()1− − 14α α 2t2){displaystyle T={frac {T}{1-{frac} {1}{4}Alpha {} {2}t^{2}}}}quad X={frac {-alpha {2}{2}{2left(1-{frac {1}{4}alpha {}} {2}t^{2}}}}}

con el hiperbola ()X− − 1/α α )2− − T2=1/α α 2{displaystyle left(X-1/alpha right)^{2}-T^{2}=1/alpha ^{2}. Resulta que t=± ± ()x+2/α α ){displaystyle t=pm (x+2/alpha)} el tiempo se hace singular, a lo que Fulton & Rohrlich & Witten señala que uno tiene que mantenerse alejado de este límite, mientras que Kastrup (que es muy crítico de la interpretación de aceleración) comenta que éste es uno de los resultados extraños de esta interpretación.