Movimiento de proyectiles

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Moción de objetos lanzados debido a la gravedad

Trayectoria de movimiento de agua parabólica

moción proyectil es una forma de movimiento experimentada por un objeto o partícula (un proyectil) que se proyecta en un campo gravitatorio, como desde la superficie de la Tierra, y se mueve a lo largo de un camino curvado bajo la acción de la gravedad solamente. En el caso particular del movimiento proyectil en la Tierra, la mayoría de los cálculos suponen que los efectos de la resistencia del aire son pasivos y insignificantes. El camino curvado de los objetos en movimiento proyectil fue demostrado por Galileo para ser una parabola, pero también puede ser una línea recta en el caso especial cuando se lanza directamente hacia arriba o hacia abajo. El estudio de tales movimientos se llama balística, y tal trayectoria es una trayectoria balística. La única fuerza de significado matemático que se ejerce activamente en el objeto es la gravedad, que actúa hacia abajo, impartiendo así al objeto una aceleración hacia el centro de masa de la Tierra. Debido a la inercia del objeto, no se necesita fuerza externa para mantener el componente de velocidad horizontal del movimiento del objeto. Teniendo en cuenta otras fuerzas, como la arrastre aerodinámica o la propulsión interna (como en un cohete), se necesita un análisis adicional. Un misil balístico es un misil guiado sólo durante la fase inicial relativamente breve de vuelo, y cuyo curso restante se rige por las leyes de la mecánica clásica.

Balística (del griego antiguo βάλλειν bállein 'lanzar') es la ciencia de la dinámica que se ocupa del vuelo, comportamiento y efectos de los proyectiles, especialmente balas, bombas no guiadas, cohetes o similares; La ciencia o el arte de diseñar y acelerar proyectiles para lograr un rendimiento deseado.

La ecuación elemental de las balísticas descuida casi todos los factores excepto la velocidad inicial y una aceleración gravitacional constante asumida. Las soluciones prácticas de un problema balístico a menudo requieren consideraciones de resistencia al aire, vientos cruzados, movimiento objetivo, aceleración variable debido a la gravedad, y en problemas como lanzar un cohete desde un punto en la Tierra a otro, la rotación de la Tierra. Las soluciones matemáticas detalladas de los problemas prácticos normalmente no tienen soluciones de forma cerrada, por lo que requieren métodos numéricos para abordar.

Cantidades cinemáticas

En el movimiento de proyectil, el movimiento horizontal y el movimiento vertical son independientes entre sí; es decir, ningún movimiento afecta al otro. Este es el principio del movimiento compuesto establecido por Galileo en 1638 y utilizado por él para demostrar la forma parabólica del movimiento de un proyectil.

Una trayectoria balística es una parábola con aceleración homogénea, como en una nave espacial con aceleración constante en ausencia de otras fuerzas. En la Tierra la aceleración cambia de magnitud con la altitud y de dirección con la latitud/longitud. Esto provoca una trayectoria elíptica, que se acerca mucho a una parábola a pequeña escala. Sin embargo, si se lanzara un objeto y la Tierra fuera reemplazada repentinamente por un agujero negro de igual masa, resultaría obvio que la trayectoria balística es parte de una órbita elíptica alrededor de ese agujero negro, y no una parábola que se extiende hasta el infinito. A velocidades más altas, la trayectoria también puede ser circular, parabólica o hiperbólica (a menos que esté distorsionada por otros objetos como la Luna o el Sol). En este artículo se supone una aceleración homogénea.

Aceleración

Puesto que hay aceleración sólo en la dirección vertical, la velocidad en la dirección horizontal es constante, siendo igual a ${displaystyle mathbf {v} _{0}cos theta }$ . El movimiento vertical del proyectil es el movimiento de una partícula durante su caída libre. Aquí la aceleración es constante, siendo igual a g. Los componentes de la aceleración son:

{displaystyle a_{x}=0}

{displaystyle a_{y}=-g}

. *

*La aceleración y también puede denominarse la fuerza de la Tierra sobre el objeto(s) de interés.

Velocidad

Que el proyectil sea lanzado con una velocidad inicial ${displaystyle mathbf {v} (0)equiv mathbf {v} _{0}}$ , que se puede expresar como la suma de componentes horizontales y verticales como sigue:

{displaystyle mathbf {v} _{0}=v_{0x}mathbf {hat {x}} +v_{0y}mathbf {hat {y}} }

Los componentes ${displaystyle v_{0x}}$ y ${displaystyle v_{0y}}$ se puede encontrar si el ángulo de lanzamiento inicial, ${displaystyle theta }$ , es conocido:

{displaystyle v_{0x}=v_{0}cos(theta)}

{displaystyle v_{0y}=v_{0}sin(theta)}

La componente horizontal de la velocidad del objeto permanece sin cambios durante todo el movimiento. La componente vertical de la velocidad cambia linealmente, porque la aceleración debida a la gravedad es constante. Las aceleraciones en las direcciones x y y se pueden integrar para resolver las componentes de la velocidad en cualquier momento t, de la siguiente manera:

{displaystyle v_{x}=v_{0}cos(theta)}

{displaystyle v_{y}=v_{0}sin(theta)-gt}

La magnitud de la velocidad (según el teorema de Pitágoras, también conocido como ley del triángulo):

{displaystyle v={sqrt {v_{x}^{2}+v_{y}^{2}}}}

Desplazamiento

En cualquier momento ${displaystyle t}$ , el desplazamiento horizontal y vertical del proyectil son:

{displaystyle x=v_{0}tcos(theta)}

{displaystyle y=v_{0}tsin(theta)-{frac {1}{2}}gt^{2}}

La magnitud del desplazamiento es:

{displaystyle Delta r={sqrt {x^{2}+y^{2}}}}

Considere las ecuaciones,

{displaystyle x=v_{0}tcos(theta),y=v_{0}tsin(theta)-{frac {1}{2}}gt^{2}}

Si se elimina t entre estas dos ecuaciones se obtiene la siguiente ecuación:

{displaystyle y=tan(theta)cdot x-{frac {g}{2v_{0}^{2}cos ^{2}theta }}cdot x^{2}=tan theta cdot xleft(1-{frac {x}{R}}right).}

Aquí R es el alcance de un proyectil.

Desde g, Silencio, y v₀ son constantes, la ecuación anterior es de la forma

{displaystyle y=ax+bx^{2}}

en el que a y b son constantes. Esta es la ecuación de una parábola, por lo que la trayectoria es parabólica. El eje de la parábola es vertical.

Si se conocen la posición del proyectil (x,y) y el ángulo de lanzamiento (θ o α), se puede encontrar la velocidad inicial resolviendo v₀ en la ecuación parabólica antes mencionada:

{displaystyle v_{0}={sqrt {{x^{2}g} over {xsin 2theta -2ycos ^{2}theta }}}}

Desplazamiento en coordenadas polares

La trayectoria parabólica de un proyectil también se puede expresar en coordenadas polares en lugar de coordenadas cartesianas. En este caso el puesto tiene la fórmula general

{displaystyle r(phi)={frac {2v_{0}^{2}cos ^{2}theta }{|g|}}left(tan theta sec phi -tan phi sec phi right)}

En esta ecuación, el origen es el punto medio de la gama horizontal del proyectil, y si el suelo es plano, el arco parabólico se parcela en el rango ${displaystyle 0leq phi leq pi }$ . Esta expresión se puede obtener mediante la transformación de la ecuación cartesiana como se indicó anteriormente ${displaystyle y=rsin phi }$ y ${displaystyle x=rcos phi }$ .

Propiedades de la trayectoria

Tiempo de vuelo o tiempo total de todo el viaje

El tiempo total t que el proyectil permanece en el aire se llama tiempo de vuelo.

{displaystyle y=v_{0}tsin(theta)-{frac {1}{2}}gt^{2}}

Después del vuelo, el proyectil vuelve al eje horizontal (x-axis), por lo que ${displaystyle y=0}$ .

{displaystyle 0=v_{0}tsin(theta)-{frac {1}{2}}gt^{2}}

{displaystyle v_{0}tsin(theta)={frac {1}{2}}gt^{2}}

{displaystyle v_{0}sin(theta)={frac {1}{2}}gt}

{displaystyle t={frac {2v_{0}sin(theta)}{|g|}}}

Tenga en cuenta que hemos despreciado la resistencia del aire en el proyectil.

Si el punto de partida está a la altura y₀ respecto del punto de impacto, el tiempo de vuelo es:

{displaystyle t={frac {d}{vcos theta }}={frac {vsin theta +{sqrt {(vsin theta)^{2}+2gy_{0}}}}{g}}}

Como arriba, esta expresión se puede reducir a

{displaystyle t={frac {vsin {theta }+{sqrt {(vsin {theta })^{2}}}}{|g|}}={frac {vsin {theta }+vsin {theta }}{|g|}}={frac {2vsin {theta }}{|g|}}={frac {2vsin {(45)}}{|g|}}={frac {2v{frac {sqrt {2}}{2}}}{|g|}}={frac {{sqrt {2}}v}{|g|}}}

si Silencio es 45° y Sí.₀ es 0.

Tiempo de vuelo hasta la posición del objetivo

Como se muestra anteriormente en el Desplazamiento sección, la velocidad horizontal y vertical de un proyectil son independientes entre sí.

Debido a esto, podemos encontrar el tiempo para alcanzar un objetivo utilizando la fórmula de desplazamiento para la velocidad horizontal:

${displaystyle x=v_{0}tcos(theta)}$

${displaystyle {frac {x}{t}}=v_{0}cos(theta)}$

${displaystyle t={frac {x}{v_{0}cos(theta)}}}$

Esta ecuación dará el tiempo total t el proyectil debe viajar para alcanzar el desplazamiento horizontal del objetivo, descuidando la resistencia al aire.

Altura máxima del proyectil

La mayor altura que alcanzará el objeto se conoce como el pico del movimiento del objeto. El aumento de la altura durará hasta ${displaystyle v_{y}=0}$ , es decir,

{displaystyle 0=v_{0}sin(theta)-gt_{h}}

Tiempo para alcanzar la altura máxima(h):

{textstyle t_{h}={frac {v_{0}sin(theta)}{|g|}}}

Para el desplazamiento vertical de la altura máxima del proyectil:

{displaystyle h=v_{0}t_{h}sin(theta)-{frac {1}{2}}gt_{h}^{2}}

{displaystyle h={frac {v_{0}^{2}sin ^{2}(theta)}{2|g|}}}

La altura máxima alcanzable se obtiene para θ=90°:

{displaystyle h_{mathrm {max} }={frac {v_{0}^{2}}{2|g|}}}

Si se conoce la posición del proyectil (x,y) y el ángulo de lanzamiento (θ), la altura máxima se puede encontrar resolviendo para h en la siguiente ecuación:

{displaystyle h={frac {(xtan theta)^{2}}{4(xtan theta -y)}}.}

Ángulo de elevación (φ) a la altura máxima se da por:

{displaystyle phi =arctan {tan theta over 2}}

Relación entre rango horizontal y altura máxima

La relación entre el rango d en el plano horizontal y la altura máxima h alcanzada ${displaystyle {frac {t_{d}}{2}}}$ es:

{displaystyle h={frac {dtan theta }{4}}}

Prueba
${displaystyle h={frac {v_{0}^{2}sin ^{2}theta }{2\|g\|}}}$ ${displaystyle d={frac {v_{0}^{2}sin 2theta }{\|g\|}}}$ ${displaystyle {frac {h}{d}}={frac {v_{0}^{2}sin ^{2}theta }{2\|g\|}}}$ × ${displaystyle {frac {g}{v_{0}^{2}sin 2theta }}}$ ${displaystyle {frac {h}{d}}={frac {sin ^{2}theta }{4sin theta cos theta }}}$ ${displaystyle h={frac {dtan theta }{4}}}$ . Si ${displaystyle h=R}$ ${displaystyle theta =arctan(4)approx 76.0^{circ }}$

Prueba

${displaystyle h={frac {v_{0}^{2}sin ^{2}theta }{2|g|}}}$

{displaystyle d={frac {v_{0}^{2}sin 2theta }{|g|}}}

{displaystyle {frac {h}{d}}={frac {v_{0}^{2}sin ^{2}theta }{2|g|}}}

{displaystyle {frac {g}{v_{0}^{2}sin 2theta }}}

{displaystyle {frac {h}{d}}={frac {sin ^{2}theta }{4sin theta cos theta }}}

${displaystyle h={frac {dtan theta }{4}}}$ .

Si ${displaystyle h=R}$

${displaystyle theta =arctan(4)approx 76.0^{circ }}$

Distancia máxima del proyectil

El rango y la altura máxima del proyectil no dependen de su masa. Por lo tanto el rango y la altura máxima son iguales para todos los cuerpos que se tiran con la misma velocidad y dirección. El rango horizontal d del proyectil es la distancia horizontal que ha recorrido cuando regresa a su altura inicial ( ${displaystyle y=0}$ ).

{displaystyle 0=v_{0}t_{d}sin(theta)-{frac {1}{2}}gt_{d}^{2}}

Hora de llegar al suelo:

{displaystyle t_{d}={frac {2v_{0}sin(theta)}{|g|}}}

Desde el desplazamiento horizontal la distancia máxima del proyectil:

{displaystyle d=v_{0}t_{d}cos(theta)}

Así que...

{displaystyle d={frac {v_{0}^{2}}{|g|}}sin(2theta)}

Tenga en cuenta que d tiene su valor máximo cuando

{displaystyle sin 2theta =1}

que necesariamente corresponde a

{displaystyle 2theta =90^{circ }}

{displaystyle theta =45^{circ }}

La distancia horizontal total (d) recorrida.

{displaystyle d={frac {vcos theta }{|g|}}left(vsin theta +{sqrt {(vsin theta)^{2}+2gy_{0}}}right)}

Cuando la superficie es plana (la altura inicial del objeto es cero), la distancia viajó:

{displaystyle d={frac {v^{2}sin(2theta)}{|g|}}}

Así se obtiene la distancia máxima si Silencio tiene 45 grados. Esta distancia es:

{displaystyle d_{mathrm {max} }={frac {v^{2}}{|g|}}}

Aplicación del teorema de la energía del trabajo

Según el teorema trabajo-energía, la componente vertical de la velocidad es:

{displaystyle v_{y}^{2}=(v_{0}sin theta)^{2}-2gy}

Estas fórmulas ignoran el arrastre aerodinámico y también suponen que el área de aterrizaje está en altura uniforme 0.

Ángulo de alcance

El "ángulo del alcance" es el ángulo (Silencio) en el que se debe lanzar un proyectil para ir a distancia d, dada la velocidad inicial v.

{displaystyle sin(2theta)={frac {gd}{v^{2}}}}

Hay dos soluciones:

{displaystyle theta ={frac {1}{2}}arcsin left({frac {gd}{v^{2}}}right)}

(Trayectoria conjunta)

y porque ${displaystyle sin(2theta)=cos(2theta -90^{circ })}$ ,

{displaystyle theta =45^{circ }+{frac {1}{2}}arccos left({frac {gd}{v^{2}}}right)}

(Trayectoria del tronco)

Ángulo θ necesario para alcanzar la coordenada (x, y)

Para alcanzar un objetivo a un alcance x y altitud y cuando se dispara desde (0,0) y con una velocidad inicial v el ángulo requerido (s) de lanzamiento θ son:

{displaystyle theta =arctan {left({frac {v^{2}pm {sqrt {v^{4}-g(gx^{2}+2yv^{2})}}}{gx}}right)}}

Las dos raíces de la ecuación corresponden a los dos posibles ángulos de lanzamiento, siempre y cuando no sean imaginarios, en cuyo caso la velocidad inicial no es lo suficientemente grande para alcanzar el punto (x,Sí.) seleccionado. Esta fórmula permite encontrar el ángulo de lanzamiento necesario sin la restricción de ${displaystyle y=0}$ .

También se puede preguntar qué ángulo de lanzamiento permite la velocidad de lanzamiento más baja posible. Esto ocurre cuando las dos soluciones anteriores son iguales, lo que implica que la cantidad bajo el signo de raíz cuadrado es cero. Esto requiere resolver una ecuación cuadrática ${displaystyle v^{2}}$ , y encontramos

{displaystyle v^{2}/g=y+{sqrt {y^{2}+x^{2}}}.}

Esto da

{displaystyle theta =arctan left(y/x+{sqrt {y^{2}/x^{2}+1}}right).}

Si denotamos el ángulo cuyo tangente es $y/x$ por $α$ Entonces

{displaystyle tan theta ={frac {sin alpha +1}{cos alpha }}}

{displaystyle tan(pi /2-theta)={frac {cos alpha }{sin alpha +1}}}

{displaystyle cos ^{2}(pi /2-theta)={frac {1}{2}}(sin alpha +1)}

{displaystyle 2cos ^{2}(pi /2-theta)-1=cos(pi /2-alpha)}

Esto implica

{displaystyle theta =pi /2-{frac {1}{2}}(pi /2-alpha).}

En otras palabras, el lanzamiento debe realizarse en el ángulo medio entre el objetivo y el cenit (vector opuesto a la gravedad).

Longitud total del recorrido de la trayectoria

La longitud del arco parabólico trazado por un proyectil L, dado que la altura de lanzamiento y aterrizaje es la misma y que no hay resistencia del aire, viene dada por la fórmula:

{displaystyle L={frac {v_{0}^{2}}{2g}}left(2sin theta +cos ^{2}theta cdot ln {frac {1+sin theta }{1-sin theta }}right)={frac {v_{0}^{2}}{g}}left(sin theta +cos ^{2}theta cdot tanh ^{-1}(sin theta)right)}

Donde ${displaystyle v_{0}}$ es la velocidad inicial, ${displaystyle theta }$ es el ángulo de lanzamiento y ${displaystyle g}$ es la aceleración debido a la gravedad como un valor positivo. La expresión puede obtenerse evaluando la longitud del arco integral para la parabola de alta distancia entre los límites inicial y final desplazamientos (es decir, entre 0 y la gama horizontal del proyectil) tales que:

{displaystyle L=int _{0}^{mathrm {range} }{sqrt {1+left({frac {mathrm {d} y}{mathrm {d} x}}right)^{2}}},mathrm {d} x=int _{0}^{v_{0}^{2}sin(2theta)/g}{sqrt {1+left(tan theta -{g over {v_{0}^{2}cos ^{2}theta }}xright)^{2}}},mathrm {d} x.}

Si el tiempo de vuelo es t,

{displaystyle L=int _{0}^{t}{sqrt {v_{x}^{2}+v_{y}^{2}}},mathrm {d} t=int _{0}^{2v_{0}sin theta /g}{sqrt {(gt)^{2}-2gv_{0}sin theta t+v_{0}^{2}}},mathrm {d} t.}

Trayectoria de un proyectil con resistencia del aire

Trayectorias de una masa lanzada a un ángulo de 70°:
sin arrastrar
con la arrastre de Stokes
con arrastre Newtonian

La resistencia al aire crea una fuerza que (para proyectiles simétricos) siempre está dirigida contra la dirección del movimiento en el medio circundante y tiene una magnitud que depende de la velocidad absoluta: ${displaystyle mathbf {F_{air}} =-f(v)cdot mathbf {hat {v}} }$ . La dependencia de velocidad de la fuerza de fricción es lineal ( ${displaystyle f(v)propto v}$ ) a velocidades muy bajas (Stokes drag) y quadratic ( ${displaystyle f(v)propto v^{2}}$ ) a velocidades más grandes (Newton drag). La transición entre estos comportamientos está determinada por el número Reynolds, que depende de la velocidad, el tamaño del objeto y la viscosidad cinemática del medio. Para Reynolds números inferiores a unos 1000, la dependencia es lineal, por encima se vuelve cuadrática. En el aire, que tiene una viscosidad cinemática alrededor ${displaystyle 0.15,mathrm {cm^{2}/s} }$ , esto significa que la fuerza de arrastre se vuelve cuadrática en v cuando el producto de velocidad y diámetro es más que alrededor ${displaystyle 0.015,mathrm {m^{2}/s} }$ , que es típicamente el caso de los proyectiles.

Stokes arrastra: ${displaystyle mathbf {F_{air}} =-k_{mathrm {Stokes} }cdot mathbf {v} qquad }$ (por ${displaystyle Relesssim 1000}$ )
Newton drag: ${displaystyle mathbf {F_{air}} =-k,|mathbf {v} |cdot mathbf {v} qquad }$ (por ${displaystyle Regtrsim 1000}$ )

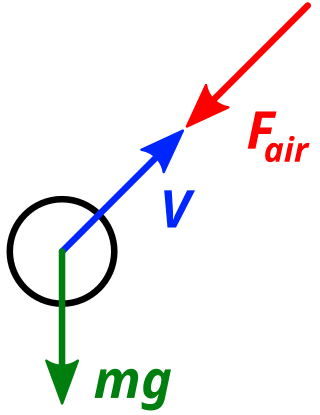
El diagrama de cuerpo libre a la derecha es para un proyectil que experimenta resistencia al aire y los efectos de la gravedad. Aquí se supone que la resistencia al aire está en la dirección opuesta a la velocidad del proyectil: ${displaystyle mathbf {F_{mathrm {air} }} =-f(v)cdot mathbf {hat {v}} }$

Trayectoria de un proyectil con arrastre de Stokes

Stokes drag, donde ${displaystyle mathbf {F_{air}} propto mathbf {v} }$ , sólo se aplica a muy baja velocidad en el aire, y por lo tanto no es el caso típico de los proyectiles. Sin embargo, la dependencia lineal de ${displaystyle F_{mathrm {air} }}$ on ${displaystyle v}$ causa una ecuación diferencial muy simple del movimiento

{displaystyle {frac {mathrm {d} }{mathrm {d} t}}{begin{pmatrix}v_{x}\v_{y}end{pmatrix}}={begin{pmatrix}-mu ,v_{x}\-g-mu ,v_{y}end{pmatrix}}}

en el que los dos componentes cartesianos se vuelven completamente independientes, y por lo tanto más fácil de resolver. Aquí, ${displaystyle v_{0}}$ , ${displaystyle v_{x}}$ y ${displaystyle v_{y}}$ se utilizará para denotar la velocidad inicial, la velocidad a lo largo de la dirección x y la velocidad en la dirección Sí., respectivamente. La masa del proyectil será denotada por m, y ${displaystyle mu:=k/m}$ . Para la derivación sólo el caso donde ${displaystyle 0^{o}leq theta leq 180^{o}}$ se considera. De nuevo, el proyectil se despide del origen (0,0).

Derivación de posición horizontal
Las relaciones que representan el movimiento de la partícula se derivan de la Segunda Ley de Newton, tanto en las direcciones x y y. En la dirección x ${displaystyle Sigma F=-kv_{x}=ma_{x}}$ y en la dirección y ${displaystyle Sigma F=-kv_{y}-mg=ma_{y}}$ . Esto implica que: ${displaystyle a_{x}=-mu v_{x}={frac {mathrm {d} v_{x}}{mathrm {d} t}}}$ 1) y ${displaystyle a_{y}=-mu v_{y}-g={frac {mathrm {d} v_{y}}{mathrm {d} t}}}$ 2) Solving (1) es una ecuación diferencial elemental, por lo tanto los pasos conducen a una solución única para `v_x` y, posteriormente, `x` no se enumerará. Dadas las condiciones iniciales ${displaystyle v_{x}=v_{x0}}$ (donde) `v_x0` se entiende que es el componente x de la velocidad inicial) y ${displaystyle x=0}$ para ${displaystyle t=0}$ : ${displaystyle v_{x}=v_{x0}e^{-mu t}}$ (1a)

Derivación de posición horizontal

Las relaciones que representan el movimiento de la partícula se derivan de la Segunda Ley de Newton, tanto en las direcciones x y y. En la dirección x ${displaystyle Sigma F=-kv_{x}=ma_{x}}$ y en la dirección y ${displaystyle Sigma F=-kv_{y}-mg=ma_{y}}$ .

Esto implica que:

${displaystyle a_{x}=-mu v_{x}={frac {mathrm {d} v_{x}}{mathrm {d} t}}}$ 1)

${displaystyle a_{y}=-mu v_{y}-g={frac {mathrm {d} v_{y}}{mathrm {d} t}}}$ 2)

Solving (1) es una ecuación diferencial elemental, por lo tanto los pasos conducen a una solución única para v_x y, posteriormente, x no se enumerará. Dadas las condiciones iniciales ${displaystyle v_{x}=v_{x0}}$ (donde) v_x0 se entiende que es el componente x de la velocidad inicial) y ${displaystyle x=0}$ para ${displaystyle t=0}$ :

${displaystyle v_{x}=v_{x0}e^{-mu t}}$ (1a)

{displaystyle x(t)={frac {v_{x0}}{mu }}left(1-e^{-mu t}right)}

(1b)

Derivación de posición vertical
Si bien (1) se resuelve mucho de la misma manera, (2) es de interés distinto debido a su naturaleza no homogénea. Por lo tanto, vamos a resolver ampliamente (2). Tenga en cuenta que en este caso se utilizan las condiciones iniciales ${displaystyle v_{y}=v_{y0}}$ y ${displaystyle y=0}$ cuando ${displaystyle t=0}$ . ${displaystyle {frac {mathrm {d} v_{y}}{mathrm {d} t}}=-mu v_{y}-g}$ 2) ${displaystyle {frac {mathrm {d} v_{y}}{mathrm {d} t}}+mu v_{y}=-g}$ (2a) Esta primera orden, ecuación diferencial lineal y no homogénea puede resolverse de varias maneras; sin embargo, en este caso, será más rápido acercarse a la solución a través de un factor integrador ${displaystyle e^{int mu ,mathrm {d} t}}$ . ${displaystyle e^{mu t}({frac {mathrm {d} v_{y}}{mathrm {d} t}}+mu v_{y})=e^{mu t}(-g)}$ (2c) ${displaystyle (e^{mu t}v_{y})^{prime }=e^{mu t}(-g)}$ (2d) ${displaystyle int {(e^{mu t}v_{y})^{prime },mathrm {d} t}=e^{mu t}v_{y}=int {e^{mu t}(-g),mathrm {d} t}}$ (2e) ${displaystyle e^{mu t}v_{y}={frac {1}{mu }}e^{mu t}(-g)+C}$ (2f) ${displaystyle v_{y}={frac {-g}{mu }}+Ce^{-mu t}}$ (2g) Y por integración encontramos: ${displaystyle y=-{frac {g}{mu }}t-{frac {1}{mu }}(v_{y0}+{frac {g}{mu }})e^{-mu t}+C}$ 3) Resolver nuestras condiciones iniciales: ${displaystyle v_{y}(t)=-{frac {g}{mu }}+(v_{y0}+{frac {g}{mu }})e^{-mu t}}$ (2h) ${displaystyle y(t)=-{frac {g}{mu }}t-{frac {1}{mu }}(v_{y0}+{frac {g}{mu }})e^{-mu t}+{frac {1}{mu }}(v_{y0}+{frac {g}{mu }})}$ (3a) Con un poco de álgebra para simplificar (3a):

Derivación de posición vertical

Si bien (1) se resuelve mucho de la misma manera, (2) es de interés distinto debido a su naturaleza no homogénea. Por lo tanto, vamos a resolver ampliamente (2). Tenga en cuenta que en este caso se utilizan las condiciones iniciales ${displaystyle v_{y}=v_{y0}}$ y ${displaystyle y=0}$ cuando ${displaystyle t=0}$ .

${displaystyle {frac {mathrm {d} v_{y}}{mathrm {d} t}}=-mu v_{y}-g}$ 2)

${displaystyle {frac {mathrm {d} v_{y}}{mathrm {d} t}}+mu v_{y}=-g}$ (2a)

Esta primera orden, ecuación diferencial lineal y no homogénea puede resolverse de varias maneras; sin embargo, en este caso, será más rápido acercarse a la solución a través de un factor integrador ${displaystyle e^{int mu ,mathrm {d} t}}$ .

${displaystyle e^{mu t}({frac {mathrm {d} v_{y}}{mathrm {d} t}}+mu v_{y})=e^{mu t}(-g)}$ (2c)

${displaystyle (e^{mu t}v_{y})^{prime }=e^{mu t}(-g)}$ (2d)

${displaystyle int {(e^{mu t}v_{y})^{prime },mathrm {d} t}=e^{mu t}v_{y}=int {e^{mu t}(-g),mathrm {d} t}}$ (2e)

${displaystyle e^{mu t}v_{y}={frac {1}{mu }}e^{mu t}(-g)+C}$ (2f)

${displaystyle v_{y}={frac {-g}{mu }}+Ce^{-mu t}}$ (2g)

Y por integración encontramos:

${displaystyle y=-{frac {g}{mu }}t-{frac {1}{mu }}(v_{y0}+{frac {g}{mu }})e^{-mu t}+C}$ 3)

Resolver nuestras condiciones iniciales:

${displaystyle v_{y}(t)=-{frac {g}{mu }}+(v_{y0}+{frac {g}{mu }})e^{-mu t}}$ (2h)

${displaystyle y(t)=-{frac {g}{mu }}t-{frac {1}{mu }}(v_{y0}+{frac {g}{mu }})e^{-mu t}+{frac {1}{mu }}(v_{y0}+{frac {g}{mu }})}$ (3a)

Con un poco de álgebra para simplificar (3a):

{displaystyle y(t)=-{frac {g}{mu }}t+{frac {1}{mu }}left(v_{y0}+{frac {g}{mu }}right)left(1-e^{-mu t}right)}

(3b)

Derivación del tiempo de vuelo
El tiempo total del viaje en presencia de la resistencia al aire (más específicamente, cuando ${displaystyle F_{air}=-kv}$ ) se puede calcular por la misma estrategia que arriba, es decir, resolvemos la ecuación ${displaystyle y(t)=0}$ . Mientras que en el caso de la resistencia al aire cero esta ecuación se puede resolver de manera elemental, aquí necesitamos la función Lambert W. La ecuación ${displaystyle y(t)=-{frac {g}{mu }}t+{frac {1}{mu }}(v_{y0}+{frac {g}{mu }})(1-e^{-mu t})=0}$ es de la forma ${displaystyle c_{1}t+c_{2}+c_{3}e^{c_{4}t}=0}$ , y tal ecuación se puede transformar en una ecuación solvable por el ${displaystyle W}$ función (ver un ejemplo de tal transformación aquí). Algunos álgebra muestra que el tiempo total del vuelo, en forma cerrada, se da como

Derivación del tiempo de vuelo

El tiempo total del viaje en presencia de la resistencia al aire (más específicamente, cuando ${displaystyle F_{air}=-kv}$ ) se puede calcular por la misma estrategia que arriba, es decir, resolvemos la ecuación ${displaystyle y(t)=0}$ . Mientras que en el caso de la resistencia al aire cero esta ecuación se puede resolver de manera elemental, aquí necesitamos la función Lambert W. La ecuación ${displaystyle y(t)=-{frac {g}{mu }}t+{frac {1}{mu }}(v_{y0}+{frac {g}{mu }})(1-e^{-mu t})=0}$ es de la forma ${displaystyle c_{1}t+c_{2}+c_{3}e^{c_{4}t}=0}$ , y tal ecuación se puede transformar en una ecuación solvable por el ${displaystyle W}$ función (ver un ejemplo de tal transformación aquí). Algunos álgebra muestra que el tiempo total del vuelo, en forma cerrada, se da como

{displaystyle t={frac {1}{mu }}left(1+{frac {mu }{g}}v_{y0}+Wleft(-left(1+{frac {mu }{g}}v_{y0}right)e^{-left(1+{frac {mu }{g}}v_{y0}right)}right)right)}

Trayectoria de un proyectil con arrastre de Newton

El caso más típico de resistencia al aire, para el caso de los números de Reynolds por encima de 1000 es la arrastre Newton con una fuerza de arrastre proporcional a la velocidad cuadrada, ${displaystyle F_{mathrm {air} }=-kv^{2}}$ . En el aire, que tiene una viscosidad cinemática alrededor ${displaystyle 0.15,mathrm {cm^{2}/s} }$ , esto significa que el producto de velocidad y diámetro debe ser más que cerca ${displaystyle 0.015,mathrm {m^{2}/s} }$ .

Desafortunadamente, las ecuaciones de movimiento pueden no ser fácilmente resuelto analíticamente para este caso. Por lo tanto, se examinará una solución numérica.

Se hacen las siguientes suposiciones:

Aceleración gravitatoria constante
La resistencia al aire es dada por la siguiente fórmula de arrastre,

{displaystyle mathbf {F_{D}} =-{tfrac {1}{2}}crho A,v,mathbf {v} }

Donde:

F_D es la fuerza de arrastre
c es el coeficiente de resistencia
*** es la densidad del aire
A es el área transversal del proyectil
μ = k/m = cρA/(2)m)

Casos especiales

Aunque el caso general de un proyectil con arrastre Newton no puede ser resuelto analíticamente, algunos casos especiales pueden. Aquí denotamos la velocidad terminal en caída libre como ${displaystyle v_{infty }={sqrt {g/mu }}}$ y el tiempo de ajuste característico constante ${displaystyle t_{f}=1/{sqrt {gmu }}}$ .

Movimiento casi horizontal: En caso de que el movimiento sea casi horizontal, ${displaystyle |v_{x}|gg |v_{y}|}$ , como una bala voladora, el componente de velocidad vertical tiene muy poca influencia en el movimiento horizontal. En este caso:

{displaystyle {dot {v}}_{x}(t)=-mu ,v_{x}^{2}(t)}

{displaystyle v_{x}(t)={frac {1}{1/v_{x,0}+mu ,t}}}

{displaystyle x(t)={frac {1}{mu }}ln(1+mu ,v_{x,0}cdot t)}

El mismo patrón se aplica para el movimiento con fricción a lo largo de una línea en cualquier dirección, cuando la gravedad es insignificante. También se aplica cuando se evita el movimiento vertical, como para un coche en movimiento con su motor apagado.

Movimiento vertical hacia arriba:

{displaystyle {dot {v}}_{y}(t)=-g-mu ,v_{y}^{2}(t)}

{displaystyle v_{y}(t)=v_{infty }tan {frac {t_{mathrm {peak} }-t}{t_{f}}}}

{displaystyle y(t)=y_{mathrm {peak} }+{frac {1}{mu }}ln left(cos {frac {t_{mathrm {peak} }-t}{t_{f}}}right)}

Aquí.

{displaystyle v_{infty }equiv {sqrt {frac {g}{mu }}},}

{displaystyle t_{f}equiv {frac {1}{sqrt {mu g}}},}

{displaystyle t_{mathrm {peak} }equiv t_{f}arctan {frac {v_{y,0}}{v_{infty }}}={frac {1}{sqrt {mu g}}}arctan {left({sqrt {frac {mu }{g}}}v_{y,0}right)},}

{displaystyle y_{mathrm {peak} }equiv -{frac {1}{mu }}ln {cos {frac {t_{mathrm {peak} }}{t_{f}}}}={frac {1}{2mu }}ln {left(1+{frac {mu }{g}}v_{y,0}^{2}right)}}

Donde

{displaystyle v_{y,0}}

es la velocidad inicial ascendente a

{displaystyle t=0}

y la posición inicial

{displaystyle y(0)=0}

Un proyectil no puede aumentar más que

{displaystyle t_{mathrm {rise} }={frac {pi }{2}}t_{f}}

en la dirección vertical antes de alcanzar el pico.

Movimiento vertical hacia abajo:

{displaystyle {dot {v}}_{y}(t)=-g+mu ,v_{y}^{2}(t)}

{displaystyle v_{y}(t)=-v_{infty }tanh {frac {t-t_{mathrm {peak} }}{t_{f}}}}

{displaystyle y(t)=y_{mathrm {peak} }-{frac {1}{mu }}ln left(cosh {frac {t-t_{mathrm {peak} }}{t_{f}}}right)}

Después de un tiempo

{displaystyle t_{f}}

, el proyectil alcanza casi velocidad terminal

{displaystyle -v_{infty }}

Solución numérica

El movimiento de un proyectil con arrastre se puede calcular genéricamente mediante la integración numérica de la ecuación diferencial ordinaria, por ejemplo, aplicando una reducción a un sistema de primer orden. La ecuación a resolver es

{displaystyle {frac {mathrm {d} }{mathrm {d} t}}{begin{pmatrix}x\y\v_{x}\v_{y}end{pmatrix}}={begin{pmatrix}v_{x}\v_{y}\-mu ,v_{x}{sqrt {v_{x}^{2}+v_{y}^{2}}}\-g-mu ,v_{y}{sqrt {v_{x}^{2}+v_{y}^{2}}}end{pmatrix}}}

Este enfoque también permite agregar los efectos del coeficiente de resistencia dependiente de la velocidad, la densidad del aire dependiente de la altitud y el campo de gravedad dependiente de la posición.

Trayectoria elevada

Un caso especial de trayectoria balística para un cohete es una trayectoria elevada, una trayectoria con un apogeo mayor que la trayectoria de energía mínima al mismo rango. En otras palabras, el cohete viaja más alto y al hacerlo utiliza más energía para llegar al mismo punto de aterrizaje. Esto se puede hacer por varias razones, como aumentar la distancia al horizonte para brindar un mayor rango de visión/comunicación o para cambiar el ángulo con el que impactará un misil al aterrizar. Las trayectorias elevadas se utilizan a veces tanto en cohetes de misiles como en vuelos espaciales.

Movimiento de proyectiles a escala planetaria

Trayectoria proyectil alrededor de un planeta, en comparación con el movimiento en un campo uniforme

Cuando un proyectil sin resistencia del aire recorre una distancia significativa en comparación con el radio de la Tierra (por encima de ≈100 km), la curvatura de la Tierra y la gravedad no uniforme de la Tierra tienen que ser consideró. Éste es el caso, por ejemplo, de las naves espaciales o de los proyectiles intercontinentales. Luego, la trayectoria se generaliza desde una parábola hasta una elipse de Kepler con un foco en el centro de la Tierra. El movimiento del proyectil sigue entonces las leyes del movimiento planetario de Kepler.

Los parámetros de las trayectorias deben adaptarse de los valores de un campo de gravedad uniforme indicado anteriormente. El radio terrestre se toma como R, y g como la gravedad de la superficie estándar. Vamos. ${displaystyle {tilde {v}}:=v/{sqrt {Rg}}}$ la velocidad de lanzamiento relativa a la primera velocidad cósmica.

Rango total d entre el lanzamiento y el impacto:

{displaystyle d={frac {v^{2}sin(2theta)}{g}}{Big /}{sqrt {1-left(2-{tilde {v}}^{2}right){tilde {v}}^{2}cos ^{2}theta }}}

Rango máximo de un proyectil para un ángulo de lanzamiento óptimo ( ${displaystyle theta ={tfrac {1}{2}}arccos left({tilde {v}}^{2}/(2-{tilde {v}}^{2})right)}$ ):