Mosaico rombitrihexagonal
| Tiling Rhombitrihexagonal | |
|---|---|
 | |
| Tipo | Tiling semiregular |
| Configuración de Vertex |  3.4.6.4 |
| Símbolo Schläfli | o r{}63}{displaystyle r{begin{Bmatrix}63end{Bmatrix}} |
| Signatura Wythoff | 3 Silencio 6 2 |
| Coxeter diagrama |     |
| Simmetría | p6m, [6,3], (*632) |
| Simetría de rotación | p6, [6,3]+, (632) |
| Bowers acronym | Rothat |
| Doble | Tiling trihexagonal Deltoidal |
| Propiedades | Vertex-transitive |
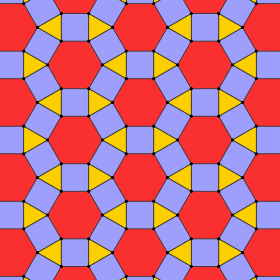
En geometría, el mosaico rombitrihexagonal es un mosaico semirregular del plano euclidiano. Hay un triángulo, dos cuadrados y un hexágono en cada vértice. Tiene el símbolo Schläfli de rr{3,6}.
John Conway lo llama rombihexadeltille. Puede considerarse un cantelado según la terminología de Norman Johnson o un mosaico hexagonal expandido según el lenguaje operativo de Alicia Boole Stott.
Hay tres mosaicos regulares y ocho semirregulares en el plano.
Colorantes uniformes
Solo hay una coloración uniforme en un mosaico rombitrihexagonal. (Nombrar los colores por índices alrededor de un vértice (3.4.6.4): 1232.)
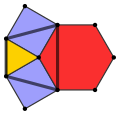
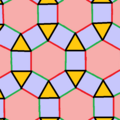
Con los colores de borde hay una media forma de simetría (3*3) notación de orbifold. Los hexágonos pueden considerarse como triángulos truncados, t{3} con dos tipos de bordes. Tiene el diagrama de Coxeter 
, símbolo Schläfli s2{3,6}. La plaza bicolor se puede distorsionar en isosceles trapezoids. En el límite, donde los rectángulos degeneran en bordes, resultados de baldosas triangulares, construidos como una baldosa triangular, .
| Simmetría | [6,3], (*632) | [6,3]+], (3*3) | ||
|---|---|---|---|---|
| Nombre | Rhombitrihexagonal | Cantic snub triangular | Snub triangular | |
| Imagen |  Coloración de cara uniforme |  Colorante de borde uniforme |  Geometría no uniforme |  Limit |
| Schläflisymbol | rr{3,6} | s2{3,6} | S{3,6} | |
| Coxeterdiagram | | | | |
Ejemplos
 Desde El Gramática del Ornamento (1856) | 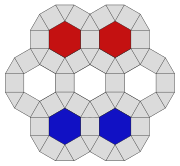 El juego Kensington |  Suelos, Museo Arqueológico de Sevilla, Sevilla, España |  El Templo de Diana en Nîmes, Francia |  mosaico de suelo romano en Castel di Guido |
Mosaicos relacionados
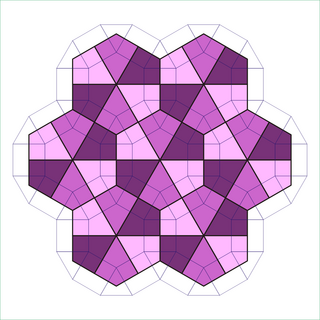
Hay un mosaico de 2 uniformes relacionado, que tiene hexágonos disecados en seis triángulos. El mosaico rombitrihexagonal también está relacionado con el mosaico trihexagonal truncado al reemplazar algunos de los hexágonos y los cuadrados y triángulos circundantes con dodecágonos:
| 1-uniform | Disección | Disecciones de 2 unidades | |
|---|---|---|---|
 3.4.6.4 |  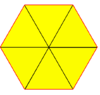 |  3.3.4.3.4 " 36 |  a CH |
| Azulejos dobles | |||
 3.4.6.4 |   |  4.6.12 |  a 3 |
Embalaje circular
El mosaico rombitrihexagonal se puede utilizar como empaquetamiento de círculos, colocando círculos de igual diámetro en el centro de cada punto. Cada círculo está en contacto con otros cuatro círculos del embalaje (número de beso). El dominio de red traslacional (rombo rojo) contiene seis círculos distintos.
Construcción Wythoff
Hay ocho mosaicos uniformes que pueden basarse en el mosaico hexagonal regular (o el mosaico triangular dual).
Al dibujar los mosaicos coloreados de rojo en las caras originales, amarillo en los vértices originales y azul a lo largo de los bordes originales, hay ocho formas, siete topológicamente distintas. (El mosaico triangular truncado es topológicamente idéntico al mosaico hexagonal).
| Sellos hexagonales/triangulares uniformes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simmetría: [6,3], (*632) | [6,3]+ (632) | [6,3]+] (3*3) | |||||||||
| {6,3} | t{6,3} | r{6,3} | t{3,6} | {3,6} | rr{6,3} | tr{6,3} | sr{6,3} | S{3,6} | |||
| | | | | | | | | |||
 |  |  |  |  |  |  |  |  | |||
| 63 | 3.122 | (3.6)2 | 6.6.6 | 36 | 3.4.6.4 | 4.6.12 | 3.3.3.6 | 3.3.3.3.3.3 | |||
| Uniformes duales | |||||||||||
 |  |  | |  |  |  |  | | |||
| V63 | V3.122 | V(3.6)2 | V63 | V36 | V3.4.6.4 | V.4.6.12 | V34.6 | V36 | |||
Mutaciones de simetría
Este mosaico está relacionado topológicamente como parte de una secuencia de poliedros cantelados con figura de vértice (3.4.n.4), y continúa como mosaicos del plano hiperbólico. Estas figuras transitivas de vértice tienen (*n32) simetría reflexiva.
| *n32 mutación simetría de los revestimientos ampliados: 3.4.n.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Simmetría *n32 [n,3] | Spherical | Euclid. | Hiperb compacto. | Paracomp. | ||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | |
| Gráfico |  |  |  |  |  |  |  |  |
| Config. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4. |
Mosaico trihexagonal deltoidal
El mosaico trihexagonal deltoidal es un mosaico dual del mosaico semirregular conocido como mosaico rombitrihexagonal. Conway lo llama tetrille. Los bordes de este mosaico pueden formarse mediante la superposición de intersección del mosaico triangular regular y un mosaico hexagonal. Cada cara de cometa de este mosaico tiene ángulos de 120°, 90°, 60° y 90°. Es uno de los ocho mosaicos del plano en el que cada borde se encuentra en un eje de simetría del mosaico.
El mosaico trihexagonal deltoidal es un mosaico dual del mosaico semirregular rombitrihexagonal. Sus caras son deltoides o cometas.
Poliedros y mosaicos relacionados
Es uno de los siete mosaicos uniformes duales en simetría hexagonal, incluidos los duales regulares.
| Simmetría: [6,3], (*632) | [6,3]+, (632) | |||||
|---|---|---|---|---|---|---|
|  |  | |  |  |  |
| V63 | V3.122 | V(3.6)2 | V36 | V3.4.6.4 | V.4.6.12 | V34.6 |
Este mosaico tiene variaciones transitivas de caras, que pueden distorsionar las cometas en trapecios bilaterales o cuadriláteros más generales. Haciendo caso omiso de los colores de la cara a continuación, la simetría total es p6m y la simetría inferior es p31m con tres espejos que se encuentran en un punto y tres puntos de rotación.
| Simmetría | p6m, [6,3], (*632) | p31m, [6,3+], (3*3) | |
|---|---|---|---|
| Formulario |  |  |  |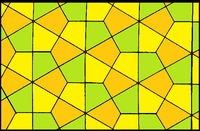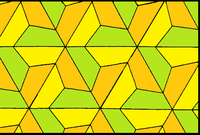
| Caras | Kite | Medio hexagonal regular | Cuadrilaterals |
Este mosaico está relacionado con el mosaico trihexagonal al dividir los triángulos y hexágonos en triángulos centrales y fusionar los triángulos vecinos en cometas.
El mosaico trihexagonal deltoidal es parte de un conjunto de mosaicos duales uniformes, correspondientes al dual del mosaico rombitrihexagonal.
Mutaciones de simetría
Este mosaico está relacionado topológicamente como parte de la secuencia de mosaicos con configuraciones de cara V3.4.n.4, y continúa como mosaicos del plano hiperbólico. Estas figuras transitivas de caras tienen (*n32) simetría reflexiva.
| Simmetría *n32 [n,3] | Spherical | Euclid. | Hiperb compacto. | Paraco. | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | |
| Gráfico Config. |  V3.4.2.4 |  V3.4.3.4 |  V3.4.4.4 |  V3.4.5.4 | V3.4.6.4 |  V3.4.7.4 |  V3.4.8.4 |  V3.4.∞.4 |
Otros mosaicos deltoidales (cometa)
Son posibles otros mosaicos deltoidales.
La simetría de puntos permite que el plano se llene con cometas en crecimiento, con la topología como un mosaico cuadrado, V4.4.4.4, y se puede crear cruzando la cuerda de un atrapasueños. A continuación se muestra un ejemplo con simetría hexagonal diédrica.
Otro mosaico transitivo de caras con caras en forma de cometa, también una variación topológica de un mosaico cuadrado y con configuración de caras V4.4.4.4. También es transitivo de vértice, y cada vértice contiene todas las orientaciones de la cara de la cometa.
| Simmetría | D6, [6], (*66) | p.m.+], (22*) | p6m, [6,3], (*632) |
|---|---|---|---|
| Tiling |  |  | |
| Configuración | V4.4.4.4 | V6.4.3.4 | |