Mosaico pentagonal de El Cairo
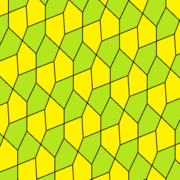
En geometría, un mosaico pentagonal de El Cairo es una teselación del plano euclidiano por pentágonos convexos congruentes, formada superponiendo dos teselaciones del plano por hexágonos y llamada así por su uso como diseño de pavimento en El Cairo. . También se la llama red de MacMahon en honor a Percy Alexander MacMahon, quien la describió en su publicación de 1921 Nuevos pasatiempos matemáticos. John Horton Conway lo llamó pentilla cuádruple.
Infinidad de pentágonos diferentes pueden formar este patrón, pertenecientes a dos de las 15 familias de pentágonos convexos que pueden formar mosaicos en el plano. Sus mosaicos tienen diferentes simetrías; todos son simétricos en la cara. Una forma particular de alicatado, dual al alicatado cuadrado chato, presenta baldosas con el mínimo perímetro posible entre todos los alicatados pentagonales. Otra, la superposición de dos mosaicos aplanados por hexágonos regulares, es la forma utilizada en El Cairo y tiene la propiedad de que cada arista es colineal con una infinidad de otras aristas.
En arquitectura, más allá de El Cairo, los azulejos de El Cairo se han utilizado en la arquitectura mogol en la India del siglo XVIII, en Laeiszhalle de principios del siglo XX en Alemania y en muchos edificios e instalaciones modernos. También se ha estudiado como estructura cristalina y aparece en el arte de M. C. Escher.
Estructura y clasificación
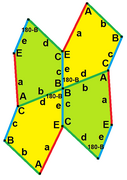
La unión de todas las aristas de un mosaico Cairo es la misma que la unión de dos mosaicos del plano mediante hexágonos. Cada hexágono de un mosaico rodea dos vértices del otro mosaico y está dividido por los hexágonos del otro mosaico en cuatro de los pentágonos del mosaico de El Cairo. Infinidad de pentágonos diferentes pueden formar mosaicos de El Cairo, todos con el mismo patrón de adyacencias entre mosaicos y con la misma descomposición en hexágonos, pero con diferentes longitudes de bordes, ángulos y simetrías. Los pentágonos que forman estos mosaicos se pueden agrupar en dos familias infinitas diferentes, extraídas de las 15 familias de pentágonos convexos que pueden mosaicos del plano, y las cinco familias de pentágonos encontradas por Karl Reinhardt en 1918 que pueden mosaicos del plano isoédrico (todos los mosaicos simétricos entre sí).
Una de estas dos familias consta de pentágonos que tienen dos ángulos rectos no adyacentes, con un par de lados de igual longitud que se encuentran en cada uno de estos ángulos rectos. Cualquier pentágono que cumpla estos requisitos mosaico el plano mediante copias que, en las esquinas en ángulo recto elegidas, giran un ángulo recto entre sí. En los lados del pentágono que no son adyacentes a uno de estos dos ángulos rectos, se encuentran dos fichas que giran un ángulo de 180° entre sí. El resultado es un mosaico isoédrico, lo que significa que cualquier pentágono del mosaico puede transformarse en cualquier otro pentágono mediante una simetría del mosaico. Estos pentágonos y sus mosaicos a menudo se enumeran como "tipo 4" en el listado de tipos de pentágono que pueden colocarse en mosaico. Para cualquier mosaico tipo 4 Cairo, doce de los mismos mosaicos también pueden cubrir la superficie de un cubo, con un mosaico doblado a lo largo de cada borde del cubo y tres ángulos rectos de mosaicos que se juntan en cada vértice del cubo, para formar la misma estructura combinatoria que un mosaico regular. dodecaedro.
La otra familia de pentágonos que forman el mosaico de El Cairo son pentágonos que tienen dos ángulos complementarios en vértices no adyacentes, cada uno con las mismas dos longitudes de lados incidentes. En sus mosaicos, los vértices con ángulos complementarios se alternan alrededor de cada vértice de grado cuatro. Los pentágonos que cumplen estas restricciones. generalmente no figuran como una de las 15 familias de pentágonos que aparecen en mosaico; más bien, son parte de una familia más grande de pentágonos (los pentágonos “tipo 2”) que recubren el plano isoédricamente de una manera diferente.
Simétrica bilateral Los revestimientos de El Cairo están formados por pentágonos que pertenecen tanto al tipo 2 como al tipo 4 familias. El patrón de pavimentación de ladrillo de canasta se puede ver como un caso degenerado de los azulejos de El Cairo bilateralmente simétricos, con cada ladrillo (a rectángulo) interpretado como un pentágono con cuatro ángulos rectos y un ángulo de 180°.
- Tipo 2 Los azulejos de El Cairo tienen ángulos complementarios no adyacentes, con las mismas dos longitudes laterales adyacentes
- Tipo 4 azulejos tienen ángulos rectos no adyacentes entre pares de lados de longitud igual
- Las baldosas bilateralmente simétricas (que pertenecen a ambos tipos) usan las baldosas con ángulos rectos no adyacentes y cuatro bordes iguales
- Tipo 2 Azulejos de El Cairo, con coloración mostrando azulejos reflejados y no reflejados
- En un nivel de El Cairo tipo 4, los pentágonos pueden ser bilateralmente simétricos incluso cuando el revestimiento no es
- La canasta, una baldosa bilateralmente simétrica degenerada, con solapa no degenerada
Es posible asignar coordenadas de medio entero de seis dimensiones a los pentágonos de la baldosa, de tal manera que el número de pasos de borde a filo entre cualquier dos pentágonos equivale a la distancia L1 entre sus coordenadas. Las seis coordenadas de cada pentágono se pueden agrupar en dos triples de coordenadas, en las que cada triple da las coordenadas de un hexágono en un sistema análogo de coordenadas tridimensionales para cada uno de los dos revestimientos hexagonales superpuestos. El número de fichas que son pasos lejos de cualquier ficha dada, , se da por la secuencia de coordinación
Casos especiales
Azulejos catalanes
El revestimiento cuadrado de snub, hecho de dos cuadrados y tres triángulos equiláteros alrededor de cada vértice, tiene un nivel de El Cairo bilateralmente simétrico como su doble inclinación. El azulejo de El Cairo se puede formar desde el revestimiento cuadrado de snub colocando un vértice del azulejo de El Cairo en el centro de cada cuadrado o triángulo del azulejo cuadrado de snub, y conectando estos vértices por bordes cuando vienen de las baldosas adyacentes. Sus pentágonos pueden circunscribirse alrededor de un círculo. Tienen cuatro bordes largos y uno corto con longitudes en la relación . Los ángulos de estos pentágonos forman la secuencia 120°, 120°, 90°, 120°, 90°.
El mosaico cuadrado chato es un mosaico de Arquímedes y, como dual de un mosaico de Arquímedes, esta forma del mosaico pentagonal de El Cairo es un mosaico catalán o mosaico de Laves. Es uno de los dos mosaicos pentagonales monoédricos que, cuando los mosaicos tienen un área unitaria, minimiza el perímetro de los mosaicos. El otro es también un mosaico por pentágonos circunscritos con dos ángulos rectos y tres ángulos de 120°, pero con los dos ángulos rectos adyacentes; También hay infinitos mosaicos formados combinando ambos tipos de pentágono.
Mosaico con bordes colineales

Pentágonos con coordenadas de vertex entero , , y , con cuatro lados iguales más cortos que el lado restante, forman un revestimiento de El Cairo cuyos dos revestimientos hexagonales se pueden formar aplanando dos baldos perpendiculares por hexágonos regulares en direcciones perpendiculares, por una proporción de . Esta forma del azulejo de El Cairo hereda la propiedad de los azulejos por hexágonos regulares (sin cambios por el aplanamiento), que cada borde es collinear con infinitamente muchos otros bordes.
Azulejos con lados iguales
El pentágono regular no puede formar mosaicos de El Cairo, ya que no mosaico el plano sin espacios. Hay un pentágono equilátero único que puede formar un mosaico de El Cairo tipo 4; tiene cinco lados iguales pero sus ángulos son desiguales y su mosaico es bilateralmente simétrico. Una infinidad de otros pentágonos equiláteros pueden formar teselas de El Cairo de tipo 2.
Aplicaciones
Varias calles de El Cairo han sido pavimentadas con la forma colineal del mosaico de El Cairo; esta aplicación es el origen del nombre del mosaico. A partir de 2019, este patrón todavía se puede ver como decoración de superficie para azulejos cuadrados cerca del puente Qasr El Nil y la estación de metro El Behoos; Otras versiones del mosaico son visibles en otras partes de la ciudad. Algunos autores, incluido Martin Gardner, han escrito que este patrón se usa más ampliamente en la arquitectura islámica y, aunque esta afirmación parece haberse basado en un malentendido, en la Tumba de I'timād del siglo XVII se ven patrones que se asemejan a los azulejos de El Cairo. -ud-Daulah en la India, y el mosaico de El Cairo se ha encontrado en un jali mogol del siglo XVII.
- Tumba de I'timād-ud-Daulah, con paneles laterales rectangulares parecidos al azulejo de El Cairo
- Centar Zamet, con el azulejo de El Cairo visible en sus paredes
- El Cairo tiling in Hørsholm, Denmark
Una de las primeras publicaciones sobre los azulejos de El Cairo como patrón decorativo aparece en un libro sobre diseño textil de 1906. El inventor H. C. Moore presentó una patente estadounidense sobre los azulejos que forman este patrón en 1908. Aproximadamente al mismo tiempo, Villeroy & Boch creó una línea de baldosas cerámicas con el patrón de mosaico de El Cairo, utilizado en el vestíbulo del Laeiszhalle en Hamburgo, Alemania. Los azulejos de El Cairo se han utilizado como patrón decorativo en muchos diseños arquitectónicos recientes; por ejemplo, el centro de la ciudad de Hørsholm, Dinamarca, está pavimentado con este patrón, y el Centar Zamet, un pabellón deportivo en Croacia, lo utiliza tanto para sus paredes exteriores como para sus adoquines.
En cristalografía, este mosaico se ha estudiado al menos desde 1911. Se ha propuesto como estructura de cristales de hidrato en capas, ciertos compuestos de bismuto y hierro, y pentagrafeno, un compuesto hipotético de carbono puro. En la estructura del pentagrafeno, los bordes del mosaico que inciden en los vértices de grado cuatro forman enlaces simples, mientras que los bordes restantes forman enlaces dobles. En su forma hidrogenada, pentagrafano, todos los enlaces son enlaces simples y los átomos de carbono en los vértices de grado tres de la estructura tienen un cuarto enlace que los conecta con átomos de hidrógeno.
El mosaico de El Cairo ha sido descrito como uno de los "patrones geométricos favoritos" de M. C. Escher. Lo utilizó como base para su dibujo Conchas y estrellas de mar (1941), en el segmento de abejas sobre flores de su Metamorfosis III (1967-1968), y en varios otros dibujos de 1967-1968. Una imagen de este mosaico también se utilizó como portada de la primera edición de 1974 del libro de H. S. M. Coxeter Regular Complex Polytopes.