Momento dipolar magnético anómalo

En electrodinámica cuántica, el momento magnético anómalo de una partícula es una contribución de los efectos de la mecánica cuántica, expresados mediante diagramas de Feynman con bucles, al momento magnético de esa partícula. El momento magnético, también llamado momento dipolar magnético, es una medida de la fuerza de una fuente magnética.

El momento magnético "Dirac", correspondiente a los diagramas de Feynman a nivel de árboles (que se pueden considerar como el resultado clásico), se puede calcular a partir de la ecuación Dirac. Se expresa generalmente en términos del factor g; la ecuación Dirac predice g=2{displaystyle g=2}. Para partículas como el electrón, este resultado clásico difiere del valor observado por una pequeña fracción del porcentaje. La diferencia es el momento magnético anómalo, denotado a{displaystyle a} y definidas

a=g− − 22{displaystyle a={frac {}{2}}

Electrón

La contribución de un bucle al momento magnético anómalo (correspondiente a la primera y mayor corrección mecánica cuántica) del electrón se encuentra calculando la función de vértice que se muestra en el diagrama adyacente. El cálculo es relativamente sencillo  y el resultado de un bucle es:

ae=α α 2π π . . 0,0011614,{displaystyle a_{text{e}={frac} {Alpha}{2pi}approx 0,001,161,4,}

α α {displaystyle alpha }

α α 3{displaystyle alpha ^{3}

α α 5{displaystyle alpha ^{5}

ae=0,001159652181643()764){displaystyle a_{text{e}=0.001,159,652,181,643(764)}

La predicción QED concuerda con el valor medido experimentalmente en más de 10 cifras significativas, lo que convierte al momento magnético del electrón en una de las predicciones verificadas con mayor precisión en la historia de la física. (Consulte Pruebas de precisión de QED para obtener más detalles).

El valor experimental y la incertidumbre actuales son:

ae=0,00115965218059()13){displaystyle a_{text{e}=0.001,159,652,180,59(13)}

ae{displaystyle a_{text{e}}

g{displaystyle g}

Muón

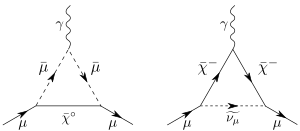
El momento magnético anómalo del muón se calcula de forma similar al del electrón. La predicción del valor del momento magnético anómalo del muón incluye tres partes:

aμ μ SM=aμ μ QED+aμ μ EW+aμ μ hadron=0,00116591804()51){displaystyle {begin{aligned}a_{mu} . {SM} }{mathrm {QED}+a_{mu} }{mathrm {EW}+a_{mu }{mathrm {hadron}\\=0.001,165,918,04(51)end{aligned}

De los dos primeros componentes, aμ μ QED{displaystyle a_{i} }{mathrm {QED} representa el fotón y los bucles de leptón, y aμ μ EW{displaystyle a_{i} . {EW} los bucles W boson, Higgs boson y Z boson; ambos se pueden calcular precisamente a partir de los primeros principios. El tercer mandato, aμ μ hadron{displaystyle a_{i} }{mathrm {hadron}, representa los lazos de hadron; no se puede calcular con precisión de la teoría sola. Se calcula a partir de mediciones experimentales de la proporción de secciones transversales hadrónicas a muónicas (R) en electron-antielectron (e⁻- E⁺Collisions. A partir de julio de 2017, la medición no está de acuerdo con el Modelo Estándar por 3.5 desviaciones estándar, sugiriendo que la física más allá del Modelo Estándar puede tener un efecto (o que los errores teóricos/experimentales no están completamente bajo control). Esta es una de las discrepancias de larga data entre el Modelo Estándar y el experimento.

El experimento E821 en el Laboratorio Nacional Brookhaven (BNL) estudió la precesión de muones y antimuones en un campo magnético externo constante mientras circulaban en un anillo de almacenamiento confinado. El experimento E821 informó el siguiente valor promedio

aμ μ =0,0011659209()6).{displaystyle a_{mu }=0.001;165;920;9(6). }

Un nuevo experimento en Fermilab llamado "Muon g−2" usando el imán E821 mejorará la precisión de este valor. Data taking comenzó en marzo de 2018 y se espera que termine en septiembre de 2022. Un resultado provisional liberado el 7 de abril de 2021 rendimientos aμ μ =0,00116592040()54){displaystyle a_{mu }=0.001,165,920,40(54)} que, en combinación con las mediciones existentes, da una estimación más precisa aμ μ =0,00116592061()41){displaystyle a_{mu }=0.001,165,920,61(41)}, superando la predicción Modelo Estándar por 4.2 desviaciones estándar. Además, el experimento E34 en J-PARC planea comenzar su primera carrera en 2024.

En abril de 2021, un grupo internacional de catorce físicos informó que mediante el uso de simulaciones de cromodinámica cuántica y electrodinámica cuántica ab-initio pudieron obtener una aproximación basada en la teoría que concordaba más con el valor experimental que con el valor basado en la teoría anterior. que se basó en los experimentos de aniquilación de electrones y positrones.

Tau

La predicción del modelo estándar para el momento dipolar magnético anómalo de tau es

aτ τ =0,00117721()5),{displaystyle a_{tau }=0.001,177,21(5),}

aτ τ {displaystyle a_{tau}}

Partículas compuestas

Las partículas compuestas suelen tener un enorme momento magnético anómalo. Los núcleos, protones y neutrones, ambos compuestos de quarks, son ejemplos. Los momentos magnéticos del núcleo son tanto grandes como inesperados; el momento magnético del protón es demasiado grande para una partícula elemental, mientras que se esperaba que el momento magnético del neutrón fuera cero debido a que su carga era cero.