Momento de inercia

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

El momento de inercia, también conocido como momento de inercia de masa, masa angular, segundo momento de masa o, más exactamente, inercia rotacional, de un cuerpo rígido es una cantidad que determina el par necesario para una aceleración angular deseada alrededor de un eje de rotación., similar a cómo la masa determina la fuerza necesaria para una aceleración deseada. Depende de la distribución de masa del cuerpo y del eje elegido, con momentos más grandes que requieren más torque para cambiar la velocidad de rotación del cuerpo.

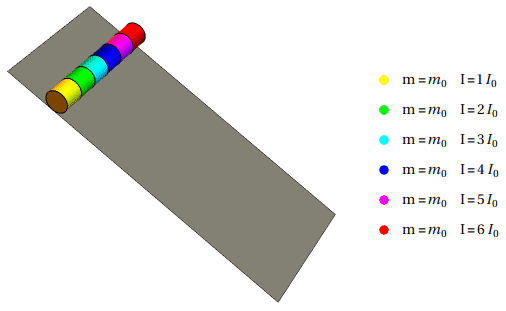
Es una propiedad extensiva (aditiva): para una masa puntual, el momento de inercia es simplemente la masa por el cuadrado de la distancia perpendicular al eje de rotación. El momento de inercia de un sistema compuesto rígido es la suma de los momentos de inercia de sus subsistemas componentes (todos tomados alrededor del mismo eje). Su definición más simple es el segundo momento de la masa con respecto a la distancia desde un eje.

Para cuerpos obligados a girar en un plano, solo importa su momento de inercia alrededor de un eje perpendicular al plano, un valor escalar. Para los cuerpos que giran libremente en tres dimensiones, sus momentos pueden describirse mediante una matriz simétrica de 3 × 3, con un conjunto de ejes principales mutuamente perpendiculares para los cuales esta matriz es diagonal y los pares alrededor de los ejes actúan independientemente unos de otros.

Introducción

Acróbata (Samuel Dixon) balanceándose sobre una cuerda, aprovechando el momento de inercia

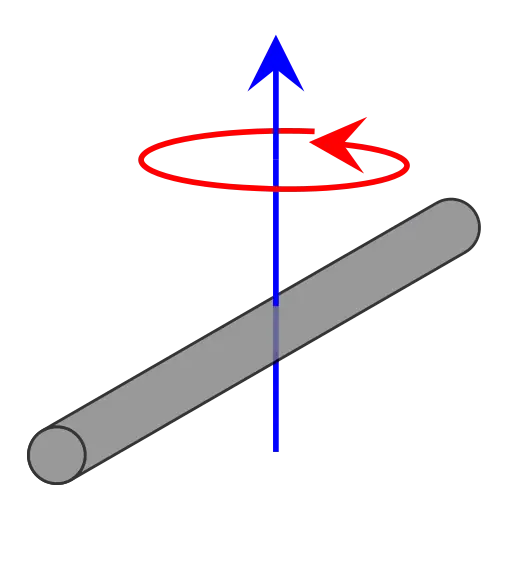
Cuando un cuerpo puede girar libremente alrededor de un eje, se debe aplicar un par para cambiar su momento angular. La cantidad de torque necesaria para causar cualquier aceleración angular dada (la tasa de cambio en la velocidad angular) es proporcional al momento de inercia del cuerpo. Los momentos de inercia pueden expresarse en unidades de kilogramo metro cuadrado (kg·m) en unidades SI y libra-pie-segundo cuadrado (lbf·ft·s) en unidades imperiales o estadounidenses.

El momento de inercia juega el papel en la cinética rotacional que la masa (inercia) juega en la cinética lineal; ambos caracterizan la resistencia de un cuerpo a los cambios en su movimiento. El momento de inercia depende de cómo se distribuya la masa alrededor de un eje de rotación y variará según el eje elegido. Para una masa puntual, el momento de inercia con respecto a algún eje viene dado por $señor^{2}$ , donde $r$ es la distancia del punto al eje y $metro$ es la masa. Para un cuerpo rígido extendido, el momento de inercia es simplemente la suma de todas las pequeñas piezas de masa multiplicada por el cuadrado de sus distancias desde el eje de rotación. Para un cuerpo extenso de forma regular y densidad uniforme, esta suma a veces produce una expresión simple que depende de las dimensiones, la forma y la masa total del objeto.

En 1673, Christiaan Huygens introdujo este parámetro en su estudio de la oscilación de un cuerpo que cuelga de un pivote, conocido como péndulo compuesto. El término momento de inercia fue introducido por Leonhard Euler en su libro Theoria motus corporum solidorum seu rigidorum en 1765, y se incorpora a la segunda ley de Euler.

La frecuencia natural de oscilación de un péndulo compuesto se obtiene de la relación entre el par impuesto por la gravedad sobre la masa del péndulo y la resistencia a la aceleración definida por el momento de inercia. La comparación de esta frecuencia natural con la de un péndulo simple que consta de un solo punto de masa proporciona una formulación matemática para el momento de inercia de un cuerpo extendido.

El momento de inercia también aparece en el momento, la energía cinética y en las leyes de movimiento de Newton para un cuerpo rígido como un parámetro físico que combina su forma y masa. Hay una diferencia interesante en la forma en que aparece el momento de inercia en el movimiento plano y espacial. El movimiento plano tiene un solo escalar que define el momento de inercia, mientras que para el movimiento espacial los mismos cálculos producen una matriz de momentos de inercia de 3 × 3, llamada matriz de inercia o tensor de inercia.

El momento de inercia de un volante giratorio se usa en una máquina para resistir variaciones en el par aplicado para suavizar su salida rotacional. El momento de inercia de un avión con respecto a sus ejes longitudinal, horizontal y vertical determina cómo las fuerzas de dirección en las superficies de control de sus alas, elevadores y timones afectan los movimientos del avión en balanceo, cabeceo y guiñada.

Definición

El momento de inercia se define como el producto de la masa de la sección y el cuadrado de la distancia entre el eje de referencia y el baricentro de la sección.

El momento de inercia I también se define como la relación entre el momento angular neto L de un sistema y su velocidad angular ω alrededor de un eje principal, es decir

Si el momento angular de un sistema es constante, a medida que el momento de inercia se hace más pequeño, la velocidad angular debe aumentar. Esto ocurre cuando los patinadores artísticos que giran tiran de sus brazos extendidos o los buzos enroscan sus cuerpos en una posición plegada durante una inmersión.

Si la forma del cuerpo no cambia, entonces su momento de inercia aparece en la ley de movimiento de Newton como la relación entre un par de torsión τ aplicado en un cuerpo y la aceleración angular α alrededor de un eje principal, es decir

{ estilo de visualización tau = I alfa.}

Para un péndulo simple, esta definición produce una fórmula para el momento de inercia I en términos de la masa m del péndulo y su distancia r desde el punto de pivote como,

Así, el momento de inercia del péndulo depende tanto de la masa m de un cuerpo como de su geometría, o forma, definida por la distancia r al eje de rotación.

Esta sencilla fórmula se generaliza para definir el momento de inercia de un cuerpo de forma arbitraria como la suma de todas las masas puntuales elementales dm, cada una multiplicada por el cuadrado de su distancia perpendicular r a un eje k. Por lo tanto, el momento de inercia de un objeto arbitrario depende de la distribución espacial de su masa.

En general, dado un objeto de masa m, se puede definir un radio efectivo k, dependiente de un eje de rotación particular, con un valor tal que su momento de inercia alrededor del eje es

donde k se conoce como el radio de giro alrededor del eje.

Ejemplos

Péndulo simple

Matemáticamente, el momento de inercia de un péndulo simple es la relación entre el par debido a la gravedad sobre el pivote de un péndulo y su aceleración angular sobre ese punto de pivote. Para un péndulo simple, se encuentra que es el producto de la masa de la partícula $metro$ por el cuadrado de su distancia $r$ al pivote, es decir

Esto se puede mostrar de la siguiente manera: La fuerza de la gravedad sobre la masa de un péndulo simple genera un momento de torsión ${displaystyle {boldsymbol {tau }}=mathbf {r} times mathbf {F} }$ alrededor del eje perpendicular al plano del movimiento del péndulo. Aquí $mathbf{r}$ está el vector de distancia desde el eje de torsión hasta el centro de masa del péndulo, y $mathbf {F}$ es la fuerza neta sobre la masa. Asociado con este momento de torsión hay una aceleración angular, ${ símbolo de negrita { alfa}}$ , de la cuerda y la masa alrededor de este eje. Dado que la masa está restringida a un círculo, la aceleración tangencial de la masa es ${displaystyle mathbf {a} ={boldsymbol {alpha}}times mathbf {r} }$ . Dado que ${displaystyle mathbf {F} =mmathbf {a} }$ la ecuación del par se convierte en:

{displaystyle {begin{alineado}{símbolo de bola {tau}}&=mathbf {r} times mathbf {F} =mathbf {r} times(m{símbolo de bola {alpha} } veces mathbf {r})\&=mleft(left(mathbf {r} cdot mathbf {r} right){símbolo de bola {alpha }}-left(mathbf {r} cdot {símbolo en negrita {alpha }}right)mathbf {r} right)\&=mr^{2}{símbolo en negrita {alpha }}=Ialpha mathbf { sombrero {k},end{alineado}}}

donde $mathbf{sombrero{k}}$ es un vector unitario perpendicular al plano del péndulo. (El penúltimo paso utiliza la expansión del producto triple vectorial con la perpendicularidad de ${ símbolo de negrita { alfa}}$ y $mathbf{r}$ ). La cantidad $yo=señor^{2}$ es el momento de inercia de esta masa única alrededor del punto de pivote.

La cantidad $yo=señor^{2}$ también aparece en el momento angular de un péndulo simple, que se calcula a partir de la velocidad ${displaystyle mathbf {v} ={boldsymbol {omega }}times mathbf {r} }$ de la masa del péndulo alrededor del pivote, donde ${ símbolo de negrita { omega}}$ es la velocidad angular de la masa alrededor del punto de pivote. Este momento angular está dado por

{displaystyle {begin{alineado}mathbf {L} &=mathbf {r} times mathbf {p} =mathbf {r} times left(m{símbolo de bola {omega}} veces mathbf {r} right)\&=mleft(left(mathbf {r} cdot mathbf {r} right){símbolo de bola {omega}}-left(mathbf {r} cdot {símbolo de bola {omega}}right)mathbf {r} right)\&=mr^{2}{símbolo de bola {omega}}=Iomega mathbf { sombrero {k }},end{alineado}}}

utilizando una derivación similar a la ecuación anterior.

De manera similar, la energía cinética de la masa del péndulo se define por la velocidad del péndulo alrededor del pivote para producir

{displaystyle E_{text{K}}={frac {1}{2}}mmathbf {v} cdot mathbf {v} ={frac {1}{2}}left(mr ^{2}right)omega ^{2}={frac {1}{2}}Iomega ^{2}.}

Esto muestra que la cantidad $yo=señor^{2}$ es cómo la masa se combina con la forma de un cuerpo para definir la inercia rotacional. El momento de inercia de un cuerpo de forma arbitraria es la suma de los valores $señor^{2}$ de todos los elementos de masa del cuerpo.

Péndulos compuestos

Los planeadores aprovechan su Momento de inercia en el aire

Un péndulo compuesto es un cuerpo formado por un conjunto de partículas de forma continua que gira rígidamente alrededor de un pivote. Su momento de inercia es la suma de los momentos de inercia de cada una de las partículas que lo componen. La frecuencia natural ( ${displaystyle omega_{text{n}}}$ ) de un péndulo compuesto depende de su momento de inercia, $yo_{p}$ ,

{displaystyle omega_{text{n}}={sqrt {frac {mgr}{I_{P}}}},}

donde $metro$ es la masa del objeto, $gramo$ es la aceleración local de la gravedad y $r$ es la distancia desde el punto de pivote hasta el centro de masa del objeto. La medición de esta frecuencia de oscilación en pequeños desplazamientos angulares proporciona una forma eficaz de medir el momento de inercia de un cuerpo.

Así, para determinar el momento de inercia del cuerpo, basta con suspenderlo de un punto de pivote conveniente $PAGS$ para que oscile libremente en un plano perpendicular a la dirección del momento de inercia deseado, luego medir su frecuencia natural o período de oscilación ( $t$ ), para obtener

{displaystyle I_{P}={frac {mgr}{omega_{text{n}}^{2}}}={frac {mgrt^{2}}{4pi ^{2} }},}

donde $t$ es el período (duración) de la oscilación (generalmente promediado durante múltiples períodos).

Centro de oscilación

Un péndulo simple que tiene la misma frecuencia natural que un péndulo compuesto define la longitud $L$ desde el pivote hasta un punto llamado centro de oscilación del péndulo compuesto. Este punto también corresponde al centro de percusión. La longitud $L$ se determina a partir de la fórmula,

{displaystyle omega_{text{n}}={sqrt {frac {g}{L}}}={sqrt {frac {mgr}{I_{P}}}},}

{displaystyle L={frac {g}{omega_{text{n}}^{2}}}={frac {I_{P}}{mr}}.}

El péndulo de segundos, que proporciona el "tick" y el "tac" de un reloj de pared, tarda un segundo en oscilar de lado a lado. Este es un período de dos segundos, o una frecuencia natural ${ estilo de visualización pi mathrm {rad/s}}$ del péndulo. En este caso, la distancia al centro de oscilación, $L$ , puede calcularse como

{displaystyle L={frac {g}{omega_{text{n}}^{2}}}approx {frac {9,81 mathrm {m/s^{2}} }{(3,14 mathrm {rad/s})^{2}}}aprox. 0,99 mathrm {m}.}

Observe que la distancia al centro de oscilación del péndulo de segundos debe ajustarse para acomodar diferentes valores para la aceleración local de la gravedad. El péndulo de Kater es un péndulo compuesto que usa esta propiedad para medir la aceleración local de la gravedad y se llama gravímetro.

Medición del momento de inercia

El momento de inercia de un sistema complejo, como un vehículo o un avión, alrededor de su eje vertical se puede medir suspendiendo el sistema de tres puntos para formar un péndulo trifilar. Un péndulo trifilar es una plataforma sostenida por tres alambres diseñados para oscilar en torsión alrededor de su eje centroidal vertical. El período de oscilación del péndulo trifilar da el momento de inercia del sistema.

Momento de inercia del área

El momento de inercia del área también se conoce como el segundo momento del área. Estos cálculos se utilizan comúnmente en ingeniería civil para el diseño estructural de vigas y columnas. Áreas de sección transversal calculadas para el momento vertical del eje x $yo_{{xx}}$ y el momento horizontal del eje y ${displaystyle I_{yy}}$ .La altura (h) y el ancho (b) son las medidas lineales, a excepción de los círculos, que se derivan efectivamente de la mitad del ancho, $r$

Momento de áreas seccionales calculado así

Cuadrado: ${displaystyle I_{xx}=I_{yy}={frac{b^{4}}{12}}}$
rectangulares: ${displaystyle I_{xx}={frac{bh^{3}}{12}}}$ y; ${displaystyle I_{aa}={frac{hb^{3}}{12}}}$
Triangular: ${displaystyle I_{xx}={frac{bh^{3}}{36}}}$
Circular: ${displaystyle I_{xx}=I_{yy}={frac {1}{4}}{pi }r^{4}}$

Movimiento en un plano fijo

Volante de inercia de una máquina de vapor de fábrica, su funcionamiento depende del punto del momento de inercia

Masa puntual

El momento de inercia alrededor de un eje de un cuerpo se calcula sumando $señor^{2}$ para cada partícula en el cuerpo, donde $r$ es la distancia perpendicular al eje especificado. Para ver cómo surge el momento de inercia en el estudio del movimiento de un cuerpo extendido, es conveniente considerar un conjunto rígido de masas puntuales. (Esta ecuación se puede usar para ejes que no son ejes principales siempre que se entienda que esto no describe completamente el momento de inercia).

Considere la energía cinética de un conjunto de $norte$ masas $mi}$ que se encuentran a las distancias $Rhode Island}$ del punto de pivote $PAGS$ , que es el punto más cercano en el eje de rotación. Es la suma de la energía cinética de las masas individuales,

{displaystyle E_{text{K}}=sum_{i=1}^{N}{frac {1}{2}},m_{i}mathbf {v}_{i} cdot mathbf {v} _{i}=sum _{i=1}^{N}{frac {1}{2}},m_{i}left(omega r_{i}right)^{2}={frac {1}{2}},omega ^{2}sum _{i=1}^{N}m_{i}r_{i}^{2}.}

Esto demuestra que el momento de inercia del cuerpo es la suma de cada uno de los $señor^{2}$ términos, es decir

{displaystyle I_{P}=sum_{i=1}^{N}m_{i}r_{i}^{2}.}

Así, el momento de inercia es una propiedad física que combina la masa y la distribución de las partículas alrededor del eje de rotación. Observe que la rotación sobre diferentes ejes del mismo cuerpo produce diferentes momentos de inercia.

El momento de inercia de un cuerpo continuo que gira alrededor de un eje específico se calcula de la misma manera, excepto que con un número infinito de partículas puntuales. Por lo tanto, se eliminan los límites de la suma, y la suma se escribe de la siguiente manera:

{displaystyle I_{P}=sum_{i}m_{i}r_{i}^{2}}

Otra expresión reemplaza la sumatoria con una integral,

{displaystyle I_{P}=iiint_{Q}rho(x,y,z)left|mathbf{r}right|^{2}dV}

Aquí, la función $rho$ da la densidad de masa en cada punto $(x, y, z)$ , $mathbf{r}$ es un vector perpendicular al eje de rotación y se extiende desde un punto en el eje de rotación hasta un punto $(x, y, z)$ en el sólido, y la integración se evalúa sobre el volumen $V$ del cuerpo $q$ . El momento de inercia de una superficie plana es similar con la densidad de masa reemplazada por su densidad de masa de área con la integral evaluada sobre su área.

Nota sobre el segundo momento de área: el momento de inercia de un cuerpo que se mueve en un plano y el segundo momento de área de la sección transversal de una viga se confunden a menudo. El momento de inercia de un cuerpo con la forma de la sección transversal es el segundo momento de esta área con respecto al $z$ eje perpendicular a la sección transversal, ponderado por su densidad. Esto también se llama el momento polar del área y es la suma de los segundos momentos con respecto a los ejes $X$ - y - $y$ . Las tensiones en una viga se calculan utilizando el segundo momento del área de la sección transversal alrededor del $X$ eje o del $y$ eje según la carga.

Ejemplos

El momento de inercia de un péndulo compuesto construido a partir de un disco delgado montado en el extremo de una varilla delgada que oscila alrededor de un pivote en el otro extremo de la varilla comienza con el cálculo del momento de inercia de la varilla delgada y el disco delgado. sobre sus respectivos centros de masa.

El momento de inercia de una barra delgada con sección transversal $s$ y densidad constantes $rho$ y con longitud $ana$ alrededor de un eje perpendicular que pasa por su centro de masa se determina por integración. Alinee el $X$ eje con la barra y ubique el origen de su centro de masa en el centro de la barra, luego ${displaystyle I_{C,{text{rod}}}=iiint _{Q}rho ,x^{2},dV=int _{-{frac {ell }{2}}}^{frac {ell }{2}}rho ,x^{2}s,dx=left.rho s{frac {x^{3}}{3}}right|_{-{frac {ell }{2}}}^{frac {ell }{2}}={frac {rho s}{3}}left({frac {ell ^{3}}{8}}+{frac {ell ^{3}}{8}}right)={frac {mell ^{2}}{12}},}$ donde ${displaystyle m=rho sell }$ es la masa de la barra.
El momento de inercia de un disco delgado $s$ de espesor, radio $R$ y densidad constantes $rho$ alrededor de un eje que pasa por su centro y es perpendicular a su cara (paralelo a su eje de simetría rotacional) se determina por integración. Alinee el $z$ eje - con el eje del disco y defina un elemento de volumen como ${displaystyle dV=sr,dr,dtheta}$ , luego ${displaystyle I_{C,{text{disco}}}=iiint _{Q}rho ,r^{2},dV=int _{0}^{2pi }int _ {0}^{R}rho r^{2}sr,dr,dtheta =2pi rho s{frac {R^{4}}{4}}={frac {1 {2}}mR^{2},}$ donde ${displaystyle m=pi R^{2}rho s}$ esta su masa.
El momento de inercia del péndulo compuesto ahora se obtiene sumando el momento de inercia de la barra y el disco alrededor del punto de pivote $PAGS$ como, ${displaystyle I_{P}=I_{C,{text{varilla}}}+M_{text{varilla}}left({frac {L}{2}}right)^{2}+ I_{C,{text{disco}}}+M_{text{disco}}(L+R)^{2},}$ donde $L$ es la longitud del péndulo. Observe que el teorema del eje paralelo se usa para cambiar el momento de inercia desde el centro de masa hasta el punto de pivote del péndulo.

Una lista de fórmulas de momentos de inercia para formas de cuerpo estándar proporciona una forma de obtener el momento de inercia de un cuerpo complejo como un conjunto de cuerpos con formas más simples. El teorema de los ejes paralelos se utiliza para desplazar el punto de referencia de los cuerpos individuales al punto de referencia del conjunto.

Como un ejemplo más, considere el momento de inercia de una esfera sólida de densidad constante alrededor de un eje que pasa por su centro de masa. Esto se determina sumando los momentos de inercia de los discos delgados que pueden formar la esfera cuyos centros están a lo largo del eje elegido para su consideración. Si la superficie de la pelota está definida por la ecuación

{ estilo de visualización x^{2}+y^{2}+z^{2}=R^{2},}

entonces el cuadrado del radio $r$ del disco en la sección transversal a $z$ lo largo del $z$ eje es

{displaystyle r(z)^{2}=x^{2}+y^{2}=R^{2}-z^{2}.}

Por lo tanto, el momento de inercia de la bola es la suma de los momentos de inercia de los discos a lo largo del $z$ eje,

{displaystyle {begin{alineado}I_{C,{text{bola}}}&=int _{-R}^{R}{frac {pi rho }{2}}r(z)^{4},dz=int _{-R}^{R}{frac {pi rho }{2}}left(R^{2}-z^{2}right) ^{2},dz\&={frac {pi rho }{2}}left[R^{4}z-{frac {2}{3}}R^{2}z ^{3}+{frac {1}{5}}z^{5}right]_{-R}^{R}\&=pi rho left(1-{frac {2 {3}}+{frac {1}{5}}right)R^{5}\&={frac {2}{5}}mR^{2},end{alineado}} }

donde ${textstyle m={frac {4}{3}}pi R^{3}rho }$ es la masa de la esfera.

Cuerpo rígido

Si un sistema mecánico está obligado a moverse en paralelo a un plano fijo, entonces la rotación de un cuerpo en el sistema ocurre alrededor de un eje $mathbf{sombrero{k}}$ perpendicular a este plano. En este caso, el momento de inercia de la masa en este sistema es un escalar conocido como momento polar de inercia. La definición del momento polar de inercia se puede obtener considerando el momento, la energía cinética y las leyes de Newton para el movimiento plano de un sistema rígido de partículas.

Si un sistema de $norte$ partículas, ${displaystyle P_{i},i=1,puntos,n}$ , se ensamblan en un cuerpo rígido, entonces el momento del sistema se puede escribir en términos de posiciones relativas a un punto de referencia $mathbf{R}$ y velocidades absolutas $mathbf {v} _{i}$ :

{displaystyle {begin{alineado}Delta mathbf{r}_{i}&=mathbf{r}_{i}-mathbf{R},\mathbf{v}_{i}& ={símbolo de bola {omega}}timesleft(mathbf{r}_{i}-mathbf{R}right)+mathbf{V} ={símbolo de bola {omega}}times Delta mathbf{r}_{i}+mathbf{V},end{alineado}}}

donde ${ símbolo de negrita { omega}}$ es la velocidad angular del sistema y $mathbf{V}$ es la velocidad de $mathbf{R}$ .

Para el movimiento plano, el vector de velocidad angular se dirige a lo largo del vector unitario $matemáticas {k}$ que es perpendicular al plano de movimiento. Introducir los vectores unitarios $mathbf {e} _{i}$ desde el punto de referencia $mathbf{R}$ hasta un punto $mathbf {r} _{i}$ , y el vector unitario ${displaystyle mathbf {hat {t}} _{i}=mathbf {hat {k}} times mathbf {hat {e}} _{i}}$ , de forma que

{displaystyle {begin{alineado}mathbf {hat {e}}_{i}&={frac {Delta mathbf {r}_{i}}{Delta r_{i}}}, quad mathbf {hat {k}} ={frac {símbolo de bola {omega}}{omega}},quad mathbf {hat {t}} _{i}=mathbf { hat {k}}timesmathbf{hat{e}}_{i},\mathbf{v}_{i}&={símbolo de bola {omega}}timesDeltamathbf{ r} _{i}+mathbf{V} =omegamathbf{hat{k}}timesDelta r_{i}mathbf{hat{e}} _{i}+mathbf{V } = omega,Delta r_{i}mathbf{hat{t}}_{i}+mathbf{V}end{alineado}}}

Esto define el vector de posición relativa y el vector de velocidad para el sistema rígido de las partículas que se mueven en un plano.

Nota sobre el producto cruz: Cuando un cuerpo se mueve paralelo a un plano de tierra, las trayectorias de todos los puntos del cuerpo se encuentran en planos paralelos a este plano de tierra. Esto significa que cualquier rotación que experimente el cuerpo debe ser alrededor de un eje perpendicular a este plano. El movimiento plano a menudo se presenta como proyectado sobre este plano de tierra, de modo que el eje de rotación aparece como un punto. En este caso, la velocidad angular y la aceleración angular del cuerpo son escalares y se ignora el hecho de que son vectores a lo largo del eje de rotación. Esto generalmente se prefiere para las introducciones al tema. Pero en el caso del momento de inercia, la combinación de masa y geometría se beneficia de las propiedades geométricas del producto vectorial. Por esta razón,

Momento angular

El vector de momento angular para el movimiento plano de un sistema rígido de partículas está dado por

{displaystyle {begin{alineado}mathbf{L}&=sum_{i=1}^{n}m_{i}Deltamathbf{r}_{i}timesmathbf{v} _ {i}\&=sum _{i=1}^{n}m_{i},Delta r_{i}mathbf {hat {e}} _{i}times left( omega,Delta r_{i}mathbf {hat {t}} _{i}+mathbf {V}right)\&=left(sum _{i=1}^{n } m_{i},Delta r_{i}^{2}right)omegamathbf{hat{k}} +left(sum_{i=1}^{n}m_{i },Delta r_{i}mathbf {hat {e}} _{i}right)times mathbf {V}.end{alineado}}}

Utilice el centro de masa $mathbf {C}$ como punto de referencia para que

{displaystyle {begin{alineado}Delta r_{i}mathbf {hat {e}}_{i}&=mathbf {r}_{i}-mathbf {C},\sum _{i=1}^{n}m_{i},Delta r_{i}mathbf {hat {e}}_{i}&=0,end{alineado}}}

y defina el momento de inercia relativo al centro de masa ${displaystyle I_{mathbf {C} }}$ como

{displaystyle I_{mathbf {C} }=sum_{i}m_{i},Delta r_{i}^{2},}

entonces la ecuación para el momento angular se simplifica a

{displaystyle mathbf {L} =I_{mathbf {C} }omega mathbf {hat {k}}.}

El momento de inercia ${displaystyle I_{mathbf {C} }}$ alrededor de un eje perpendicular al movimiento del sistema rígido y que pasa por el centro de masa se conoce como momento polar de inercia. Específicamente, es el segundo momento de masa con respecto a la distancia ortogonal a un eje (o polo).

Para una cantidad dada de momento angular, una disminución en el momento de inercia resulta en un aumento en la velocidad angular. Los patinadores artísticos pueden cambiar su momento de inercia tirando de sus brazos. Por lo tanto, la velocidad angular alcanzada por un patinador con los brazos extendidos da como resultado una mayor velocidad angular cuando los brazos se contraen, debido al momento de inercia reducido. Sin embargo, un patinador artístico no es un cuerpo rígido.

Energía cinética

La energía cinética de un sistema rígido de partículas que se mueven en el plano viene dada por

{displaystyle {begin{alineado}E_{text{K}}&={frac {1}{2}}sum _{i=1}^{n}m_{i}mathbf{v} _{i}cdot mathbf {v}_{i},\&={frac {1}{2}}sum_{i=1}^{n}m_{i}left( omega,Delta r_{i}mathbf{hat{t}}_{i}+mathbf{V}right)cdot left(omega,Delta r_{i}mathbf{ sombrero {t}}_{i}+mathbf{V}right),\&={frac{1}{2}}omega^{2}left(sum_{i=1} ^ {n}m_{i},Delta r_{i}^{2}mathbf {hat{t}} _{i}cdot mathbf{hat{t}} _{i}right) +omega mathbf {V} cdot left(sum _{i=1}^{n}m_{i},Delta r_{i}mathbf {hat {t}} _{i } right)+{frac {1}{2}}left(sum_{i=1}^{n}m_{i}right)mathbf{V}cdotmathbf{V} end{ alineado}}}

Sea el punto de referencia el centro de masa $mathbf {C}$ del sistema para que el segundo término se haga cero, e introduzca el momento de inercia ${displaystyle I_{mathbf {C} }}$ para que la energía cinética esté dada por

{displaystyle E_{text{K}}={frac{1}{2}}I_{mathbf{C}}omega^{2}+{frac{1}{2}}Mmathbf {V}cdotmathbf{V}.}

El momento de inercia ${displaystyle I_{mathbf {C} }}$ es el momento polar de inercia del cuerpo.

Leyes de newton

Las leyes de Newton para un sistema rígido de $norte$ partículas, ${displaystyle P_{i},i=1,puntos,n}$ , se pueden escribir en términos de una fuerza resultante y un momento de torsión en un punto de referencia $mathbf{R}$ , para producir

{displaystyle {begin{alineado}mathbf {F} &=sum _{i=1}^{n}m_{i}mathbf {A} _{i},\{boldsymbol {tau }}&=sum_{i=1}^{n}Delta mathbf {r}_{i}times m_{i}mathbf {A}_{i},end{alineado}}}

donde $mathbf {r} _{i}$ denota la trayectoria de cada partícula.

La cinemática de un cuerpo rígido produce la fórmula para la aceleración de la partícula $Pi}$ en términos de la posición $mathbf{R}$ y la aceleración $matemáticas {A}$ de la partícula de referencia, así como el vector de velocidad ${ símbolo de negrita { omega}}$ angular y el vector de aceleración angular ${ símbolo de negrita { alfa}}$ del sistema rígido de partículas como,

{displaystyle mathbf {A} _{i}={boldsymbol {alpha }}times Delta mathbf {r} _{i}+{boldsymbol {omega }}times {boldsymbol { omega }}times Delta mathbf {r} _{i}+mathbf {A}.}

Para los sistemas que están restringidos al movimiento plano, los vectores de velocidad angular y aceleración angular se dirigen $mathbf{sombrero{k}}$ perpendicularmente al plano de movimiento, lo que simplifica esta ecuación de aceleración. En este caso, los vectores de aceleración se pueden simplificar introduciendo los vectores unitarios ${ estilo de visualización mathbf { sombrero {e}} _ {i}}$ del punto de referencia $mathbf{R}$ a un punto $mathbf {r} _{i}$ y los vectores unitarios ${displaystyle mathbf {hat {t}} _{i}=mathbf {hat {k}} times mathbf {hat {e}} _{i}}$ , por lo que

{displaystyle {begin{alineado}mathbf{A}_{i}&=alphamathbf{hat{k}}timesDelta r_{i}mathbf{hat{e}}_{ i}-omegamathbf{hat{k}}timesomegamathbf{hat{k}}timesdelta r_{i}mathbf{hat{e}}_{i}+ mathbf{A}\&=alphaDelta r_{i}mathbf{hat{t}}_{i}-omega^{2}Delta r_{i}mathbf{hat{e} } _{i}+mathbf{A}.end{alineado}}}

Esto produce el par resultante en el sistema como

{displaystyle {begin{alineado}{símbolo de bola {tau}}&=sum _{i=1}^{n}m_{i},Delta r_{i}mathbf {hat { e }} _{i}times left(alpha Delta r_{i}mathbf {hat {t}} _{i}-omega ^{2}Delta r_{i}mathbf { sombrero {e}} _{i}+mathbf {A}right)\&=left(sum_{i=1}^{n}m_{i},Delta r_{i}^{ 2}right)alpha mathbf {hat {k}} +left(sum _{i=1}^{n}m_{i},Delta r_{i}mathbf {hat { e}} _{i}right)timesmathbf{A},end{alineado}}}

donde ${displaystyle mathbf {hat {e}} _ {i}times mathbf {hat {e}}_{i}=mathbf {0} }$ , y ${displaystyle mathbf {hat {e}} _{i}times mathbf {hat {t}} _{i}=mathbf {hat {k}} }$ es el vector unitario perpendicular al plano para todas las partículas $Pi}$ .

Use el centro de masa $mathbf {C}$ como punto de referencia y defina el momento de inercia relativo al centro de masa ${displaystyle I_{mathbf {C} }}$ , luego la ecuación para el par resultante se simplifica a

{displaystyle {boldsymbol {tau }}=I_{mathbf {C} }alpha mathbf {hat {k}}.}

Movimiento en el espacio de un cuerpo rígido y la matriz de inercia

Los momentos escalares de inercia aparecen como elementos en una matriz cuando un sistema de partículas se ensambla en un cuerpo rígido que se mueve en un espacio tridimensional. Esta matriz de inercia aparece en el cálculo del momento angular, la energía cinética y el par resultante del sistema rígido de partículas.

Deje que el sistema de $norte$ partículas ${displaystyle P_{i},i=1,puntos,n}$ se ubique en las coordenadas $mathbf {r} _{i}$ con velocidades $mathbf {v} _{i}$ relativas a un marco de referencia fijo. Para un punto de referencia (posiblemente en movimiento) $mathbf{R}$ , las posiciones relativas son

{displaystyle Delta mathbf {r} _{i}=mathbf {r} _{i}-mathbf {R} }

y las velocidades (absolutas) son

{displaystyle mathbf {v} _{i}={boldsymbol {omega }}times Delta mathbf {r} _{i}+mathbf {V}_{mathbf {R} }}

donde ${ símbolo de negrita { omega}}$ es la velocidad angular del sistema, y ${displaystyle mathbf {V_{R}} }$ es la velocidad de $mathbf{R}$ .

Momento angular

Tenga en cuenta que el producto cruzado se puede escribir de manera equivalente como una multiplicación de matrices combinando el primer operando y el operador en una matriz asimétrica ${displaystyle left[mathbf {b} right]}$ , construida a partir de los componentes de ${displaystyle mathbf {b} =(b_{x},b_{y},b_{z})}$ :

{displaystyle {begin{alineado}mathbf{b}timesmathbf{y}&equivleft[mathbf{b}right]mathbf{y}\left[mathbf{b} right]&equiv {begin{bmatriz}0&-b_{z}&b_{y}\b_{z}&0&-b_{x}\-b_{y}&b_{x}&0end{bmatriz }}.end{alineado}}}

La matriz de inercia se construye considerando el momento angular, con el punto $mathbf{R}$ de referencia del cuerpo elegido como centro de masa $mathbf {C}$ :

{displaystyle {begin{alineado}mathbf{L}&=sum_{i=1}^{n}m_{i},Deltamathbf{r}_{i}timesmathbf{ v } _{i}\&=sum _{i=1}^{n}m_{i},Delta mathbf {r} _{i}times left({símbolo de bola {omega }}timesDeltamathbf{r}_{i}+mathbf{V}_{mathbf{R}}right)\&=left(-sum _{i=1}^{ n}m_{i},Deltamathbf{r}_{i}timesleft(Deltamathbf{r}_{i}times{ballsymbol {omega}}right)right)+left(sum_{i=1}^{n}m_{i},Deltamathbf{r}_{i}timesmathbf{V}_{mathbf{R}} derecha),end{alineado}}}

donde los términos que contienen ${displaystyle mathbf {V_{R}} }$ ( ${displaystyle =mathbf {C} }$ ) suman cero por la definición del centro de masa.

Entonces, la matriz simétrica sesgada ${ estilo de visualización [ Delta mathbf {r} _ {i}]}$ obtenida del vector de posición relativa ${displaystyle Delta mathbf {r} _{i}=mathbf {r} _{i}-mathbf {C} }$ , se puede usar para definir,

{displaystyle mathbf {L} =left(-sum _{i=1}^{n}m_{i}left[Delta mathbf {r}_{i}right]^{2} right){boldsymbol {omega }}=mathbf {I} _{mathbf {C} }{boldsymbol {omega }},}

donde ${displaystyle mathbf {I_{C}} }$ definido por

{displaystyle mathbf {I}_{mathbf {C} }=-sum_{i=1}^{n}m_{i}left[Delta mathbf {r}_{i}right ]^{2},}

es la matriz de inercia simétrica del sistema rígido de partículas medida con respecto al centro de masa $mathbf {C}$ .

Energía cinética

La energía cinética de un sistema rígido de partículas se puede formular en términos del centro de masa y una matriz de momentos de inercia de masa del sistema. Si el sistema de $norte$ partículas ${displaystyle P_{i},i=1,puntos,n}$ se ubica en las coordenadas $mathbf {r} _{i}$ con velocidades $mathbf {v} _{i}$ , entonces la energía cinética es

{displaystyle E_{text{K}}={frac {1}{2}}sum_{i=1}^{n}m_{i}mathbf{v}_{i}cdot mathbf {v}_{i}={frac {1}{2}}sum _{i=1}^{n}m_{i}left({símbolo de bola {omega}}times Delta mathbf{r}_{i}+mathbf{V}_{mathbf{C}}right)cdotleft({ballsymbol{omega}}timesDeltamathbf{r}_{ i}+mathbf{V}_{mathbf{C}}derecha),}

donde ${displaystyle Delta mathbf {r} _{i}=mathbf {r} _{i}-mathbf {C} }$ es el vector de posición de una partícula con respecto al centro de masa.

Esta ecuación se expande para producir tres términos

{displaystyle E_{text{K}}={frac {1}{2}}left(sum _{i=1}^{n}m_{i}left({símbolo de bola { omega }}timesDeltamathbf{r}_{i}right)cdotleft({símbolo en negrita {omega}}timesDeltamathbf{r}_{i}right) derecha) +left(sum_{i=1}^{n}m_{i}mathbf {V}_{mathbf {C} }cdot left({símbolo de bola {omega }} veces Delta mathbf{r}_{i}right)right)+{frac{1}{2}}left(sum_{i=1}^{n}m_{i}mathbf{ V} _ {mathbf{C}}cdot mathbf{V}_{mathbf{C}}right).}

El segundo término en esta ecuación es cero porque $mathbf {C}$ es el centro de masa. Introduzca la matriz simétrica oblicua ${ estilo de visualización [ Delta mathbf {r} _ {i}]}$ para que la energía cinética se convierta en

{displaystyle {begin{alineado}E_{text{K}}&={frac {1}{2}}left(sum_{i=1}^{n}m_{i}left (left[Deltamathbf {r}_{i}right]{símbolo de bola {omega}}right)cdot left(left[Deltamathbf{r}_{i} derecha]{símbolo de bola {omega}}derecha)derecha)+{frac {1}{2}}izquierda(sum_{i=1}^{n}m_{i}derecha) mathbf {V}_{mathbf {C}}cdot mathbf {V}_{mathbf {C}}\&={frac {1}{2}}left(sum_{i =1 }^{n}m_{i}left({símbolo de bola {omega}}^{mathsf {T}}left[Deltamathbf {r}_{i}right]^{ mathsf { T}}left[Deltamathbf {r}_{i}right]{ballsymbol {omega}}right)right)+{frac {1}{2}}left (sum _{i=1}^{n}m_{i}right)mathbf{V}_{mathbf{C}}cdot mathbf{V}_{mathbf{C}}\ &={frac {1}{2}}{símbolo de bola {omega}}cdot left(-sum _{i=1}^{n}m_{i}left[Delta mathbf { r } _{i}right]^{2}right){símbolo de bola {omega}}+{frac {1}{2}}left(sum_{i=1}^{n }m_ {i}right)mathbf{V}_{mathbf{C}}cdot mathbf{V}_{mathbf{C}}.end{alineado}}}

Así, la energía cinética del sistema rígido de partículas viene dada por

{displaystyle E_{text{K}}={frac {1}{2}}{boldsymbol {omega }}cdot mathbf {I}_{mathbf {C} }{boldsymbol { omega }}+{frac {1}{2}}Mmathbf {V}_{mathbf {C} }^{2}.}

donde ${displaystyle mathbf {I_{C}} }$ es la matriz de inercia relativa al centro de masa y $METRO$ es la masa total.

Par resultante

La matriz de inercia aparece en la aplicación de la segunda ley de Newton a un conjunto rígido de partículas. El par resultante en este sistema es,

{displaystyle {boldsymbol {tau }}=sum _{i=1}^{n}left(mathbf {r_{i}} -mathbf {R} right)times m_{i} mathbf {a} _{i},}

donde $mathbf{a}_i$ es la aceleración de la partícula $Pi}$ . La cinemática de un cuerpo rígido produce la fórmula para la aceleración de la partícula $Pi}$ en términos de la posición $mathbf{R}$ y la aceleración ${ estilo de visualización mathbf {A} _ { mathbf {R}}}$ del punto de referencia, así como el vector de velocidad ${ símbolo de negrita { omega}}$ angular y el vector de aceleración angular ${ símbolo de negrita { alfa}}$ del sistema rígido como,

{displaystyle mathbf {a} _{i}={boldsymbol {alpha }}times left(mathbf {r} _{i}-mathbf {R} right)+{boldsymbol { omega }}times left({boldsymbol {omega }}times left(mathbf {r}_{i}-mathbf {R} right)right)+mathbf {A}_{ mathbf{R} }.}

Use el centro de masa $mathbf {C}$ como punto de referencia e introduzca la matriz simétrica oblicua ${displaystyle left[Delta mathbf {r} _{i}right]=left[mathbf {r} _{i}-mathbf {C} right]}$ para representar el producto vectorial ${ estilo de visualización ( mathbf {r} _ {i}- mathbf {C}) veces}$ , para obtener

{displaystyle {boldsymbol {tau }}=left(-sum_{i=1}^{n}m_{i}left[Delta mathbf {r}_{i}right]^ {2}right){boldsymbol {alpha }}+{boldsymbol {omega }}times left(-sum _{i=1}^{n}m_{i}left[Delta mathbf {r} _{i}right]^{2}right){boldsymbol {omega }}}

El cálculo utiliza la identidad

{displaystyle Delta mathbf {r} _{i}times left({boldsymbol {omega }}times left({boldsymbol {omega }}times Delta mathbf {r} _ {i}right)right)+{boldsymbol {omega }}times left(left({boldsymbol {omega }}times Delta mathbf {r}_{i}right) times Delta mathbf {r} _{i}right)=0,}

obtenido de la identidad de Jacobi para el producto cruzado triple como se muestra en la siguiente prueba:

Prueba

{displaystyle {begin{alineado}{boldsymbol {tau }}&=sum _{i=1}^{n}(mathbf {r_{i}} -mathbf {R})times (m_{i}mathbf {a} _{i})\&=sum _{i=1}^{n}{boldsymbol {Delta}}mathbf {r}_{i}times (m_{i}mathbf {a} _{i})\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{ i}times mathbf {a} _{i}];ldots {text{multiplicación escalar de productos cruzados}}\&=sum _{i=1}^{n}m_{i}[ {boldsymbol {Delta }}mathbf {r}_{i}times (mathbf {a}_{{text{tangencial}},i}+mathbf {a}_{text{centrípeta }},i}+mathbf {A} _{mathbf {R} })]\&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }} mathbf {r} _{i}times (mathbf {a} _ {{text{tangencial}},i}+mathbf {a}_{{text{centrípeta}},i}+0) ]\&;;;;;ldots ;mathbf {R} {text{ está en reposo o moviéndose a una velocidad constante pero no acelerada, o }}\&;;;;;;;;;;;{text{el origen del sistema de referencia de coordenadas (mundiales) fijo se coloca en el centro de masa }}mathbf {C} \&=sum _{i=1}^{n}m_{i}[ {boldsymbol {Delta}}mathbf {r}_{i}times mathbf {a}_{text{tangencial}},i}+{boldsymbol {Delta}}mathbf {r} _ {i}times mathbf {a}_{{text{centrípeta}},i}];ldots {text{ distributividad de productos cruzados sobre la suma}}\&=sum_{i= 1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }} mathbf {r} _{i})+{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times mathbf {v}_{text {tangencial}},i})]\{boldsymbol {tau }}&=sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {alpha}}times { boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({ boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))]\end{alineado}}}

Entonces, se usa la siguiente identidad de Jacobi en el último término:

{displaystyle {begin{alineado}0&={boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }} times {boldsymbol {Delta }}mathbf {r} _{i}))+{boldsymbol {omega }}times (({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})times {boldsymbol {Delta }}mathbf {r} _{i})+({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {omega }})\&={boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }} mathbf {r} _{i}))+{boldsymbol {omega }}times (({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r}_{i })times {boldsymbol {Delta }}mathbf {r} _{i})+({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r}_{i })times -({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i});ldots {text{ anticonmutatividad de productos cruzados}}\ &={boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }} mathbf {r} _{i}))+{boldsymbol {omega }}times (({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r}_{i })times {boldsymbol {Delta }}mathbf {r} _{i})+-[({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _ {i})times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})];ldots {text{multiplicación escalar de productos cruzados} }\&={boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol { Delta }}mathbf {r} _{i}))+{boldsymbol {omega }}times (({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r } _{i})times {boldsymbol {Delta }}mathbf {r} _{i})+-[0];ldots {text{ autoproducto cruzado}}\0&={boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))+{boldsymbol {omega }}times (({boldsymbol {omega }}times { boldsymbol {Delta }}mathbf {r} _{i})times {boldsymbol {Delta }}mathbf {r} _{i})end{alineado}}}

El resultado de aplicar la identidad de Jacobi se puede continuar de la siguiente manera:

{displaystyle {begin{alineado}{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))&=-[{boldsymbol {omega }}times (({boldsymbol {omega }}times {boldsymbol { Delta }}mathbf {r} _{i})times {boldsymbol {Delta }}mathbf {r} _{i})]\&=-[({boldsymbol {omega }} times {boldsymbol {Delta}}mathbf {r} _{i})({boldsymbol {omega}}cdot {boldsymbol {Delta}}mathbf {r} _{i})-{ boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {omega }}cdot ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r } _{i}))];ldots {text{producto triple vectorial}}\&=-[({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})({boldsymbol {omega }}cdot {boldsymbol {Delta } }mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r}_{i}cdot ({boldsymbol {omega }}times {boldsymbol {omega }}))];ldots {text{producto triple escalar}}\&=-[({boldsymbol {omega }} times {boldsymbol {Delta}}mathbf {r} _{i})({boldsymbol {omega}}cdot {boldsymbol {Delta}}mathbf {r} _{i})-{ boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot (0))];ldots {text{ self producto cruzado}}\&=-[({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _{i})({boldsymbol {omega }} cdot {boldsymbol {Delta}}mathbf {r} _{i})]\&=-[{boldsymbol {omega}}times ({boldsymbol {Delta}}mathbf {r}_{i}({boldsymbol {omega}}cdot {boldsymbol {Delta}} mathbf {r} _{i}))];ldots {text{ multiplicación escalar de productos cruzados}}\&={boldsymbol {omega }}times -({boldsymbol {Delta } }mathbf {r}_{i}({boldsymbol {omega }}cdot {boldsymbol {Delta }}mathbf {r}_{i}));ldots {text{ cruz- multiplicación escalar del producto}}\{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times { boldsymbol {Delta }}mathbf {r} _{i}))&={boldsymbol {omega }}times -({boldsymbol {Delta }}mathbf {r} _{i}({ boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }}));ldots {text{conmutatividad punto-producto}}\end{alineado}} }ldots {text{multiplicación escalar de productos cruzados}}\&={boldsymbol {omega }}times -({boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {omega }}cdot {boldsymbol {Delta }}mathbf {r} _{i}));ldots {text{multiplicación escalar de productos cruzados}}\{boldsymbol {Delta } }mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r}_{i }))&={boldsymbol {omega }}times -({boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r}_{ i}cdot {boldsymbol {omega }}));ldots {text{conmutatividad punto-producto}}\end{alineado}}}ldots {text{multiplicación escalar de productos cruzados}}\&={boldsymbol {omega }}times -({boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {omega }}cdot {boldsymbol {Delta }}mathbf {r} _{i}));ldots {text{multiplicación escalar de productos cruzados}}\{boldsymbol {Delta } }mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r}_{i }))&={boldsymbol {omega }}times -({boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r}_{ i}cdot {boldsymbol {omega }}));ldots {text{conmutatividad punto-producto}}\end{alineado}}}ldots {text{multiplicación escalar de productos cruzados}}\{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol { omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))&={boldsymbol {omega }}times -({boldsymbol {Delta }}mathbf { r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }}));ldots {text{conmutatividad del producto escalar}} \end{alineado}}}ldots {text{multiplicación escalar de productos cruzados}}\{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times ({boldsymbol { omega }}times {boldsymbol {Delta }}mathbf {r} _{i}))&={boldsymbol {omega }}times -({boldsymbol {Delta }}mathbf { r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }}));ldots {text{conmutatividad del producto escalar}} \end{alineado}}}

El resultado final se puede sustituir por la prueba principal de la siguiente manera:

{displaystyle {begin{alineado}{boldsymbol {tau }}&=sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _ {i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {Delta }}mathbf {r}_{ i}times ({boldsymbol {omega }}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r}_{i}))]\&= sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times -({boldsymbol {Delta }}mathbf {r}_{i}({boldsymbol { Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }}))]\&=sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {alpha}}times { boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {0-{boldsymbol {Delta }}mathbf {r} _{i}({ boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})}]\&=sum _{i=1}^{n}m_{i} [{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {alpha}}times {boldsymbol {Delta}}mathbf {r}_{i})+ {boldsymbol {omega }}times {[{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }} mathbf {r} _{i})-{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r } _{i})]-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol { omega }})}];ldots;{boldsymbol {omega}}({boldsymbol {Delta}}mathbf {r}_{i}cdot {boldsymbol {Delta}}mathbf {r}_{i})-{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})=0\&= sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol { Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {[{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _ {i}cdot {boldsymbol {Delta}}mathbf {r}_{i})-{boldsymbol {Delta}}mathbf {r}_{i}({boldsymbol {Delta} }mathbf {r} _{i}cdot {boldsymbol {omega }})]-{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r} _{i} cdot {boldsymbol {Delta }}mathbf {r} _{i})}];ldots {text{ suma asociatividad}}\end{alineado}}}ldots {text{ suma asociatividad}}\end{alineado}}}ldots {text{ suma asociatividad}}\end{alineado}}}ldots {text{ suma asociatividad}}\end{alineado}}}ldots {text{ suma asociatividad}}\end{alineado}}}=sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {alpha}}times { boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {[{boldsymbol {omega }}({boldsymbol {Delta }}mathbf { r}_{i}cdot {boldsymbol {Delta}}mathbf {r}_{i})-{boldsymbol {Delta}}mathbf {r}_{i}({boldsymbol { Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})]-{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r}_{i }cdot {boldsymbol {Delta }}mathbf {r} _{i})}];ldots {text{ asociatividad adicional}}\end{alineado}}}=sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {alpha}}times { boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {[{boldsymbol {omega }}({boldsymbol {Delta }}mathbf { r}_{i}cdot {boldsymbol {Delta}}mathbf {r}_{i})-{boldsymbol {Delta}}mathbf {r}_{i}({boldsymbol { Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})]-{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r}_{i }cdot {boldsymbol {Delta }}mathbf {r} _{i})}];ldots {text{ asociatividad adicional}}\end{alineado}}}ldots {text{ suma asociatividad}}\end{alineado}}}ldots {text{ suma asociatividad}}\end{alineado}}}

{displaystyle {begin{alineado}&=sum_{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r}_{i}times ({ boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {{boldsymbol {omega }}({ boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _ {i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})}-{boldsymbol {omega }}times {boldsymbol { omega }}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})];ldots {text{ distributividad entre productos sobre la suma}}\&=sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {alpha}}times { boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r } _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})}-({boldsymbol {Delta }}mathbf {r}_{i}cdot {boldsymbol { Delta }}mathbf {r} _{i})({boldsymbol {omega }}times {boldsymbol {omega }})];ldots {text{multiplicación escalar de productos cruzados}} &=sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {alpha}}times { boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r } _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})}-({boldsymbol {Delta }}mathbf {r}_{i}cdot {boldsymbol { Delta }}mathbf {r} _{i})(0)];ldots {text{ autoproducto cruzado}}\&=sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {alpha}}times { boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol {omega }}times {{boldsymbol {omega }}({boldsymbol {Delta }}mathbf {r } _{i}cdot {boldsymbol {Delta }}mathbf {r} _{i})-{boldsymbol {Delta }}mathbf {r} _{i}({boldsymbol {Delta }}mathbf {r} _{i}cdot {boldsymbol {omega }})}]\&=sum _{i=1}^{n}m_{i}[{boldsymbol { Delta }}mathbf {r} _{i}times ({boldsymbol {alpha }}times {boldsymbol {Delta }}mathbf {r} _{i})+{boldsymbol { omega }}times {{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {omega }}times {boldsymbol {Delta }}mathbf {r} _ {i})}];ldots {text{producto triple vectorial}}\&=sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times -({boldsymbol {Delta}}mathbf { r} _ {i}times {boldsymbol {alpha }})+{boldsymbol {omega }}times {{boldsymbol {Delta }}mathbf {r}_{i}times - ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {omega }})}];ldots {text{ anticonmutatividad de productos cruzados}}\&= -sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {Delta}}mathbf {r } _ {i}times {boldsymbol {alpha }})+{boldsymbol {omega }}times {{boldsymbol {Delta }}mathbf {r}_{i}times ({ boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {omega }})}];ldots {text{multiplicación escalar de productos cruzados}}\&=-sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {Delta}}mathbf { r} _{i}times {boldsymbol {alpha }})]+-sum _{i=1}^{n}m_{i}[{boldsymbol {omega }}times {{ boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {omega }})}] ;ldots {text{ suma distributividad}}\{boldsymbol {tau }}&=-sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }} mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {alpha }})]+{boldsymbol {omega }} times -sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times {boldsymbol {omega }})];ldots ;{boldsymbol {omega }}{text{ no es característico de la partícula }}P_{i}end {alineado}}}{boldsymbol {omega }}{text{ no es característico de la partícula }}P_{i}end{aligned}}}{boldsymbol {omega }}{text{ no es característico de la partícula }}P_{i}end{aligned}}}ldots {text{ distributividad de suma}}\{boldsymbol {tau }}&=-sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _ {i}times ({boldsymbol {Delta }}mathbf {r}_{i}times {boldsymbol {alpha }})]+{boldsymbol {omega }}times -sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {Delta}}mathbf {r } _{i}times {boldsymbol {omega }})];ldots ;{boldsymbol {omega }}{text{ no es característico de la partícula }}P_{i}end{alineada }}}ldots {text{ distributividad de suma}}\{boldsymbol {tau }}&=-sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _ {i}times ({boldsymbol {Delta }}mathbf {r}_{i}times {boldsymbol {alpha }})]+{boldsymbol {omega }}times -sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {Delta}}mathbf {r } _{i}times {boldsymbol {omega }})];ldots ;{boldsymbol {omega }}{text{ no es característico de la partícula }}P_{i}end{alineada }}}{boldsymbol {omega }}{text{ no es característico de la partícula }}P_{i}end{aligned}}}{boldsymbol {omega }}{text{ no es característico de la partícula }}P_{i}end{aligned}}}

Observe que para cualquier vector $mathbf{u}$ , se cumple lo siguiente:

{displaystyle {begin{alineado}-sum_{i=1}^{n}m_{i}[{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {Delta }}mathbf {r} _{i}times mathbf {u})]&=-sum _{i=1}^{n}m_{i}left({begin{bmatrix }0&-Delta r_{3,i}&Delta r_{2,i}\Delta r_{3,i}&0&-Delta r_{1,i}\-Delta r_{2,i }&Delta r_{1,i}&0end{bmatrix}}left({begin{bmatrix}0&-Delta r_{3,i}&Delta r_{2,i}\Delta r_ {3,i}&0&-Delta r_{1,i}\-Delta r_{2,i}&Delta r_{1,i}&0end{bmatriz}}{begin{bmatriz}u_{ 1}\u_{2}\u_{3}end{bmatrix}}right)right);ldots {text{ producto cruzado como multiplicación de matrices}}\[6pt]&=- sum _{i=1}^{n}m_{i}left({begin{bmatrix}0&-Delta r_{3,i}&Delta r_{2,i}\Delta r_{ 3,i}&0&-Delta r_{1,i}\-Delta r_{2,i}&Delta r_{1,i}&0end{bmatriz}}{begin{bmatriz}-Delta r_{3,i},u_{2}+Delta r_{2,i},u_{3}\+Delta r_{3,i},u_{1}-Delta r_{1,i},u_{3 }\-Delta r_{2,i},u_{1}+Delta r_{1,i},u_{2}end{bmatrix}}right)\[6pt]&=- sum _{i=1}^{n}m_{i}{begin{bmatriz}-Delta r_{3,i}(+Delta r_{3,i},u_{1}-Delta r_{1,i},u_{3})+Delta r_{2,i}(-Delta r_{2,i},u_{1}+Delta r_{1,i},u_ {2})\+Delta r_{3,i}(-Delta r_{3,i},u_{2}+Delta r_{2,i},u_{3})-Delta r_{1,i}(-Delta r_{2,i},u_{1}+Delta r_{1,i},u_{2})\-Delta r_{2,i}(-Delta r_{3,i},u_{2}+Delta r_{2,i},u_{3})+Delta r_{1,i}(+Delta r_{3,i} ,u_{1}-Delta r_{1,i},u_{3})end{bmatrix}}\[6pt]&=-sum _{i=1}^{n}m_{ i}{begin{bmatriz}-Delta r_{3,i}^{2},u_{1}+Delta r_{1,i}Delta r_{3,i},u_{3} -Delta r_{2,i}^{2},u_{1}+Delta r_{1,i}Delta r_{2,i},u_{2}\-Delta r_{3,i}^{2},u_{2}+Delta r_{2,i}Delta r_{3,i},u_{3}+Delta r_{2,i}Delta r_{1,i},u_{1}-Delta r_{1,i}^{2},u_{2}\+Delta r_{3,i}Delta r_{2,i},u_{2}- Delta r_{2,i}^{2},u_{3}+Delta r_{3,i}Delta r_{1,i},u_{1}-Delta r_{1,i}^ {2},u_{3}end{bmatrix}}\[6pt]&=-sum _{i=1}^{n}m_{i}{begin{bmatrix}-(Delta r_ {2,i}^{2}+Delta r_{3,i}^{2}),u_{1}+Delta r_{1,i}Delta r_{2,i},u_{ 2}+Delta r_{1,i}Delta r_{3,i},u_{3}\+Delta r_{2,i}Delta r_{1,i},u_{1} -(Delta r_{1,i}^{2}+Delta r_{3,i}^{2}),u_{2}+Delta r_{2,i}Delta r_{3,i },u_{3}\+Delta r_{3,i}Delta r_{1,i},u_{1}+Delta r_{3,i}Delta r_{2,i},u_{2}-(Delta r_{1,i}^{2}+Delta r_{2,i}^{2}),u_{3}end{bmatriz}}\[6pt] &=-sum _{i=1}^{n}m_{i}{begin{bmatriz}-(Delta r_{2,i}^{2}+Delta r_{3,i}^{ 2})&Delta r_{1,i}Delta r_{2,i}&Delta r_{1,i}Delta r_{3,i}\Delta r_{2,i}Delta r_ {1,i}&-(Delta r_{1,i}^{2}+Delta r_{3,i}^{2})&Delta r_{2,i}Delta r_{3,i}\Delta r_{3,i}Delta r_{1,i}&Delta r_{3,i}Delta r_{2,i}&-(Delta r_{1,i}^{ 2}+Delta r_{2,i}^{2})end{bmatriz}}{begin{bmatriz}u_{1}\u_{2}\u_{3}end{bmatriz}} \&=-sum_{i=1}^{n}m_{i}[Delta r_{i}]^{2}mathbf {u} \[6pt]-sum_{i= 1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r}_{i}times mathbf {u})]&=left(-sum _{i=1}^{n}m_{i}[Delta r_{i}]^{2}right)mathbf {u} ;ldots ;mathbf {u} {text{ no es característico de }}P_{i}end{aligned}}}=-sum_{i=1}^{n}m_{i}[Delta r_{i}]^{2}mathbf {u} \[6pt]-sum_{i=1}^ {n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r}_{i}times mathbf { u})]&=left(-sum _{i=1}^{n}m_{i}[Delta r_{i}]^{2}right)mathbf {u} ;ldots ;mathbf {u} {text{ no es característico de }}P_{i}end{aligned}}}=-sum_{i=1}^{n}m_{i}[Delta r_{i}]^{2}mathbf {u} \[6pt]-sum_{i=1}^ {n}m_{i}[{boldsymbol {Delta }}mathbf {r} _{i}times ({boldsymbol {Delta }}mathbf {r}_{i}times mathbf { u})]&=left(-sum _{i=1}^{n}m_{i}[Delta r_{i}]^{2}right)mathbf {u} ;ldots ;mathbf {u} {text{ no es característico de }}P_{i}end{aligned}}}

Finalmente, el resultado se usa para completar la prueba principal de la siguiente manera:

{displaystyle {begin{alineado}{boldsymbol {tau }}&=-sum _{i=1}^{n}m_{i}[{boldsymbol {Delta }}mathbf {r} _ {i}times ({boldsymbol {Delta }}mathbf {r}_{i}times {boldsymbol {alpha }})]+{boldsymbol {omega }}times -sum _{i=1}^{n}m_{i}{boldsymbol {Delta}}mathbf {r}_{i}times ({boldsymbol {Delta}}mathbf {r}_{i }times {boldsymbol {omega }})]\&=left(-sum _{i=1}^{n}m_{i}[Delta r_{i}]^{2} derecha){boldsymbol {alpha }}+{boldsymbol {omega }}times left(-sum _{i=1}^{n}m_{i}[Delta r_{i}]^ {2}right){boldsymbol {omega }}end{alineado}}}

Por lo tanto, el momento de torsión resultante en el sistema rígido de partículas está dado por

{displaystyle {boldsymbol {tau }}=mathbf {I}_{mathbf {C} }{boldsymbol {alpha }}+{boldsymbol {omega }}times mathbf {I} _ {mathbf {C} }{boldsymbol {omega }},}

donde ${displaystyle mathbf {I_{C}} }$ es la matriz de inercia relativa al centro de masa.

Teorema del eje paralelo

La matriz de inercia de un cuerpo depende de la elección del punto de referencia. Existe una relación útil entre la matriz de inercia relativa al centro de masa $mathbf {C}$ y la matriz de inercia relativa a otro punto $mathbf{R}$ . Esta relación se llama teorema de los ejes paralelos.

Considere la matriz de inercia ${displaystyle mathbf {I_{R}} }$ obtenida para un sistema rígido de partículas medidas con respecto a un punto de referencia $mathbf{R}$ , dada por

{displaystyle mathbf {I}_{mathbf {R} }=-sum_{i=1}^{n}m_{i}left[mathbf {r}_{i}-mathbf { R} derecho]^{2}.}

Sea $mathbf {C}$ el centro de masa del sistema rígido, entonces

{displaystyle mathbf {R} =(mathbf {R} -mathbf {C})+mathbf {C} =mathbf {d} +mathbf {C},}

donde $mathbf{d}$ es el vector desde el centro de masa $mathbf {C}$ hasta el punto de referencia $mathbf{R}$ . Utilice esta ecuación para calcular la matriz de inercia,

{displaystyle mathbf {I}_{mathbf {R} }=-sum_{i=1}^{n}m_{i}[mathbf {r}_{i}-left(mathbf {C} +mathbf {d} right)]^{2}=-sum _{i=1}^{n}m_{i}[left(mathbf {r} _{i}- matemáticasbf {C} right)-mathbf {d} ]^{2}.}

Distribuir sobre el producto cruz para obtener

{displaystyle mathbf {I}_{mathbf {R} }=-left(sum_{i=1}^{n}m_{i}[mathbf {r}_{i}-mathbf {C} ]^{2}right)+left(sum _{i=1}^{n}m_{i}[mathbf {r} _{i}-mathbf {C} ]right)[mathbf {d} ]+[mathbf {d} ]left(sum_{i=1}^{n}m_{i}[mathbf {r}_{i}-mathbf {C } ]right)-left(sum _{i=1}^{n}m_{i}right)[mathbf {d} ]^{2}.}

El primer término es la matriz de inercia ${displaystyle mathbf {I_{C}} }$ relativa al centro de masa. Los términos segundo y tercero son cero por definición del centro de masa $mathbf {C}$ . Y el último término es la masa total del sistema multiplicada por el cuadrado de la matriz asimétrica ${ estilo de visualización [ mathbf {d}]}$ construida a partir de $mathbf{d}$ .

El resultado es el teorema del eje paralelo,

{displaystyle mathbf {I}_{mathbf {R} }=mathbf {I}_{mathbf {C} }-M[mathbf {d} ]^{2},}

donde $mathbf{d}$ es el vector desde el centro de masa $mathbf {C}$ hasta el punto de referencia $mathbf{R}$ .

Nota sobre el signo menos: al usar la matriz simétrica oblicua de los vectores de posición en relación con el punto de referencia, la matriz de inercia de cada partícula tiene la forma ${displaystyle -mleft[mathbf {r} right]^{2}}$ , que es similar a la $señor^{2}$ que aparece en el movimiento plano. Sin embargo, para que esto funcione correctamente, se necesita un signo menos. Este signo menos se puede absorber en el término ${displaystyle mleft[mathbf {r} right]^{mathsf {T}}left[mathbf {r} right]}$ , si se desea, utilizando la propiedad de simetría sesgada de ${ estilo de visualización [ mathbf {r}]}$ .

Momento de inercia escalar en un plano

El momento de inercia escalar, $ILLINOIS}$ , de un cuerpo con respecto a un eje específico cuya dirección está especificada por el vector unitario $mathbf{sombrero{k}}$ y pasa a través del cuerpo en un punto $mathbf{R}$ es el siguiente:

{displaystyle I_{L}=mathbf {hat {k}} cdot left(-sum _{i=1}^{N}m_{i}left[Delta mathbf {r}_ {i}right]^{2}right)mathbf {hat {k}} =mathbf {hat {k}} cdot mathbf {I}_{mathbf {R} }mathbf { sombrero {k}} =mathbf {sombrero {k}}^{mathsf{T}}mathbf{I}_{mathbf{R}}mathbf{sombrero{k}},}

donde ${displaystyle mathbf {I_{R}} }$ es el momento de la matriz de inercia del sistema relativo al punto de referencia $mathbf{R}$ , y ${ estilo de visualización [ Delta mathbf {r} _ {i}]}$ es la matriz simétrica oblicua obtenida del vector ${displaystyle Delta mathbf {r} _{i}=mathbf {r} _{i}-mathbf {R} }$ .

Esto se deriva de la siguiente manera. Sea un conjunto rígido de $norte$ partículas, ${displaystyle P_{i},i=1,puntos,n}$ , tenga coordenadas $mathbf {r} _{i}$ . Elija $mathbf{R}$ como punto de referencia y calcule el momento de inercia alrededor de una línea L definida por el vector unitario que pasa $mathbf{sombrero{k}}$ por el punto de referencia $mathbf{R}$ , ${displaystyle mathbf {L} (t)=mathbf {R} +tmathbf {hat {k}} }$ . El vector perpendicular de esta línea a la partícula $Pi}$ se obtiene ${ estilo de visualización Delta mathbf {r} _ {i}}$ quitando la componente que se proyecta sobre $mathbf{sombrero{k}}$ .

{displaystyleDeltamathbf{r}_{i}^{perp}=Deltamathbf{r}_{i}-left(mathbf{that{k}}cdotDeltamathbf {r} _{i}right)mathbf {hat {k}} =left(mathbf {E} -mathbf {hat {k}} mathbf {hat {k}} ^{ matemáticasf{T}}right)Deltamathbf{r}_{i},}

donde $mathbf {E}$ es la matriz identidad, para evitar confusiones con la matriz de inercia, y ${displaystyle mathbf {hat {k}} mathbf {hat {k}} ^{mathsf {T}}}$ es la matriz producto exterior formada a partir del vector unitario $mathbf{sombrero{k}}$ a lo largo de la recta $L$ .

Para relacionar este momento de inercia escalar con la matriz de inercia del cuerpo, introduzca la matriz simétrica oblicua ${displaystyle left[mathbf {hat {k}} right]}$ tal que ${displaystyleleft[mathbf{hat{k}}right]mathbf{y}=mathbf{hat{k}}timesmathbf{y}}$ , entonces tenemos la identidad

{displaystyle -left[mathbf {hat {k}} right]^{2}equiv left|mathbf {hat {k}}right|^{2}left(mathbf { E} -mathbf {hat {k}} mathbf {hat {k}} ^{mathsf {T}}right)=mathbf {E} -mathbf {hat {k}} mathbf {sombrero{k}}^{mathsf{T}},}

teniendo en cuenta que $mathbf{sombrero{k}}$ es un vector unitario.

La magnitud al cuadrado del vector perpendicular es

{displaystyle {begin{alineado}left|Delta mathbf {r} _{i}^{perp}right|^{2}&=left(-left[mathbf {hat { k}}right]^{2}Deltamathbf{r}_{i}right)cdotleft(-left[mathbf{hat{k}}right]^{2} Delta mathbf{r}_{i}right)\&=left(mathbf{hat{k}}timesleft(mathbf{hat{k}}timesDeltamathbf{ r} _{i}right)right)cdot left(mathbf{hat{k}}timesleft(mathbf{hat{k}}timesdeltamathbf{r}_ {i}derecha)derecha)end{alineado}}}

La simplificación de esta ecuación utiliza la identidad del triple producto escalar

{displaystyle left(mathbf {hat {k}} times left(mathbf {hat {k}} times Delta mathbf {r}_{i}right)right)cdot left(mathbf {hat {k}} times left(mathbf {hat {k}} times Delta mathbf {r} _{i}right)right)equiv left(left(mathbf {hat {k}} times left(mathbf {hat {k}} times Delta mathbf {r} _{i}right)right)times mathbf { hat {k}} right)cdot left(mathbf {hat {k}} times Delta mathbf {r} _{i}right),}

donde se han intercambiado los productos punto y cruz. Intercambiando productos y simplificando observando que ${ estilo de visualización Delta mathbf {r} _ {i}}$ y $mathbf{sombrero{k}}$ son ortogonales:

{displaystyle {begin{alineado}&left(mathbf {hat {k}} times left(mathbf {hat {k}} times Delta mathbf {r}_{i} derecha)derecha)cdot left(mathbf{hat{k}}timesleft(mathbf{hat{k}}timesDeltamathbf{r}_{i}right) derecha)\={}&left(left(mathbf{hat{k}}timesleft(mathbf{hat{k}}timesDeltamathbf{r}_{i} right)right)timesmathbf{hat{k}}right)cdotleft(mathbf{hat{k}}timesDeltamathbf{r}_{i}right) \={}&left(mathbf{hat{k}}timesDeltamathbf{r}_{i}right)cdot left(-Deltamathbf{r}_{i }timesmathbf{hat{k}}right)\={}&-mathbf{hat{k}}cdotleft(Deltamathbf{r}_{i}times Deltamathbf{r}_{i}timesmathbf{hat{k}}right)\={}&-mathbf{hat{k}}cdotleft[Deltamathbf{ r} _{i}right]^{2}mathbf {hat {k}}.end{alineado}}}

Por lo tanto, el momento de inercia alrededor de la línea que $L$ pasa $mathbf{R}$ en la dirección $mathbf{sombrero{k}}$ se obtiene del cálculo

{displaystyle {begin{aligned}I_{L}&=sum_{i=1}^{N}m_{i}left|Deltamathbf{r}_{i}^{perp} derecha|^{2}\&=-sum _{i=1}^{N}m_{i}mathbf {hat {k}} cdot left[Delta mathbf {r}_ { i}right]^{2}mathbf {hat {k}} =mathbf {hat {k}} cdot left(-sum _{i=1}^{N}m_{i } left[Deltamathbf{r}_{i}right]^{2}right)mathbf{hat{k}}\&=mathbf{hat{k}}cdot mathbf {I}_{mathbf{R}}mathbf{hat{k}} =mathbf{hat{k}} ^{mathsf{T}}mathbf{I} _{mathbf{R } }mathbf {sombrero {k}},end{alineado}}}

donde ${displaystyle mathbf {I_{R}} }$ es la matriz de momentos de inercia del sistema con respecto al punto de referencia $mathbf{R}$ .

Esto muestra que la matriz de inercia se puede utilizar para calcular el momento de inercia de un cuerpo alrededor de cualquier eje de rotación especificado en el cuerpo.

Tensor de inercia

Para el mismo objeto, diferentes ejes de rotación tendrán diferentes momentos de inercia sobre esos ejes. En general, los momentos de inercia no son iguales a menos que el objeto sea simétrico en todos los ejes. El momento de tensor de inercia es una forma conveniente de resumir todos los momentos de inercia de un objeto con una cantidad. Puede calcularse con respecto a cualquier punto del espacio, aunque a efectos prácticos se utiliza más comúnmente el centro de masa.

Definición

Para un objeto rígido de $norte$ masas puntuales $m_{k}$ , el tensor del momento de inercia viene dado por

{displaystyle mathbf {I} ={begin{bmatrix}I_{11}&I_{12}&I_{13}\I_{21}&I_{22}&I_{23}\I_{31}&I_{32 }&I_{33}end{bmatriz}}.}

Sus componentes se definen como

{displaystyle I_{ij} {stackrel {mathrm {def} }{=}} sum _{k=1}^{N}m_{k}left(left|mathbf {r } _{k}right|^{2}delta_{ij}-x_{i}^{(k)}x_{j}^{(k)}right)}

dónde

$i$ , $j$ es igual a 1, 2 o 3 para $X$ , $y$ y $z$ , respectivamente,
${displaystyle mathbf {r}_{k}=left(x_{1}^{(k)},x_{2}^{(k)},x_{3}^{(k)}right)}$ es el vector a la masa puntual $m_{k}$ desde el punto sobre el cual se calcula el tensor y
$delta _{ij}$ es el delta de Kronecker.

Tenga en cuenta que, por definición, $mathbf{yo}$ es un tensor simétrico.

Los elementos diagonales se escriben más sucintamente como

{displaystyle {begin{alineado}I_{xx} &{stackrel {mathrm {def} }{=}} sum_{k=1}^{N}m_{k}left(y_ {k}^{2}+z_{k}^{2}right),\I_{yy} &{stackrel {mathrm {def} }{=}} sum _{k=1 }^{N}m_{k}left(x_{k}^{2}+z_{k}^{2}right),\I_{zz} &{stackrel {mathrm {def} }{=}} sum _{k=1}^{N}m_{k}left(x_{k}^{2}+y_{k}^{2}right),end{alineado }}}

mientras que los elementos fuera de la diagonal, también llamados productos de inercia, son

{displaystyle {begin{alineado}I_{xy}=I_{yx} &{stackrel {mathrm {def} }{=}} -sum _{k=1}^{N}m_{ k}x_{k}y_{k},\I_{xz}=I_{zx} &{stackrel {mathrm {def} }{=}} -sum _{k=1}^{ N}m_{k}x_{k}z_{k},\I_{yz}=I_{zy} &{stackrel {mathrm {def} }{=}} -sum _{k= 1}^{N}m_{k}y_{k}z_{k}.end{alineado}}}

Aquí $yo_{{xx}}$ denota el momento de inercia alrededor del $X$ eje cuando los objetos giran alrededor del eje x, ${displaystyle I_{xy}}$ denota el momento de inercia alrededor del $y$ eje cuando los objetos giran alrededor del $X$ eje y así sucesivamente.

Estas cantidades se pueden generalizar a un objeto con masa distribuida, descrita por una función de densidad de masa, de manera similar al momento de inercia escalar. Uno entonces tiene

{displaystylemathbf{I} =iiint_{V}rho(x,y,z)left(|mathbf{r}|^{2}mathbf{E}_{3}- mathbf{r}otimesmathbf{r}right),dx,dy,dz,}

donde ${displaystyle mathbf {r} otimes mathbf {r} }$ es su producto exterior, E ₃ es la matriz identidad 3×3 y V es una región del espacio que contiene completamente el objeto.

Alternativamente, también se puede escribir en términos del operador de momento angular ${displaystyle [mathbf {r} ]mathbf {x} =mathbf {r} times mathbf {x} }$ :

{displaystyle mathbf{I} =iiint _{V}rho(mathbf{r})[mathbf{r}]^{textsf{T}}[mathbf{r}],dV= -iiint _{Q}rho(mathbf{r})[mathbf{r}]^{2},dV}

El tensor de inercia se puede usar de la misma manera que la matriz de inercia para calcular el momento escalar de inercia alrededor de un eje arbitrario en la dirección $matemáticas{n}$ ,

{displaystyle I_{n}=mathbf{n}cdotmathbf{I}cdotmathbf{n},}

donde se toma el producto escalar con los elementos correspondientes en los tensores componentes. Un término de producto de inercia tal como ${ estilo de visualización I_ {12}}$ se obtiene mediante el cálculo

{displaystyle I_{12}=mathbf{e}_{1}cdotmathbf{I}cdotmathbf{e}_{2},}

y puede interpretarse como el momento de inercia alrededor del $X$ eje cuando el objeto gira alrededor del $y$ eje.

Los componentes de los tensores de grado dos se pueden ensamblar en una matriz. Para el tensor de inercia esta matriz viene dada por,

{displaystyle mathbf {I} ={begin{bmatrix}I_{11}&I_{12}&I_{13}\I_{21}&I_{22}&I_{23}\I_{31}&I_{32 }&I_{33}end{bmatrix}}={begin{bmatrix}I_{xx}&I_{xy}&I_{xz}\I_{yx}&I_{yy}&I_{yz}\I_{zx} &I_{zy}&I_{zz}end{bmatriz}}={begin{bmatriz}sum _{k=1}^{N}m_{k}left(y_{k}^{2}+z_ {k}^{2}right)&-sum_{k=1}^{N}m_{k}x_{k}y_{k}&-sum_{k=1}^{N} m_{k}x_{k}z_{k}\-sum_{k=1}^{N}m_{k}x_{k}y_{k}&sum_{k=1}^{ N}m_{k}left(x_{k}^{2}+z_{k}^{2}right)&-sum_{k=1}^{N}m_{k}y_{k }z_{k}\-sum_{k=1}^{N}m_{k}x_{k}z_{k}&-sum_{k=1}^{N}m_{k} y_{k}z_{k}&sum _{k=1}^{N}m_{k}left(x_{k}^{2}+y_{k}^{2}right)end {bmatriz}}.}

Es común en la mecánica de cuerpos rígidos usar notación que identifique explícitamente los ejes $X$ , $y$ y $z$ -, como $yo_{{xx}}$ y ${displaystyle I_{xy}}$ , para los componentes del tensor de inercia.

Convención de inercia alternativa

Hay algunas aplicaciones CAD y CAE como SolidWorks, Unigraphics NX/Siemens NX y MSC Adams que utilizan una convención alternativa para los productos de inercia. De acuerdo con esta convención, el signo menos se elimina de las fórmulas del producto de inercia y en su lugar se inserta en la matriz de inercia:

Determinar la convención de inercia (método de los ejes principales)

Si se tiene el dato de inercia ${ estilo de visualización (I_{xx},I_{yy},I_{zz},I_{xy},I_{xz},I_{yz})}$ sin saber que convención de inercia se ha utilizado, se puede determinar si se tiene también los ejes principales. Con el método de los ejes principales, se elaboran matrices de inercia a partir de los dos supuestos siguientes:

Se ha utilizado la convención estándar de inercia ${ estilo de visualización (I_{12}=I_{xy},I_{13}=I_{xz},I_{23}=I_{yz})}$ .
Se ha utilizado la convención de inercia alternativa ${ estilo de visualización (I_{12}=-I_{xy},I_{13}=-I_{xz},I_{23}=-I_{yz})}$ .

A continuación, se calculan los vectores propios de las dos matrices. La matriz cuyos vectores propios son paralelos a los ejes principales corresponde a la convención de inercia que se ha utilizado.

Derivación de los componentes tensoriales

La distancia $r$ de una partícula at $mathbf{x}$ desde el eje de rotación que pasa por el origen en la $mathbf {sombrero {n}}$ dirección es ${displaystyleleft|mathbf{x} -left(mathbf{x}cdotmathbf{hat{n}}right)mathbf{hat{n}}right|}$ , donde $mathbf {sombrero {n}}$ es el vector unitario. El momento de inercia sobre el eje es

{displaystyle I=mr^{2}=mleft(mathbf {x} -left(mathbf {x} cdot mathbf {hat {n}} right)mathbf {hat {n }}right)cdot left(mathbf{x} -left(mathbf{x}cdotmathbf{hat{n}}right)mathbf{hat{n}}right) =mleft(mathbf{x}^{2}-2mathbf{x}left(mathbf{x}cdotmathbf{hat{n}}right)mathbf{hat{n }} +left(mathbf{x}cdotmathbf{hat{n}}right)^{2}mathbf{hat{n}} ^{2}right)=mleft(mathbf{x}^{2}-left(mathbf{x}cdotmathbf{hat{n}}right)^{2}right).}

Reescriba la ecuación usando la matriz transpuesta:

{displaystyle I=mleft(mathbf{x}^{textsf{T}}mathbf{x} -mathbf{hat{n}}^{textsf{T}}mathbf{x} mathbf{x}^{textsf{T}}mathbf{hat{n}}right)=mcdot mathbf{hat{n}}^{textsf{T}}left( mathbf{x}^{textsf{T}}mathbf{x}cdotmathbf{E_{3}} -mathbf{x}mathbf{x}^{textsf{T}}right) matemáticasbf{sombrero{n}},}

donde E ₃ es la matriz identidad 3×3.

Esto conduce a una fórmula tensorial para el momento de inercia

{displaystyle I=m{begin{bmatrix}n_{1}&n_{2}&n_{3}end{bmatrix}}{begin{bmatrix}y^{2}+z^{2}&-xy& -xz\-yx&x^{2}+z^{2}&-yz\-zx&-zy&x^{2}+y^{2}end{bmatriz}}{begin{bmatriz}n_{1 }\n_{2}\n_{3}end{matriz}}.}

Para partículas múltiples, solo necesitamos recordar que el momento de inercia es aditivo para ver que esta fórmula es correcta.

Tensor de inercia de traslación

Sea ${ estilo de visualización mathbf {I} _ {0}}$ el tensor de inercia de un cuerpo calculado en su centro de masa, y $mathbf{R}$ sea el vector desplazamiento del cuerpo. El tensor de inercia del cuerpo trasladado respecto a su centro de masa original viene dado por:

{displaystyle mathbf {I} =mathbf {I} _{0}+m[(mathbf {R} cdot mathbf {R})mathbf {E}_{3}-mathbf {R} otimes mathbf {R} ]}

donde $metro$ es la masa del cuerpo, E ₃ es la matriz identidad 3 × 3 y $otimes$ es el producto exterior.

Tensor de inercia de rotación

Sea $mathbf{R}$ la matriz que representa la rotación de un cuerpo. El tensor de inercia del cuerpo girado viene dado por:

{displaystyle mathbf {I} =mathbf {R} mathbf {I_{0}} mathbf {R} ^{textsf {T}}}

Matriz de inercia en diferentes marcos de referencia

El uso de la matriz de inercia en la segunda ley de Newton supone que sus componentes se calculan en relación con ejes paralelos al marco de inercia y no en relación con un marco de referencia fijo en el cuerpo. Esto significa que a medida que el cuerpo se mueve, los componentes de la matriz de inercia cambian con el tiempo. Por el contrario, las componentes de la matriz de inercia medidas en un marco fijo al cuerpo son constantes.

Marco del cuerpo

Denotemos la matriz de inercia del marco del cuerpo con respecto al centro de masa ${displaystyle mathbf {I}_{mathbf {C} }^{B}}$ , y defina la orientación del marco del cuerpo con respecto al marco de inercia por la matriz de rotación $matemáticas {A}$ , tal que,

{displaystyle mathbf {x} =mathbf {A} mathbf {y},}

donde los vectores $mathbf {y}$ en el marco de coordenadas fijo del cuerpo tienen coordenadas $mathbf{x}$ en el marco inercial. Entonces, la matriz de inercia del cuerpo medida en el marco inercial está dada por

{displaystyle mathbf {I}_{mathbf {C} }=mathbf {A} mathbf {I}_{mathbf {C} }^{B}mathbf {A} ^{mathsf {T }}.}

Observe que $matemáticas {A}$ cambia a medida que el cuerpo se mueve, mientras ${displaystyle mathbf {I}_{mathbf {C} }^{B}}$ permanece constante.

Ejes principales

Medida en el marco del cuerpo, la matriz de inercia es una matriz simétrica real constante. Una matriz simétrica real tiene la descomposición propia en el producto de una matriz de rotación $mathbf {Q}$ y una matriz diagonal ${displaystyle {boldsymbol {Lambda}}}$ , dada por

{displaystyle mathbf {I}_{mathbf {C} }^{B}=mathbf {Q} {boldsymbol {Lambda }}mathbf {Q} ^{mathsf {T}},}

dónde

{displaystyle {boldsymbol {Lambda }}={begin{bmatrix}I_{1}&0&0\0&I_{2}&0\0&0&I_{3}end{bmatrix}}.}

Las columnas de la matriz de rotación $mathbf {Q}$ definen las direcciones de los ejes principales del cuerpo y las constantes $yo_{1}$ , $yo_{2}$ y $yo_{3}$ se denominan momentos principales de inercia. Este resultado fue mostrado por primera vez por JJ Sylvester (1852), y es una forma de la ley de inercia de Sylvester. El eje principal con el mayor momento de inercia a veces se denomina eje de figura o eje de figura.

Un trompo de juguete es un ejemplo de un cuerpo rígido giratorio, y la palabra trompo se usa en los nombres de los tipos de cuerpos rígidos. Cuando todos los momentos principales de inercia son distintos, los ejes principales que pasan por el centro de masa se especifican de forma única y el cuerpo rígido se denomina peonza asimétrica. Si dos momentos principales son iguales, el cuerpo rígido se denomina trompo simétrico y no hay elección única para los dos ejes principales correspondientes. Si los tres momentos principales son iguales, el cuerpo rígido se denomina trompo esférico (aunque no es necesario que sea esférico) y cualquier eje puede considerarse un eje principal, lo que significa que el momento de inercia es el mismo con respecto a cualquier eje.

Los ejes principales suelen estar alineados con los ejes de simetría del objeto. Si un cuerpo rígido tiene un eje de simetría de orden $metro$ , lo que significa que es simétrico bajo rotaciones de 360°/ m alrededor del eje dado, ese eje es un eje principal. Cuando $metro > 2$ , el cuerpo rígido es un trompo simétrico. Si un cuerpo rígido tiene al menos dos ejes de simetría que no son paralelos ni perpendiculares entre sí, es un trompo esférico, por ejemplo, un cubo o cualquier otro sólido platónico.

El movimiento de los vehículos a menudo se describe en términos de guiñada, cabeceo y balanceo, que generalmente corresponden aproximadamente a rotaciones alrededor de los tres ejes principales. Si el vehículo tiene simetría bilateral entonces uno de los ejes principales corresponderá exactamente al eje transversal (cabeceo).

Un ejemplo práctico de este fenómeno matemático es la tarea automotriz rutinaria de balancear una llanta, que básicamente significa ajustar la distribución de masa de una rueda de automóvil de manera que su eje principal de inercia esté alineado con el eje para que la rueda no se tambalee.

Las moléculas giratorias también se clasifican como tapas asimétricas, simétricas o esféricas, y la estructura de sus espectros de rotación es diferente para cada tipo.

Elipsoide

El momento de la matriz de inercia en coordenadas cuerpo-marco es una forma cuadrática que define una superficie en el cuerpo llamada elipsoide de Poinsot. Sea ${displaystyle {boldsymbol {Lambda}}}$ la matriz de inercia relativa al centro de masas alineada con los ejes principales, luego la superficie

{displaystyle mathbf {x} ^{mathsf {T}}{boldsymbol {Lambda }}mathbf {x} =1,}

{displaystyle I_{1}x^{2}+I_{2}y^{2}+I_{3}z^{2}=1,}

define un elipsoide en el marco del cuerpo. Escribe esta ecuación en la forma,

{displaystyle left({frac {x}{1/{sqrt {I_{1}}}}}right)^{2}+left({frac {y}{1/{sqrt {I_{2}}}}}derecha)^{2}+izquierda({frac {z}{1/{sqrt {I_{3}}}}}derecha)^{2}=1,}

para ver que los diámetros semiprincipales de este elipsoide están dados por

{displaystyle a={frac {1}{sqrt {I_{1}}}},quad b={frac {1}{sqrt {I_{2}}}},quad c={ frac {1}{sqrt {I_{3}}}}.}

Defina un punto $mathbf{x}$ en este elipsoide en términos de su magnitud y dirección ${displaystyle mathbf {x} =|mathbf {x} |mathbf {n} }$ , donde $matemáticas{n}$ es un vector unitario. Entonces, la relación presentada anteriormente, entre la matriz de inercia y el momento de inercia escalar ${displaystyle I_{mathbf{n} }}$ alrededor de un eje en la dirección $matemáticas{n}$ , produce

{displaystylemathbf{x}^{mathsf{T}}{ballsymbol {lambda}}mathbf{x} =|mathbf{x}|^{2}mathbf{n}^{ mathsf{T}}{ballsymbol {Lambda}}mathbf{n} =|mathbf{x}|^{2}I_{mathbf{n}}=1.}

Por lo tanto, la magnitud de un punto $mathbf{x}$ en la dirección $matemáticas{n}$ del elipsoide de inercia es

{displaystyle |mathbf {x} |={frac {1}{sqrt {I_{mathbf {n} }}}}.}

Contenido relacionado

Más resultados...