Moiré patrón

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Patrón de interferencia

Un patrón de moiré, formado por dos conjuntos de líneas paralelas, uno inclinado a un ángulo de 5° al otro

Las líneas finas que componen el cielo en esta imagen crean patrones moiré cuando se muestran en algunas resoluciones por la misma razón que las fotografías de televisión exhiben patrones moiré: las líneas no son absolutamente de nivel.

Diferencia en la distancia de la valla delantera y trasera en un puente crear patrones moiré.

Moiré patrón apareciendo en capturas de cámara escalada de pantalla LCD

En matemáticas, física y arte, moiré patterns (MWAR-ay, mwar-AY, Francés:[mwaʁe] ()escucha)) o moiré fringes son patrones de interferencia a gran escala que se pueden producir cuando un patrón opaque gobernado con brechas transparentes se superpone en otro patrón similar. Para que el patrón de interferencia moiré aparezca, los dos patrones no deben ser completamente idénticos, sino desplazados, rotados, o tener un lanzamiento ligeramente diferente.

Los patrones muaré aparecen en muchas situaciones. En la impresión, el patrón de puntos impreso puede interferir con la imagen. En televisión y fotografía digital, un patrón en un objeto fotografiado puede interferir con la forma de los sensores de luz para generar artefactos no deseados. A veces también se crean deliberadamente: en micrómetros se utilizan para amplificar los efectos de movimientos muy pequeños.

En física, su manifestación es la interferencia de ondas, como la que se observa en el experimento de la doble rendija y el fenómeno del latido en acústica.

Etimología

El término proviene de moire (moiré en su adjetivo francés), un tipo de textil, tradicionalmente hecho de seda pero ahora también de algodón o fibra sintética, con un ondulado o "regado" apariencia. El muaré, o "tejido regado", se fabrica presionando dos capas del tejido cuando está húmedo. El espaciado similar pero imperfecto de los hilos crea un patrón característico que permanece después de que se seca la tela.

En francés, el sustantivo moire está en uso desde el siglo XVII, para "seda regada". Fue un préstamo del mohair inglés (certificado en 1610). En el uso francés, el sustantivo dio origen al verbo moirer, "producir un textil regado tejiendo o presionando", en el siglo XVIII. El adjetivo moiré formado a partir de este verbo está en uso desde al menos 1823.

Formación de patrones

Línea moiré con movimiento lento de la capa reveladora hacia arriba

Shape moiré

Moiré patrón creado por superposición de dos conjuntos de círculos concéntricos

Los patrones de muaré suelen ser un artefacto de las imágenes producidas por diversas técnicas de imágenes digitales y gráficos por computadora, por ejemplo, al escanear una imagen de medios tonos o trazar rayos en un plano cuadriculado (este último es un caso especial de aliasing, debido al submuestreo de una imagen regular fina). patrón). Esto se puede superar en el mapeo de texturas mediante el uso de mipmapping y filtrado anisotrópico.

El dibujo de la parte superior derecha muestra un patrón muaré. Las líneas podrían representar fibras en seda muaré, o líneas dibujadas en papel o en una pantalla de computadora. La interacción no lineal de los patrones ópticos de las líneas crea un patrón real y visible de bandas claras y oscuras aproximadamente paralelas, el patrón muaré, superpuesto a las líneas.

El efecto muaré también se produce entre objetos transparentes superpuestos. Por ejemplo, una máscara de fase invisible está hecha de un polímero transparente con un perfil de espesor ondulado. A medida que la luz brilla a través de dos máscaras superpuestas de patrones de fase similares, aparece un amplio patrón muaré en una pantalla a cierta distancia. Este efecto muaré de fase y el efecto muaré clásico de líneas opacas son dos extremos de un espectro continuo en óptica, que se denomina efecto muaré universal. El efecto muaré de fase es la base de un tipo de interferómetro de banda ancha en aplicaciones de ondas de partículas y rayos X. También proporciona una forma de revelar patrones ocultos en capas invisibles.

Línea muaré

Line muaré es un tipo de patrón muaré; un patrón que aparece cuando se superponen dos capas transparentes que contienen patrones opacos correlacionados. Line moiré es el caso cuando los patrones superpuestos comprenden líneas rectas o curvas. Al mover los patrones de capa, los patrones de muaré se transforman o se mueven a mayor velocidad. Este efecto se denomina aceleración de muaré óptico.

Se crean patrones muaré de líneas más complejos si las líneas son curvas o no exactamente paralelas.

Forma muaré

Moiré de forma es un tipo de patrón de moiré que demuestra el fenómeno de la ampliación del moiré. El moiré de forma 1D es el caso simplificado particular del moiré de forma 2D. Pueden aparecer patrones unidimensionales al superponer una capa opaca que contiene pequeñas líneas horizontales transparentes sobre una capa que contiene una forma compleja que se repite periódicamente a lo largo del eje vertical.

Los patrones muaré que revelan formas complejas o secuencias de símbolos incrustados en una de las capas (en forma de formas comprimidas que se repiten periódicamente) se crean con moiré de forma, también llamados patrones muaré de banda. Una de las propiedades más importantes del moiré de forma es su capacidad para ampliar formas diminutas a lo largo de uno o ambos ejes, es decir, estirarse. Un ejemplo 2D común de aumento de muaré ocurre cuando se ve una cerca de tela metálica a través de una segunda cerca de tela metálica de diseño idéntico. La fina estructura del diseño es visible incluso a grandes distancias.

Cálculos

Muaré de patrones paralelos

Enfoque geométrico

Los patrones están superpuestos en el ancho medio de la figura.

Moiré obtenido por la superimposición de dos patrones similares rotados por un ángulo

α

Considere dos patrones hechos de líneas paralelas y equidistantes, por ejemplo, líneas verticales. El paso del primer patrón es $p$ , el paso del segundo es $p + δp$ , con $0 < δp < p$ .

Si las líneas de los patrones se superponen a la izquierda de la figura, el desplazamiento entre las líneas aumenta al ir hacia la derecha. Después de un número dado de líneas, los patrones se oponen: las líneas del segundo patrón están entre las líneas del primer patrón. Si miramos de lejos, tenemos la sensación de zonas pálidas cuando las líneas están superpuestas (hay blanco entre líneas), y de zonas oscuras cuando las líneas están "opuestas".

La mitad de la primera zona oscura es cuando el cambio es igual a $p / 2$ . La $n$ ésima línea del segundo patrón se desplaza $n δp$ en comparación con la $n$ ésima línea de la primera red. El centro de la primera zona oscura corresponde así a

{displaystyle ncdot delta p={frac {p}{2}}}

{displaystyle n={frac {p}{2delta p}}.}

d

{displaystyle d=ncdot (p+delta p)={frac {p^{2}}{2delta p}}+{frac {p}{2}}}

{displaystyle 2d={frac {p^{2}}{delta p}}+p}

Cuanto mayor sea el paso, mayor será la distancia entre las zonas pálidas y oscuras;
más grande la discrepancia $δp$ , cuanto más cerca las zonas oscuras y pálidas; un gran espaciado entre las zonas oscuras y pálidas significa que los patrones tienen pasos muy cercanos.

El principio del moiré es similar a la escala Vernier.

Enfoque de funciones matemáticas

Moiré patrón (bottom) creado por superponer dos rejillas (top y medio)

La esencia del efecto muaré es la percepción (principalmente visual) de un tercer patrón claramente diferente causado por la superposición inexacta de dos patrones similares. La representación matemática de estos patrones no se obtiene de manera trivial y puede parecer algo arbitraria. En esta sección daremos un ejemplo matemático de dos patrones paralelos cuya superposición forma un patrón muaré, y mostraremos una forma (de muchas formas posibles) de que estos patrones y el efecto muaré se puedan representar matemáticamente.

La visibilidad de estos patrones depende del medio o sustrato en el que aparecen, y pueden ser opacos (como, por ejemplo, en papel) o transparentes (como, por ejemplo, en una película de plástico). A los efectos de la discusión, supondremos que los dos patrones primarios están impresos en tinta en escala de grises en una hoja blanca, donde la opacidad (p. ej., sombra de gris) del "impreso" parte viene dada por un valor entre 0 (blanco) y 1 (negro) inclusive, con 1/2 que representa el gris neutro. Cualquier valor menor que 0 o mayor que 1 usando esta escala de grises es esencialmente "no imprimible".

También elegiremos representar la opacidad del patrón que resulta de imprimir un patrón encima del otro en un punto dado del papel como el promedio (es decir, la media aritmética) de la opacidad de cada patrón en esa posición, que es la mitad de su suma, y, como se calcula, no excede 1. (Esta elección no es única. Cualquier otro método para combinar las funciones que satisfaga manteniendo el valor de la función resultante dentro de los límites [0,1] también servirá; aritmética promediar tiene la virtud de la simplicidad, con un daño mínimo a los conceptos del proceso de grabado).

Ahora consideramos la "impresión" superposición de dos patrones en escala de grises casi similares, que varían sinusoidalmente, para mostrar cómo producen un efecto muaré al imprimir primero un patrón en el papel y luego imprimir el otro patrón sobre el primero, manteniendo sus ejes de coordenadas en el registro. Representamos la intensidad de gris en cada patrón mediante una función de distancia de opacidad positiva a lo largo de una dirección fija (digamos, la coordenada x) en el plano de papel, en la forma

{displaystyle f={frac {1+sin(kx)}{2}}}

donde la presencia de 1 mantiene la función definida positiva, y la división por 2 evita valores de función mayores que 1.

La cantidad $k$ representa la variación periódica (es decir, la frecuencia espacial) de la intensidad de gris del patrón, medida como el número de ciclos de intensidad por unidad de distancia. Dado que la función seno es cíclica sobre los cambios de argumento de $2π$ , el incremento de distancia $Δ x$ por intensidad ciclo (la longitud de onda) se obtiene cuando $k Δ x = 2π$ , o $Δ x = 2π / k$ .

Considere ahora dos de estos patrones, donde uno tiene una variación periódica ligeramente diferente del otro:

{displaystyle {begin{aligned}f_{1}&={frac {1+sin(k_{1}x)}{2}}\[4pt]f_{2}&={frac {1+sin(k_{2}x)}{2}}end{aligned}}}

tal que $k 1 \approx k 2$ .

El promedio de estas dos funciones, que representan la imagen impresa superpuesta, se evalúa de la siguiente manera (ver identidades inversas aquí: prostaféresis):

{displaystyle {begin{aligned}f_{3}&={frac {f_{1}+f_{2}}{2}}\[5pt]&={frac {1}{2}}+{frac {sin(k_{1}x)+sin(k_{2}x)}{4}}\[5pt]&={frac {1+sin(Ax)cos(Bx)}{2}}end{aligned}}}

donde se demuestra fácilmente que

{displaystyle A={frac {k_{1}+k_{2}}{2}}}

{displaystyle B={frac {k_{1}-k_{2}}{2}}.}

Esta función promedio, $f 3$ , claramente se encuentra en el rango [0,1]. Dado que la variación periódica $A$ es el promedio y, por lo tanto, cercano a $k 1$ y $k 2$ , el efecto muaré se demuestra claramente por la envolvente sinusoidal "beat" función $cos(Bx)$ , cuya variación periódica es la mitad de la diferencia de las variaciones periódicas $k 1$ y $k 2$ (y evidentemente mucho más bajos en frecuencia).

Otros efectos muaré unidimensionales incluyen el clásico tono de frecuencia de pulsación que se escucha cuando dos notas puras de tono casi idéntico suenan simultáneamente. Esta es una versión acústica del efecto muaré en una dimensión del tiempo: las dos notas originales todavía están presentes, pero la percepción del oyente es de dos tonos que son el promedio de y medio la diferencia de las frecuencias de las dos notas. El aliasing en el muestreo de señales variables en el tiempo también pertenece a este paradigma moiré.

Patrones rotados

Considere dos patrones con el mismo paso $p$ , pero el segundo patrón gira un ángulo $α$ . Visto de lejos, también podemos ver líneas más oscuras y más claras: las líneas pálidas corresponden a las líneas de los nodos, es decir, líneas que pasan por las intersecciones de los dos patrones.

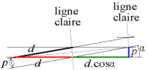
Si consideramos una celda de la red formada, podemos ver que es un rombo con los cuatro lados iguales a $d = p / sin α$ ; (tenemos un triángulo rectángulo cuya hipotenusa es $d$ y el lado opuesto al ángulo $α$ es $p$ ).

Unidad de la "net"; "ligne claire" significa "línea de pago".

Efecto del ángulo cambiante

Las líneas pálidas corresponden a la pequeña diagonal del rombo. Como las diagonales son las bisectrices de los lados vecinos, podemos ver que la línea pálida forma un ángulo igual a $α / 2$ con la perpendicular de la línea de cada patrón.

Además, el espacio entre dos líneas pálidas es $D$ , la mitad de la diagonal larga. La diagonal larga $2 D$ es la hipotenusa de un triángulo rectángulo y los lados del ángulo recto son $d (1 + cos α)$ y $p$ . El teorema de Pitágoras da:

{displaystyle (2D)^{2}=d^{2}(1+cos alpha)^{2}+p^{2}}

{displaystyle {begin{aligned}(2D)^{2}&={frac {p^{2}}{sin ^{2}alpha }}(1+cos alpha)^{2}+p^{2}\[5pt]&=p^{2}cdot left({frac {(1+cos alpha)^{2}}{sin ^{2}alpha }}+1right)end{aligned}}}

{displaystyle {begin{aligned}(2D)^{2}&=2p^{2}cdot {frac {1+cos alpha }{sin ^{2}alpha }}\[5pt]D&={frac {frac {p}{2}}{sin {frac {alpha }{2}}}}.end{aligned}}}

Efecto en líneas curvas

Cuando $α$ es muy pequeño ( $α < π / 6$ ) se pueden hacer las siguientes aproximaciones de ángulo pequeño:

{displaystyle {begin{aligned}sin alpha &approx alpha \cos alpha &approx 1end{aligned}}}

{displaystyle Dapprox {frac {p}{alpha }}.}

Podemos ver que cuanto menor es $α$ , más separadas están las líneas pálidas; cuando ambos patrones son paralelos ( $α = 0$ ), el espacio entre las líneas pálidas es infinito (no hay línea pálida).

Por lo tanto, hay dos formas de determinar $α$ : por la orientación de las líneas pálidas y por su espaciado

{displaystyle alpha approx {frac {p}{D}}}

Implicaciones y aplicaciones

Impresión de imágenes a todo color

Advertencia: peligro de incautación epiléptica audiogénico. El producto de dos "gran pistas" de velocidades ligeramente diferentes superpuestas, produciendo un patrón de moiré audible; si los latidos de una pista corresponden a donde en el espacio existe un punto o línea negro y los latidos de la otra pista corresponden a los puntos en el espacio donde una cámara es la luz de muestreo, porque las frecuencias no son exactamente iguales y alineadas perfectamente juntos, los latidos (o muestras) se alinearán estrechamente en algunos momentos lejanos. Los latidos más cercanos son, más oscuro está en ese lugar; más lejos, más ligero. El resultado es periódico de la misma manera que un patrón gráfico moiré. Ver: fingiendo.

En artes gráficas y preimpresión, la tecnología habitual para la impresión de imágenes a todo color implica la superposición de pantallas de medios tonos. Estos son patrones de puntos rectangulares regulares, a menudo cuatro de ellos, impresos en cian, amarillo, magenta y negro. Algún tipo de patrón muaré es inevitable, pero en circunstancias favorables el patrón es "ajustado"; es decir, la frecuencia espacial del muaré es tan alta que no se nota. En las artes gráficas, el término moiré significa un patrón de moiré excesivamente visible. Parte del arte de la preimpresión consiste en seleccionar ángulos de pantalla y frecuencias de medios tonos que minimicen el moiré. La visibilidad del muaré no es del todo predecible. El mismo conjunto de pantallas puede producir buenos resultados con algunas imágenes, pero muaré visible con otras.

Pantallas de televisión y fotografías

Fuerte moiré visible en esta foto de las plumas de un loro (más pronunciada en la imagen de tamaño completo)

Patrón Moiré visto sobre una jaula en el zoológico de San Francisco

Los patrones muaré se ven comúnmente en las pantallas de televisión cuando una persona usa una camisa o una chaqueta de un tejido o patrón en particular, como una chaqueta de pata de gallo. Esto se debe al escaneo entrelazado en televisores y cámaras que no son de película, lo que se conoce como twitter interlineado. A medida que la persona se mueve, el patrón muaré es bastante perceptible. Por ello, se instruye a los presentadores de noticias y otros profesionales que aparecen regularmente en la televisión para que eviten la ropa que podría causar el efecto.

Las fotografías de una pantalla de televisión tomadas con una cámara digital a menudo muestran patrones muaré. Dado que tanto la pantalla del televisor como la cámara digital utilizan una técnica de exploración para producir o capturar imágenes con líneas de exploración horizontales, los conjuntos de líneas en conflicto provocan los patrones muaré. Para evitar el efecto, la cámara digital puede apuntar a un ángulo de 30 grados con respecto a la pantalla del televisor.

Navegación marítima

El efecto muaré se utiliza en las balizas costeras denominadas "Marcas principales de Inogon" o "Luces Inogon", fabricadas por Inogon Licens AB, Suecia, para designar la ruta de viaje más segura para los barcos que se dirigen a esclusas, puertos deportivos, puertos, etc., o para indicar peligros bajo el agua (como tuberías o cables). El efecto muaré crea flechas que apuntan hacia una línea imaginaria que marca el peligro o la línea de paso seguro; a medida que los navegantes pasan sobre la línea, las flechas de la baliza parecen convertirse en bandas verticales antes de cambiar nuevamente a flechas que apuntan en la dirección opuesta. Se puede encontrar un ejemplo en el Reino Unido en la costa este de Southampton Water, frente a la refinería de petróleo Fawley (50°51′21.63″N 1°19′44.77″W / 50.8560083°N 1.3291028°O / 50.8560083; -1.3291028). Se pueden usar balizas de efecto muaré similares para guiar a los navegantes al punto central de un puente que se aproxima; cuando el buque está alineado con la línea central, las líneas verticales son visibles. Las luces Inogon se despliegan en los aeropuertos para ayudar a los pilotos en tierra a mantenerse en la línea central mientras atracan en el soporte.

Medición de deformaciones

Uso del efecto moiré en la medición de la cepa: caso de tracción uniaxial (top) y de tijera pura (bottom); las líneas de los patrones son inicialmente horizontales en ambos casos

En las industrias manufactureras, estos patrones se utilizan para estudiar la deformación microscópica de los materiales: al deformar una cuadrícula con respecto a una cuadrícula de referencia y medir el patrón muaré, se pueden deducir los niveles y patrones de tensión. Esta técnica es atractiva porque la escala del patrón muaré es mucho mayor que la desviación que lo provoca, lo que facilita la medición.

El efecto muaré se puede utilizar en la medición de deformación: el operador solo tiene que dibujar un patrón en el objeto y superponer el patrón de referencia al patrón deformado en el objeto deformado.

Se puede obtener un efecto similar mediante la superposición de una imagen holográfica del objeto al objeto mismo: el holograma es el paso de referencia, y la diferencia con el objeto son las deformaciones, que aparecen como líneas pálidas y oscuras.

Procesamiento de imágenes

Algunos programas informáticos de escaneo de imágenes proporcionan un filtro opcional, llamado "descreen" filtro, para eliminar los artefactos del patrón Moiré que, de lo contrario, se producirían al escanear imágenes impresas en medios tonos para producir imágenes digitales.

Billetes

Muchos billetes aprovechan la tendencia de los escáneres digitales a producir patrones muaré al incluir diseños finos circulares u ondulados que probablemente muestren un patrón muaré cuando se escanean e imprimen.

Microscopía

En la microscopía de superresolución, el patrón muaré se puede utilizar para obtener imágenes con una resolución superior al límite de difracción, utilizando una técnica conocida como microscopía de iluminación estructurada.

En la microscopía de túnel de barrido, aparecen franjas de muaré si las capas atómicas superficiales tienen una estructura cristalina diferente a la del cristal a granel. Esto puede deberse, por ejemplo, a la reconstrucción de la superficie del cristal, o cuando una capa delgada de un segundo cristal está en la superficie, p. grafeno monocapa, bicapa o heteroestructura de Van der Waals de grafeno y hBN, o nanoestructuras de bismuto y antimonio.

En la microscopía electrónica de transmisión (TEM), las franjas de muaré de traslación se pueden ver como líneas de contraste paralelas formadas en imágenes TEM de contraste de fase por la interferencia de planos de red cristalina difractante que se superponen y que pueden tener un espaciado u orientación diferente. La mayoría de las observaciones de contraste de muaré reportadas en la literatura se obtienen utilizando imágenes de contraste de fase de alta resolución en TEM. Sin embargo, si se utilizan imágenes de microscopía electrónica de transmisión de barrido de campo oscuro anular de alto ángulo con corrección de aberración de sonda (HAADF-STEM), se obtiene una interpretación más directa de la estructura cristalina en términos de tipos de átomos y posiciones.

Ciencia de los materiales y física de la materia condensada

Cuando el grafeno se cultiva en la superficie (111) del iridium, su modulación de altura de longitud de onda larga se puede considerar como un patrón moiré derivado de la superposición de las dos lattices hexagonales desajustadas.

Moiré patrón derivado de la superposición de dos lattices de grafeno torcido por 4°.

En la física de la materia condensada, el fenómeno muaré se analiza comúnmente para materiales bidimensionales. El efecto se produce cuando hay una discrepancia entre el parámetro de red o el ángulo de la capa 2D y el del sustrato subyacente u otra capa 2D, como en las heteroestructuras de materiales 2D. El fenómeno se explota como un medio de ingeniería de la estructura electrónica o las propiedades ópticas de los materiales, que algunos llaman materiales muaré. Los cambios a menudo significativos en las propiedades electrónicas al torcer dos capas atómicas y la perspectiva de aplicaciones electrónicas han llevado al nombre de twistrónica a este campo. Un ejemplo destacado es el grafeno bicapa retorcido, que forma un patrón muaré y en un ángulo mágico particular exhibe superconductividad y otras propiedades electrónicas importantes.

En la ciencia de los materiales, los ejemplos conocidos que exhiben contraste moiré son películas delgadas o nanopartículas de tipo MX (M = Ti, Nb; X = C, N) que se superponen con una matriz austenítica. Ambas fases, MX y la matriz, tienen una estructura cristalina cúbica centrada en las caras y una relación de orientación de cubo sobre cubo. Sin embargo, tienen un desajuste de red significativo de alrededor del 20 al 24 % (según la composición química de la aleación), lo que produce un efecto muaré.

Contenido relacionado

Más resultados...