Módulo inyectivo

En matemáticas, especialmente en el área del álgebra abstracta conocida como teoría de módulos, un módulo inyectivo es un módulo Q que comparte ciertas propiedades deseables con el Z. -módulo Q de todos los números racionales. Específicamente, si Q es un submódulo de algún otro módulo, entonces ya es un sumando directo de ese módulo; Además, dado un submódulo de un módulo Y, cualquier homomorfismo de módulo de este submódulo a Q se puede extender a un homomorfismo de todo Y a Q. Este concepto es dual al de módulos proyectivos. Los módulos inyectivos se introdujeron en (Baer 1940) y se analizan con cierto detalle en el libro de texto (Lam 1999, §3).

Los módulos inyectivos han sido ampliamente estudiados y se definen una variedad de nociones adicionales en términos de ellos: Los cogeneradores inyectivos son módulos inyectivos que representan fielmente toda la categoría de módulos. Las resoluciones inyectivas miden qué tan lejos está un módulo de inyectivo en términos de la dimensión inyectiva y representan módulos en la categoría derivada. Los cascos inyectivos son extensiones esenciales máximas y resultan ser extensiones inyectivas mínimas. En un anillo noetheriano, cada módulo inyectivo es únicamente una suma directa de módulos indescomponibles y su estructura se comprende bien. Un módulo inyectivo sobre un anillo puede no serlo sobre otro, pero existen métodos bien comprendidos para cambiar anillos que manejan casos especiales. Los anillos que son en sí mismos módulos inyectivos tienen una serie de propiedades interesantes e incluyen anillos como anillos de grupos de grupos finitos sobre campos. Los módulos inyectivos incluyen grupos divisibles y están generalizados por la noción de objetos inyectivos en la teoría de categorías.

Definición

Un módulo izquierdo Q sobre el anillo R es inyectivo si satisface una (y por lo tanto todas) de las siguientes condiciones equivalentes:

• Si Q es un submodulo de alguna otra izquierda R- Mobiliario M, entonces existe otro submodulo K de M tales que M es la suma directa interna Q y K, es decir. Q + K = M y Q ∩ K = {0}.
• Cualquier breve secuencia exacta 0 →Q → M → K → 0 de la izquierda R-Modules se separan.
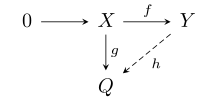
• Si X y Y quedan R-módulos, f: X → Y es un módulo inyectable homomorfismo y g: X → Q es un módulo arbitrario homomorfismo, entonces existe un módulo homomorfismo h: Y → Q tales que h = g, es decir, que el siguiente diagrama conmuta:

• The contravariant Hom functor Hom(-,Q) de la categoría de izquierda R-módulos a la categoría de grupos abelianos es exacto.

Los módulos R derechos inyectivos se definen en completa analogía.

Ejemplos

Primeros ejemplos

Trivialmente, el módulo cero {0} es inyectivo.

Dado un campo k, cada espacio vectorial k Q es un módulo k inyectivo. Motivo: si Q es un subespacio de V, podemos encontrar una base de Q y extenderla a una base de V. Los nuevos vectores de base extensible abarcan un subespacio K de V y V es la suma directa interna de Q y < i>K. Tenga en cuenta que el complemento directo K de Q no está determinado únicamente por Q, y de la misma manera el mapa extensible h en La definición anterior normalmente no es única.

Los racionales Q (con adición) forman un grupo abeliano inyectivo (es decir, un módulo Z inyectivo). El grupo de factores Q/Z y el grupo circular también son módulos Z inyectivos. El grupo de factores Z/nZ para n > 1 es inyectivo como módulo Z/nZ, pero no inyectivo como grupo abeliano.

Ejemplos conmutativos

Más generalmente, para cualquier dominio integral R con campo de fracciones K, el R- Mobiliario K es un inyector R-modulo, y de hecho el inyector más pequeño R- módulo que contiene R. Para cualquier dominio Dedekind, el módulo de referencia K/R es también inyector, y sus sumideros indecompuestos son las localizaciones ${displaystyle R_{mathfrak {p}/R}$ para los ideales no cero ${displaystyle {Mathfrak}}$. El cero ideal también es primo y corresponde al inyector K. De esta manera hay una correspondencia 1-1 entre ideales primos y módulos inyectores indecompuestos.

Una teoría particularmente rica está disponible para anillos noetherianos conmutativos debido a Eben Matlis (Lam 1999, §3I). Cada módulo inyectable es una suma directa de módulos inyectables indecompuestos, y los módulos inyectables indecompuestos se identifican únicamente como los cascos inyectables de los cocientes. R/P Donde P varía sobre el espectro principal del anillo. El casco inyectable R/P como R- El modulo es canónico R_P módulo, y es el R_P- casco inyectable R/P. En otras palabras, basta considerar los anillos locales. El anillo de endomorfismo del casco inyectable R/P es la terminación ${displaystyle {hat {}_{}}} {fn}} {fn}}} {fn}}} {fn}}}}} {fn}}}}} {fn}}}}} {fn}}}}}} {f}}}} {f}}}}}}}}}}}}}}}}}}}}}}}}}}} {$ de R a P.

Dos ejemplos son el casco inyectivo del módulo Z Z/pZ (el grupo Prüfer), y el casco inyectivo del módulo k[x] k (el anillo de polinomios inversos). Este último se describe fácilmente como k[x,x⁻¹]/xk[x]. Este módulo tiene una base que consta de "monomios inversos", es decir, x⁻ⁿ para n = 0, 1, 2,…. La multiplicación por escalares es la esperada y la multiplicación por x se comporta normalmente excepto que x·1 = 0. El anillo de endomorfismo es simplemente el anillo de una serie de potencias formal.

Ejemplos artinianos

Si G es un grupo finito y k un campo con característica 0, entonces se muestra en la teoría de las representaciones de grupos que cualquier subrepresentación de una determinada ya es una suma directa del dado. Traducido al lenguaje de módulo, esto significa que todos los módulos sobre el álgebra de grupo kG son inyectivos. Si la característica de k no es cero, el siguiente ejemplo puede ayudar.

Si A es un álgebra asociativa unital sobre el campo k con dimensión finita sobre k, entonces Hom_k (−, k) es una dualidad entre módulos A izquierdos finitamente generados y A derecho finitamente generados. módulos. Por lo tanto, los módulos A izquierdos inyectivos finitamente generados son precisamente los módulos de la forma Hom_k(P, k) donde P es un módulo proyectivo derecho finitamente generado A. Para las álgebras simétricas, la dualidad se comporta particularmente bien y los módulos proyectivos y los módulos inyectivos coinciden.

Para cualquier anillo artiniano, al igual que para los anillos conmutativos, existe una correspondencia 1-1 entre los ideales primos y los módulos inyectivos indescomponibles. La correspondencia en este caso es quizás incluso más simple: un ideal primo es un aniquilador de un módulo simple único, y el módulo inyectivo indescomponible correspondiente es su cáscara inyectiva. Para álgebras de dimensión finita sobre campos, estos cascos inyectivos son módulos generados de forma finita (Lam 1999, §3G, §3J).

Computación de cascos inyectivos

Si ${displaystyle R.$ es un anillo noetheriano y ${displaystyle {Mathfrak}}$ es un ideal, conjunto ${displaystyle E=E(R/{mathfrak {p})}$ como el casco inyectable. El casco inyectable ${displaystyle R/{mathfrak {p}}$ sobre el anillo Artiniano ${displaystyle R/{Mathfrak {}} {k}}$ puede ser calculado como el módulo ${displaystyle (0:_{E}{mthfrak {} {} {k}}} {fnK}}$. Es un módulo de la misma longitud que ${displaystyle R/{Mathfrak {}} {k}}$. En particular, para el anillo de grado estándar ${displaystyle R_{bullet ¿Qué?$ y ${displaystyle {mathfrak {}=(x_{1},ldotsx_{n}}$, ${displaystyle E=oplus _{i}{text{Hom}(R_{i},k)}$ es un módulo inyectable, dando las herramientas para computar los módulos inyectores indecomposibles para anillos artinianos sobre ${displaystyle k}$.

Autoinyectividad

Anillo local Artin ${displaystyle (R,{mathfrak {m}},K)}$ es inyectable sobre sí mismo si y sólo si ${displaystyle soc(R)}$ es un espacio vectorial de 1 dimensión sobre ${displaystyle K}$. Esto implica que cada anillo local de Gorenstein que es también Artin es inyectable sobre sí mismo desde que tiene un párculo 1-dimensional. Un simple no-ejemplo es el anillo ${displaystyle R=mathbb {C} [x,y]/(x^{2},xy,y^{2}}$ que tiene el ideal máximo ${displaystyle (x,y)}$ y residuos ${displaystyle mathbb {C}$. Su sobrio es ${displaystyle mathbb {C} cdot xoplus mathbb {C} cdot y}$, que es 2-dimensional. El campo de residuos tiene el casco inyectable ${displaystyle {text{Hom}_{mthbb {C}(mathbb {C} cdot xoplus mathbb {C} cdot y,mathbb {C}$.

Módulos sobre álgebras de Lie

Para un álgebra de Lie ${displaystyle {Mathfrak {}}$ sobre un terreno ${displaystyle k}$ de característica 0, la categoría de módulos ${displaystyle {mathcal {} {\fnMithfrak {}}}} {fnMithfrak}} {f}}$ tiene una descripción relativamente sencilla de sus módulos inyectables. Usando el álgebra universal envolviendo cualquier inyección ${displaystyle {Mathfrak {}}$- se puede construir desde el ${displaystyle {Mathfrak {}}$- Mobiliario

${displaystyle {text{Hom}_{k}(U({mathfrak {g}),V)}$

para algunos ${displaystyle k}$- Espacio de vehículos ${displaystyle V}$. Nota este espacio vectorial tiene un ${displaystyle {Mathfrak {}}$- Estructura modulada de la inyección

${displaystyle {Mathfrak {}hookrightarrow U({mathfrak {g}}}$

De hecho, todos ${displaystyle {Mathfrak {}}$- El módulo tiene una inyección en algunos ${displaystyle {text{Hom}_{k}(U({mathfrak {g}),V)}$ y cada inyección ${displaystyle {Mathfrak {}}$- El modulo es un sustituto directo de algunos ${displaystyle {text{Hom}_{k}(U({mathfrak {g}),V)}$.

Teoría

Teorema de estructura para anillos noetherianos conmutativos

Sobre un anillo noetheriano conmutativo ${displaystyle R.$, cada módulo inyectable es una suma directa de módulos inyectables indecomposibles y cada módulo inyector indecomposible es el casco inyectable del campo de residuos en un primer ${displaystyle {Mathfrak}}$. Es decir, para un inyector ${displaystyle Iin {text{Mod}(R)}$ hay un isomorfismo

${displaystyle I 'cong bigoplus ¿Qué?$

Donde ${displaystyle ¿Qué?$ son los cascos inyectables de los módulos ${displaystyle R/{Mathfrak {}_{i}$. Además, si ${displaystyle Yo...$ es el casco inyectable de algún módulo ${displaystyle M}$ entonces el ${displaystyle {Mathfrak {}_{i}$ son los principios asociados de ${displaystyle M}$.

Submódulos, cocientes, productos y sumas

Cualquier producto de (incluso infinitos) módulos inyectivos es inyectivo; por el contrario, si un producto directo de módulos es inyectivo, entonces cada módulo es inyectivo (Lam 1999, p. 61). Toda suma directa de un número finito de módulos inyectivos es inyectiva. En general, los submódulos, módulos de factores o sumas directas infinitas de módulos inyectivos no necesitan ser inyectivos. Cada submódulo de cada módulo inyectivo es inyectivo si y sólo si el anillo es semisimple artiniano (Golan & Head 1991, p. 152); cada módulo factorial de cada módulo inyectivo es inyectivo si y sólo si el anillo es hereditario (Lam 1999, Th. 3.22); toda suma directa infinita de módulos inyectivos es inyectiva si y sólo si el anillo es noetheriano (Lam 1999, Th 3.46).

Criterio de Baer

En el artículo original de Baer, demostró un resultado útil, generalmente conocido como Criterio de Baer, para comprobar si un módulo es inyectivo: un módulo R izquierdo Q es inyectivo si y sólo si hay algún homomorfismo g: I → Q definido en un ideal izquierdo I de R se puede extender a todo R.

Utilizando este criterio, se puede demostrar que Q es un grupo abeliano inyectivo (es decir, un módulo inyectivo sobre Z). De manera más general, un grupo abeliano es inyectivo si y sólo si es divisible. De manera más general aún: un módulo sobre un dominio ideal principal es inyectivo si y sólo si es divisible (el caso de los espacios vectoriales es un ejemplo de este teorema, ya que todo campo es un dominio ideal principal y todo espacio vectorial es divisible). Sobre un dominio integral general, todavía tenemos una implicación: cada módulo inyectivo sobre un dominio integral es divisible.

El criterio de Baer se ha perfeccionado de muchas maneras (Golan & Head 1991, p. 119), incluido el resultado de (Smith 1981) y (Vámos 1983) de que para un anillo noetheriano conmutativo, es suficiente considere sólo los ideales primos I. El dual del criterio de Baer, que daría una prueba de proyectividad, es falso en general. Por ejemplo, el módulo Z Q satisface el criterio dual de Baer pero no es proyectivo.

Cogeneradores inyectivos

Quizás el módulo inyectivo más importante sea el grupo abeliano Q/Z. Es un cogenerador inyectivo en la categoría de grupos abelianos, lo que significa que es inyectivo y cualquier otro módulo está contenido en un producto suficientemente grande de copias de Q/Z. Entonces, en particular, cada grupo abeliano es un subgrupo de uno inyectivo. Es bastante significativo que esto también se aplica a cualquier anillo: cada módulo es un submódulo de uno inyectivo, o "la categoría de módulos R izquierdos tiene suficientes inyectivos". Para probar esto, se utilizan las propiedades peculiares del grupo abeliano Q/Z para construir un cogenerador inyectivo en la categoría de módulos R izquierdos..

Para un módulo R izquierdo M, el llamado "módulo de caracteres" M⁺ = Hom_Z(M,Q/Z) es un módulo R derecho que exhibe una dualidad interesante, no entre módulos inyectivos y módulos proyectivos, sino entre módulos inyectivos y módulos planos (Enochs & Jenda 2000, págs. 78–80). Para cualquier anillo R, un módulo R izquierdo es plano si y sólo si su módulo de carácter es inyectivo. Si R es noetheriano izquierdo, entonces un módulo R izquierdo es inyectivo si y sólo si su módulo de carácter es plano.

Cascos inyectables

La carcasa inyectiva de un módulo es el módulo inyectivo más pequeño que contiene el dado y se describió en (Eckmann & Schopf 1953).

Se pueden utilizar cascos inyectivos para definir una resolución inyectiva mínima (ver más abajo). Si cada término de la resolución inyectiva es la cáscara inyectiva del cokernel del mapa anterior, entonces la resolución inyectiva tiene una longitud mínima.

Resoluciones inyectivas

Cada módulo M también tiene una resolución inyectiva: una secuencia exacta de la forma

0 → M → I⁰ → I¹ → I² →...

donde los I ^j son módulos inyectivos. Las resoluciones inyectivas se pueden utilizar para definir funtores derivados como el functor Ext.

La longitud de una resolución inyectiva finita es el primer índice n tal que Iⁿ es distinto de cero y Iⁱ = 0 para i mayor que n. Si un módulo M admite una resolución inyectiva finita, la longitud mínima entre todas las resoluciones inyectivas finitas de M se denomina dimensión inyectiva y se denota id(M >). Si M no admite una resolución inyectiva finita, entonces por convención se dice que la dimensión inyectiva es infinita. (Lam 1999, §5C) Como ejemplo, considere un módulo M tal que id(M) = 0. En esta situación, la exactitud de la secuencia 0 → < i>M → I⁰ → 0 indica que la flecha en el centro es un isomorfismo y, por lo tanto, M en sí es inyectivo.

Equivalentemente, la dimensión inyectiva de M es el entero mínimo (si existe, en caso contrario ∞) n tal que Ext^N
_A(–,M) = 0 para todos los N > n.

Indecomponibles

Cada submódulo inyectivo de un módulo inyectivo es un sumando directo, por lo que es importante comprender los módulos inyectivos indecomponibles (Lam 1999, §3F).

Cada módulo inyectivo indescomponible tiene un anillo de endomorfismo local. Un módulo se denomina módulo uniforme si cada dos submódulos distintos de cero tienen una intersección distinta de cero. Para un módulo inyectivo M lo siguiente es equivalente:

• M es indecomposible
• M es no cero y es el casco inyectable de cada submodulo no cero
• M uniforme
• M es el casco inyectable de un módulo uniforme
• M es el casco inyectable de un módulo cíclico uniforme
• M tiene un anillo de endomorfismo local

Sobre un anillo noetheriano, cada módulo inyectivo es la suma directa de módulos inyectivos indescomponibles (determinados de forma única). Sobre un anillo noetheriano conmutativo, esto proporciona una comprensión particularmente agradable de todos los módulos inyectivos, descritos en (Matlis 1958). Los módulos inyectivos indescomponibles son las cáscaras inyectivas de los módulos R/p para p un ideal primo del anillo R. Además, el casco inyectable M de R/p tiene una filtración creciente por módulos M_n dado por los aniquiladores de los ideales pⁿ, y M _n+1/M_n es isomorfo como espacio vectorial de dimensión finita sobre el campo cociente k(p) de R/p a Hom_R/p(pⁿ/pⁿ⁺¹, k(p)).

Cambio de anillos

Es importante poder considerar módulos sobre subanillos o anillos cocientes, especialmente, por ejemplo, anillos polinomiales. En general, esto es difícil, pero se conocen varios resultados (Lam 1999, p. 62).

Sean S y R anillos, y P sea una R izquierda, una S bimódulo que es plano como un módulo R izquierdo. Para cualquier módulo inyectivo derecho S M, el conjunto de homomorfismos de módulo Hom_S(P, M) es un módulo R derecho inyectivo. La misma afirmación es válida, por supuesto, después de intercambiar los atributos izquierdo y derecho.

Por ejemplo, si R es un subanillo de S tal que S es un módulo R plano, entonces cada módulo inyectivo S es un módulo inyectivo R. En particular, si R es un dominio integral y S su campo de fracciones, entonces todo espacio vectorial sobre S es un R inyectivo. -módulo. De manera similar, cada módulo inyectivo R[x] es un módulo inyectivo R.

En la dirección opuesta, un homomorfismo de anillo ${displaystyle f:Sto R}$ # R en una izquierda...R, derecha-S bimodulo, por multiplicación izquierda y derecha. Ser libre sobre sí mismo R es también plana como una izquierda R- Bien. Especialización de la declaración mencionada P = R, dice que cuando M es un derecho inyectable S-module el módulo coducido ${displaystyle F_{*}M=mathrm ¿Qué?$ es un derecho inyectable R- Bien. Así, coinducción sobre f produce inyección R-módulos de inyección S-módulos.

Para los anillos de cociente R/I, el cambio de anillos también es muy claro. Un módulo R es un módulo R/I precisamente cuando es aniquilado por I. El submódulo ann_I(M) = { m en M: im = 0 para todo i en I } es un submódulo izquierdo del módulo R izquierdo M, y es el submódulo más grande de M que es un módulo R/I. Si M es un módulo R izquierdo inyectivo, entonces ann_I(M) es un módulo inyectivo izquierdo R/I. Aplicando esto a R=Z, I=nZ y M=Q/Z, uno se da cuenta de que Z/n Z es inyectivo como un módulo sobre sí mismo. Si bien es fácil convertir módulos R inyectivos en módulos R/I inyectivos, este proceso no convierte el R< inyectivo /i>-resoluciones en inyectivas R/I-resoluciones, y la homología del complejo resultante es una de las primeras y fundamentales áreas de estudio del álgebra homológica relativa.

El libro de texto (Rotman 1979, p. 103) tiene una prueba errónea de que la localización preserva los inyectivos, pero en (Dade 1981) se dio un contraejemplo.

Anillos autoinyectivos

Cada anillo con unidad es un módulo libre y por lo tanto es proyectivo como módulo sobre sí mismo, pero es más raro que un anillo sea inyectivo como módulo sobre sí mismo (Lam 1999, §3B). Si un anillo es inyectivo sobre sí mismo como módulo derecho, entonces se llama anillo autoinyectivo derecho. Todo álgebra de Frobenius es autoinyectivo, pero ningún dominio integral que no sea un campo es autoinyectivo. Todo cociente propio de un dominio de Dedekind es autoinyectivo.

Un anillo noetheriano derecho, autoinyectivo derecho, se llama anillo cuasi-Frobenius y es artiniano de dos caras e inyectivo de dos caras (Lam 1999, Th. 15.1). Una propiedad teórica de módulo importante de los anillos cuasi-Frobenius es que los módulos proyectivos son exactamente los módulos inyectivos.

Generalizaciones y especializaciones

Objetos inyectivos

También se habla de objetos inyectivos en categorías más generales que las categorías de módulos, por ejemplo en categorías de functores o en categorías de haces de módulos O_X sobre algún espacio anillado. (X,O_X). Se utiliza la siguiente definición general: un objeto Q de la categoría C es inyectivo si para cualquier monomorfismo f: X → Y en C y cualquier morfismo g: X → Q existe un morfismo h: Y → Q con hf = g.

Grupos divisibles

La noción de objeto inyectivo en la categoría de grupos abelianos se estudió de manera algo independiente de los módulos inyectivos bajo el término grupo divisible. Aquí un módulo Z M es inyectivo si y sólo si n⋅M = M para cada entero n distinto de cero. Aquí las relaciones entre módulos planos, submódulos puros y módulos inyectivos son más claras, ya que simplemente se refieren a ciertas propiedades de divisibilidad de los elementos del módulo por números enteros.

Inyectivas puras

En álgebra homológica relativa, la propiedad de extensión de los homomorfismos puede ser necesaria sólo para ciertos submódulos, en lugar de para todos. Por ejemplo, un módulo inyectivo puro es un módulo en el que un homomorfismo de un submódulo puro se puede extender al módulo completo.