Módulo de corte

En ciencia de materiales, módulo de corte o módulo de rigidez, denotado por G, o a veces S o μ, es una medida de la rigidez cortante elástica de un material y se define como la relación entre el esfuerzo cortante y la deformación cortante:
- G =def τ τ xSí.γ γ xSí.=F/AΔ Δ x/l=FlAΔ Δ x{displaystyle G {fnK} {fnK} {fnh} {fnh}} {fnh}} {fn}}} {fn}}}}\fn}\fn}\fnfn}\\\fn}\\fnKfnKcH0}}}\\\\fn}}\\\\\\\\\\\\\\fn}\\\\\\\\\\fn}\\\\\\\\\\\\\fn}\\\\\\\\\fn}\\fn}\\fn}\\\\cHFF}\cHFF}\\\ {fnMicroc} ¿Por qué? {fnK}= {fnMicroc {fnK}} {fnMicroc {f} {Delta x}}}}
dónde
- τ τ xSí.=F/A{displaystyle tau _{xy}=F/A,} = estrés de derrame
- F{displaystyle F} es la fuerza que actúa
- A{displaystyle A} es la zona en que la fuerza actúa
- γ γ xSí.{displaystyle gamma _{xy}} = escarpada. En ingeniería :=Δ Δ x/l=# Silencio Silencio {displaystyle:= Delta x/l=tan theta }, en otros lugares :=Silencio Silencio {displaystyle:=theta }
- Δ Δ x{displaystyle Delta x} es el desplazamiento transversal
- l{displaystyle l} es la longitud inicial de la zona.
La unidad SI derivada del módulo de corte es el pascal (Pa), aunque generalmente se expresa en gigapascals (GPa) o en mil libras por pulgada cuadrada (ksi). Su forma dimensional es M1L−1T−2, sustitución fuerza por masa veces aceleración.
Explicación
| Material | Valores típicos para shear modulus (GPa) (a temperatura ambiente) |
|---|---|
| Diamante | 478.0 |
| Acero | 79.3 |
| Iron | 52,5 |
| Copper | 44,7 |
| Titanio | 41,4 |
| Cristal | 26.2 |
| Aluminio | 25,5 |
| Polietileno | 0.117 |
| Rubber | 0,0006 |
| Granito | 24 |
| Shale | 1.6 |
| Limestone | 24 |
| Chalk | 3.2 |
| Sandstone | 0,4 |
| Madera | 4 |
El módulo es una de varias cantidades para medir la rigidez de los materiales. Todos ellos surgen en la ley generalizada de Hooke:
- El módulo de Young E describe la respuesta de la tensión del material al estrés uniaxial en la dirección de este estrés (como tirar en los extremos de un alambre o poner un peso en la parte superior de una columna, con el alambre se hace más largo y la columna perdiendo altura),
- la relación de Poisson . describe la respuesta en las direcciones ortogonales a este estrés uniaxial (el alambre se hace más delgado y la columna más gruesa),
- el módulo de vracs K describe la respuesta del material a la presión hidrostática (uniforme) (como la presión en la parte inferior del océano o una piscina profunda),
- el shear modulus G describe la respuesta del material al estrado de estrés (como cortarlo con tijeras aburridas).
Estos módulos no son independientes y, para materiales isotrópicos, están conectados mediante las ecuaciones
- E=2G()1+. . )=3K()1− − 2. . ){displaystyle E=2G(1+nu)=3K(1-2nu)}
El módulo de corte tiene que ver con la deformación de un sólido cuando experimenta una fuerza paralela a una de sus superficies mientras su cara opuesta experimenta una fuerza opuesta (como la fricción). En el caso de un objeto con forma de prisma rectangular, se deformará formando un paralelepípedo. Los materiales anisotrópicos como la madera, el papel y también esencialmente todos los monocristales exhiben diferentes respuestas del material a la tensión o deformación cuando se prueban en diferentes direcciones. En este caso, es posible que sea necesario utilizar la expresión tensorial completa de las constantes elásticas, en lugar de un único valor escalar.
Una posible definición de fluido sería un material con módulo de corte cero.
Ondas de corte

En sólidos homogéneos e isotrópicos, hay dos tipos de ondas, ondas de presión y ondas de derrame. La velocidad de una onda de ola, ()vs){displaystyle (v_{s})} es controlado por el módulo de tijera,
- vs=G*** *** {displaystyle {fnK} {fnMicroc {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {f} {fnMicroc} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft}} {fnMicrosoft}}} {f}f}}}}}}f}}}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}f}\f}f}f}f}f}f}f}f}f}fnf}f}f}f}f}fnh}fnhf}fnf}f}f}f}f}fn }
dónde
- G es el módulo de corte
- *** *** {displaystyle rho } es la densidad del sólido.
Módulo de corte de los metales
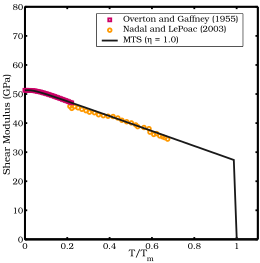
Por lo general, se observa que el módulo de corte de los metales disminuye al aumentar la temperatura. A altas presiones, el módulo de corte también parece aumentar con la presión aplicada. En muchos metales se han observado correlaciones entre la temperatura de fusión, la energía de formación de vacantes y el módulo de corte.
Existen varios modelos que intentan predecir el módulo de corte de los metales (y posiblemente el de las aleaciones). Los modelos de módulo de corte que se han utilizado en cálculos de flujo plástico incluyen:
- el modelo de módulo de corte MTS desarrollado por y utilizado en conjunto con el modelo de tensión de flujo de plástico Mechanical Threshold (MTS).
- el modelo Steinberg-Cochran-Guinan (SCG) Shear modulus desarrollado y utilizado en conjunto con el modelo de tensión de flujo Steinberg-Cochran-Guinan-Lund (SCGL).
- el modelo Nadal y LePoac (NP) shear modulus que utiliza la teoría de Lindemann para determinar la dependencia de temperatura y el modelo SCG para la dependencia de presión del módulo de tijera.
Modelo MTS
El modelo de módulo de corte MTS tiene la forma:
- μ μ ()T)=μ μ 0− − Dexp ()T0/T)− − 1{displaystyle mu (T)=mu ¿Por qué?
Donde μ μ 0{displaystyle mu _{0}} es el módulo del tirón T=0K{displaystyle T=0K}, y D{displaystyle D} y T0{displaystyle T_{0} son constantes materiales.
Modelo SCG
El modelo de módulo de corte de Steinberg-Cochran-Guinan (SCG) depende de la presión y tiene la forma
- μ μ ()p,T)=μ μ 0+∂ ∂ μ μ ∂ ∂ pp. . 13+∂ ∂ μ μ ∂ ∂ T()T− − 300);. . :=*** *** *** *** 0{displaystyle mu (p,T)=mu {fnK} {fnMicrosoft } {fnMicrosoft } {fnMicrosoft } {1}{3}}}}}+{frac {partial mu }{partial T} {f-300);quad eta:={frac {rho }{rho ♪♪
donde, μ0 es el módulo de corte en el estado de referencia (T = 300 K, p = 0, η = 1) , p es la presión y T es la temperatura.
Modelo NP
El modelo de módulo de corte de Nadal-Le Poac (NP) es una versión modificada del modelo SCG. La dependencia empírica de la temperatura del módulo de corte en el modelo SCG se reemplaza con una ecuación basada en la teoría de fusión de Lindemann. El modelo del módulo de corte NP tiene la forma:
- μ μ ()p,T)=1J()T^ ^ )[()μ μ 0+∂ ∂ μ μ ∂ ∂ pp. . 13)()1− − T^ ^ )+*** *** Cm T];C:=()6π π 2)233f2{displaystyle mu (p,T)={frac {1}{mathcal {J}left({hat {}right)}left[left(mu] {fnK} {fnMicrosoft } {fnMicrosoft } {fnMicrosoft } {1}{3}}}right)left(1-{hat {T}right)+{frac {rho }{Cm}~Tright];quad C:={frac {left(6pi ^{2}right)^{frac {2} {3}}} {2}} {2}}}} {3}}}} {3}}}} {}} {2}}}} {2}}}}}}}}}} {}}} {}}} {}}} {}}} {}}}}}} {}}}}}} {}}}}}}} {}}}}} {}}} {}}}}}}}}} {}}}}}}} {}}}} {}}}}}}}}}}} {}}}}} {} {}}}}}} {} {}}}} {}}}} {}}}}}}}}}}}}}}}} {} {} {}}}} {}}}}}} {}}}}}} {}}}}}} {}}}}}} {}}}}}}}}}}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}
dónde
- J()T^ ^ ):=1+exp [− − 1+1/Especificaciones Especificaciones 1+Especificaciones Especificaciones /()1− − T^ ^ )]paraT^ ^ :=TTm▪ ▪ [0,6+Especificaciones Especificaciones ],{fnMicrosoft} {T}):=1+exp left[-{frac {1+1/zeta }{1+zeta /left(1-{hat {T}right)}derecha]quad {text{for}quad}quad [0,6+zeta]
y μ0 es el módulo de cierre a cero absoluto y la presión ambiente, ♥ es un área, m es la masa atómica, y f es la constante de Lindemann.
Molimento de relajación de ojeras
El módulo de relajación G()t){displaystyle G(t)} es la generalización dependiente del tiempo del módulo de hídrido G{displaystyle G.:
- G=limt→ → JUEGO JUEGO G()t){displaystyle G=lim _{tto infty }G(t)}.
Contenido relacionado
Julio (unidad)
Pascal (unidad)
Precisión y exactitud



















![{displaystyle mu (p,T)={frac {1}{{mathcal {J}}left({hat {T}}right)}}left[left(mu _{0}+{frac {partial mu }{partial p}}{frac {p}{eta ^{frac {1}{3}}}}right)left(1-{hat {T}}right)+{frac {rho }{Cm}}~Tright];quad C:={frac {left(6pi ^{2}right)^{frac {2}{3}}}{3}}f^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a44071b746c80d284fb8d0e0f1ac54b8b3e1d20)
![{displaystyle {mathcal {J}}({hat {T}}):=1+exp left[-{frac {1+1/zeta }{1+zeta /left(1-{hat {T}}right)}}right]quad {text{for}}quad {hat {T}}:={frac {T}{T_{m}}}in [0,6+zeta ],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1eaa94198fcbeba0ea126aea1b4e743ce62f1c4)


