Modulación delta-sigma

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Método para convertir señales entre digital y analógico

Modulación sincrónica de 1 bit (azul) de una onda sine (rojo).

Delta-sigma ()Δena; o sigma-delta, CEPAL) modulación es un método de sobre muestreo para la codificación de señales en señales digitales de baja profundidad de bits a una frecuencia de muestra muy alta como parte del proceso de conversores analógicos delta-sigma (ADCs) y convertidores digitales-a-analógico (DACs). La modulación Delta-sigma logra una alta calidad utilizando un bucle de retroalimentación negativa durante la cuantificación a la profundidad inferior de bits que corrige continuamente errores de cuantificación y mueve el ruido de cuantización a frecuencias superiores muy por encima del ancho de banda original de la señal. El filtrado de baja velocidad posterior para la demodulación elimina fácilmente este ruido de alta frecuencia y promedios de tiempo para lograr una alta precisión en amplitud que puede ser codificado en última instancia como modulación de código de pulso (PCM).

Tanto los ADC como los DAC pueden emplear modulación delta-sigma. Un ADC delta-sigma (por ejemplo, Figura 1 arriba) codifica una señal analógica usando modulación delta-sigma de alta frecuencia y luego aplica un filtro digital para demodularla a una salida digital de bits altos a una frecuencia de muestreo más baja. Un DAC delta-sigma (por ejemplo, la Figura 1 inferior) codifica una señal de entrada digital de alta resolución en una señal de frecuencia de muestra más baja pero más alta que luego puede asignarse a voltajes y suavizarse con un filtro analógico para demodulación. En ambos casos, el uso temporal de una señal de baja profundidad de bits a una frecuencia de muestreo más alta simplifica el diseño del circuito y aprovecha la eficiencia y alta precisión en el tiempo de la electrónica digital.

Principalmente debido a su rentabilidad y complejidad reducida de los circuitos, esta técnica se ha utilizado cada vez más en componentes electrónicos modernos como DAC, ADC, sintetizadores de frecuencia, fuentes de alimentación de modo conmutado y controladores de motores. La salida cuantificada de forma aproximada de un ADC delta-sigma se utiliza ocasionalmente directamente en el procesamiento de señales o como representación para el almacenamiento de señales (por ejemplo, Super Audio CD almacena la salida sin procesar de un modulador delta-sigma de 1 bit).

Si bien este artículo se centra en la modulación síncrona, que requiere un reloj preciso para la cuantificación, la modulación delta-sigma asíncrona se ejecuta sin reloj.

Motivación

Cuando se transmite una señal analógica directamente, todo el ruido en el sistema y la transmisión se agrega a la señal analógica, lo que reduce su calidad. Digitalizarlo permite una transmisión, almacenamiento y procesamiento sin ruidos. Existen muchos métodos de digitalización.

En los ADC de frecuencia Nyquist, una señal analógica se muestrea a una frecuencia de muestreo relativamente baja, justo por encima de su frecuencia Nyquist (el doble de la frecuencia más alta de la señal) y se cuantifica mediante un cuantificador multinivel para producir una frecuencia multibit. señal digital. Estos métodos de bits más altos buscan precisión en la amplitud directamente, pero requieren componentes extremadamente precisos y, por lo tanto, pueden adolecer de una linealidad deficiente.

Ventajas del sobremuestreo

En cambio, los convertidores de sobremuestreo producen un resultado con una profundidad de bits más baja a una frecuencia de muestreo mucho más alta. Esto puede lograr una calidad comparable aprovechando:

Mayor precisión en el tiempo (asegurado por circuitos digitales de alta velocidad y relojes altamente precisos).
La linealidad más alta proporcionada por ADCs de bajo nivel y DACs (por ejemplo, un DAC de 1 bit que sólo produce dos valores de un alto voltaje preciso y una baja tensión precisa es perfectamente lineal, en principio).
Forma de ruido: mover el ruido a las frecuencias superiores por encima de la señal de interés, por lo que se pueden eliminar fácilmente con filtro de baja velocidad.
Requisito de empinado reducido para los filtros analógicos anti-aliasing. Los filtros de alto orden con una banda plana cuestan más en el dominio analógico que en el dominio digital.

Compensación frecuencia/resolución

Otro aspecto clave dado por el sobremuestreo es el equilibrio entre frecuencia y resolución. El filtro de diezmado colocado después del modulador no solo filtra toda la señal muestreada en la banda de interés (cortando el ruido en frecuencias más altas), sino que también reduce la frecuencia de muestreo y, por lo tanto, el rango de frecuencia representable de la señal, al tiempo que aumenta la muestra. resolución de amplitud. Esta mejora en la resolución de amplitud se obtiene mediante una especie de promediado del flujo de bits de mayor velocidad de datos.

Mejora sobre la modulación delta

La modulación delta es un método anterior de sobremuestreo de bits bajos relacionado que también utiliza retroalimentación negativa. Pero la modulación delta sólo codifica la derivada de la señal (su delta) en lugar de su amplitud, por lo que es incapaz de transportar el componente CC de la señal y es susceptible a perturbaciones en la transmisión que resultan en interferencias acumulativas. error. El resultado es una corriente de pulsos que representan el movimiento hacia arriba o hacia abajo de la señal, que deben integrarse para reconstruir la amplitud de la señal. La modulación delta sufre una sobrecarga de pendiente si las señales se mueven demasiado rápido. Su rango dinámico y SNR son inversamente proporcionales a la frecuencia de la señal,

La modulación delta-sigma reorganiza el integrador y el cuantificador de un modulador delta, de modo que la salida transporta información correspondiente a la amplitud de la señal de entrada en lugar de solo su derivada. Esto también tiene la ventaja de incorporar una configuración de ruido deseable en el proceso de conversión, para mover deliberadamente el ruido de cuantificación a frecuencias más altas que la señal. Dado que la señal de error acumulada es filtrada en paso bajo por el integrador del modulador delta-sigma antes de ser cuantificada, la retroalimentación negativa posterior de su resultado cuantificado resta efectivamente los componentes de baja frecuencia del ruido de cuantificación y deja los componentes de frecuencia más alta del ruido. .

La modulación delta-sigma de 1 bit es modulación de densidad de pulso

En el caso específico de un ADC ΔΣ síncrono de un solo bit, una señal de voltaje analógica se convierte efectivamente en una frecuencia de pulso, o densidad de pulso, que puede entenderse como modulación de densidad de pulso (PDM). Una secuencia de pulsos positivos y negativos, que representan bits a una velocidad fija conocida, es muy fácil de generar, transmitir y regenerar con precisión en el receptor, siempre que se pueda recuperar la temporización y el signo de los pulsos. Dada una secuencia de pulsos de un modulador delta-sigma, la forma de onda original puede reconstruirse con la precisión adecuada.

El uso de PDM como representación de señal es una alternativa al PCM. Alternativamente, el PDM de alta frecuencia se puede reducir posteriormente mediante un proceso llamado diezmado y recuantificarlo para convertirlo en un código PCM de múltiples bits a una frecuencia de muestreo más baja y más cercana a la tasa de Nyquist de la banda de frecuencia de interés.

Historia y variaciones

El artículo fundamental que combina la retroalimentación con el sobremuestreo para lograr la modulación delta fue el de F. de Jager de Philips Research Laboratories en 1952.

El principio de mejorar la resolución de un cuantificador aproximado mediante el uso de retroalimentación, que es el principio básico de la conversión delta-sigma, fue descrito por primera vez en una patente presentada en 1954 por C. Chapin Cutler de Bell Labs. No fue nombrado como tal hasta un artículo de 1962 de Inose et al. de la Universidad de Tokio, a quien se le ocurrió la idea de agregar un filtro en el camino directo del modulador delta.

El libro "La evolución de los convertidores analógicos a digitales con sobremuestreo" ofrece más historia y referencias a patentes relevantes. Algunas vías de variación (que pueden aplicarse en diferentes combinaciones) son el orden del modulador, la profundidad de bits del cuantificador, la forma de diezmado y la relación de sobremuestreo.

Modulador de orden superior

La configuración del ruido se mejora conectando en cascada múltiples etapas integradoras, cuyo número indica el orden de un modulador ΔΣ (por ejemplo, la Figura 2 es un modulador de segundo orden) .

Los moduladores de

primer orden son incondicionalmente estables, pero se debe realizar un análisis de estabilidad para los moduladores de retroalimentación de ruido de orden superior. Alternativamente, las configuraciones de retroalimentación de ruido son siempre estables y tienen un análisis más simple.^§6.1

Cuantizador multibit

El modulador también se puede clasificar por la profundidad de bits de su cuantificador. Un cuantificador que distingue entre N niveles se denomina cuantificador de log₂N bits. Por ejemplo, un comparador simple tiene 2 niveles y también lo es un cuantificador de 1 bit; un cuantificador de 3 niveles se llama "1.5" cuantificador de bits; un cuantificador de 4 niveles es un cuantificador de 2 bits; un cuantificador de 5 niveles se llama cuantificador de 2,5 bits. Los cuantificadores de bits más altos producen inherentemente menos ruido de cuantificación.

Una crítica a la cuantificación de 1 bit es que no se pueden usar cantidades adecuadas de dither en el bucle de retroalimentación, por lo que se puede escuchar distorsión en algunas condiciones (más discusión en Direct Stream Digital § DSD vs. PCM).

Aniquilación posterior

La diezmación está fuertemente asociada con la modulación delta-sigma, pero es distinta y está fuera del alcance de este artículo. El artículo original de 1962 no describía la aniquilación. Los datos sobremuestreados en los primeros días se enviaron tal cual. La propuesta de diezmar los datos delta-sigma sobremuestreados mediante filtrado digital antes de convertirlos en audio PCM fue realizada por D. J. Goodman en Bell Labs en 1969, para reducir la señal ΔΣ de su alta frecuencia de muestreo y al mismo tiempo aumentar su profundidad de bits. El diezmado se puede realizar en un chip separado en el extremo receptor del flujo de bits delta-sigma, a veces mediante un módulo dedicado dentro de un microcontrolador, que es útil para interactuar con micrófonos PDM MEMS, aunque muchos circuitos integrados ΔΣ ADC incluyen diezmado. Algunos microcontroladores incluso incorporan tanto el modulador como el diezmador.

Los filtros de diezmado más comúnmente utilizados para ΔΣ ADC, en orden de complejidad y calidad crecientes, son:

Filtro promedio móvil de Boxcar (promedio móvil simple o sinc-en-frecuencia o sinc¹ Filtro: Este es el filtro digital más fácil y conserva una respuesta rápida, pero es mediocre al separar bandas de frecuencia y sufre de distorsión intermodulatoria. El filtro se puede implementar simplemente contando cuántas muestras durante un intervalo de muestreo más grande son altas. El documento de 1974 de otro investigador de Bell Labs, J. C. Candy, "Un uso de oscilaciones de ciclos límite para obtener los conversores analógicos a digitales" fue uno de los primeros ejemplos de esto.
Filtros Cascaded integrador-comb: Estos son llamados sinc^N filtros, equivalentes a la cascada del seno anterior¹ Filtro N veces y reorganización del orden de operaciones para la eficiencia computacional. Bajo Los filtros N son más simples, se instalan más rápido y tienen menos atenuación en la banda base, mientras que los filtros N más altos son un poco más complejos y se establecen más lentos y tienen más droop en la banda, pero mejor atenuar el ruido de alta frecuencia no deseado. Sin embargo, se pueden aplicar filtros de compensación para contrarrestar la atenuación no deseada de la banda. Sinc^N Los filtros son adecuados para la modulación de sigma delta decimating hasta cuatro veces la tasa de Nyquist. La altura de la primera carga lateral es -13·N dB y la altura de los lóbulos sucesivos caen gradualmente, pero sólo las áreas alrededor de los nulls se alian a la banda de baja frecuencia de interés; por ejemplo, cuando el downsampling por 8, el mayor aliased componente de alta frecuencia puede ser -16 dB debajo del pico de la banda de interés con un sinc¹ filtro pero -40 dB abajo para un sinc³ filtro, y si sólo interesado en un ancho de banda más estrecho, incluso menos componentes de alta frecuencia se alia en él (ver Figuras 7-9 del artículo de Lyon).
Filtros sinc-in-time (brick-wall en frecuencia): Aunque el soporte infinito de la función sinc evita que sea realizable en tiempo finito, la función sinc se puede ventanar para realizar filtros de respuesta de impulso finito. Este diseño de filtro aproximado, manteniendo casi no atenuación de la banda de menor frecuencia de interés, todavía elimina casi todo ruido de alta frecuencia. La desventaja es un mal desempeño en el dominio del tiempo (por ejemplo, la respuesta paso a paso y la onda), mayor retraso (es decir, su tiempo de convolución es inversamente proporcional a su empinada de transición de corte), y mayores requisitos computacionales. Son el estándar de facto para los convertidores digitales de audio de alta fidelidad.

Reducción del ruido de banda base aumentando la relación de sobremuestreo y el orden ΔΣM

Cuando se cuantifica una señal, la señal resultante puede ser aproximada por adición de ruido blanco con una intensidad aproximadamente igual en todo el espectro. En realidad, el ruido de cuantificación es, por supuesto, no independiente de la señal y esta dependencia resulta en ciclos límite y es la fuente de tonos ociosos y ruido de patrón en los convertidores delta-sigma. Sin embargo, la adición de ruido de dispersión (Figura 3) reduce tal distorsión haciendo que el ruido de cuarentena sea más aleatorio.

Los ADC ΔΣ reducen la cantidad de este ruido en la banda base distribuyéndolo y dándole forma para que esté principalmente en frecuencias más altas. Luego se puede filtrar fácilmente con filtros digitales económicos, sin los circuitos analógicos de alta precisión que necesitan los ADC Nyquist.

Sobremuestreo para distribuir el ruido de cuantificación

El ruido de cuantificación en el rango de frecuencia de banda base (de DC a DC) ${displaystyle 2f_{0}}$ ) puede reducirse aumentando la relación de sobresampling (OSR) definida por

{displaystyle mathrm {OSR} ,=,{frac {f_{s}}{2f_{0}}}=2^{d}}

Donde ${displaystyle f_{mathrm {s} }}$ es la frecuencia de muestreo y ${displaystyle 2f_{0}}$ es la tasa de Nyquist (la tasa mínima de muestreo necesaria para evitar el aliado, que es el doble de la frecuencia máxima de la señal original ${displaystyle f_{0}}$ ). Puesto que el oversampling se hace normalmente en poderes de dos, ${displaystyle d}$ representa cuántas veces se duplica el OSR.

Figura 4: Cobertura de ruido curvas y espectro de ruido en 1^st, 2^nd, y 3^rd-order moduladores Δega.

Como se ilustra en la Figura 4, la cantidad total de ruido de cuantificación es la misma tanto en un convertidor Nyquist (áreas amarillas + verdes) como en un convertidor de sobremuestreo (áreas azules + verdes). Pero los convertidores de sobremuestreo distribuyen ese ruido en un rango de frecuencia mucho más amplio. El beneficio es que la cantidad total de ruido en la banda de frecuencia de interés es dramáticamente menor para los convertidores de sobremuestreo (solo la pequeña área verde) que para un convertidor Nyquist (área total amarilla + verde).

Formación de ruido

La Figura 4 muestra cómo la modulación ΔΣ da forma al ruido para reducir aún más la cantidad de ruido de cuantificación en la banda base a cambio de aumentar el ruido en frecuencias más altas (donde se puede filtrar fácilmente). Las curvas de los moduladores ΔΣ de orden superior logran una reducción aún mayor del ruido en la banda base.

Estas curvas se derivan usando herramientas matemáticas llamadas la transformación de Laplace (para señales de tiempo continuo, por ejemplo en el bucle de modulación de ADC) o la Z-transform (para señales discretas de tiempo, por ejemplo en el bucle de modulación de DAC). Estos transformados son útiles para convertir matemáticas más duras del dominio del tiempo en matemáticas más simples en el dominio de frecuencia compleja de la variable compleja ${displaystyle {text{s}}=sigma +jomega }$ (en el dominio Laplace) o ${displaystyle {text{z}}=Ae^{jphi }}$ (en el dominio z). Tal notación es la lingua franca del procesamiento digital de señales, pero no es comprensible por los laicos.

Análisis del bucle de modulación ΔΣ ADC en el dominio de Laplace

La Figura 5 representa el bucle de modulación ΔΣ ADC de primer orden (de la Figura 1) como un sistema lineal de tiempo continuo invariante en el tiempo en el dominio de Laplace con la ecuación:

{displaystyle [{text{in}}({text{s}})-Delta Sigma {text{M}}({text{s}})]cdot {frac {1}{text{s}}}+{text{noise}}({text{s}})=Delta Sigma {text{M}}({text{s}}),.}

La transformación de Laplace de la integración de una función del tiempo corresponde a la simple multiplicación por ${displaystyle {tfrac {1}{text{s}}}}$ en Laplace notation. Se supone que el integrador es un integrador ideal para mantener la matemática simple, pero un integrador real (o filtro similar) puede tener una expresión más complicada.

El proceso de cuantificación se aproxima como una suma con una fuente de ruido de error de cuantificación. A menudo se supone que el ruido es blanco e independiente de la señal, aunque, como explica la cuantificación (procesamiento de señales) § Modelo de ruido aditivo, no siempre es una suposición válida (particularmente para la cuantificación de bits bajos).

Dado que el sistema y la transformada de Laplace son lineales, el comportamiento total de este sistema se puede analizar separando cómo afecta la entrada de cómo afecta el ruido:^§6

{displaystyle Delta Sigma {text{M}}_{text{total}}({text{s}})=Delta Sigma {text{M}}_{text{in}}({text{s}})+Delta Sigma {text{M}}_{text{noise}}({text{s}}),.}

Filtro de paso bajo en la entrada

Para comprender cómo el sistema afecta solo la señal de entrada, se imagina temporalmente que el ruido es 0:

{displaystyle [{text{in}}({text{s}})-Delta Sigma {text{M}}_{text{in}}({text{s}})]cdot {frac {1}{text{s}}}+0=Delta Sigma {text{M}}_{text{in}}({text{s}}),,}

que se puede reorganizar para producir la siguiente función de transferencia:

{displaystyle {frac {Delta Sigma {text{M}}_{text{in}}({text{s}})}{{text{in}}({text{s}})}}={frac {tfrac {1}{text{s}}}{1+{tfrac {1}{text{s}}}}}={frac {1}{{text{s}}+1}},.}

Esta función de transferencia tiene un único polo en ${displaystyle {text{s}}={text{-1}}}$ en el plano complejo, por lo que actúa eficazmente como 1^st-orden filtro de paso bajo en la señal de entrada. (Nota: su frecuencia de corte puede ser ajustada según se desee incluyendo la multiplicación por una constante en el bucle).

Filtro de paso alto sobre ruido

Para comprender cómo el sistema afecta únicamente al ruido, se imagina temporalmente que la entrada es 0:

{displaystyle [0-Delta Sigma {text{M}}_{text{noise}}({text{s}})]cdot {frac {1}{text{s}}}+{text{noise}}({text{s}})=Delta Sigma {text{M}}_{text{noise}}({text{s}}),,}

que se puede reorganizar para producir la siguiente función de transferencia:

{displaystyle {frac {Delta Sigma {text{M}}_{text{noise}}({text{s}})}{{text{noise}}({text{s}})}}={frac {1}{1+{tfrac {1}{text{s}}}}}={frac {s}{{text{s}}+1}},.}

Esta función de transferencia tiene un solo cero ${displaystyle {text{s}}=0}$ y un poste en ${displaystyle {text{s}}={text{-1}},}$ por lo que el sistema actúa eficazmente como un filtro de alto paso en el ruido que comienza en 0 en DC, luego aumenta gradualmente hasta que alcanza la frecuencia de corte, y luego los niveles apagados.

Análisis de bucle de modulación Δega sincrónico en z-dominio

Mientras tanto, el bucle de modulación del ΔΣ DAC síncrono (Figura 6) es en tiempo discreto y, por lo tanto, su análisis se realiza en el dominio z. Es muy similar al análisis anterior en el dominio de Laplace y produce curvas similares. Nota: muchas fuentes^§6.1 también analizan un bucle de modulación de ΔΣ ADC en el dominio z, que implícitamente trata la entrada analógica continua como una señal de tiempo discreto. Esta puede ser una aproximación válida siempre que la señal de entrada ya tenga una banda limitada y se pueda suponer que no cambia en escalas de tiempo superiores a la frecuencia de muestreo. Es particularmente apropiado cuando el modulador se implementa como un circuito capacitor conmutado, que funciona transfiriendo carga entre capacitores en pasos de tiempo cronometrados.

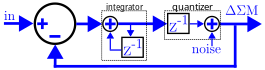
La integración en tiempo discreto puede ser un acumulador que resume repetidamente su entrada ${displaystyle x[n]}$ con el resultado anterior de su suma ${displaystyle y[n]=x[n]+y[n-1].}$ Esto está representado en el dominio z alimentando la salida de un nodo de rebote ${displaystyle y({text{z}})}$ a 1 hora de retraso del ciclo (anotado como ${displaystyle {text{z}}^{text{-1}}}$ ) en otra entrada del nodo de adelgazamiento, rindiendo ${displaystyle y({text{z}})=x({text{z}})+y({text{z}})cdot {text{z}}^{text{-1}}}$ . Su función de transferencia ${displaystyle {tfrac {1}{1-{text{z}}^{text{-1}}}}}$ a menudo se utiliza para etiquetar integradores en diagramas de bloques.

En un DAC de Δxia, el cuantizador puede llamarse un requantizer o a convertidor digital a digital (DDC), debido a que su entrada ya es digital y cuantificada, pero está simplemente reduciendo de una señal digital más profunda a una menor profundidad. Esto está representado en el dominio z por otro ${displaystyle {text{z}}^{text{-1}}}$ etapa de retraso en serie con la adición de ruido de cuarentena. (Nota: algunas fuentes pueden haber cambiado el orden del ${displaystyle {text{z}}^{text{-1}}}$ y etapas de ruido aditivo.)

La ecuación de dominio z del modulador dispuesta como la Figura 6 es:

{displaystyle [{text{in}}({text{z}})-Delta Sigma {text{M}}({text{z}})]cdot {frac {1}{1-{text{z}}^{text{-1}}}}cdot {text{z}}^{text{-1}}+{text{noise}}({text{z}})=Delta Sigma {text{M}}({text{z}}),,}

{displaystyle Delta Sigma {text{M}}({text{z}})={text{in}}({text{z}})cdot {text{z}}^{text{-1}}+{text{noise}}({text{z}})cdot (1-{text{z}}^{text{-1}}),.}

{displaystyle (1-{text{z}}^{text{-1}})}

primera diferencia hacia atrás

{displaystyle {text{z}}{=}1}

Moduladores de orden superior

Sin entrar en los detalles matemáticos,^{(ecuaciones 8 a 11)} cascada ${displaystyle Theta }$ integradores para crear un ${displaystyle Theta ^{text{th}}}$ -orden Modulador resultados en:

{displaystyle Delta Sigma {text{M}}_{Theta }({text{z}})={text{in}}({text{z}})cdot {text{z}}^{text{-1}}+{text{noise}}({text{z}})cdot (1-{text{z}}^{text{-1}})^{Theta },.}

primera diferencia hacia atrás

{displaystyle Theta }

Número teórico efectivo de bits

La relación teórica de señal a ruido (SNR) en decibeles (dB) por una entrada sinusoide que viaja a través de una ${displaystyle Theta ^{text{th}}}$ -orden modulador con un ${displaystyle 2^{d}}$ OSR (y seguido de un filtro ideal de decimación de baja pasada) puede ser matemáticamente derivado a ser aproximadamente:^{(ecuaciones 12 a 21)}

{displaystyle {text{SNR}}_{text{dB}}approx 3.01cdot (2cdot Theta +1)cdot d-9.36cdot Theta -2.76,.}

{textstyle Theta +{tfrac {1}{2}}}

{displaystyle d}

{textstyle d-{tfrac {3}{2}}}

{displaystyle {tfrac {1}{2}}}

1.3^st

SNR & ENOB contra la relación de oversampling (OSR) de la orden y el orden de la Δ ElisabethM
	Superficie de muestreo					cada una de ellas duplicación
	2⁴ OSR	2⁵ OSR	2⁶ OSR	2⁷ OSR	2⁸ OSR	cada una de ellas duplicación
1^st-orden:	24 dB 3+3.4 bits	33 dB 5+1.4 bits	42 dB 6+3.4 bits	51 dB 8+1.4 bits	60 dB 9+3.4 bits	+1+1.2 bits
2^nd-orden:	39 dB 6+1.4 bits	54 dB 8+3.4 bits	69 dB 11+1.4 bits	84 dB 13+3.4 bits	99 dB 16+1.4 bits	+2+1.2 bits
3^rd-orden:	53 dB 8+3.4 bits	75 dB 12+1.4 bits	96 dB 15+3.4 bits	117 dB 19+1.4 bits	138 dB 22+3.4 bits	+3+1.2 bits
4^T-orden:	68 dB 11+1.4 bits	95 dB 15+3.4 bits	112 dB 20+1.4 bits	149 dB 24+3.4 bits	177 dB 29+1.2 bits	+4+1.2 bits
5^T-orden:	83 dB 13+1.2 bits	116 dB 19 bits	149 dB 24+1.2 bits	182 dB 30 bits	215 dB 35+1.2 bits	+5+1.2 bits
6^T-orden:	99 dB 16 bits	137 dB 22+1.2 bits	176 dB 29 bits	215 dB 35+1.2 bits	254 dB 42 bits	+6+1.2 bits
cada pedido adicional:	+2+1.2 bits	+3+1.2 bits	+4+1.2 bits	+5+1.2 bits	+6+1.2 bits

Estos datos son teóricos. En la práctica, los circuitos experimentan inevitablemente otras fuentes de ruido que limitan la resolución, haciendo que las células de mayor resolución sean poco prácticas.

Relación con la modulación delta

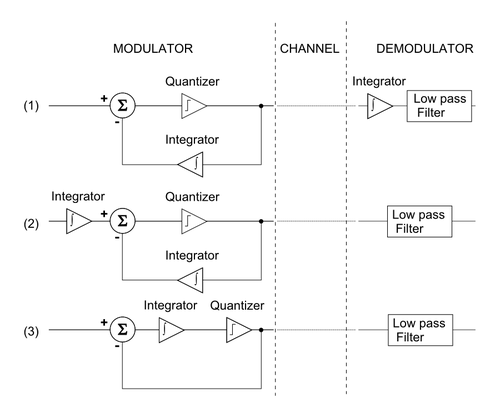
La modulación Delta-sigma está relacionada con la modulación del delta por los siguientes pasos (Figura 7):^§6

Comience con un diagrama de bloque de un modulador/demodulador delta.
La propiedad lineal de la integración, ${textstyle int a+int b=int (a+b)}$ , hace posible mover el integrador, que reconstruye la señal analógica en la sección de demodulador, frente al modulador delta.
Una vez más, la propiedad lineal de integración permite combinar a los dos integradores y obtener un diagrama de bloque de modulador/demodulador delta-sigma.

Si la cuantificación fuera homogénea (por ejemplo, si fuera lineal), lo anterior sería una derivación suficiente de su equivalencia hipotética. Pero debido a que el cuantificador no es homogéneo, delta-sigma está inspirado en la modulación delta, pero los dos tienen un funcionamiento distinto.

Desde el primer diagrama de bloques en la Figura 7, el integrador en la ruta de retroalimentación puede ser eliminado si la retroalimentación se toma directamente de la entrada del filtro de paso bajo. Por lo tanto, para la modulación delta de la señal de entrada $v dentro$ , el filtro de baja velocidad ve la señal

{displaystyle int operatorname {Quantize} left({text{v}}_{text{in}}-{text{v}}_{{text{feedback}}_{Delta }}right)dt.,}

Sin embargo, la modulación delta-sigma de los mismos lugares de señal de entrada en el filtro de paso bajo

{displaystyle operatorname {Quantize} left(int left({text{v}}_{text{in}}-{text{v}}_{{text{feedback}}_{Delta Sigma }}right)dtright).,}

En otras palabras, realizar modulación delta-sigma en lugar de modulación delta ha cambiado efectivamente el orden de las operaciones del integrador y del cuantificador. El efecto neto es una implementación más simple que tiene el profundo beneficio adicional de configurar el ruido de cuantificación para que esté principalmente en frecuencias por encima de las señales de interés. Este efecto se vuelve más dramático con un mayor sobremuestreo, lo que permite que el ruido de cuantificación sea algo programable. Por otro lado, la modulación delta da forma tanto al ruido como a la señal por igual.

Además, el cuantificador (por ejemplo, comparador) utilizado en la modulación delta tiene una pequeña salida que representa un pequeño paso hacia arriba y hacia abajo en la aproximación cuantificada de la entrada, mientras que el cuantificador utilizado en delta-sigma debe tomar valores fuera del rango de la señal de entrada.

En general, delta-sigma tiene algunas ventajas frente a la modulación delta:

La estructura se simplifica como
- sólo se necesita un integrador,
- el demodulador puede ser un simple filtro lineal (por ejemplo, filtro RC o LC) para reconstruir la señal, y
- el cuantificador (por ejemplo, la comparación) puede tener productos a gran escala.
El valor cuantificado es la parte integral de la señal de diferencia, que
- hace que sea menos sensible a la tasa de cambio de la señal, y
- ayuda a capturar componentes de baja frecuencia y DC.

Ejemplo de conversión de analógico a digital

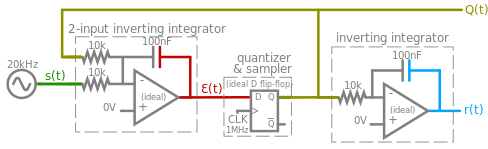
Figure 8a: Schematic of simple delta-sigma convertidor.

Figura 8b: Vista de alcance simulada de señales de tensión clave con el tiempo. Cada división vertical menor es de 1 μs, que corresponde a un evento de muestreo del reloj de 1 MHz.

Los ADC Delta-sigma varían en complejidad. El siguiente circuito se centra en un ADC delta-sigma síncrono de cuantificación de 2 niveles y primer orden simple sin diezmado.

Ejemplo de circuito simplificado

Para facilitar la comprensión, se simula un esquema de circuito simple (Figura 8a) que utiliza elementos ideales (voltajes de Figura 8b). Funcionalmente el mismo bucle de modulación ΔΣ analógico a digital de la Figura 1 (nota: el integrador inversor de 2 entradas combina la unión sumadora y el integrador y produce un resultado de retroalimentación negativa, y el flip-flop combina el cuantificador muestreado y, de forma conveniente y natural). también funciona como un DAC de 1 bit).

La onda sinusoidal de entrada de 20 kHz s(t) se convierte en un resultado digital PDM de 1 bit Q(t). Se utiliza 20 kHz como ejemplo porque se considera el límite superior de la audición humana.

Este circuito se puede diseñar en una placa con componentes discretos económicos (tenga en cuenta que algunas variaciones usan polarización diferente y filtros de paso bajo RC más simples para la integración en lugar de amplificadores operacionales).

Para simplificar, el flip-flop D se alimenta con voltajes de suministro duales de V_DD = +1 V y V_SS = -1 V, por lo que su salida binaria Q(t) es +1 V o -1 V.

Integrador inversor de 2 entradas

El integrador de amplificador operacional inversor de 2 entradas combina s(t) con Q(t) para producir Ɛ(t):

{displaystyle varepsilon (t)=-{frac {1}{RC}}int (s(t)+Q(t))dt.}

Ɛ(t)s(t)Q(t)Ɛ(t)milivolts

Debido al signo negativo del integrador, cuando Ɛ(t) luego se muestrea para producir Q(t), el +Q(t) en esta integral en realidad representa retroalimentación negativa del ciclo de reloj anterior.

Flip-flop de cuantizador y sampler

Un flip-flop D ideal muestra Ɛ(t) a una frecuencia de reloj de 1 MHz. La vista de alcance (Figura 6b) tiene una división menor igual al período de muestreo de 1 μs, por lo que cada división menor corresponde a un evento de muestreo. Dado que se supone que el flip-flop es ideal, trata cualquier voltaje de entrada mayor que 0 V como lógico alto y cualquier voltaje de entrada menor que 0 V como lógico bajo, sin importar qué tan cerca esté de 0 V (ignorando cuestiones de muestreo). violaciones del tiempo de retención y metaestabilidad).

Siempre que ocurre un evento de muestreo:

si Ɛ(t) está por encima del umbral de 0 V, entonces Q(t) (+1 V), o
si Ɛ(t) está debajo del umbral de 0 V, entonces Q(t) bajará (-1 V).

Q(t) se envía como la salida PDM resultante y también se alimenta al integrador de 2 entradas.

Demodulación

El integrador situado más a la derecha realiza la conversión de digital a analógico en Q(t) para producir una salida analógica demodulada r(t), que reconstruye la entrada de la onda sinusoidal original como segmentos diagonales lineales por partes. Aunque r(t) parece tosco con esta tasa de sobremuestreo de 50x, r(t) se puede filtrar de paso bajo para aislar la señal original. A medida que aumenta la frecuencia de muestreo en relación con la frecuencia máxima de la señal de entrada, r(t) se aproximará más a la entrada original s(t).

Conversión de digital a analógico

Vale la pena señalar que, si nunca se produjo ninguna destrucción, la representación digital de un modulador delta-sigma de 1 bit es simplemente una señal PDM, que se puede convertir fácilmente a analógica usando un filtro de paso bajo, tan simple como una resistencia y un condensador.

Sin embargo, en general, un DAC delta-sigma convierte una señal de serie temporal discreta de muestras digitales con una profundidad de bits alta en una señal de profundidad de bits baja (a menudo 1 bit), generalmente a una frecuencia de muestreo mucho más alta. Esa señal modulada en delta luego se puede convertir con precisión en analógica (ya que los DAC de menor profundidad de bits son más fáciles de ser altamente lineales), que luego pasa por un filtrado de paso bajo económico en el dominio analógico para eliminar el ruido de cuantificación de alta frecuencia inherente a la señal. Proceso de modulación delta-sigma.

Levantamiento

Como explican los artículos sobre la transformada de Fourier discreta y la transformada de Fourier de tiempo discreto, una señal muestreada periódicamente contiene inherentemente múltiples copias o "imágenes" de la señal. A menudo es deseable eliminar estas imágenes de mayor frecuencia antes de realizar la etapa de modulación delta-sigma real, para aliviar los requisitos del eventual filtro analógico de paso bajo. Esto se puede hacer mediante un muestreo superior utilizando un filtro de interpolación y, a menudo, es el primer paso antes de realizar la modulación delta-sigma en los DAC. El muestreo ascendente está fuertemente asociado con los DAC delta-sigma, pero no es estrictamente parte de la etapa de modulación delta-sigma real (similar a cómo la diezmación está fuertemente asociada con los ADC delta-sigma, pero tampoco es estrictamente parte de la modulación delta-sigma), y los detalles son fuera del alcance de este artículo.

Modulación delta-sigma de digital a digital

El bucle de modulación de la Figura 6 en § Modelado de ruido se puede diseñar fácilmente con elementos digitales básicos de un restador para la diferencia, un acumulador para el integrador y un registro de bits más bajos para la cuantificación, que transfiere la mayor parte -bit(s) significativo(s) del integrador para ser la retroalimentación para el siguiente ciclo.

Conformación de ruido en varias etapas

Esta sencilla modulación de primer orden se puede mejorar conectando en cascada dos o más acumuladores desbordantes, cada uno de los cuales equivale a un modulador delta-sigma de primer orden. . La estructura de conformación de ruido de múltiples etapas (MASH) resultante tiene una propiedad de conformación de ruido más pronunciada, por lo que se usa comúnmente en audio digital. Las salidas de acarreo se combinan mediante sumas y retrasos para producir una salida binaria, cuyo ancho depende del número de etapas (orden) del MASH. Además de su función de modelado de ruido, tiene dos propiedades más atractivas:

simple de implementar en hardware; sólo se requieren bloques digitales comunes como acumuladores, adidores y volteretas D
incondicionalmente estable (no hay bucles de retroalimentación fuera de los acumuladores)

Naming

La técnica fue presentada por primera vez a principios de la década de 1960 por el profesor Yasuhiko Yasuda mientras estudiaba en la Universidad de Tokio. El nombre delta-sigma proviene directamente de la presencia de un modulador delta y un integrador, como lo introdujeron por primera vez Inose et al. en su solicitud de patente. Es decir, el nombre proviene de integrar o suma diferencias, que, en matemáticas, son operaciones habitualmente asociadas a las letras griegas sigma y delta respectivamente.

En la década de 1970, los ingenieros de Bell Labs utilizaban los términos "sigma-delta" porque el precedente fue nombrar variaciones de la modulación delta con adjetivos precediendo a "delta", y un editor de la revista Analog Devices justificó en 1990 que la jerarquía funcional es "sigma-delta", porque calcula la integral de una diferencia.

Ambos nombres sigma-delta y delta-sigma se utilizan con frecuencia.

Modulación asíncrona delta-sigma

Kirkkert y Miller publicaron una variante de tiempo continuo llamada "Modulación Delta Sigma asíncrona" en 1975. En lugar de utilizar un comparador para la cuantificación como se hace en la modulación ΔΣ síncrona, la modulación ΔΣ asíncrona (ADSM o ASDM) utiliza un disparador Schmitt (es decir, un comparador con histéresis) o (como sostiene el artículo es equivalente) un comparador con retraso fijo.

En el ejemplo de la Figura 9, cuando la integral del error excede sus límites, la salida cambia de estado, produciendo una onda de salida modulada por ancho de pulso (PWM).

Contenido relacionado

Más resultados...