Modelo mixto

Un modelo mixto, modelo de efectos mixtos o modelo de componentes de error mixto es un modelo estadístico que contiene tanto efectos fijos como efectos aleatorios. Estos modelos son útiles en una amplia variedad de disciplinas de las ciencias físicas, biológicas y sociales. Son particularmente útiles en entornos en los que se realizan mediciones repetidas en las mismas unidades estadísticas (véase también estudio longitudinal), o cuando las mediciones se realizan en grupos de unidades estadísticas relacionadas. Los modelos mixtos suelen preferirse a los modelos de regresión de análisis de varianza tradicionales porque no se basan en el supuesto de observaciones independientes. Además, tienen su flexibilidad para tratar los valores faltantes y el espaciado desigual de las mediciones repetidas. El análisis del modelo mixto permite que las mediciones se modelen explícitamente en una variedad más amplia de estructuras de correlación y varianza-covarianza, evitando estimaciones sesgadas.

En esta página se analizarán principalmente los modelos lineales de efectos mixtos, en lugar de los modelos lineales mixtos generalizados o los modelos no lineales de efectos mixtos.

Los modelos lineales mixtos (LMM) son modelos estadísticos que incorporan efectos fijos y aleatorios para representar con precisión estructuras de datos no independientes. Los LMM son una alternativa al análisis de varianza. A menudo, el ANOVA supone la independencia de las observaciones dentro de cada grupo; sin embargo, esta suposición puede no ser válida en datos no independientes, como conjuntos de datos multinivel/jerárquicos, longitudinales o correlacionados.

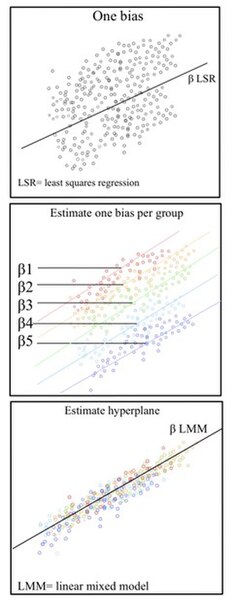
Los conjuntos no independientes son aquellos en los que la variabilidad entre los resultados se debe a correlaciones dentro de los grupos o entre grupos. Los modelos mixtos dan cuenta adecuadamente de las estructuras de datos anidadas/jerárquicas en las que las observaciones se ven influidas por sus asociaciones anidadas. Por ejemplo, al estudiar métodos educativos que involucran a varias escuelas, hay varios niveles de variables a considerar. El nivel individual/nivel inferior comprende estudiantes o profesores individuales dentro de la escuela. Las observaciones obtenidas de este estudiante/profesor están anidadas dentro de su escuela. Por ejemplo, el Estudiante A es una unidad dentro de la Escuela A. El siguiente nivel superior es la escuela. En el nivel superior, la escuela contiene varios estudiantes y profesores individuales. El nivel de la escuela influye en las observaciones obtenidas de los estudiantes y profesores. Por ejemplo, la Escuela A y la Escuela B son los niveles superiores, cada uno con su conjunto de Estudiante A y Estudiante B respectivamente. Esto representa un esquema de datos jerárquico. Una solución para modelar datos jerárquicos es utilizar modelos mixtos lineales.

Los LMM nos permiten comprender los efectos importantes entre niveles y dentro de ellos, al tiempo que incorporan las correcciones de los errores estándar por falta de independencia incorporadas en la estructura de datos.

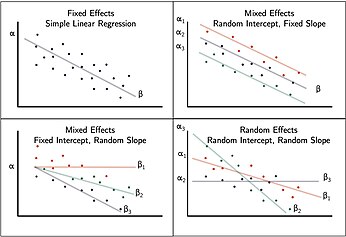
Los efectos fijos encapsulan las tendencias que son consistentes en los niveles de interés primario. Estos efectos se consideran fijos porque no son aleatorios y se supone que son constantes para la población en estudio. Por ejemplo, al estudiar la educación, un efecto fijo podría representar efectos generales a nivel escolar que sean consistentes en todas las escuelas.

Si bien la jerarquía del conjunto de datos suele ser obvia, se deben especificar los efectos fijos específicos que afectan las respuestas promedio de todos los sujetos. Algunos coeficientes de efectos fijos son suficientes sin los efectos aleatorios correspondientes, mientras que otros coeficientes fijos solo representan un promedio en el que las unidades individuales son aleatorias. Estos se pueden determinar incorporando interceptos y pendientes aleatorios.

En la mayoría de las situaciones se consideran varios modelos relacionados y se adopta el modelo que mejor representa un modelo universal.

Un componente clave del modelo mixto es la incorporación de efectos aleatorios con el efecto fijo. Los efectos fijos se ajustan a menudo para representar el modelo subyacente. En los modelos mixtos lineales, la verdadera regresión de la población es lineal, β. Los datos fijos se ajustan en el nivel más alto. Los efectos aleatorios introducen variabilidad estadística en diferentes niveles de la jerarquía de datos. Estos dan cuenta de las fuentes de varianza no medidas que afectan a ciertos grupos en los datos. Por ejemplo, las diferencias entre el estudiante 1 y el estudiante 2 en la misma clase, o las diferencias entre la clase 1 y la clase 2 en la misma escuela.

Ronald Fisher introdujo los modelos de efectos aleatorios para estudiar las correlaciones de los valores de los rasgos entre parientes. En la década de 1950, Charles Roy Henderson proporcionó las mejores estimaciones lineales imparciales de los efectos fijos y las mejores predicciones lineales imparciales de los efectos aleatorios. Posteriormente, el modelado mixto se ha convertido en un área importante de la investigación estadística, que incluye el trabajo sobre el cálculo de estimaciones de máxima verosimilitud, modelos de efectos mixtos no lineales, datos faltantes en modelos de efectos mixtos y estimación bayesiana de modelos de efectos mixtos. Los modelos mixtos se aplican en muchas disciplinas en las que se realizan múltiples mediciones correlacionadas en cada unidad de interés. Se utilizan de forma destacada en la investigación que involucra sujetos humanos y animales en campos que van desde la genética hasta el marketing, y también se han utilizado en el béisbol y las estadísticas industriales. La asociación del modelo lineal mixto ha mejorado la prevención de asociaciones de falsos positivos. Las poblaciones están profundamente interconectadas y la estructura de parentesco de la dinámica de la población es extremadamente difícil de modelar sin el uso de modelos mixtos. Sin embargo, los modelos lineales mixtos pueden no ser la única solución. Los modelos LMM tienen un supuesto de varianza residual constante que a veces se viola cuando se contabilizan características continuas y binarias profundamente asociadas.

En notación matricial, un modelo lineal mixto se puede representar como

${\displaystyle {\beta}=X{\boldsymbol {\beta} #Z{\boldsymbol {u}+{\boldsymbol {\epsilon}}$

donde

• ${\displaystyle {\bu}}}$ es un vector conocido de observaciones, con media ${\displaystyle E({\boldsymbol {y}})=X{\boldsymbol {\beta }$;
• ${\displaystyle {\boldsymbol {\beta }$ es un vector desconocido de efectos fijos;
• ${\displaystyle {\bu}}$ es un vector desconocido de efectos aleatorios, con media ${\displaystyle E({\boldsymbol {u}})={\boldsymbol {0}}$ y matriz de variabilidad y covariancia ${\displaystyle \operatorname {var} ({\boldsymbol {u}}=G}$;
• ${\displaystyle {\boldsymbol {\epsilon}}$ es un vector desconocido de errores aleatorios, con media ${\displaystyle E({\boldsymbol {\epsilon }}={\boldsymbol {0}}$ y diferencia ${\displaystyle \operatorname {var} ({\boldsymbol {\epsilon })=R}$;
• ${\displaystyle X}$ es la matriz de diseño conocida para los efectos fijos relacionados con las observaciones ${\displaystyle {\bu}}}$ a ${\displaystyle {\boldsymbol {\beta }$, respectivamente
• ${\displaystyle Z}$ es la matriz de diseño conocida para los efectos aleatorios relacionados con las observaciones ${\displaystyle {\bu}}}$ a ${\displaystyle {\bu}}$, respectivamente.

Por ejemplo, si cada observación puede pertenecer a cero o más de k categorías, entonces Z, que tiene una fila por observación, se puede elegir para que tenga k columnas, donde un valor de 1 para un elemento de matriz de Z indica que se sabe que una observación pertenece a una categoría y un valor de 0 indica que se sabe que una observación no pertenece a una categoría. El valor inferido de u para una categoría es entonces una intersección específica de la categoría. Si Z tiene columnas adicionales, donde los valores distintos de cero son en cambio el valor de una variable independiente para una observación, entonces el valor inferido correspondiente de u es una pendiente específica de la categoría para esa variable independiente. La distribución previa para las intersecciones y pendientes de la categoría se describe mediante la matriz de covarianza G.

La densidad de articulación ${\displaystyle {\bu}}}$ y ${\displaystyle {\bu}}$ puede ser escrito como: ${\\fnMicrosoft Sans Serif} {\\fnMicrosoft Sans Serif} {\f}}} {\boldsymbol {\f}}}} {\boldsymbol {u})\,f({\boldsymbol {u}}}}}}}}$. Suponiendo normalidad, ${\displaystyle {\boldsymbol {u}}\sim {\mathcal {N}({\boldsym {0}},G)}$, ${\displaystyle {\boldsymbol {\epsilon}\sim {\mathcal {N}({\boldsymbol {0}}R)}$ y ${\displaystyle \mathrm {} {\boldsymbol {u}},{\boldsymbol {\epsilon }}}={\boldsymbol {0}}$, y maximizar la densidad de articulación sobre ${\displaystyle {\boldsymbol {\beta }$ y ${\displaystyle {\bu}}$, da Henderson "ecuaciones de modelos mezclados" (MME) para modelos mixtos lineales:

${\displaystyle {\begin{pmatrix}X'R^{-1}X 'R^{-1}Z\\Z'R^{-1}X limitZ'R^{-1}Z+G^{-1}\end{pmatrix}{\begin{pmatrix}{\hattrix}{\hattrix} {\beta} ### {\fncip {\fnK}}\end{pmatrix}={\begin{pmatrix}X'R^{-1}{\boldsymbol {y}\\\\\\fnK} {\fnK}} {\fnK}}} {\fn}}} {\fn}}}}}}}$

donde, por ejemplo, X′ es la matriz transpuesta de X y R⁻¹ es la matriz inversa de R.

Las soluciones al MME, ${\displaystyle \textstyle {\hat {\beta }$ y ${\displaystyle \textstyle {\hat {\bu}}}$ son las mejores estimaciones y predictores lineales sin prejuicios ${\displaystyle {\boldsymbol {\beta }$ y ${\displaystyle {\bu}}$, respectivamente. Esta es una consecuencia del teorema Gauss–Markov cuando la variabilidad condicional del resultado no es escalable a la matriz de identidad. Cuando se conoce la varianza condicional, entonces la varianza inversa ponderada estimación de los mínimos cuadrados es la mejor estimación lineal imparcial. Sin embargo, la varianza condicional es rara vez, si alguna vez, conocida. Por lo tanto, es conveniente estimar conjuntamente las estimaciones de variabilidad y parámetro ponderado al resolver MMEs.

Un método utilizado para ajustar estos modelos mixtos es el algoritmo de expectativa-maximización (EM), en el que los componentes de la varianza se tratan como parámetros de molestia no observados en la probabilidad conjunta. Actualmente, este es el método implementado en software estadístico como Python (paquete statsmodels) y SAS (proc mixed), y como paso inicial solo en el paquete nlme lme() de R. La solución a las ecuaciones del modelo mixto es una estimación de máxima verosimilitud cuando la distribución de los errores es normal.

Hay varios otros métodos para adaptarse a los modelos mixtos, incluyendo el uso de un MEM inicialmente, y luego Newton-Raphson (utilizado por R package lme()), penalizó los mínimos cuadrados para obtener una probabilidad de registro perfilado sólo dependiendo de los parámetros de varianza-covariancia (low-dimensional) ${\displaystyle {\bu}}$, es decir, su matriz cov ${\displaystyle {\boldsymbol {G}}$, y luego la optimización directa moderna para esa función objetiva reducida (utilizada por el paquete lme4 lmer() de R y el paquete Julia MixedModels.jl) y la optimización directa de la probabilidad (utilizada por e.g. R's glmmTMB). Notablemente, aunque la forma canónica propuesta por Henderson es útil para la teoría, muchos paquetes de software populares utilizan una formulación diferente para la computación numérica con el fin de aprovechar los métodos de matriz escasa (por ejemplo lme4 y MixedModels.jl).

• Modelo de efectos mixtos no lineales
• Modelo de efectos fijos
• Modelo mixto lineal generalizado
• Regreso lineal
• Análisis de la varianza de diseño mixto
• Modelo multinivel
• Modelo de efectos aleatorios
• Diseño de medidas repetidas
• Método empírico Bayes

• Gałecki, Andrzej; Burzykowski, Tomasz (2013). Modelos de Efectos mixtos lineales utilizando R: A Step-by-Step Approach. Nueva York: Springer. ISBN 978-1-4614-3900-4.
• Milliken, G. A.; Johnson, D. E. (1992). Análisis de Messy Datos: Vol. I. Experimentos diseñados. New York: Chapman & Hall.
• West, B. T.; Welch, K. B.; Galecki, A. T. (2007). Mezcla lineal Modelos: Una guía práctica que utiliza el software estadístico. Nueva York: Chapman " Hall/CRC.