Modelo de semiplano de Poincaré

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Modelo plano de la geometría hiperbólica no euclidiana

En la geometría no euclidiana, la Poincaré half-plane model es el medio plano superior, denotado abajo como H $0;x,yin mathbb {R} }}" xmlns="http://www.w3.org/1998/Math/MathML">={}.. x,Sí... ▪ ▪ Sí.■0;x,Sí.▪ ▪ R}{displaystyle ={langle x,yrangle mid y título0;x,yin mathbb {R}}0;x,yin mathbb {R} }}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/da400e1856ed556278b83c85cf68151302aaebeb" style="vertical-align: -0.838ex; width:26.532ex; height:2.843ex;"/>$ , junto con una métrica, la métrica Poincaré, que lo convierte en un modelo de geometría hiperbólica bidimensional.

De manera equivalente, el modelo de semiplano de Poincaré a veces se describe como un plano complejo donde la parte imaginaria (la coordenada y mencionada anteriormente) es positiva.

El modelo de semiplano de Poincaré lleva el nombre de Henri Poincaré, pero se originó con Eugenio Beltrami, quien lo utilizó, junto con el modelo de Klein y el modelo de disco de Poincaré, para demostrar que la geometría hiperbólica era equiconsistente con la geometría euclidiana.

Este modelo es conforme, lo que significa que los ángulos medidos en un punto son los mismos en el modelo que en el plano hiperbólico real.

La transformada de Cayley proporciona una isometría entre el modelo de semiplano y el modelo de disco de Poincaré.

Este modelo se puede generalizar para modelar $n+1$ espacio hiperbólico dimensional reemplazando el número real x por un vector en un n Espacio vectorial dimensional Euclidean.

Métrica

La métrica del modelo en el medio plano, $0},}" xmlns="http://www.w3.org/1998/Math/MathML">{}.. x,Sí... ▪ ▪ Sí.■0},{displaystyle {langle x,yrangle mid y título0},}0},}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/78c28080edaa9eb0ff348bcee0393a5ed2e6954f" style="vertical-align: -0.838ex; width:15.654ex; height:2.843ex;"/>$ es:

{displaystyle (ds)^{2}={frac {(dx)^{2}+(dy)^{2}}{y^{2}}}}

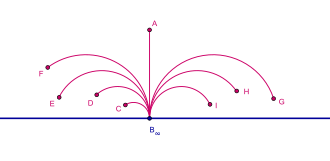
donde s mide la longitud a lo largo de una línea (posiblemente curva). Las líneas rectas en el plano hiperbólico (geodésicas para este tensor métrico, es decir, curvas que minimizan la distancia) se representan en este modelo mediante arcos circulares perpendiculares al eje x. (semicírculos cuyos centros están en el eje x) y rayos verticales rectos perpendiculares al eje x.

Cálculo de distancia

Si ${textstyle p_{1}=langle x_{1},y_{1}rangle }$ y ${textstyle p_{2}=langle x_{2},y_{2}rangle }$ son dos puntos en el medio plano $0}" xmlns="http://www.w3.org/1998/Math/MathML">Sí.■0{textstyle y confía0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/bad11e7747271c5d6ebd668b512129802597fc5c" style="vertical-align: -0.671ex; width:5.416ex; height:2.509ex;"/>$ y ${textstyle {tilde {p}}_{1}=langle x_{1},-y_{1}rangle }$ es el reflejo de ${textstyle p_{1}}$ a través de x-eje en el medio plano inferior, el distancia entre los dos puntos bajo la métrica del plan hiperbólico es:

{displaystyle {begin{aligned}operatorname {dist} (p_{1},p_{2})&=2operatorname {arsinh} {frac {|p_{2}-p_{1}|}{2{sqrt {y_{1}y_{2}}}}}\[10mu]&=2operatorname {artanh} {frac {|p_{2}-p_{1}|}{|p_{2}-{tilde {p}}_{1}|}}\[10mu]&=2ln {frac {|p_{2}-p_{1}|+|p_{2}-{tilde {p}}_{1}|}{2{sqrt {y_{1}y_{2}}}}},end{aligned}}}

Donde ${textstyle |p_{2}-p_{1}|={sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}}$ es la distancia euroclidiana entre puntos ${textstyle p_{1}}$ y ${textstyle p_{2},}$ ${textstyle operatorname {arsinh} x=ln {bigl (}x+{sqrt {x^{2}+1}}{bigr)}}$ es el seno hiperbólico inverso, y ${textstyle operatorname {artanh} x={frac {1}{2}}ln left((1+x)/(1-x)right)}$ es el tangente hiperbólico inverso. Esto ${textstyle 2operatorname {arsinh} }$ fórmula se puede pensar que viene de la longitud del acorde en la métrica Minkowski entre puntos en el modelo hiperboloide, ${textstyle operatorname {chord} (p_{1},p_{2})=2sinh {tfrac {1}{2}}operatorname {dist} (p_{1},p_{2}),}$ análogo a encontrar la arclength en una esfera en términos de longitud de acorde. Esto ${textstyle 2operatorname {artanh} }$ se puede pensar que la fórmula proviene de la distancia euclidiana en el modelo de disco Poincaré con un punto en el origen, análoga a la búsqueda de la arclength en la esfera tomando una proyección estereográfica centrada en un punto y midiendo la distancia euclidiana en el plano desde el origen hasta el otro punto.

Si los dos puntos ${textstyle p_{1}}$ y ${textstyle p_{2}}$ están en una línea hiperbólica (Euclidean half-circle) que interseca x-eje en los puntos ideales ${textstyle p_{0}=langle x_{0},0rangle }$ y ${textstyle p_{3}=langle x_{3},0rangle}$ la distancia desde ${textstyle p_{1}}$ a ${textstyle p_{2}}$ es:

{displaystyle operatorname {dist} (p_{1},p_{2})=left|ln {frac {|p_{2}-p_{0}||p_{1}-p_{3}|}{|p_{1}-p_{0}||p_{2}-p_{3}|}}right|.}

Cfr. Proporción cruzada.

Algunos casos especiales pueden simplificarse. Dos puntos con el mismo ${textstyle x}$ coord:

{displaystyle operatorname {dist} (langle x,y_{1}ranglelangle x,y_{2}rangle)=left|ln {frac {y_{2}}{y_{1}}}right|=left|ln(y_{2})-ln(y_{1})right|.}

Dos puntos con el mismo ${textstyle y}$ coord:

{displaystyle operatorname {dist} left(langle x_{1},yranglelangle x_{2},yrangle right)=2operatorname {arsinh} {frac {|x_{2}-x_{1}|}{2y}}.}

Un punto ${textstyle langle x_{1},rrangle }$ en el ápice del semicírculo ${textstyle (x-x_{1})^{2}+y^{2}=r^{2},}$ y otro punto en un ángulo central ${textstyle phi.}$

{displaystyle operatorname {dist} (langle x_{1},rranglelangle x_{1}pm rsin phircos phi rangle)={2operatorname {artanh} }{bigl (}{tan {tfrac {1}{2}}phi }{bigr)}=operatorname {gd} ^{-1}phi}

Donde ${textstyle operatorname {gd} ^{-1}}$ es la función Gudermanniana inversa, y ${textstyle operatorname {artanh} x={tfrac {1}{2}}ln {dfrac {1+x}{1-x}}}$ es el tangente hiperbólico inverso.

Puntos y curvas especiales

Puntos ideales (puntos al infinito) en el modelo de medio plano Poincaré son de dos tipos:

los puntos sobre x-Eje, y
un punto imaginario $y=infty$ que es el punto ideal al que todas las líneas ortogonales a x- Eje converge.

Líneas rectas, geodésica (el camino más corto entre los puntos contenidos dentro de él) son modelados por cualquiera:

medio círculos cuyo origen está en el eje x
los rayos verticales rectos ortogonales al eje x

A círculo (curves equidistant desde un punto central) con centro $(x,y)$ y radio $r$ es modelado por:

un círculo con centro

(x,ycosh(r))

y radio

ysinh(r)

A hiperciclo (una curva equidistante de una línea recta, su eje) es modelado por cualquiera:

un arco circular que interseca x-eje en los mismos dos puntos ideales que el medio círculo que modela su eje pero en un ángulo agudo o obtuso
una línea recta que interseca x-eje en el mismo punto que la línea vertical que modela su eje, pero en un ángulo agudo o obtuso.

A horociclo (una curva cuyas normales convergen asintomáticamente en la misma dirección, su centro) es modelada por cualquiera:

un círculo tangente al x-eje (pero excluyendo el punto ideal de intersección, que es su centro)
una línea paralela a la x-eje, en este caso el centro es el punto ideal $y=infty$ .

Sinopsis euclidiana

Un círculo euclidiano con centro ${displaystyle langle x_{e},y_{e}rangle }$ y radio ${displaystyle r_{e}}$ representa:

cuando el círculo está completamente dentro del medioplano un círculo hiperbólico con centro

{displaystyle left(x_{e},{sqrt {y_{e}^{2}-r_{e}^{2}}}right)}

y radio

{displaystyle {frac {1}{2}}ln left({frac {y_{e}+r_{e}}{y_{e}-r_{e}}}right).}

cuando el círculo está completamente dentro del medio plano y toca el límite un horociclo centrado alrededor del punto ideal ${displaystyle (x_{e},0)}$
cuando el círculo intersecte el límite ortogonal ${displaystyle (y_{e}=0)}$ una línea hiperbólica
cuando el círculo intersecte el límite no ortogonal un hiperciclo.

Construcciones con compás y regla

A continuación se explica cómo se pueden utilizar construcciones con compás y regla en el modelo para lograr el efecto de las construcciones básicas en el plano hiperbólico. Por ejemplo, cómo construir el semicírculo en el semiplano euclidiano que modela una línea en el plano hiperbólico que pasa por dos puntos dados.

Creando la línea a través de dos puntos existentes

Dibuja el segmento de línea entre los dos puntos. Construye la mediatriz del segmento de recta. Encuentre su intersección con el eje x. Dibuja el círculo alrededor de la intersección que pasa por los puntos dados. Borre la parte que está en o debajo del eje x.

O en el caso especial donde los dos puntos dados se encuentran en una línea vertical, dibuje esa línea vertical a través de los dos puntos y borre la parte que está en o debajo del eje x.

Creando el círculo a través de un punto con centro en otro punto

Si los dos puntos no están en línea vertical:

Dibuja la línea radial (semicírculo) entre los dos puntos dados como en el caso anterior. Construye una tangente a esa línea en el punto no central. Coloque una perpendicular desde el punto central dado al eje x. Encuentra la intersección de estas dos líneas para obtener el centro del círculo modelo. Dibuja el círculo modelo alrededor de ese nuevo centro y pasando por el punto no central dado.

Si los dos puntos dados se encuentran en una línea vertical y el centro dado está por encima del otro punto dado:

Dibuje un círculo alrededor de la intersección de la línea vertical y el eje x que pasa por el punto central dado. Dibuja una línea horizontal a través del punto no central. Construye la tangente al círculo en su intersección con esa línea horizontal.

El punto medio entre la intersección de la tangente con la línea vertical y el punto no central dado es el centro del círculo modelo. Dibuja el círculo modelo alrededor de ese nuevo centro y pasando por el punto no central dado.

Si los dos puntos dados se encuentran en una línea vertical y el centro dado está por debajo del otro punto dado:

Dibuje un círculo alrededor de la intersección de la línea vertical y el eje x que pasa por el punto central dado. Traza una recta tangente a la circunferencia que pasa por el punto no central dado. Dibuja una línea horizontal que pase por ese punto de tangencia y encuentra su intersección con la línea vertical.

El punto medio entre esa intersección y el punto no central dado es el centro del círculo modelo. Dibuja el círculo modelo alrededor de ese nuevo centro y pasando por el punto no central dado.

Dado un círculo, encuentre su centro (hiperbólico)

Coloca una p perpendicular desde el centro euclidiano del círculo hasta el eje x.

Sea el punto q la intersección de esta línea y el eje x.

Dibuja una línea tangente al círculo que pasa por q.

Dibuja el semicírculo h con centro q pasando por el punto donde se unen la tangente y el círculo.

Did you mean:

The (hyperbolic) center is the point where h and p intersection.

Otras construcciones

Crear el punto que es la intersección de dos líneas existentes, si se intersectan:

Encuentra la intersección de los dos semicírculos dados (o líneas verticales).

Creando uno o dos puntos en la intersección de una línea y un círculo (si se intersectan):

Encuentra la intersección del semicírculo dado (o línea vertical) con el círculo dado.

Creando uno o dos puntos en la intersección de dos círculos (si se intersectan):

Encuentra la intersección de los dos círculos dados.

Grupos de simetría

El grupo lineal proyectivo PGL(2,C) actúa sobre la esfera de Riemann mediante las transformaciones de Möbius. El subgrupo que mapea el semiplano superior, H, sobre sí mismo es PSL(2,R), las transformadas con coeficientes reales, y éstas actúan transitiva e isométricamente sobre el semiplano superior, convirtiéndolo en un espacio homogéneo.

Hay cuatro grupos de Lie estrechamente relacionados que actúan en el semiplano superior mediante transformaciones lineales fraccionarias y preservan la distancia hiperbólica.

El grupo lineal especial SL(2,R) que consiste en el conjunto de matrices 2×2 con entradas reales cuyo determinante equivale a +1. Note que muchos textos (incluyendo Wikipedia) a menudo dicen SL(2,RCuando realmente quieren decir PSL(2,R).
El grupo S*L(2,R) que consiste en el conjunto de matrices 2×2 con entradas reales cuyo determinante equivale a +1 o −1. Note que SL(2,R) es un subgrupo de este grupo.
Grupo lineal especial de proyecto PSL(2,R) = SL(2,R)/{I}, que consiste en las matrices en SL(2,R) modulo más o menos la matriz de identidad.
El grupo PS^*L(2,R) = S^*L(2,R)/{I}=PGL(2,R) es de nuevo un grupo proyector, y de nuevo, modulo más o menos la matriz de identidad. PSL(2,R) se contiene como un subgrupo índice-dos normal, el otro conjunto es el conjunto de matrices 2×2 con entradas reales cuyo determinante equivale a −1, modulo más o menos la identidad.

La relación de estos grupos con el modelo de Poincaré es la siguiente:

El grupo de todas las isometrías H, a veces denotado como Isom(H), es isomorfo para PS^*L(2,R). Esto incluye tanto la preservación de la orientación como las isometrías de inversión de orientación. El mapa de inversión de orientación (el mapa del espejo) es $zrightarrow -{overline {z}}$ .
The group of orientation-preserving isometries of H, a veces denotado como⁺()H), es isomorfo a PSL(2,R).

Los subgrupos importantes del grupo de isometría son los grupos fucsianos.

También se ve frecuentemente el grupo modular SL(2,Z). Este grupo es importante en dos sentidos. Primero, es un grupo de simetría de la red de puntos cuadrada de 2x2. Por lo tanto, las funciones que son periódicas en una cuadrícula, como las formas modulares y las funciones elípticas, heredarán una simetría SL(2,Z) de la cuadrícula. En segundo lugar, SL(2,Z) es, por supuesto, un subgrupo de SL(2,R) y, por lo tanto, tiene un comportamiento hiperbólico incorporado. En particular, SL(2,Z) se puede utilizar para teselar el plano hiperbólico en celdas de igual área (Poincaré).

Simetría isométrica

La acción grupal del grupo lineal especial proyectivo ${displaystyle {rm {PSL}}(2,mathbb {R})}$ on $mathbb {H}$ se define por

${displaystyle {begin{pmatrix}a&b\c&d\end{pmatrix}}cdot z={frac {az+b}{cz+d}}={frac {(ac|z|^{2}+bd+(ad+bc)Re (z))+i(ad-bc)Im (z)}{|cz+d|^{2}}}.}$

Tenga en cuenta que la acción es transitiva: para cualquier $z_{1},z_{2}in mathbb {H}$ , existe un ${displaystyle gin {rm {PSL}}(2,mathbb {R})}$ tales que $gz_{1}=z_{2}$ . Es también fiel, en eso si $gz=z$ para todos ${displaystyle zin mathbb {H}}$ entonces g = e.

El estabilizador o subgrupo de isotropía de un elemento ${displaystyle zin mathbb {H} }$ es el conjunto de ${displaystyle gin {rm {PSL}}(2,mathbb {R})}$ licencia z sin cambios: gz = z. El estabilizador de i es el grupo de rotación

${displaystyle {rm {SO}}(2)=left.left{{begin{pmatrix}cos theta &sin theta \-sin theta &cos theta \end{pmatrix}}right|theta in mathbb {R} right}.}$

Desde cualquier elemento ${displaystyle zin mathbb {H} }$ es mapeado a i por algún elemento ${displaystyle {rm {PSL}}(2,mathbb {R})}$ , esto significa que el subgrupo isotropía de cualquier z es isomorfo a SO(2). Así, ${displaystyle mathbb {H} ={rm {PSL}}(2,mathbb {R})/{rm {SO}}(2)}$ . Alternativamente, el paquete de vectores tangentes de longitud unitaria en el medio plano superior, llamado el paquete tangente unidad, es isomorfo a ${displaystyle {rm {PSL}}(2,mathbb {R})}$ .

El medio plano superior está tesellado en conjuntos regulares libres por el grupo modular ${displaystyle {rm {SL}}(2,mathbb {Z}).}$

Geodésicas

Las geodésicas para este tensor métrico son arcos circulares perpendiculares al eje real (semicírculos cuyo origen está en el eje real) y líneas rectas verticales que terminan en el eje real.

La geodésica de velocidad unitaria que sube verticalmente, a través del punto i, está dada por

${displaystyle gamma (t)={begin{pmatrix}e^{t/2}&0\0&e^{-t/2}\end{pmatrix}}cdot i=ie^{t}.}$

Debido a que PSL(2,R) actúa transitivamente por isometrías del semiplano superior, esta geodésica se mapea en las otras geodésicas mediante la acción de PSL(2,R). Por lo tanto, la geodésica general de velocidad unitaria está dada por

${displaystyle gamma (t)={begin{pmatrix}a&b\c&d\end{pmatrix}}{begin{pmatrix}e^{t/2}&0\0&e^{-t/2}\end{pmatrix}}cdot i={frac {aie^{t}+b}{cie^{t}+d}}.}$

Esto proporciona una descripción básica del flujo geodésico en el haz tangente de longitud unitaria (haz de líneas complejas) en el semiplano superior. A partir de este modelo, se puede obtener el flujo en superficies arbitrarias de Riemann, como se describe en el artículo sobre el flujo de Anosov.

El modelo en tres dimensiones

La métrica del modelo en el medio espacio $0}}" xmlns="http://www.w3.org/1998/Math/MathML">{}.. x,Sí.,z.. ▪ ▪ z■0}{textstyle {langle x,y,zrangle mid }0}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c42a21c7556e044b2f1f15cd6073df5e969bed8a" style="vertical-align: -0.838ex; width:17.062ex; height:2.843ex;"/>$ es dado por

{displaystyle (ds)^{2}={frac {(dx)^{2}+(dy)^{2}+(dz)^{2}}{z^{2}}},}

donde s mide la longitud a lo largo de una línea posiblemente curva. Las líneas rectas en el espacio hiperbólico (geodésicas para este tensor métrico, es decir, curvas que minimizan la distancia) se representan en este modelo mediante arcos circulares normales al z = 0- plano (semicírculos cuyo origen está en el plano z = 0) y rayos verticales rectos normales al plano z = 0.

El distancia entre dos puntos ${textstyle p_{1}=langle x_{1},y_{1},z_{1}rangle }$ y ${textstyle p_{2}=langle x_{2},y_{2},z_{2}rangle }$ medido en esta métrica a lo largo de tal geodésico es:

{displaystyle operatorname {dist} (p_{1},p_{2})=2operatorname {arsinh} {frac {|p_{2}-p_{1}|}{2{sqrt {z_{1}z_{2}}}}}.}

El modelo en n dimensiones

Este modelo se puede generalizar para modelar $n+1$ espacio hiperbólico dimensional reemplazando el número real x por un vector en un n Espacio vectorial dimensional Euclidean.

Contenido relacionado

David Starr Jordan
David Starr Jordan fue el presidente fundador de la Universidad de Stanford y ocupó el cargo de 1891 a 1913. Fue ictiólogo durante su carrera de...
Walter H Schottky
Walter Hans Schottky fue un físico alemán que desempeñó un papel importante en el desarrollo de la teoría de los fenómenos de emisión de iones y...
Claritromicina
La claritromicina, comercializada bajo la marca Biaxin entre otras, es un antibiótico que se utiliza para tratar diversas infecciones bacterianas. Esto...
Más resultados...
Te puede interesar