Modelo de Ramsey-Cass-Koopmans

El modelo de Ramsey-Cass-Koopmans, o modelo de crecimiento de Ramsey, es un modelo neoclásico de crecimiento económico basado principalmente en el trabajo de Frank P. Ramsey, con ampliaciones significativas de David Cass y Tjalling Koopmans. El modelo de Ramsey-Cass-Koopmans difiere del modelo de Solow-Swan en que la elección del consumo está explícitamente microfundamentada en un punto en el tiempo y, por lo tanto, endogeniza la tasa de ahorro. Como resultado, a diferencia del modelo de Solow-Swan, la tasa de ahorro puede no ser constante a lo largo de la transición al estado estacionario de largo plazo. Otra implicación del modelo es que el resultado es Pareto óptimo o Pareto eficiente.

Originalmente, Ramsey planteó el modelo como un problema de planificación social que consistía en maximizar los niveles de consumo a lo largo de generaciones sucesivas. Solo más tarde Cass y Koopmans adoptaron un modelo como descripción de una economía dinámica descentralizada con un agente representativo. El modelo de Ramsey-Cass-Koopmans apunta únicamente a explicar el crecimiento económico a largo plazo, en lugar de las fluctuaciones del ciclo económico, y no incluye ninguna fuente de perturbaciones como imperfecciones del mercado, heterogeneidad entre los hogares o shocks exógenos. Por lo tanto, investigadores posteriores ampliaron el modelo, permitiendo shocks en las compras gubernamentales, variaciones en el empleo y otras fuentes de perturbaciones, lo que se conoce como teoría del ciclo económico real.

En la configuración habitual, el tiempo comienza continuamente, para la simplicidad, en ${\displaystyle t=0}$ y continuando para siempre. Por supuesto, los únicos factores productivos son el capital ${\displaystyle K}$ y el trabajo ${\displaystyle L.$, ambos requeridos para ser no negativo. Se supone que la fuerza laboral, que constituye a toda la población, crece a un ritmo constante ${\displaystyle n}$, es decir. ${\displaystyle {\dot {}={\tfrac {\mathrm} {\fnK} {\fnK} {\f}} {\fnK}}}} {\fnK}} {\fnK}}} {\fnK}}}} {\fnK}}}}} {\fnK\f}}}}}}}}}}}} {\f}}}}}}}}}}}}} {\m}}}}}}}}}}}}}}}}}}}}}}} {\tfrac\tfrac\tfrac\tfrac\m}}}}}}}}}}}}}}} {\tfrac\tfrac\tfrac\m} {\m\m\m\m\m\m\m\m\m\m\m\m\m}}}}\m\m\m\m\m}}m}m\m\m}m}m} {\m}m}} L}{\mathrm {d}=nL}$, implicando que ${\displaystyle L=L_{0}e^{nt}$ con nivel inicial ${\displaystyle L_{0} confía0}$ a ${\displaystyle t=0}$. Finalmente, vamos ${\displaystyle Sí.$ denota la producción agregada y ${\displaystyle C}$ denota el consumo agregado.

Las variables que el modelo Ramsey-Cass–Koopmans pretende describir en última instancia son ${\displaystyle c={\frac {C} {L}}$, el per cápita (o con más precisión, por trabajo) consumo, así como ${\displaystyle k={\frac {K}{L}}$, la llamada intensidad de capital. Lo hace por primera vez conectando la acumulación de capital, escrita ${\displaystyle {\dot {}={\tfrac {\mathrm} {\fnK}} {\fnK}}={\tfrac {\m} ¿Qué?$ en la notación de Newton, con consumo ${\displaystyle C}$, describiendo una compensación de consumo-inversión. Más concretamente, dado que las reservas de capital existentes se desintegran por la tasa de depreciación ${\displaystyle \delta }$ (según sea constante), requiere inversión de la producción de los períodos actuales ${\displaystyle Sí.$. Así, $${\displaystyle {\ dot {}=Y-\delta K-cL$$

La relación entre los factores productivos y la producción agregada se describe por la función de producción agregada, ${\displaystyle Y=F(K,L)}$. Una opción común es la función de producción de Cobb-Douglas ${\displaystyle F(K,L)=AK^{1-\alpha }L^{\alpha }$, pero generalmente cualquier función de producción que satisfaga las condiciones Inada es permisible. Es importante, sin embargo, ${\displaystyle F}$ es necesario ser homogéneo del grado 1, lo que implica económicamente retornos constantes a escala. Con esta suposición, podemos reexpresar la producción agregada en per cápita términos $${\displaystyle F(K,L)=L\cdot F\left({\frac {K}{L}},1\right)=L\cdot f(k)}$$ Por ejemplo, si utilizamos la función de producción de Cobb-Douglas con ${\displaystyle A=1,\alpha =0,5}$Entonces ${\displaystyle f(k)=k^{0.5}$.

Para obtener la primera ecuación clave del modelo Ramsey-Cass–Koopmans, la ecuación dinámica para el stock de capital debe expresarse en per cápita términos. Tomando nota de la regla de referencia ${\displaystyle {\tfrac {\mathrm} } {\mhm {d}}\left({\tfrac {K}\right)}$, tenemos

una ecuación diferencial no lineal similar al modelo de Solow-Swan.

Si ignoramos el problema de cómo se distribuye el consumo, entonces la tasa de utilidad ${\displaystyle U}$ es una función de consumo agregado. Eso es, ${\displaystyle U=U(C,t)}$. Para evitar el problema del infinito, descartamos exponencialmente la utilidad futura a una tasa de descuento ${\displaystyle \rho \in (0,\infty)}$. Un alto ${\displaystyle \rho }$ refleja alta impaciencia.

El problema del planificador social es maximizar la función de bienestar social ${\displaystyle U_{0}=\int ¿Qué?$.

Supongamos que la economía está poblada por individuos inmortales idénticos con funciones de utilidad inmutables ${\displaystyle u(c)}$ (a representative agent), such that the total util is:$${\displaystyle U(C,t)=Lu(c)=L_{0}e^{nt}u(c)}$$La función de utilidad se supone que está aumentando estrictamente (es decir, no hay punto de dicha) y concave en ${\displaystyle c}$Con ${\displaystyle \lim _{c\to ¿Qué?$, donde ${\displaystyle u_{c}$ es la utilidad marginal del consumo ${\displaystyle {\tfrac {\partial u}{\partial c}}$.

Tenemos, pues, el problema del planificador social:

${\displaystyle \max _{c}\int _{0}{\infty }e^{-(\rho -n)t}u(c)\,\mathrm {d} t}$

${\displaystyle {\text{subject to}\quad c=f(k)-(n+\delta)k-{\dot {k}}$

donde se encuentra una reserva inicial de capital no cero ${\displaystyle k(0)=k_{0} {0}]$ se da.

Para asegurar que la integral esté bien definida, imponemos ${\displaystyle \rho >n}$.

La solución, que normalmente se encuentra utilizando una función hamiltoniana, es una ecuación diferencial que describe la evolución óptima del consumo,

la regla de Keynes-Ramsey.

El término ${\displaystyle f_{k}(k)-\delta - ¿Qué?$, donde ${\displaystyle F_{k}=\partial ¿Qué?$ es el producto marginal del capital, refleja el rendimiento marginal de la inversión neta, contando la depreciación del capital y el descuento del tiempo.

Aquí. ${\displaystyle \sigma (c)}$ es la elasticidad de la sustitución intertemporal, definida por$${\displaystyle \sigma (c)=-{\frac {u_{c}(c)}{c\cdot u_{cc}(c)}}=-{\frac {d\ln c}{d\ln(u'(c)}}}}}$$Es formalmente equivalente a la inversa de la aversión relativa de riesgo. La cantidad refleja la curvatura de la función de utilidad e indica cuánto el agente representativo desea suavizar el consumo con el tiempo. Si el agente tiene una aversión de alto riesgo relativo, entonces tiene baja EIS, y por lo tanto estaría más dispuesto a suavizar el consumo con el tiempo.

A menudo se supone que ${\displaystyle u}$ es estrictamente monotonicamente creciente y concave, por lo tanto ${\displaystyle \sigma œ0}$. En particular, si la utilidad es logarítmica, entonces es constante:$${\displaystyle u(c)=u_{0}\ln c\implies \sigma (c)=1}$$Podemos reescribir la regla de Ramsey como$${\displaystyle \underbrace {\frac {d} {dt}\ln c} _{\text{=consumtion delay rate}}=\underbrace {\sigma (c)} _{\text{EIS at current consumption level}\quad }\underbrace {f_{k}(k)-\delta -\rho]} ################################################################################################################################################################################################################################################################$$donde interpretamos ${\displaystyle {\frac {dt}}\ln} c)$ como la "tasa de demora de consumo", porque si es alta, entonces significa que el agente consume mucho menos ahora en comparación con más tarde, que es esencialmente lo que el consumo retrasado es de.

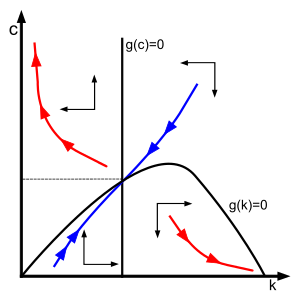
Las dos ecuaciones diferenciales unidas para ${\displaystyle k}$ y ${\displaystyle c}$ forman el sistema dinámico Ramsey-Cass–Koopmans.

Un estado estable ${\displaystyle (k^{\ast },c^{\ast }}$ para el sistema se encuentra mediante la configuración ${\displaystyle {\dot {}}}$ y ${\displaystyle {\ dot {c}}$ igual a cero. Hay tres soluciones:

${\displaystyle f_{k}\left(k^{\ast }\right)=\delta ##\rho \quad {\text{and}\quad c^{\ast }=f\left(k^{\ast }\right)-(n+\delta)k^{\ast }}$

${\displaystyle (0,0)}$

${\displaystyle f(k^{*})=(n+\delta)k^{*}{=0}$

La primera es la única solución en el interior del cuadrante superior. Es un punto de silla (como se muestra a continuación). La segunda es un punto de repulsión. La tercera es un equilibrio estable degenerado.

Por defecto, se tiene en cuenta la primera solución, aunque es importante tener en cuenta las otras dos.

Cualquier trayectoria óptima debe seguir el sistema dinámico. Sin embargo, desde la variable ${\displaystyle c}$ es una variable de control, en cada intensidad de capital ${\displaystyle k}$, para encontrar su trayectoria óptima correspondiente, todavía necesitamos encontrar su tasa de consumo inicial ${\displaystyle c(0)}$. Como resulta, la trayectoria óptima es la única que converge al punto de equilibrio interior. Cualquier otra trayectoria converge al equilibrio de todo ahorro con ${\displaystyle k^{*}}0,c^{*}=0}$, o se sumerge a ${\displaystyle k\to 0,c\to \infty }$, lo que significa que la economía gasta todo su capital en tiempo finito. Ambos logran una menor utilidad general que la trayectoria hacia el punto de equilibrio interior.

Declaración cualitativa sobre la estabilidad de la solución ${\displaystyle (k^{\ast },c^{\ast }}$ requiere una linearización por un polinomio Taylor de primer orden

${\\fnK}\\fnK}\\\fnK}\\\fnh}\fn}\fn}\fn}\cron}\cH0} \mathbf {J} (k^{\ast },c^{\ast }){\begin{bmatrix}(k-k^{\ast })\(c-c-c^{\ast })\end{bmatrix}}}}}}}}}}$

Donde ${\displaystyle \mathbf {J} (k^{\ast },c^{\ast }}}$ es la matriz Jacobiana evaluada en estado constante, dada por

${\displaystyle \mathbf {J} \left(k^{\ast },c^{\ast }\right)={\begin{bmatrix}\rho - ¿Qué? {1}{\sigma }f_{kk} k)\cdot c^{\ast } {0\end{bmatrix}}}$

que tiene determinante ${\displaystyle \left WordPress\mathbf {J} \left(k^{\ast },c^{\ast }\right)\right durable={\frac {1}{\sigma ¿Qué?$ desde entonces ${\displaystyle c^{*}}0}$ ${\displaystyle \sigma }$ es positivo por suposición, y ${\displaystyle f_{kk}traducido0}$ desde entonces ${\displaystyle f}$ es concave (condición inada). Dado que el determinante es igual al producto de los eigenvalues, los eigenvalues deben ser reales y opuestos en señal.

Por lo tanto, según el teorema de la variedad estable, el equilibrio es un punto de silla y existe un único brazo estable, o “camino de silla”, que converge hacia el equilibrio, indicado por la curva azul en el diagrama de fases.

El sistema se denomina “saddle path stable” (trayectoria de silla de montar) ya que todas las trayectorias inestables quedan descartadas por la condición de “no esquema Ponzi”:

${\displaystyle \lim _{t\to \infty }k\cdot e^{-\int _{0} {t}\left(f_{k}-n-\delta \right)\mathrm {d}\geq 0}$

lo que implica que el valor actual del stock de capital no puede ser negativo.

Spear y Young reexaminan la historia del crecimiento óptimo durante los años 1950 y 1960, centrándose en parte en la veracidad del supuesto desarrollo simultáneo e independiente de "Optim growth in an gregative model of capital acquisition" (crecimiento óptimo en un modelo agregado de acumulación de capital) de Cass (publicado en 1965 en la Review of Economic Studies) y "On the concept of optimal economic growth" (sobre el concepto de crecimiento económico óptimo) de Tjalling Koopman (publicado en Study Week on the Econometric Approach to Development Planning, 1965, Roma: Pontificia Academia de Ciencias).

A lo largo de sus vidas, ni Cass ni Koopmans sugirieron nunca que sus resultados que caracterizaban el crecimiento óptimo en el modelo de crecimiento continuo en un sector fueran otra cosa que "simultáneos e independientes". El hecho de que la cuestión de la prioridad se convirtiera en un punto de discusión se debió únicamente al hecho de que en la versión publicada del trabajo de Koopmans, citó el capítulo de la tesis de Cass que más tarde se convirtió en el artículo de RES. En su artículo, Koopmans afirma en una nota a pie de página que Cass obtuvo de forma independiente condiciones similares a las que encuentra Koopmans, y que Cass también considera el caso límite en el que la tasa de descuento tiende a cero en su artículo. Por su parte, Cass señala que "después de que se completó la versión original de este artículo, nos llamó la atención un análisis muy similar de Koopmans. Nos basamos en sus resultados al analizar el caso límite, en el que la tasa de descuento social efectiva tiende a cero". En la entrevista que Cass dio a Macroeconomic Dynamics, le da crédito a Koopmans por haberle indicado el trabajo previo de Frank Ramsey, y afirma que se sintió avergonzado por no haberlo conocido, pero no dice nada que desmienta la afirmación básica de que su trabajo y el de Koopmans eran, de hecho, independientes.

Spear y Young cuestionan esta historia, basándose en una versión del documento de trabajo de Koopmans que se pasó por alto anteriormente y que fue la base de la presentación de Koopmans, citada con frecuencia, en una conferencia celebrada por la Academia Pontificia de Ciencias en octubre de 1963. En este documento de discusión de Cowles hay un error. Koopmans afirma en su resultado principal que las ecuaciones de Euler son necesarias y suficientes para caracterizar las trayectorias óptimas en el modelo porque cualquier solución a las ecuaciones de Euler que no converja al estado estable óptimo alcanzaría un límite de consumo cero o de capital cero en un tiempo finito. Este error aparentemente se presentó en la conferencia del Vaticano, aunque en el momento en que Koopmans lo presentó, ningún participante comentó sobre el problema. Esto se puede inferir porque la discusión después de cada presentación de documento en la conferencia del Vaticano se conserva textualmente en el volumen de la conferencia.

En la discusión del volumen del Vaticano que siguió a la presentación de un trabajo de Edmond Malinvaud, el problema surge debido a la inclusión explícita por parte de Malinvaud de una denominada "condición de transversalidad" (a la que Malinvaud llama Condición I) en su trabajo. Al final de la presentación, Koopmans le pregunta a Malinvaud si no es cierto que la Condición I simplemente garantiza que las soluciones de las ecuaciones de Euler que no convergen al estado estable óptimo alcanzan un límite en un tiempo finito. Malinvaud responde que no es así y sugiere que Koopmans observe el ejemplo con funciones de utilidad logarítmica y funciones de producción Cobb-Douglas.

En este punto, Koopmans obviamente reconoce que tiene un problema, pero, basándose en un apéndice confuso de una versión posterior del documento producido después de la conferencia del Vaticano, parece incapaz de decidir cómo abordar la cuestión planteada por la Condición I de Malinvaud.

De la entrevista con Cass en Dinámica macroeconómica se desprende claramente que Koopmans se reunió con el asesor de tesis de Cass, Hirofumi Uzawa, en las reuniones de invierno de la Sociedad Econométrica en enero de 1964, donde Uzawa le informó de que su estudiante [Cass] ya había resuelto este problema. Uzawa debe haberle proporcionado entonces a Koopmans la copia del capítulo de la tesis de Cass, que aparentemente envió bajo la apariencia del Informe técnico del IMSSS que Koopmans citó en la versión publicada de su artículo. La palabra "disfraz" es apropiada aquí, porque el número de TR que aparece en la cita de Koopmans habría situado la fecha de publicación del informe a principios de los años 1950, lo que claramente no era así.

En la versión publicada del artículo de Koopmans, éste impone una nueva condición Alfa además de las ecuaciones de Euler, afirmando que las únicas trayectorias admisibles entre las que satisfacen las ecuaciones de Euler son las que convergen al equilibrio óptimo en estado estacionario del modelo. Este resultado se deriva en el artículo de Cass mediante la imposición de una condición de transversalidad que Cass dedujo de secciones relevantes de un libro de Lev Pontryagin. Spear y Young conjeturan que Koopmans tomó esta ruta porque no quería que pareciera que estaba "tomando prestada" la tecnología de transversalidad de Malinvaud o de Cass.

Basándose en este y otros análisis de las contribuciones de Malinvaud en la década de 1950 (en particular, su intuición de la importancia de la condición de transversalidad), Spear y Young sugieren que el modelo de crecimiento neoclásico podría llamarse mejor modelo Ramsey-Malinvaud-Cass en lugar del título honorífico establecido Ramsey-Cass-Koopmans.

• Acemoglu, Daron (2009). "El modelo de crecimiento neoclásico". Introducción al crecimiento económico moderno. Princeton: Princeton University Press. pp. 287–326. ISBN 978-0-691-13292-1.
• Barro, Robert J.; Sala-i-Martin, Xavier (2004). "Modelos de crecimiento con optimización del consumidor". Crecimiento económico (Segunda edición). Nueva York: McGraw-Hill. pp. 85–142. ISBN 978-0-262-02553-9.
• Bénassy, Jean-Pascal (2011). "El modelo Ramsey". macroeconómica Teoría. New York: Oxford University Press. pp. 145–160. ISBN 978-0-19-538771-1.
• Blanchard, Olivier Jean; Fischer, Stanley (1989). "Consumo e Inversión: Modelos Horizon Infinitos Básicos". Conferencias sobre Macroeconomía. Cambridge: MIT Press. pp. 37–89. ISBN 978-0-262-02283-5.
• Miao, Jianjun (2014). "Modelos de crecimiento neoclásicos". Dinámica económica en tiempo discreto. Cambridge: MIT Press. pp. 353–364. ISBN 978-0-262-02761-8.
• Novales, Alfonso; Fernández, Esther; Ruíz, Jesús (2009). "Crecimiento óptimo: Análisis del tiempo continuo". Crecimiento Económico: Teoría y métodos de solución numérica. Berlín: Springer. pp. 101–154. ISBN 978-3-540-68665-1.
• Romer, David (2011). "Infinite-Horizon and Overlapping-Generations Models". Macroeconómico avanzado (Cuarta edición). Nueva York: McGraw-Hill. pp. 49–77. ISBN 978-0-07-351137-5.

• Discusión del documento original de Ramsey por Orazio Attanasio en YouTube