Modelo de difusión de graves

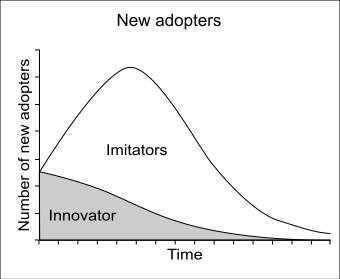
El modelo de Bass o modelo de difusión de Bass fue desarrollado por Frank Bass. Consiste en una ecuación diferencial simple que describe el proceso de adopción de nuevos productos en una población. El modelo presenta una lógica de cómo interactúan los adoptantes actuales y los adoptantes potenciales de un nuevo producto. La premisa básica del modelo es que los adoptantes pueden clasificarse como innovadores o imitadores, y la velocidad y el momento de la adopción dependen de su grado de innovación y del grado de imitación entre los adoptantes. El modelo de Bass se ha utilizado ampliamente en la previsión, especialmente en la previsión de ventas de nuevos productos y en la previsión de tecnología. Matemáticamente, la difusión básica de Bass es una ecuación de Riccati con coeficientes constantes equivalentes al crecimiento logístico de Verhulst-Pearl.

En 1969, Frank Bass publicó su artículo sobre un nuevo modelo de crecimiento de productos para bienes de consumo duraderos. Antes de esto, Everett Rogers publicó Difusión de innovaciones, un trabajo muy influyente que describía las diferentes etapas de la adopción de un producto. Bass aportó algunas ideas matemáticas al concepto. Mientras que el modelo de Rogers describe las cuatro etapas del ciclo de vida del producto (Introducción, Crecimiento, Madurez, Declive), el modelo de Bass se centra en las dos primeras (Introducción y Crecimiento). Algunas de las extensiones del modelo de Bass presentan modelos matemáticos para las dos últimas (Madurez y Declive).

${\displaystyle {\frac {f(t)}{1-F(t)}=p+qF(t)}$

Dónde:

• ${\displaystyle \ F(t)}$ es la fracción base instalada
• ${\displaystyle \ f(t)}$ es la tasa de cambio de la fracción base instalada, es decir,${\displaystyle \ f(t)=F'(t)}$
• ${\displaystyle \ p}$ es el coeficiente de innovación
• ${\displaystyle \ q}$ es el coeficiente de imitación

Expresada como una ecuación diferencial ordinaria,

${\displaystyle {\frac {dF}{dt}=p(1-F)+q(1-F)F=(1-F)(p+qF)=p-F(p-q)-qF^{2}$

Ventas (o nuevos adoptantes)${\displaystyle \ s(t)}$ a la vez${\displaystyle\ t}$ es la tasa de cambio de la base instalada, es decir,${\displaystyle \ f(t)}$ multiplicado por el potencial de mercado final${\displaystyle \ m}$. Bajo la condición${\displaystyle \ F(0)=0}$, tenemos eso

${\displaystyle \ s(t)=mf(t)}$

${\displaystyle \ s(t)=m{(p+q)}{2}{p}{\frac {-(p+q)t}{(1+{\frac {q} {p}}e^{-(p+q)t}}}}}{2}}}}}}}}}}}}}}}}}}}}} {}}}}}} {} {}}}}}}}}}}}}}}} {}}} {}}}}}} {}}}}}} {}}}}} {}}}}}}}}} {}}}}}}} {}}}}}}}}}}}}}}}}}}}}}} {}}}}}}}}}}}}} {\$

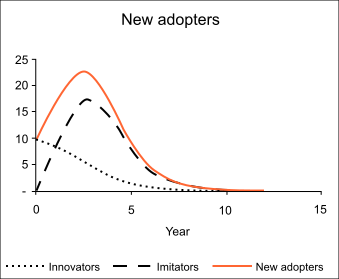
Tenemos la descomposición${\displaystyle \ s(t)=s_{n}(t)+s_{i}(t)}$ Donde${\displaystyle \ s_{n}(t):=mp(1-F(t)}$ es el número de innovadores a la vez${\displaystyle\ t}$, y${\displaystyle \ s_{i}(t):=mq(1-F(t))F(t)}$ es el número de imitadores a la vez${\displaystyle\ t}$.

El tiempo de las ventas máximas${\displaystyle \ t^{*}$:

${\displaystyle \ t^{*}={\frac {\ln q-\ln {}}}}$

Los tiempos de la inflexión apuntan a la curva de los nuevos adoptantes${\displaystyle\ t^{}}$:

${\displaystyle \ t^{**}={\frac {\ln(q/p)-\ln(2\pm {\sqrt {3})} {p+q}} {}} {}}} {}}} {}} {}}} {}} {}} {}}} {}}}}}} {}}}}} {}}}} {}}}} {}}}} {}}} {}}}} {}}}}}} {}}}}}} {}}}}}}}} {} {}}}}}}} {}}}}} {}}}} {}}} {}}}}}}}}} {}}}}}} {} {}}}}} {}}}}}} {}}}}} {}}}}}} {}}}}}} {} {} {} {}}}} {} {}}}}}}}}}}}} {}}}}} {}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}$

o en otra forma (relacionada con el pico de ventas):

${\displaystyle \ t^{}=t^{*}\pm #frac {\ln(2+{\sqrt {3})} {p+q}} {}} {}}} {}}} {}} {}}} {}} {}} {}}} {}}}}}} {}}}}} {}}}} {}}}} {}}}} {}}} {}}}} {}}}}}} {}}}}}} {}}}}}}}} {} {}}}}}}} {}}}}} {}}}} {}}} {}}}}}}}}} {}}}}}} {} {}}}}} {}}}}}} {}}}}} {}}}}}} {}}}}}} {} {} {} {}}}} {} {}}}}}}}}}}}} {}}}}} {}}}}}} {}}}}}}}}}}}} {}}}}}}}}}}} {}}}}}}}}}}}}}}}$

El tiempo máximo y los tiempos de inflexión deben ser positivos. Cuando${\displaystyle \ t^{*}$ es negativo, las ventas no tienen pico (y disminución desde la introducción). Hay casos (dependiendo de los valores de${\displaystyle \ p}$ y${\displaystyle \ q}$) cuando la curva de los nuevos adoptantes (que comienza a 0) tiene sólo uno o cero puntos de inflexión.

El coeficiente${\displaystyle \ p}$ se llama coeficiente de innovación, influencia externa o efecto publicitario. El coeficiente${\displaystyle \ q}$ se llama el coeficiente de imitación, influencia interna o efecto palabra de boca.

Valores típicos de${\displaystyle \ p}$ y${\displaystyle \ q}$ cuando${\displaystyle\ t}$ se mide en años:

• El valor medio de${\displaystyle \ p}$ ha sido encontrado a 0.03, con un rango típico entre 0.01 y 0.03.
• El valor medio de${\displaystyle \ q}$ se ha encontrado en 0,38, con un rango típico entre 0,3 y 0,5.

El modelo de difusión Bass se deriva asumiendo que la tasa de peligro ${\displaystyle \lambda (t)}$ para la ingesta de un producto o servicio se puede definir como:$${\displaystyle \lambda (t)={f(t) \over {S(t)}=p+q[1-S(t)}$$Donde ${\displaystyle f(t)}$ es la función de densidad de probabilidad y ${\displaystyle S(t)=1-F(t)}$ es la función de supervivencia, con ${\displaystyle F(t)}$ siendo la función de distribución acumulativa. De estas definiciones básicas en análisis de supervivencia, sabemos que:$${\displaystyle f(t)=-{d S \over {dt}\implies \lambda (t)=-{1 \over {S}{d S \over {dt}}$$Por lo tanto, la ecuación diferencial para la función de supervivencia es equivalente a:$${\displaystyle {dS \over {S[p+q(1-S)}=-dt}$$La integración y reorganización de términos nos da que:$${\displaystyle {S \over {p+q(1-S)}=Ae^{-(p+q)t}$$Para cualquier función de supervivencia, debemos tenerlo ${\displaystyle S(0)=1}$ y esto implica que ${\displaystyle A=p^{-1}$. Con esta condición, la función de supervivencia es:$${\displaystyle S(t)={-(p+q)t}+{q \over {p}e^{-(p+q)t} \over {1+{q\over {p}e^{-(p+q)t}}}}}} {}}}}} {\f}}}}$$Finalmente, utilizando el hecho de que ${\displaystyle F(t)=1-S(t)}$, encontramos que el modelo de difusión Bass para la absorción de productos es:$${\displaystyle F(t)={1-e^{-(p+q)t}\over {1+{q \over {p}e^{-(p+q)t}}}} {}} {\cHFF}$$

Bass descubrió que su modelo se ajustaba a los datos de casi todas las presentaciones de productos, a pesar de una amplia gama de variables de decisión gerencial, por ejemplo, precios y publicidad. Esto significa que las variables de decisión pueden cambiar la curva de Bass con el tiempo, pero que la forma de la curva siempre es similar.

Aunque se han propuesto muchas extensiones del modelo, sólo una de ellas se reduce al modelo de Bass en circunstancias ordinarias.

Este modelo fue desarrollado en 1994 por Frank Bass, Trichy Krishnan y Dipak Jain:

${\displaystyle {\frac {f(t)}{1-F(t)}=(p+{q}F(t)x(t)}$

Donde ${\displaystyle \ x(t)}$ es una función de cambio porcentual en el precio y otras variables

A diferencia del modelo de Bass, que tiene una solución analítica pero también se puede resolver numéricamente, los modelos de Bass generalizados normalmente no tienen soluciones analíticas y se deben resolver numéricamente. Orbach (2016) señala que los valores de p,q no son perfectamente idénticos para las formas de tiempo continuo y tiempo discreto. Para los casos comunes (donde p está dentro del rango de 0,01-0,03 y q dentro del rango de 0,2-0,4) los pronósticos de tiempo discreto y tiempo continuo son muy cercanos. Para otros valores de p,q los pronósticos pueden diferir significativamente.

Los productos tecnológicos se suceden uno tras otro a lo largo de generaciones. Norton y Bass ampliaron el modelo en 1987 para las ventas de productos con compras repetidas continuas. La formulación para tres generaciones es la siguiente:

${\displaystyle S_{1,t}=F(t_{1})m_{1}(1-F(t_{2})}}$

${\displaystyle \ S_{2,t}=F(t_{2})(m_{2}+F(t_{1})m_{1})(1-F(t_{3})}$

${\displaystyle \ S_{3,t}=F(t_{3})(m_{3}+F(t_{2})(m_{2}+F(t_{1})m_{1})}}$

donde

• ${\displaystyle \ m_{i}=a_{i}M_{i}$
• ${\displaystyle \ M_{i}$ es el número incremental de los adoptantes finales de los iproducto de generación
• ${\displaystyle \ a_{i}$ es el promedio (continua) tasa de compra de repetición entre los adoptantes del iproducto de generación
• ${\displaystyle \ t_{i}$ es el momento desde la introducción de la iproducto de generación
• ${\displaystyle \ F(t_{i})={\frac {1-e^{-(p+q)t_{i}}{1+{\frac {\fnMicrosoft Sans Serif}$

Se ha descubierto que los términos p y q son generalmente los mismos entre generaciones sucesivas.

Existen dos casos especiales del modelo de difusión de Bass.

• El primer caso especial ocurre cuando q=0, cuando el modelo se reduce a la distribución exponencial.
• El segundo caso especial se reduce a la distribución logística, cuando p=0.

El modelo de Bass es un caso especial de la distribución de Gompertz Gamma/Desplazada (G/SG): Bemmaor (1994)

El rápido crecimiento reciente (a principios de 2007) de las redes sociales en línea (y otras comunidades virtuales) ha llevado a un mayor uso del modelo de difusión de Bass. El modelo de difusión de Bass se utiliza para estimar el tamaño y la tasa de crecimiento de estas redes sociales. El trabajo de Christian Bauckhage y coautores muestra que el modelo de Bass proporciona una imagen más pesimista del futuro que otros modelos alternativos, como la distribución de Weibull y la distribución de Gompertz desplazada.

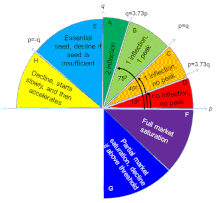
Bass (1969) distinguió entre un caso de p<q en el que las ventas periódicas crecen y luego declinan (un producto exitoso tiene un pico de ventas periódico); y un caso de p>q en el que las ventas periódicas declinan desde el lanzamiento (no hay pico).

Jain et al. (1995) exploraron el impacto de la siembra. Cuando se utiliza la siembra, la difusión puede comenzar cuando p + qF(0) > 0 incluso si el valor de p es negativo, pero un vendedor utiliza la estrategia de siembra con un tamaño de semilla de F(0) > -p/q. La interpretación de un valor de p negativo no significa necesariamente que el producto sea inútil: puede haber casos en los que existan barreras de precio o esfuerzo para la adopción cuando muy pocos otros ya lo hayan hecho. Cuando otros adoptan, los beneficios del producto aumentan, debido a externalidades o reducción de la incertidumbre, y el producto se vuelve cada vez más plausible para muchos clientes potenciales.

Moldovan y Goldenberg (2004) incorporaron el efecto de boca en boca (WOM) negativo en la difusión, lo que implica una posibilidad de q negativa. Una q negativa no significa necesariamente que los adoptantes estén decepcionados e insatisfechos con su compra. Puede encajar en un caso en el que el beneficio de un producto disminuye a medida que más personas lo adoptan. Por ejemplo, para un cierto nivel de demanda de viajes en tren, se pueden vender billetes reservados a quienes desean garantizar un asiento. Aquellos que no reservan asientos pueden tener que viajar de pie. A medida que se venden más asientos reservados, se reduce la aglomeración en el vagón de tren sin reserva y aumenta la probabilidad de encontrar un asiento en el vagón sin reserva, lo que reduce el incentivo para comprar asientos reservados. Si bien la curva de ventas no acumulativa con q negativa es similar a aquellas con q=0, la curva de ventas acumulativa presenta una situación más interesante: cuando p > -q, el mercado alcanzará el 100% de su potencial, eventualmente, como para un valor positivo regular de q. Sin embargo, si p < -q, en el largo plazo, el mercado se saturará en un nivel de equilibrio –p/q de su potencial.

Orbach (2022) resumió el comportamiento de la difusión en cada porción del espacio p,q y mapea las regiones extendidas (p,q) más allá del cuadrante derecho positivo (donde la difusión es espontánea) a otras regiones donde la difusión enfrenta barreras (p negativo), donde la difusión requiere “estímulos” para comenzar, o resistencia de los adoptantes a nuevos miembros (q negativo), lo que podría estabilizar el mercado por debajo de la adopción total.

El modelo es una de las generalizaciones empíricas más citadas en marketing; en agosto de 2023, el artículo "A New Product Growth for Model Consumer Durables" publicado en Management Science tenía (aproximadamente) 11352 citas en Google Scholar.

Este modelo ha tenido una gran influencia en la ciencia del marketing y la gestión. En 2004 fue seleccionado como uno de los diez artículos más citados en los 50 años de historia de la ciencia de la gestión. Ocupó el puesto número cinco y fue el único artículo de marketing de la lista. Posteriormente se reimprimió en la edición de diciembre de 2004 de la ciencia de la gestión.

El modelo de Bass fue desarrollado para bienes de consumo duraderos. Sin embargo, también se ha utilizado para pronosticar la aceptación en el mercado de numerosos productos y servicios de consumo e industriales, incluidos productos tangibles, intangibles, médicos y financieros. Sultan et al. (1990) aplicaron el modelo de Bass a 213 categorías de productos, principalmente bienes de consumo duraderos (en una amplia gama de precios), pero también a servicios como moteles y productos industriales/agrícolas como semillas de maíz híbrido.

• Difusión de la innovación
• Predicción
• Modelo de usuario perezoso
• Distribución Shifted Gompertz