Modelado de dispersión atmosférica

Modelado de dispersión atmosférica es la simulación matemática de cómo los contaminantes del aire se dispersan en la atmósfera ambiental. Se realiza con programas informáticos que incluyen algoritmos para resolver las ecuaciones matemáticas que rigen la dispersión de los contaminantes. Los modelos de dispersión se utilizan para estimar la concentración ambiental a favor del viento de contaminantes del aire o toxinas emitidas por fuentes tales como plantas industriales, tráfico vehicular o emisiones químicas accidentales. También se pueden utilizar para predecir concentraciones futuras en escenarios específicos (es decir, cambios en las fuentes de emisión). Por lo tanto, son el tipo dominante de modelo utilizado en la formulación de políticas de calidad del aire. Son más útiles para los contaminantes que se dispersan a grandes distancias y que pueden reaccionar en la atmósfera. Para contaminantes que tienen una variabilidad espacio-temporal muy alta (es decir,

Los modelos de dispersión son importantes para las agencias gubernamentales encargadas de proteger y gestionar la calidad del aire ambiental. Los modelos generalmente se emplean para determinar si las instalaciones industriales existentes o propuestas cumplen o cumplirán con los Estándares Nacionales de Calidad del Aire Ambiental (NAAQS) en los Estados Unidos y otras naciones. Los modelos también sirven para ayudar en el diseño de estrategias de control eficaces para reducir las emisiones de contaminantes atmosféricos nocivos. A fines de la década de 1960, la Oficina de Control de la Contaminación del Aire de la EPA de EE. UU. inició proyectos de investigación que conducirían al desarrollo de modelos para uso de planificadores urbanos y de transporte. Una aplicación importante y significativa de un modelo de dispersión de carreteras que resultó de dicha investigación se aplicó a Spadina Expressway de Canadá en 1971.

Los modelos de dispersión de aire también son utilizados por los servicios de seguridad pública y el personal de gestión de emergencias para la planificación de emergencia de escapes químicos accidentales. Los modelos se utilizan para determinar las consecuencias de los escapes accidentales de materiales peligrosos o tóxicos. Los escapes accidentales pueden provocar incendios, derrames o explosiones que involucren materiales peligrosos, como productos químicos o radionúclidos. Los resultados del modelado de dispersión, utilizando los términos fuente de liberación accidental y las condiciones meteorológicas en el peor de los casos, pueden proporcionar una estimación de la ubicación de las áreas afectadas, las concentraciones ambientales y utilizarse para determinar las medidas de protección adecuadas en caso de que se produzca una liberación. Las acciones de protección apropiadas pueden incluir la evacuación o el refugio en el lugar para las personas en la dirección del viento. En instalaciones industriales,

Los modelos de dispersión varían según las matemáticas utilizadas para desarrollar el modelo, pero todos requieren la entrada de datos que pueden incluir:

• Condiciones meteorológicas como la velocidad y dirección del viento, la cantidad de turbulencia atmosférica (caracterizada por lo que se denomina "clase de estabilidad"), la temperatura del aire ambiente, la altura hasta el fondo de cualquier inversión en altura que pueda estar presente, la cobertura de nubes y radiación solar.
• Término fuente (la concentración o cantidad de toxinas en términos fuente de emisión o liberación accidental) y temperatura del material
• Emisiones o parámetros de liberación como ubicación y altura de la fuente, tipo de fuente (es decir, fuego, piscina o chimenea de ventilación) y velocidad de salida, temperatura de salida y tasa de flujo másico o tasa de liberación.
• Elevaciones del terreno en la ubicación de origen y en las ubicaciones receptoras, como casas, escuelas, empresas y hospitales cercanos.
• La ubicación, la altura y el ancho de cualquier obstrucción (como edificios u otras estructuras) en el camino de la pluma gaseosa emitida, la rugosidad de la superficie o el uso de un parámetro más genérico de terreno "rural" o "urbano".

Muchos de los programas modernos y avanzados de modelado de dispersión incluyen un módulo de preprocesador para la entrada de datos meteorológicos y de otro tipo, y muchos también incluyen un módulo de posprocesador para graficar los datos de salida y/o trazar el área afectada por los contaminantes del aire en mapas Los gráficos de las áreas afectadas también pueden incluir isopletas que muestren áreas de concentraciones mínimas a altas que definen áreas de mayor riesgo para la salud. Los diagramas de isopletas son útiles para determinar las acciones de protección para el público y el personal de respuesta.

Los modelos de dispersión atmosférica también se conocen como modelos de difusión atmosférica, modelos de dispersión del aire, modelos de calidad del aire y modelos de dispersión de la contaminación del aire.

Capas atmosféricas

Es necesario analizar las capas de la atmósfera terrestre para comprender dónde se dispersan los contaminantes transportados por el aire en la atmósfera. La capa más cercana a la superficie de la Tierra se conoce como troposfera. Se extiende desde el nivel del mar hasta una altura de unos 18 km y contiene alrededor del 80 por ciento de la masa total de la atmósfera. La estratosfera es la siguiente capa y se extiende desde 18 km hasta unos 50 km. La tercera capa es la mesosfera que se extiende desde 50 km hasta unos 80 km. Hay otras capas por encima de los 80 km, pero son insignificantes con respecto al modelado de dispersión atmosférica.

La parte más baja de la troposfera se denomina capa límite atmosférica (ABL) o capa límite planetaria (PBL). La temperatura del aire de la atmósfera disminuye con el aumento de la altitud hasta que alcanza lo que se llama una capa de inversión (donde la temperatura aumenta con el aumento de la altitud) que cubre la capa límite convectiva, típicamente a alrededor de 1,5 a 2,0 km de altura. La parte superior de la troposfera (es decir, por encima de la capa de inversión) se denomina troposfera libre.y se extiende hasta la tropopausa (el límite en la atmósfera terrestre entre la troposfera y la estratosfera). En latitudes tropicales y medias durante el día, la capa convectiva libre puede comprender toda la troposfera, que es de 10 km a 18 km en la zona de convergencia intertropical.

El ABL es de los más importantes con respecto a la emisión, transporte y dispersión de contaminantes en el aire. La parte de la ABL entre la superficie de la Tierra y el fondo de la capa de inversión se conoce como capa de mezcla. Casi todos los contaminantes transportados por el aire emitidos a la atmósfera ambiental son transportados y dispersados ​​dentro de la capa de mezcla. Algunas de las emisiones penetran en la capa de inversión y entran en la troposfera libre por encima de la ABL.

En resumen, las capas de la atmósfera terrestre desde la superficie del suelo hacia arriba son: la ABL compuesta por la capa de mezcla cubierta por la capa de inversión; la troposfera libre; la estratosfera; la mesosfera y otros. Muchos modelos de dispersión atmosférica se conocen como modelos de capa límite porque principalmente modelan la dispersión de contaminantes del aire dentro de la ABL. Para evitar confusiones, los modelos denominados modelos de mesoescala tienen capacidades de modelado de dispersión que se extienden horizontalmente hasta unos pocos cientos de kilómetros. No quiere decir que modelen la dispersión en la mesosfera.

Ecuación de dispersión de contaminantes atmosféricos de Gauss

La literatura técnica sobre la dispersión de la contaminación del aire es bastante extensa y se remonta a la década de 1930 y antes. Una de las primeras ecuaciones de dispersión de la pluma de contaminantes del aire fue derivada por Bosanquet y Pearson. Su ecuación no asumió una distribución gaussiana ni incluyó el efecto del reflejo en el suelo de la pluma contaminante.

Sir Graham Sutton derivó una ecuación de dispersión de la pluma de contaminantes del aire en 1947 que incluía la suposición de una distribución gaussiana para la dispersión vertical y de viento cruzado de la pluma y también incluía el efecto de la reflexión en el suelo de la pluma.

Bajo el estímulo provisto por el advenimiento de regulaciones estrictas de control ambiental, hubo un inmenso crecimiento en el uso de cálculos de dispersión de penachos de contaminantes del aire entre fines de la década de 1960 y la actualidad. Durante ese período se desarrollaron una gran cantidad de programas informáticos para calcular la dispersión de las emisiones de contaminantes atmosféricos, a los que se denominó "modelos de dispersión atmosférica". La base para la mayoría de esos modelos fue la Ecuación completa para el modelado de dispersión gaussiana de penachos de contaminación de aire flotantes y continuos que se muestra a continuación:

dónde:
	= parámetro de dispersión del viento cruzado
	=
	= parámetro de dispersión vertical =
	= dispersión vertical sin reflejos
	=
	= dispersión vertical por reflexión desde el suelo
	=
	= dispersión vertical por reflexión de una inversión en altura
	=
	= concentración de emisiones, en g/m³, en cualquier receptor ubicado:
	x metros a favor del viento desde el punto de origen de la emisión
	y metros de viento cruzado desde la línea central del penacho de emisión
	z metros sobre el nivel del suelo
	= tasa de emisión del contaminante fuente, en g/s
	= velocidad horizontal del viento a lo largo de la línea central de la pluma, m/s
	= altura de la línea central de la pluma de emisión sobre el nivel del suelo, en m
	= desviación estándar vertical de la distribución de emisiones, en m
	= desviación estándar horizontal de la distribución de emisiones, en m
	= altura desde el nivel del suelo hasta la parte inferior de la inversión en altura, en m
	= la función exponencial

La ecuación anterior no solo incluye la reflexión hacia arriba desde el suelo, sino que también incluye la reflexión hacia abajo desde la parte inferior de cualquier tapa de inversión presente en la atmósfera.

La suma de los cuatro términos exponenciales en converge a un valor final con bastante rapidez. Para la mayoría de los casos, la suma de la serie con m = 1, m = 2 y m = 3 proporcionará una solución adecuada.

y son funciones de la clase de estabilidad atmosférica (es decir, una medida de la turbulencia en la atmósfera ambiente) y de la distancia a favor del viento hasta el receptor. Las dos variables más importantes que afectan al grado de dispersión de las emisiones contaminantes obtenidas son la altura del punto de emisión y el grado de turbulencia atmosférica. Cuanta más turbulencia, mejor es el grado de dispersión.

Las ecuaciones para y son:

(x) = exp(I _y + J _y ln(x) + K _y [ln(x)])

(x) = exp(I _z + J _z ln(x) + K _z [ln(x)])

(las unidades de , y , y x están en metros)

Coeficiente	A	B	C	D	mi	F
yo _	-1.104	-1.634	-2.054	-2.555	-2.754	-3.143
s s	0.9878	1.0350	1.0231	1.0423	1.0106	1.0148
K y	-0.0076	-0.0096	-0.0076	-0.0087	-0.0064	-0.0070
y z	4.679	-1.999	-2.341	-3.186	-3.783	-4.490
Jz _	-1.7172	0.8752	0.9477	1.1737	1.3010	1.4024
Kz _	0.2770	0.0136	-0.0020	-0.0316	-0.0450	-0.0540

La clasificación de clase de estabilidad es propuesta por F. Pasquill. Las seis clases de estabilidad se denominan: A-extremadamente inestable B-moderadamente inestable C-ligeramente inestable D-neutro E-ligeramente estable F-moderadamente estable

Los cálculos resultantes para las concentraciones de contaminantes del aire a menudo se expresan como un mapa de contorno de concentración de contaminantes del aire para mostrar la variación espacial en los niveles de contaminantes en un área amplia bajo estudio. De esta manera, las líneas de contorno pueden superponerse a ubicaciones de receptores sensibles y revelar la relación espacial de los contaminantes del aire con las áreas de interés.

Mientras que los modelos más antiguos se basan en clases de estabilidad (consulte la terminología de dispersión de la contaminación del aire) para la determinación de y , los modelos más recientes se basan cada vez más en la teoría de similitud de Monin-Obukhov para derivar estos parámetros.

Ecuaciones de ascenso de la pluma de Briggs

La ecuación de dispersión de contaminantes del aire de Gauss (discutida anteriormente) requiere la entrada de H, que es la altura de la línea central de la pluma de contaminantes sobre el nivel del suelo, y H es la suma de H _s (la altura física real del punto de origen de la emisión de la pluma de contaminantes) más Δ H (el penacho sube debido a la flotabilidad del penacho).

Para determinar Δ H, muchos, si no la mayoría, de los modelos de dispersión de aire desarrollados entre finales de la década de 1960 y principios de la de 2000 utilizaron lo que se conoce como "ecuaciones de Briggs". GA Briggs publicó por primera vez sus observaciones y comparaciones sobre el ascenso del penacho en 1965. En 1968, en un simposio patrocinado por CONCAWE (una organización holandesa), comparó muchos de los modelos de ascenso del penacho disponibles en la literatura. En ese mismo año, Briggs también escribió la sección de la publicación editada por Slade que trata sobre los análisis comparativos de los modelos de ascenso de la pluma. Eso fue seguido en 1969 por su revisión crítica clásica de toda la literatura sobre el ascenso del penacho,en el que propuso un conjunto de ecuaciones de ascenso de la pluma que se conocen ampliamente como "las ecuaciones de Briggs". Posteriormente, Briggs modificó sus ecuaciones de elevación de la pluma de 1969 en 1971 y 1972.

Briggs dividió las columnas de contaminación del aire en estas cuatro categorías generales:

• Plumas de chorro frío en condiciones de aire ambiente en calma
• Plumas de chorro frío en condiciones de aire ambiente ventoso
• Plumas calientes y flotantes en condiciones de aire ambiente en calma
• Plumas calientes y flotantes en condiciones de aire ambiente ventoso

Briggs consideró que la trayectoria de las plumas de los chorros fríos estaba dominada por su impulso de velocidad inicial, y la trayectoria de las plumas flotantes calientes estaba dominada por su impulso de flotación en la medida en que su impulso de velocidad inicial era relativamente poco importante. Aunque Briggs propuso ecuaciones de elevación de la pluma para cada una de las categorías de plumas anteriores, es importante enfatizar que "las ecuaciones de Briggs" que se utilizan ampliamente son las que propuso para plumas inclinadas y flotantes calientes.

En general, las ecuaciones de Briggs para penachos flotantes calientes inclinados se basan en observaciones y datos que involucran penachos de fuentes de combustión típicas, como las chimeneas de gases de combustión de calderas generadoras de vapor que queman combustibles fósiles en grandes centrales eléctricas. Por lo tanto, las velocidades de salida de la chimenea estaban probablemente en el rango de 20 a 100 pies/s (6 a 30 m/s) con temperaturas de salida que oscilaban entre 250 y 500 °F (120 a 260 °C).

A continuación se presenta un diagrama lógico para usar las ecuaciones de Briggs para obtener la trayectoria ascendente de la pluma de las plumas flotantes inclinadas:

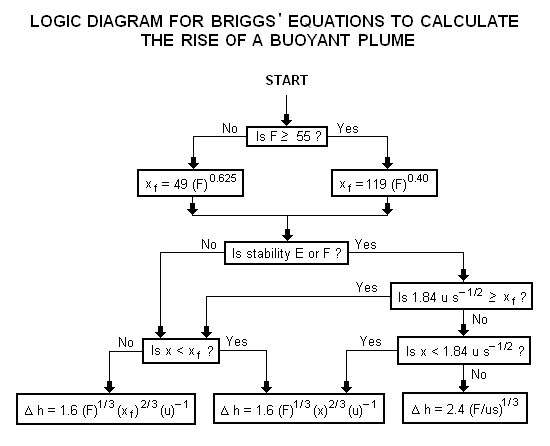
dónde:
Δh	= elevación de la pluma, en m
F	= factor de flotabilidad, en m s
X	= distancia a favor del viento desde la fuente de la pluma, en m
x f	= distancia a favor del viento desde la fuente del penacho hasta el punto de máxima elevación del penacho, en m
tu	= velocidad del viento a la altura real de la chimenea, en m/s
s	= parámetro de estabilidad, en s

Los parámetros anteriores utilizados en las ecuaciones de Briggs se analizan en el libro de Beychok.