Mínimos cuadrados

El resultado de la fijación de un conjunto de puntos de datos con una función cuadrática

Ajuste cónico un conjunto de puntos usando aproximación de mínimos cuadrados

El método de mínimos cuadrados es un enfoque estándar en el análisis de regresión para aproximar la solución de sistemas sobredeterminados (conjuntos de ecuaciones en los que hay más ecuaciones que incógnitas) al minimizar la suma de los cuadrados de los residuos (un residuo es la diferencia entre un valor observado y el valor ajustado provisto por un modelo) hechos en los resultados de cada ecuación individual.

La aplicación más importante es el ajuste de datos. Cuando el problema tiene incertidumbres sustanciales en la variable independiente (la variable x), entonces los métodos de regresión simple y de mínimos cuadrados tienen problemas; en tales casos, se puede considerar la metodología requerida para ajustar modelos de errores en variables en lugar de la de mínimos cuadrados.

Los problemas de mínimos cuadrados se dividen en dos categorías: mínimos cuadrados lineales u ordinarios y mínimos cuadrados no lineales, dependiendo de si los residuos son o no lineales en todas las incógnitas. El problema de los mínimos cuadrados lineales ocurre en el análisis de regresión estadística; tiene una solución de forma cerrada. El problema no lineal generalmente se resuelve mediante un refinamiento iterativo; en cada iteración, el sistema se aproxima a uno lineal y, por lo tanto, el cálculo central es similar en ambos casos.

Los mínimos cuadrados polinómicos describen la varianza en una predicción de la variable dependiente en función de la variable independiente y las desviaciones de la curva ajustada.

Cuando las observaciones provienen de una familia exponencial con identidad como su suficiente estadística natural y se cumplen condiciones leves (por ejemplo, para distribuciones normales, exponenciales, de Poisson y binomiales), las estimaciones de mínimos cuadrados estandarizados y las estimaciones de máxima verosimilitud son idénticas. El método de mínimos cuadrados también se puede derivar como un método de estimación de momentos.

La siguiente discusión se presenta principalmente en términos de funciones lineales, pero el uso de mínimos cuadrados es válido y práctico para familias de funciones más generales. Además, al aplicar iterativamente la aproximación cuadrática local a la probabilidad (a través de la información de Fisher), el método de mínimos cuadrados puede usarse para ajustar un modelo lineal generalizado.

El método de los mínimos cuadrados fue descubierto y publicado oficialmente por Adrien-Marie Legendre (1805), aunque por lo general también se atribuye a Carl Friedrich Gauss (1795), quien contribuyó con importantes avances teóricos al método y es posible que lo haya utilizado anteriormente. eso en su obra.

Historia

Fundación

El método de los mínimos cuadrados surgió de los campos de la astronomía y la geodesia, cuando científicos y matemáticos buscaban soluciones a los desafíos de navegar por los océanos de la Tierra durante la era de los descubrimientos. La descripción precisa del comportamiento de los cuerpos celestes fue la clave para permitir que los barcos navegaran en mar abierto, donde los marineros ya no podían depender de los avistamientos terrestres para navegar.

El método fue la culminación de varios avances que tuvieron lugar durante el transcurso del siglo XVIII:

• La combinación de diferentes observaciones como la mejor estimación del valor verdadero; los errores disminuyen con agregación en lugar de aumentar, tal vez primero expresado por Roger Cotes en 1722.
• La combinación de diferentes observaciones tomadas bajo la igual condiciones contrarias a simplemente probar lo mejor de uno para observar y grabar una sola observación con precisión. El enfoque era conocido como el método de promedios. Este enfoque fue utilizado notablemente por Tobias Mayer mientras estudiaba las libraciones de la luna en 1750, y por Pierre-Simon Laplace en su trabajo para explicar las diferencias en movimiento de Júpiter y Saturno en 1788.
• La combinación de las diferentes observaciones realizadas diferentes condiciones. El método llegó a ser conocido como el método menos la desviación absoluta. Fue realizado notablemente por Roger Joseph Boscovich en su trabajo sobre la forma de la tierra en 1757 y por Pierre-Simon Laplace para el mismo problema en 1799.
• El desarrollo de un criterio que se puede evaluar para determinar cuándo se ha logrado la solución con el error mínimo. Laplace intentó especificar una forma matemática de la densidad de probabilidad para los errores y definir un método de estimación que minimiza el error de estimación. Para ello, Laplace utilizó una distribución exponencial simétrica de dos caras que ahora llamamos distribución Laplace para modelar la distribución de errores, y usó la suma de desviación absoluta como error de estimación. Sentía que estas eran las suposiciones más simples que podía hacer, y esperaba obtener la media aritmética como la mejor estimación. En cambio, su estimador era la mediana posterior.

El método

Carl Friedrich Gauss

La primera exposición clara y concisa del método de los mínimos cuadrados fue publicada por Legendre en 1805. La técnica se describe como un procedimiento algebraico para ajustar ecuaciones lineales a datos y Legendre demuestra el nuevo método analizando los mismos datos que Laplace para la forma de la tierra. Diez años después de la publicación de Legendre, el método de los mínimos cuadrados se adoptó como herramienta estándar en astronomía y geodesia en Francia, Italia y Prusia, lo que constituye una aceptación extraordinariamente rápida de una técnica científica.

En 1809, Carl Friedrich Gauss publicó su método para calcular las órbitas de los cuerpos celestes. En ese trabajo afirmó haber estado en posesión del método de los mínimos cuadrados desde 1795. Esto, naturalmente, condujo a una disputa de prioridad con Legendre. Sin embargo, para crédito de Gauss, fue más allá de Legendre y logró conectar el método de los mínimos cuadrados con los principios de probabilidad y con la distribución normal. Logró completar el programa de Laplace de especificar una forma matemática de la densidad de probabilidad de las observaciones, dependiendo de un número finito de parámetros desconocidos, y definir un método de estimación que minimiza el error de estimación. Gauss demostró que la media aritmética es de hecho la mejor estimación del parámetro de ubicación cambiando tanto la densidad de probabilidad como el método de estimación. Luego le dio la vuelta al problema preguntando qué forma debería tener la densidad y qué método de estimación debería usarse para obtener la media aritmética como estimación del parámetro de ubicación. En este intento, inventó la distribución normal.

Una de las primeras demostraciones de la fuerza del método de Gauss se produjo cuando se utilizó para predecir la ubicación futura del asteroide Ceres recién descubierto. El 1 de enero de 1801, el astrónomo italiano Giuseppe Piazzi descubrió Ceres y pudo seguir su camino durante 40 días antes de que se perdiera en el resplandor del sol. Sobre la base de estos datos, los astrónomos deseaban determinar la ubicación de Ceres después de que emergiera por detrás del sol sin resolver las complicadas ecuaciones no lineales del movimiento planetario de Kepler. Las únicas predicciones que permitieron con éxito al astrónomo húngaro Franz Xaver von Zach reubicar a Ceres fueron las realizadas por Gauss, de 24 años, utilizando el análisis de mínimos cuadrados.

En 1810, después de leer el trabajo de Gauss, Laplace, después de demostrar el teorema del límite central, lo usó para dar una justificación de muestra grande para el método de los mínimos cuadrados y la distribución normal. En 1822, Gauss pudo afirmar que el enfoque de mínimos cuadrados para el análisis de regresión es óptimo en el sentido de que en un modelo lineal donde los errores tienen una media de cero, no están correlacionados y tienen varianzas iguales, el mejor estimador lineal insesgado de los coeficientes es el estimador de mínimos cuadrados. Este resultado se conoce como el teorema de Gauss-Markov.

La idea del análisis de mínimos cuadrados también fue formulada de forma independiente por el estadounidense Robert Adrian en 1808. En los siguientes dos siglos, los trabajadores de la teoría de los errores y de la estadística encontraron muchas formas diferentes de implementar los mínimos cuadrados.

Enunciado del problema

El objetivo consiste en ajustar los parámetros de una función modelo para adaptarse mejor a un conjunto de datos. Un conjunto de datos simple consiste en n puntos (pares de datos) ${displaystyle (x_{i},y_{i}!}$, i = 1,... n, donde ${displaystyle x_{i}!$ es una variable independiente y ${displaystyle ¡Sí!$ es una variable dependiente cuyo valor se encuentra por observación. La función modelo tiene la forma ${beta}}$, donde m parámetros ajustables se mantienen en el vector ${displaystyle {boldsymbol {beta }$. El objetivo es encontrar los valores del parámetro para el modelo que "mejor" se ajuste a los datos. El ajuste de un modelo a un punto de datos se mide por su residual, definido como la diferencia entre el valor observado de la variable dependiente y el valor predicho por el modelo:

${displaystyle r_{i}=y_{i}-f(x_{i},{boldsymbol {beta }}$

Los residuos se trazan contra los correspondientes ${displaystyle x}$ valores. Las fluctuaciones aleatorias sobre ${displaystyle R_{i}=0}$ indicar un modelo lineal es apropiado.

El método menos cuadrado encuentra los valores óptimos del parámetro minimizando la suma de residuos cuadrados, ${displaystyle S.$:

${displaystyle S=sum ¿Qué?$

En el caso más simple ${displaystyle f(x_{i},{boldsymbol {beta }=beta }$ y el resultado del método menos cuadrado es la media aritmética de los datos de entrada.

Un ejemplo de un modelo en dos dimensiones es el de la línea recta. Denotar el e-intercepto como ${displaystyle beta ¿Qué?$ y la pendiente como ${displaystyle beta ¿Qué?$, la función modelo es dada por ${beta}=beta ¿Qué?$. Vea los mínimos cuadrados lineales para un ejemplo completo de este modelo.

Un punto de datos puede constar de más de una variable independiente. Por ejemplo, al ajustar un plano a un conjunto de medidas de altura, el plano es una función de dos variables independientes, x y z, digamos. En el caso más general, puede haber una o más variables independientes y una o más variables dependientes en cada punto de datos.

A la derecha es un diagrama residual que ilustra las fluctuaciones aleatorias sobre ${displaystyle R_{i}=0}$, indicando que un modelo lineal${displaystyle (Y_{i}=alpha +beta x_{i}+U_{i}}$ es apropiado. ${displaystyle U_{i}$ es una variable independiente y aleatoria.

Los residuos se trazan contra el correspondiente ${displaystyle x}$ valores. La forma parabólica de las fluctuaciones sobre ${displaystyle R_{i}=0}$ indica que es apropiado un modelo parabólico.

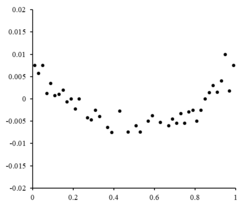
Si los puntos residuales tenían algún tipo de forma y no fluctuaban aleatoriamente, un modelo lineal no sería apropiado. Por ejemplo, si la trama residual tenía una forma parabólica como se ve a la derecha, un modelo parabólico ${displaystyle (Y_{i}=alpha +beta x_{i}+gamma #$ sería apropiado para los datos. Los residuos para un modelo parabólico se pueden calcular a través de ${displaystyle {fn}- {fn}- {beta}- {beta} }x_{i}-{widehat {gamma} }x_{i} {2}$.

Limitaciones

Esta formulación de regresión considera solo los errores de observación en la variable dependiente (pero la regresión alternativa de mínimos cuadrados totales puede tener en cuenta los errores en ambas variables). Hay dos contextos bastante diferentes con diferentes implicaciones:

• Regresión por predicción. Aquí se instala un modelo para proporcionar una regla de predicción para la aplicación en una situación similar a la que se aplican los datos utilizados para la fijación. Aquí las variables dependientes correspondientes a dicha aplicación futura estarían sujetas a los mismos tipos de error de observación que los de los datos utilizados para el ajuste. Por lo tanto, es lógicamente consistente en utilizar la norma de predicción de menor escala para esos datos.
• Regreso para encajar una "relación verdadera". En el análisis estándar de regresión que conduce a la fijación por mínimos cuadrados hay una hipótesis implícita de que los errores en la variable independiente son cero o estrictamente controlados para ser insignificantes. Cuando los errores en la variable independiente no son insignificantes, se pueden utilizar modelos de error de medición; estos métodos pueden llevar a estimaciones de parámetros, pruebas de hipótesis y intervalos de confianza que tienen en cuenta la presencia de errores de observación en las variables independientes. Un enfoque alternativo es ajustarse a un modelo por un total de mínimos cuadrados; esto se puede considerar como adoptar un enfoque pragmático para equilibrar los efectos de las diferentes fuentes de error en la formulación de una función objetiva para el uso en el ajuste de modelos.

Resolviendo el problema de los mínimos cuadrados

El mínimo de la suma de los cuadrados se encuentra al establecer el gradiente en cero. Dado que el modelo contiene parámetros m, existen ecuaciones de gradiente m:

$${fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {fnMicrosoft {\fnMicrosoft} S}{partial beta - ¿Qué? ¿Por qué? {beta} {beta parcial} {beta}}}} {fnMicrosoft}}}}}} {beta parcial}}} {beta parcial}}}}}}} {beta parcial ¿Qué?$$

${displaystyle.$

$${displaystyle -2sum _{i}r_{i}{frac {partial f(x_{i},{boldsymbol {beta }}}}{partial beta - Sí.$$

Las ecuaciones de gradiente se aplican a todos los problemas de mínimos cuadrados. Cada problema particular requiere expresiones particulares para el modelo y sus derivadas parciales.

Mínimos cuadrados lineales

Un modelo de regresión es lineal cuando el modelo comprende una combinación lineal de los parámetros, es decir,

$${displaystyle f(x,{boldsymbol {beta }}=sum _{j=1}beta _{j}phi _{j}(x),}$$

${displaystyle phi _{j}$

${displaystyle x}$

Letting ${displaystyle X_{ij}=phi _{j}(x_{i})}$ y poner las variables independientes y dependientes en matrices ${displaystyle X}$ y ${displaystyle Sí.$, respectivamente, podemos calcular los mínimos cuadrados de la siguiente manera. Note que ${displaystyle D}$ es el conjunto de todos los datos.

$${fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {bet}} {fnMicrosoft Sans} {fnMicrosoft Sans Serif} {fnMicrosoft} {fnMicrosoft} {fnMicrosoft} }-{boldsymbol {beta } {Mathsf {}X^{mathsf Y+{boldsymbol {beta} } {Mathsf {}X^{mathsf #X{boldsymbol {beta} }$$

El gradiente de la pérdida es:

$${fnMicroc {fnMicrosoft Sans Serif} {fnMicrosoft Sans Serif} {beta}}} {boldsymbol {beta {fnMicroc {cHFF}X{boldsymbol {betam} }-{boldsymbol {beta } {Mathsf {}X^{mathsf Y+{boldsymbol {beta} ################################################################################################################################################################################################################################################################ - Sí. }$$

Establecer el gradiente de la pérdida a cero y resolver para ${displaystyle {boldsymbol {beta }$, tenemos:

$${displaystyle -2X^{mathsf {T}}Y+2X^{mathsf {T}X{boldsymbol {beta }=0Rightarrow X^{mathsf {T}Y=X^{mathsf {T}X{boldsymbol {beta }$$

$${displaystyle {boldsymbol {hat {beta }=left(X^{mathsf {T}Xright)^{-1}X^{mathsf {T}Y}$$

Mínimos cuadrados no lineales

Hay, en algunos casos, una solución de forma cerrada a un problema de mínimos cuadrados no lineales – pero en general no existe. En caso de no solución de forma cerrada, se utilizan algoritmos numéricos para encontrar el valor de los parámetros ${displaystyle beta }$ que minimiza el objetivo. La mayoría de los algoritmos implican elegir valores iniciales para los parámetros. Luego, los parámetros son refinados iterativamente, es decir, los valores se obtienen por aproximación sucesiva:

$${beta} {beta} {fnK}}= {beta} ¿Qué? Delta beta _{j},}$$

${displaystyle Delta beta _{j}}$

${displaystyle {boldsymbol {beta } {k}$

$${displaystyle {begin{aligned}f(x_{i},{boldsymbol {beta })}=f^{k}(x_{i},{boldsym {bolbeta })+sum _{j}{frac {partial f(x_{i},{boldsymbol {beta })}}{betabeta}}}}}left(beta)} {beta}}}} {beta {beta}}}}}}}}}beta}}}}beta {beta {beta {beta}}}}}}}}beta}}}}}}}}}}}}}}}}}}}}}}}}beta}}}}}betam}}}}beta {beta {beta {beta {beta {beta {beta {betam}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} ¿Qué? ¿Qué? {beta})+sum _{j}J_{ij},Delta beta ¿Qué?$$

La J jacobiana es una función de constantes, la variable independiente y los parámetros, por lo que cambia de una iteración a la siguiente. Los residuos están dados por

$${displaystyle ¿Qué? {beta}})-sum "Delta beta" ¿Qué? Delta Y... "Delta beta" _{j}.$$

Para minimizar la suma de cuadrados ${displaystyle R_{i}$, la ecuación gradiente se establece a cero y resuelto para ${displaystyle Delta beta _{j}}$:

$${displaystyle -2sum - ¿Por qué? Y... "Delta beta"$$

$${displaystyle sum - ¿Qué? #### {k=1} {m}J_{ij}J_{ik}Delta beta ¿Qué? ¿Por qué? Delta y. }$$

Las ecuaciones normales se escriben en notación matricial como

$${displaystyle left(mathbf {J} ^{mathsf {T}Mathbf {J} right) Delta {boldsymbol {beta Delta mathbf {y}$$

Estas son las ecuaciones definitorias del algoritmo de Gauss-Newton.

Diferencias entre mínimos cuadrados lineales y no lineales

• La función modelo, f, en LLSQ (línea menos cuadrados) es una combinación lineal de parámetros de la forma ${displaystyle f=X_{i1}beta ¿Qué? ¿Qué?$ El modelo puede representar una línea recta, una parabola o cualquier otra combinación lineal de funciones. En NLLSQ (no linear menos cuadrados) los parámetros aparecen como funciones, tales como ${displaystyle beta ^{2},e^{beta x}$ y así sucesivamente. Si los derivados ${displaystyle partial f/partial beta _{j}$ son constantes o dependen sólo de los valores de la variable independiente, el modelo es lineal en los parámetros. De lo contrario el modelo no es lineal.
• Necesita valores iniciales para los parámetros para encontrar la solución a un problema NLLSQ; LLSQ no los requiere.
• Los algoritmos de solución para NLLSQ a menudo requieren que el Jacobian puede ser calculado similar a LLSQ. Las expresiones analíticas para los derivados parciales pueden ser complicadas. Si las expresiones analíticas son imposibles de obtener o los derivados parciales deben ser calculadas por aproximación numérica o una estimación debe hacerse del jacobino, a menudo a través de diferencias finitas.
• La no convergencia (falificación del algoritmo para encontrar un mínimo) es un fenómeno común en NLLSQ.
• LLSQ es globalmente concave por lo que la no convergencia no es un problema.
• Solver NLLSQ es generalmente un proceso iterativo que tiene que ser terminado cuando un criterio de convergencia está satisfecho. Las soluciones LLSQ se pueden calcular utilizando métodos directos, aunque los problemas con un gran número de parámetros se resuelven típicamente con métodos iterativos, como el método Gauss-Seidel.
• En LLSQ la solución es única, pero en NLLSQ puede haber múltiples minima en la suma de cuadrados.
• Bajo la condición de que los errores no estén relacionados con las variables predictoras, LLSQ produce estimaciones imparciales, pero incluso bajo esa condición las estimaciones NLLSQ son generalmente parciales.

Estas diferencias deben tenerse en cuenta siempre que se busque la solución a un problema de mínimos cuadrados no lineales.

Ejemplo

Considere un ejemplo simple extraído de la física. Un resorte debe obedecer la ley de Hooke, que establece que la extensión de un resorte y es proporcional a la fuerza, F, aplicado a él.

${displaystyle y=f(F,k)=kF!}$

constituye el modelo, donde F es la variable independiente. Para estimar la constante de la fuerza, k, realizamos una serie de n mediciones con diferentes fuerzas para producir un conjunto de datos, ${displaystyle (F_{i}, i=1,dotsn}$, donde Sí._i es una extensión de primavera medida. Cada observación experimental contendrá algún error, ${displaystyle varepsilon }$, y así podemos especificar un modelo empírico para nuestras observaciones,

${displaystyle Y....$

Hay muchos métodos que podríamos usar para estimar el parámetro desconocido k. Dado que las ecuaciones n en las variables m de nuestros datos comprenden un sistema sobredeterminado con una incógnita y ecuaciones n, estimamos k utilizando mínimos cuadrados. La suma de cuadrados a minimizar es

${displaystyle S=sum ¿Qué?$

La estimación de mínimos cuadrados de la constante de fuerza, k, está dada por

${displaystyle {hat {fnK}={frac {fnMicroc} {fnK}}= {fn}fnK}} {f}fnK}fnK}} {fnK}}f}}fnfnf}fnKfnKf}fnKfnKf}}}f}}}}}}f}}}fnfnfnfnfnKfnfnfnf}fnfnfnKfnKfnKf}fnf}fnfnKfnKfnKfnKfnKfnKfnfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKfnKf}}}}fn ¿Por qué? - Sí.$

Suponemos que la aplicación de fuerza hace que el resorte se expanda. Después de haber derivado la constante de fuerza por ajuste de mínimos cuadrados, predecimos la extensión a partir de la ley de Hooke.

Cuantificación de la incertidumbre

En un cálculo mínimo de cuadrados con pesos unitarios, o en regresión lineal, la varianza en la jt parámetro, denotado ${displaystyle operatorname {var} ({hat {beta - Sí.$, generalmente se calcula con

${displaystyle operatorname {var} ({hat {beta - Sí. ^{2}left [X^{mathsf {T}Xright]^{-1}right)_{j}approx {fnfn sigma} } {2}C_{j},}$

${displaystyle {hat {sigma}. {fnMicroc {S} {n-m}}$

${displaystyle C=left(X^{mathsf {T}Xright)}{-1}$

donde la varianza del error verdadero σ² se reemplaza por una estimación, el estadístico chi-cuadrado reducido, basado en el valor minimizado de la suma residual de los cuadrados (objetivo función), S. El denominador, n − m, son los grados de libertad estadísticos; ver grados efectivos de libertad para generalizaciones. C es la matriz de covarianza.

Pruebas estadísticas

Si se conoce la distribución de probabilidad de los parámetros o se realiza una aproximación asintótica, se pueden encontrar los límites de confianza. De manera similar, se pueden realizar pruebas estadísticas sobre los residuos si se conoce o supone la distribución de probabilidad de los residuos. Podemos derivar la distribución de probabilidad de cualquier combinación lineal de las variables dependientes si se conoce o asume la distribución de probabilidad de los errores experimentales. Inferir es fácil cuando se supone que los errores siguen una distribución normal, lo que implica que las estimaciones de los parámetros y los residuos también se distribuirán normalmente condicionados a los valores de las variables independientes.

Es necesario hacer suposiciones sobre la naturaleza de los errores experimentales para probar los resultados estadísticamente. Una suposición común es que los errores pertenecen a una distribución normal. El teorema del límite central apoya la idea de que esta es una buena aproximación en muchos casos.

• El teorema Gauss-Markov. En un modelo lineal en el que los errores tienen expectativa cero condicional sobre las variables independientes, son incorrelacionados y tienen diferencias iguales, el mejor estimador lineal sin prejuicios de cualquier combinación lineal de las observaciones, es su estimador de menos cuadras. "Mejor" significa que los estimadores menos cuadrados de los parámetros tienen una varianza mínima. La hipótesis de la misma varianza es válida cuando todos los errores pertenecen a la misma distribución.
• Si los errores pertenecen a una distribución normal, los estimadores de menos cuadras son también los estimadores de mayor probabilidad en un modelo lineal.

Sin embargo, suponga que los errores no se distribuyen normalmente. En ese caso, un teorema del límite central a menudo implica, sin embargo, que las estimaciones de los parámetros se distribuirán de manera aproximadamente normal siempre que la muestra sea razonablemente grande. Por esta razón, dada la importante propiedad de que la media del error es independiente de las variables independientes, la distribución del término de error no es un tema importante en el análisis de regresión. Específicamente, normalmente no es importante si el término de error sigue una distribución normal.

Mínimos cuadrados ponderados

"Fanning Out" Efecto de Heteroscedasticidad

Un caso especial de plazas menos generalizadas llamadas peso menos cuadrados ocurre cuando todas las entradas fuera de la diagonal Ω (la matriz de correlación de los residuales) son nulas; las diferencias de las observaciones (junto con la matriz de covariancia diagonal) pueden todavía ser desiguales (heteroscedasticidad). En términos más simples, la heteroscedasticidad es cuando la varianza ${displaystyle Y...$ depende del valor ${displaystyle x_{i}}$ que hace que la trama residual crea un efecto "fanning out" hacia mayor ${displaystyle Y...$ valores vistos en la parcela residual a la derecha. Por otro lado, la homoscedasticidad está suponiendo que la varianza ${displaystyle Y...$ y diferencia de ${displaystyle U_{i}$ son iguales.

Relación con los componentes principales

El primer componente principal sobre la media de un conjunto de puntos puede ser representado por esa línea que se acerca más de cerca a los puntos de datos (como medida por distancia cuadrada del enfoque más cercano, es decir perpendicular a la línea). En contraste, los mínimos cuadrados lineales intentan minimizar la distancia en la ${displaystyle y}$ sólo dirección. Por lo tanto, aunque los dos utilizan un error métrico similar, los cuadrados menos lineales es un método que trata una dimensión de los datos preferencialmente, mientras que PCA trata todas las dimensiones por igual.

Relación con la teoría de la medida

La notable estadística Sara van de Geer usó la teoría de procesos empíricos y la dimensión de Vapnik-Chervonenkis para demostrar que un estimador de mínimos cuadrados puede interpretarse como una medida en el espacio de funciones integrables al cuadrado.

Regularización

Regularización de Tikhonov

En algunos contextos puede ser preferible una versión regularizada de la solución menos cuadrada. La regularización de Tikhonov (o regresión de la cresta) añade una limitación que ${displaystylefnbeta {2}}$, el cuadrado ${displaystyle ell _{2}$-norm del vector del parámetro, no es mayor que un valor dado a la formulación de los mínimos cuadrados, lo que conduce a un problema de minimización limitado. Esto equivale al problema de minimización sin restricciones en el que la función objetiva es la suma residual de plazas más un plazo de penalización ${displaystyle alphabeta {2}}$ y ${displaystyle alpha }$ es un parámetro de ajuste (esta es la forma lagrangiana del problema de minimización limitada).

En un contexto bayesiano, esto es equivalente a colocar una media cero normalmente distribuida antes en el vector de parámetros.

Método del lazo

Una versión regularizada alternativa de los mínimos cuadrados es Lasso (al menos la contracción absoluta y el operador de selección), que utiliza la limitación que ${displaystylefnbeta {}}$, el L1-norm del vector del parámetro, no es mayor que un valor dado. (Uno puede mostrar como arriba usando multiplicadores de Lagrange que esto es equivalente a una minimización sin restricciones de la pena de menos cuadras con ${displaystyle alphabeta {}}$ añadido.) En un contexto bayesiano, esto equivale a colocar una distribución previa de cero medios en el vector del parámetro. El problema de optimización puede resolverse utilizando métodos de programación cuadrática o de optimización de convexos más generales, así como algoritmos específicos como el algoritmo de regresión de ángulo mínimo.

Una de las principales diferencias entre Lasso y la regresión de las crestas es que en la regresión de las crestas, a medida que se aumenta la pena, todos los parámetros se reducen mientras que todavía quedan no cero, mientras que en Lasso, aumentar la pena causará que cada vez más de los parámetros se conduzcan a cero. Esta es una ventaja de la regresión de las crestas, ya que los parámetros de conducción a cero deseleccionan las características de la regresión. Por lo tanto, Lasso selecciona automáticamente características más relevantes y descarta a los demás, mientras que la regresión Ridge nunca descarta completamente ninguna característica. Algunas técnicas de selección de características se desarrollan sobre la base de LASSO incluyendo Bolasso que muestra bootstraps, y FeaLect que analiza los coeficientes de regresión correspondientes a diferentes valores de ${displaystyle alpha }$ para marcar todas las características.

La formulación L¹-regularizada es útil en algunos contextos debido a su tendencia a preferir soluciones donde más parámetros son cero, lo que da soluciones que dependen de menos variables. Por esta razón, el Lasso y sus variantes son fundamentales en el campo de la detección comprimida. Una extensión de este enfoque es la regularización neta elástica.