Métodos para calcular raíces cuadradas

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Algoritmos para calcular las raíces cuadradas

Métodos de cálculo de raíces cuadradas son algoritmos para aproximar la raíz cuadrada no negativa ${displaystyle {sqrt {S}}}$ de un número real positivo ${displaystyle S}$ . Puesto que todas las raíces cuadradas de los números naturales, aparte de los cuadrados perfectos, son irracionales, Las raíces cuadradas solo pueden ser calculadas a cierta precisión finita: estos métodos suelen construir una serie de aproximaciones cada vez más precisas.

La mayoría de los métodos de cálculo de raíz cuadrada son iterativos: después de elegir una estimación inicial adecuada ${displaystyle {sqrt {S}}}$ , un refinamiento iterativo se realiza hasta que se cumpla algún criterio de terminación. Un esquema de refinamiento es el método de Heron, un caso especial del método de Newton. Si la división es mucho más costosa que la multiplicación, puede ser preferible calcular la raíz cuadrada inversa en su lugar.

Hay otros métodos disponibles para calcular la raíz cuadrada dígito por dígito, o usando series de Taylor. Las aproximaciones racionales de raíces cuadradas se pueden calcular utilizando expansiones de fracciones continuas.

El método empleado depende de la precisión necesaria y de las herramientas y la potencia computacional disponibles. Los métodos pueden clasificarse a grandes rasgos como aquellos adecuados para el cálculo mental, aquellos que normalmente requieren al menos papel y lápiz, y aquellos que se implementan como programas para ejecutarse en una computadora electrónica digital u otro dispositivo informático. Los algoritmos pueden tener en cuenta la convergencia (cuántas iteraciones se requieren para lograr una precisión específica), la complejidad computacional de operaciones individuales (es decir, división) o iteraciones y la propagación de errores (la precisión del resultado final).

Algunos métodos, como la división sintética con lápiz y papel y la expansión de series, no requieren un valor inicial. En algunas aplicaciones, se requiere una raíz cuadrada entera, que es la raíz cuadrada redondeada o truncada al entero más cercano (en este caso se puede emplear un procedimiento modificado).

Historia

Los procedimientos para encontrar raíces cuadradas (particularmente la raíz cuadrada de 2) se conocen al menos desde el período de la antigua Babilonia en el siglo XVII a.C. Los matemáticos babilónicos calcularon la raíz cuadrada de 2 a tres "dígitos" sexagesimales. después del 1, pero no se sabe exactamente cómo. Sabían cómo aproximar una hipotenusa usando

{displaystyle {sqrt {a^{2}+b^{2}}}approx a+{frac {1}{2}}b^{2}a^{-1}}

{displaystyle {frac {41}{60}}+{frac {15}{3600}}}

{displaystyle {frac {40}{60}}}

{displaystyle {frac {10}{60}}}

{displaystyle {sqrt {2}}.}

Método de Heron desde el primer siglo Egipto fue el primer algoritmo verificable para computar la raíz cuadrada.

Los métodos analíticos modernos comenzaron a desarrollarse después de la introducción del sistema de numeración arábiga en Europa occidental a principios del Renacimiento.

Hoy en día, casi todos los dispositivos informáticos tienen una función de raíz cuadrada rápida y precisa, ya sea como una construcción de lenguaje de programación, una función intrínseca del compilador o de biblioteca, o como un operador de hardware, basado en uno de los procedimientos descritos.

Estimación inicial

Muchos algoritmos de raíz cuadrada iterativa requieren un valor inicial de semilla. La semilla debe ser un número no cero positivo; debe ser entre 1 y ${displaystyle S}$ , el número cuya raíz cuadrada es deseada, porque la raíz cuadrada debe estar en ese rango. Si la semilla está lejos de la raíz, el algoritmo requerirá más iteraciones. Si uno inicializa con ${displaystyle x_{0}=1}$ (o ${displaystyle S}$ ), entonces aproximadamente ${displaystyle {tfrac {1}{2}}vert log _{2}Svert }$ las iteraciones se desperdiciarán sólo conseguir el orden de magnitud de la raíz. Por lo tanto, es útil tener una estimación aproximada, que puede tener una precisión limitada pero es fácil de calcular. En general, cuanto mejor sea la estimación inicial, más rápido será la convergencia. Para el método de Newton (también llamado método de Babylonian o Heron), una semilla algo más grande que la raíz convergerá ligeramente más rápido que una semilla algo más pequeña que la raíz.

En general, una estimación se ajusta a un intervalo arbitrario conocido para contener la raíz (como ${displaystyle [x_{0},S/x_{0}]}$ ). La estimación es un valor específico de una aproximación funcional a ${displaystyle f(x)={sqrt {x}}}$ sobre el intervalo. Obtener una mejor estimación implica obtener límites más ajustados en el intervalo, o encontrar una mejor aproximación funcional a ${displaystyle f(x)}$ . Este último normalmente significa utilizar un polinomio de orden superior en la aproximación, aunque no todas las aproximaciones son polinomio. Los métodos comunes de estimación incluyen escalar, linear, hiperbólico y logarítmico. Una base decimal se utiliza generalmente para la estimación mental o de papel y lápiz. Una base binaria es más adecuada para las estimaciones del ordenador. Al estimar, el exponente y la mantissa se tratan generalmente por separado, ya que el número se expresaría en la notación científica.

Estimaciones decimales

Típicamente el número ${displaystyle S}$ se expresa en la notación científica como ${displaystyle atimes 10^{2n}}$ Donde $<math alttext="{displaystyle 1leq a1\leq \leq ac)100{displaystyle 1leq a realizadas100} <img alt="{displaystyle 1leq a$ y n es un entero, y la gama de posibles raíces cuadradas es ${displaystyle {sqrt {a}}times 10^{n}}$ Donde $<math alttext="{displaystyle 1leq {sqrt {a}}1\leq \leq ac)10{displaystyle 1leq {sqrt {a} {fn} <img alt="{displaystyle 1leq {sqrt {a}}$ .

Estimaciones de escalas

Los métodos de escalar dividen el rango en intervalos, y la estimación en cada intervalo está representada por un solo número de escalar. Si el rango es considerado como un solo intervalo, la media aritmética (5.5) o media geométrica ( ${displaystyle {sqrt {10}}approx 3.16}$ ) veces ${displaystyle 10^{n}}$ son estimaciones plausibles. El error absoluto y relativo de éstos difiere. En general, un solo escalar será muy inexacto. Mejores estimaciones dividen el rango en dos o más intervalos, pero las estimaciones de escalar tienen una precisión inherentemente baja.

Para dos intervalos, divididos geométricamente, la raíz cuadrada ${displaystyle {sqrt {S}}={sqrt {a}}times 10^{n}}$ se puede estimar como

<math alttext="{displaystyle {sqrt {S}}approx {begin{cases}2cdot 10^{n}&{text{if }}aS. . {}2⋅ ⋅ 10nsi ac)10,6⋅ ⋅ 10nsi a≥ ≥ 10.{fnMicrosoft Sans Serif} {begin{cases}2cdot 10^{n} {text{if}a seccionó10,6cdot 10^{n} {text{if }agq 10.end{cases}}}}}}}}<img alt="{displaystyle {sqrt {S}}approx {begin{cases}2cdot 10^{n}&{text{if }}a

Esta estimación tiene el máximo error absoluto ${displaystyle 4cdot 10^{n}}$ a = 100, y error relativo máximo de 100% a = 1.

Por ejemplo, ${displaystyle S=125348}$ factor considerado ${displaystyle 12.5348times 10^{4}}$ , la estimación es ${displaystyle {sqrt {S}}approx 6cdot 10^{2}=600}$ . ${displaystyle {sqrt {125348}}=354.0}$ , un error absoluto de 246 y error relativo de casi 70%.

Estimaciones lineales

Una estimación mejor, y el método estándar utilizado, es una aproximación lineal a la función ${displaystyle y=x^{2}}$ sobre un pequeño arco. Si, como antecede, los poderes de la base se consideran fuera del número ${displaystyle S}$ y el intervalo reducido a ${displaystyle [1,100]}$ , una línea de secant que abarca el arco, o una línea tangente en algún lugar a lo largo del arco puede ser utilizado como la aproximación, pero una línea de regresión menos cuadrada que intersecte el arco será más precisa.

Una línea de regresión menos cuadrada minimiza la diferencia media entre la estimación y el valor de la función. Su ecuación es ${displaystyle y=8.7x-10}$ . Reordenando, ${displaystyle x=0.115y+1.15}$ . Redondear los coeficientes para facilitar el cálculo,

{displaystyle {sqrt {S}}approx (a/10+1.2)cdot 10^{n}}

Esa es la mejor estimación promedio que se puede lograr con una sola pieza aproximación lineal de la función y=x² en el intervalo ${displaystyle [1,100]}$ . Tiene un error absoluto máximo de 1.2 a=100 y un error relativo máximo de 30% a S=1 y 10.

Para dividir en 10, reste uno del exponente ${displaystyle a}$ , o figurativamente mover el punto decimal un dígito a la izquierda. Para esta formulación, cualquier constante aditiva 1 más un pequeño aumento hará una estimación satisfactoria para recordar el número exacto no es una carga. La aproximación (redondeada o no) utilizando una sola línea que abarca el rango ${displaystyle [1,100]}$ es menos de un dígito significativo de precisión; el error relativo es mayor de 1/2², por lo que se proporcionan menos de 2 bits de información. La precisión es severamente limitada porque el rango es dos órdenes de magnitud, bastante grande para este tipo de estimación.

Una estimación mucho mejor se puede obtener por una aproximación lineal de un lado: múltiples segmentos de líneas, cada uno aproximando un subarco del original. Cuantos más segmentos se utilizan, mejor es la aproximación. La forma más común es utilizar líneas tangentes; las opciones críticas son cómo dividir el arco y dónde colocar los puntos tangentes. Una manera eficaz de dividir el arco de Sí. = 1 a Sí. = 100 es geométricamente: para dos intervalos, los límites de los intervalos son la raíz cuadrada de los límites del intervalo original, 1×100, es decir. [1,²√100] y [²√100100. Para tres intervalos, los límites son las raíces del cubo de 100: [1,³√100]³√100,(³√100)²], y [³√100)²,100], etc. Para dos intervalos, ²√100 = 10, un número muy conveniente. Las líneas tangentes son fáciles de derivar, y se encuentran en x = √1*√10 y x = √10*√10. Sus ecuaciones son: ${displaystyle y=3.56x-3.16}$ y ${displaystyle y=11.2x-31.6}$ . Inversión, las raíces cuadradas son: ${displaystyle x=0.28y+0.89}$ y ${displaystyle x=.089y+2.8}$ . Así pues, ${displaystyle S=acdot 10^{2n}}$ :

<math alttext="{displaystyle {sqrt {S}}approx {begin{cases}(0.28a+0.89)cdot 10^{n}&{text{if }}aS. . {}()0,28a+0.89)⋅ ⋅ 10nsi ac)10,().089a+2.8)⋅ ⋅ 10nsi a≥ ≥ 10.{fnMicrosoft Sans Serif} {begin{cases}(0.28a+0.89)cdot 10^{n} {text{if}a {if }a 10,(.089a+2.8)cdot 10^{n} limit {if}agq 10.end{case}}}} {f}}}}}f}<img alt="{displaystyle {sqrt {S}}approx {begin{cases}(0.28a+0.89)cdot 10^{n}&{text{if }}a

Los errores absolutos máximos ocurren en los puntos altos de los intervalos, en a=10 y 100, y son 0,54 y 1,7 respectivamente. Los errores relativos máximos están en los puntos finales de los intervalos, a a=1, 10 y 100, y son 17% en ambos casos. 17% o 0.17 es mayor que 1/10, por lo que el método produce menos que un dígito decimal de precisión.

Estimaciones hiperbólicas

En algunos casos, las estimaciones hiperbólicas pueden ser eficaces, ya que una hiperbola es también una curva convexa y puede estar a lo largo de un arco de Y = x² mejor que una línea. Las estimaciones hiperbólicas son más computacionalmente complejas, porque necesariamente requieren una división flotante. Una aproximación hiperbólica casi óptima a x² en el intervalo ${displaystyle [1,100]}$ es y=190/(10-x)-20. Transpuesto, la raíz cuadrada es x = -190/(y+20)+10. Así pues, ${displaystyle S=acdot 10^{2n}}$ :

{displaystyle {sqrt {S}}approx left({frac {-190}{a+20}}+10right)cdot 10^{n}}

La división flotante debe tener una precisión de solo un dígito decimal, porque la estimación general es solo esa precisión y se puede hacer mentalmente. Una estimación hiperbólica es mejor en promedio que una estimación escalar o lineal. Tiene un error absoluto máximo de 1,58 en 100 y un error relativo máximo de 16,0% en 10. Para el peor caso en a=10, la estimación es 3,67. Si se comienza con 10 y se aplican las iteraciones de Newton-Raphson de inmediato, se necesitarán dos iteraciones, lo que arrojará 3,66, antes de que se supere la precisión de la estimación hiperbólica. Para un caso más típico como 75, la estimación hiperbólica es 8,00 y se necesitarían 5 iteraciones de Newton-Raphson comenzando en 75 para obtener un resultado más preciso.

Estimaciones aritméticas

Un método análogo a la aproximación lineal por partes pero que utiliza sólo ecuaciones aritméticas en lugar de algebraicas, utiliza las tablas de multiplicar a la inversa: la raíz cuadrada de un número entre 1 y 100 está entre 1 y 10, por lo que si sabemos que 25 es un cuadrado perfecto (5 × 5), y 36 es un cuadrado perfecto (6 × 6), entonces la raíz cuadrada de un número mayor o igual a 25 pero menor que 36, comienza con un 5. Lo mismo ocurre con los números entre otros cuadrados . Este método producirá un primer dígito correcto, pero no es exacto a un dígito: el primer dígito de la raíz cuadrada de 35, por ejemplo, es 5, pero la raíz cuadrada de 35 es casi 6.

Una mejor manera es dividir el rango en intervalos a mitad de camino entre los cuadrados. Entonces, cualquier número entre 25 y la mitad de 36, que es 30,5, estima 5; cualquier número mayor que 30,5 hasta 36, estima 6. El procedimiento solo requiere un poco de aritmética para encontrar un número límite en medio de dos productos de la tabla de multiplicar. Aquí hay una tabla de referencia de esos límites:

$a$	plaza más cercana	${displaystyle k={sqrt {a}}}$ Est.
1 a 2,5	1 (= 1²)	1
2.5 a 6.5	4 (= 2²)	2
6,5 a 12,5	9 (= 3²)	3
12,5 a 20,5	16 (= 4²)	4
20,5 a 30,5	25 (= 5²)	5
30,5 a 42,5	36 (= 6²)	6
42,5 a 56,5	49 (= 7²)	7
56,5 a 72,5	64 (= 8²)	8
72,5 a 90,5	81 (= 9²)	9
90,5 a 100	100 (= 10²)	10

La operación final es multiplicar la estimación $k$ por el poder de diez divididos por 2, así para ${displaystyle S=acdot 10^{2n}}$ ,

{displaystyle {sqrt {S}}approx kcdot 10^{n}}

El método produce implícitamente un dígito significativo de precisión, ya que redondea al mejor primer dígito.

El método puede ser extendido 3 dígitos significativos en la mayoría de los casos, interpolando entre las plazas más cercanas que atan el operand. Si $<math alttext="{displaystyle k^{2}leq ak2≤ ≤ ac)()k+1)2{displaystyle k^{2}leq a won(k+1)}<img alt="{displaystyle k^{2}leq a$ Entonces ${displaystyle {sqrt {a}}}$ es aproximadamente k más una fracción, la diferencia entre $a$ y k² dividido por la diferencia entre los dos cuadrados:

{displaystyle {sqrt {a}}approx k+R}

{displaystyle R={frac {(a-k^{2})}{(k+1)^{2}-k^{2}}}}

La operación final, como arriba, es multiplicar el resultado por la potencia de diez dividido por 2;

{displaystyle {sqrt {S}}={sqrt {a}}cdot 10^{n}approx (k+R)cdot 10^{n}}

$k$ es un dígito decimal y $R$ es una fracción que debe convertirse a decimal. Por lo general, tiene un solo dígito en el numerador y uno o dos dígitos en el denominador, por lo que la conversión a decimal se puede realizar mentalmente.

Ejemplo: halla la raíz cuadrada de 75. $75 = 75 \times 10 2 \cdot 0$ , entonces $a$ es 75 y $n$ es 0. De las tablas de multiplicar, la raíz cuadrada de la mantisa debe ser 8 punto algo porque 8 × 8 es 64, pero 9 × 9 es 81, demasiado grande, así que $k$ es 8; algo es la representación decimal de $R$ . La fracción $R$ es 75 - k² = 11, el numerador , y 81 - k² = 17, el denominador. 17/11 es un poco menos que 18/12, que es 2/3 o 0,67, así que adivina 0,66 (aquí está bien adivinar, el error es muy pequeño). Entonces la estimación es $8 +.66 = 8.66$ . √75 a tres dígitos significativos es 8,66, por lo que la estimación es buena a 3 dígitos significativos. No todas las estimaciones que utilicen este método serán tan precisas, pero sí cercanas.

Estimaciones binarias

Al trabajar en el sistema de numeral binario (como las computadoras hacen internamente), expresando ${displaystyle S}$ como ${displaystyle atimes 2^{2n}}$ Donde $<math alttext="{displaystyle 0.1_{2}leq a0.12≤ ≤ ac)102{displaystyle 0.1_{2}leq a won10_{2}<img alt="{displaystyle 0.1_{2}leq a$ , la raíz cuadrada ${displaystyle {sqrt {S}}={sqrt {a}}times 2^{n}}$ se puede estimar como

{displaystyle {sqrt {S}}approx (0.485+0.485cdot a)cdot 2^{n}}

que es la línea de regresión menos cuadrada a 3 coeficientes de dígitos significativos. ${displaystyle {sqrt {a}}}$ tiene el máximo error absoluto de 0.0408 a ${displaystyle a}$ =2, y error relativo máximo de 3.0% a ${displaystyle a}$ =1. Una estimación redondeada convenientemente conveniente (porque los coeficientes son poderes de 2) es:

{displaystyle {sqrt {S}}approx (0.5+0.5cdot a)cdot 2^{n}}

que tiene un error absoluto máximo de 0,086 en 2 y un error relativo máximo de 6,1 % en $a = 0,5$ y $a = 2,0$ .

Para ${displaystyle S=125348=1;1110;1001;1010;0100_{2}=1.1110;1001;1010;0100_{2}times 2^{16},}$ , la aproximación binaria da ${displaystyle {sqrt {S}}approx (0.5+0.5cdot a)cdot 2^{8}=1.0111;0100;1101;0010_{2}cdot 1;0000;0000_{2}=1.456cdot 256=372.8}$ . ${displaystyle {sqrt {125348}}=354.0}$ , por lo que la estimación tiene un error absoluto de 19 y un error relativo de 5.3%. El error relativo es un poco menos de 1/2⁴, por lo que la estimación es buena a 4+ bits.

Estimación ${displaystyle a}$ bueno a 8 bits se puede obtener por la búsqueda de mesa en los 8 bits altos de ${displaystyle a}$ , recordando que la parte alta es implícita en la mayoría de las representaciones de puntos flotantes, y la parte inferior de los 8 debe ser redondeado. La tabla es de 256 bytes de valores de raíz cuadrados precomputados de 8 bits. Por ejemplo, para el índice 11101101₂ representación 1.8515625₁₀, la entrada es 10101110₂ 1.359375₁₀, la raíz cuadrada de 1.8515625₁₀ a 8 bits de precisión (2+ dígitos decimales).

Método de Herón

El primer algoritmo explícito para aproximarse ${displaystyle {sqrt {S}}}$ es conocido como Heron método, después del primer siglo Héroe matemático griego de Alejandría que describió el método en su trabajo AD 60 Metrica. Este método también se llama Método babilónico (para no confundirse con el método babilónico para las hipotenuas aproximadas), aunque no hay evidencia de que el método era conocido por los babilonios.

Dado un número real positivo ${displaystyle S}$ , vamos $x 0 ■ 0$ ser cualquier estimación inicial positiva. El método de Heron consiste en calcular iterativamente

{displaystyle x_{n+1}={frac {1}{2}}left(x_{n}+{frac {S}{x_{n}}}right),}

{displaystyle (x_{n})}

{displaystyle lim _{nto infty }x_{n}={sqrt {S}}}

Esto equivale a usar el método de Newton para resolver ${displaystyle x^{2}-S=0}$ . Este algoritmo es cuantificadamente convergente: el número de dígitos correctos de ${displaystyle x_{n}}$ aproximadamente se dobla con cada iteración.

Derivación

La idea básica es que si $x$ es una sobreestimación de la raíz cuadrada de un número real no negativo $S$ luego $S / x$ será una subestimación, y viceversa, por lo que se puede esperar razonablemente que el promedio de estos dos números proporcione una mejor aproximación (aunque la prueba formal de esa afirmación depende de la desigualdad de medias aritméticas y geométricas que muestra que este promedio es siempre una sobreestimación de la raíz cuadrada, como se señala en el artículo sobre raíces cuadradas, asegurando así la convergencia).

Más precisamente, si $x$ es nuestra primera suposición de ${displaystyle {sqrt {S}}}$ y $ε$ es el error en nuestra estimación tal que $S = x + ε) 2$ , entonces podemos expandir el binomio

{displaystyle (x+varepsilon)^{2}=x^{2}+2xvarepsilon +varepsilon ^{2}}

{displaystyle varepsilon ={frac {S-x^{2}}{2x+varepsilon }}approx {frac {S-x^{2}}{2x}},}

desde entonces

{displaystyle varepsilon ll x}

Por lo tanto, podemos compensar el error y actualizar nuestra estimación anterior según corresponda.

{displaystyle x+varepsilon approx x+{frac {S-x^{2}}{2x}}={frac {S+x^{2}}{2x}}={frac {{frac {S}{x}}+x}{2}}equiv x_{text{revised}}}

Este algoritmo funciona igualmente bien en los números p-ádicos, pero no se puede utilizar para identificar raíces cuadradas reales con $p$ - raíces cuadradas ádicas; uno puede, por ejemplo, construir una secuencia de números racionales mediante este método que converja a +3 en los reales, pero a −3 en los 2-ádicos.

Ejemplo

Para calcular $\sqrt S$ , donde $S$ = 125348, con seis cifras significativas, utilice la estimación aproximada método anterior para obtener

{displaystyle {begin{aligned}{begin{array}{rlll}x_{0}&=6cdot 10^{2}&&=600.000\[0.3em]x_{1}&={frac {1}{2}}left(x_{0}+{frac {S}{x_{0}}}right)&={frac {1}{2}}left(600.000+{frac {125348}{600.000}}right)&=404.457\[0.3em]x_{2}&={frac {1}{2}}left(x_{1}+{frac {S}{x_{1}}}right)&={frac {1}{2}}left(404.457+{frac {125348}{404.457}}right)&=357.187\[0.3em]x_{3}&={frac {1}{2}}left(x_{2}+{frac {S}{x_{2}}}right)&={frac {1}{2}}left(357.187+{frac {125348}{357.187}}right)&=354.059\[0.3em]x_{4}&={frac {1}{2}}left(x_{3}+{frac {S}{x_{3}}}right)&={frac {1}{2}}left(354.059+{frac {125348}{354.059}}right)&=354.045\[0.3em]x_{5}&={frac {1}{2}}left(x_{4}+{frac {S}{x_{4}}}right)&={frac {1}{2}}left(354.045+{frac {125348}{354.045}}right)&=354.045end{array}}end{aligned}}}

Por lo tanto, $\sqrt 125348 \approx 354.045$ .

Convergencia

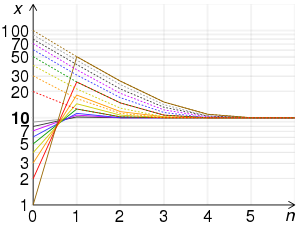
Supongamos que x₀ " 0 " S ■ 0. Entonces para cualquier número natural n, x_n ■ 0. Dejar el error relativo en x_n se define por

-1}" display="block" xmlns="http://www.w3.org/1998/Math/MathML">ε ε n=xnS− − 1■− − 1{displaystyle varepsilon ¿Qué? {x_{n}{sqrt {S}}-1}-1}" aria-hidden="true" class="mwe-math-fallback-image-display mw-invert" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1619871bd58a6d221947da5c43ce558c97576e58" style="vertical-align: -2.838ex; width:19.744ex; height:5.676ex;"/>

{displaystyle x_{n}={sqrt {S}}cdot (1+varepsilon _{n}).}

Entonces se puede demostrar que

{displaystyle varepsilon _{n+1}={frac {varepsilon _{n}^{2}}{2(1+varepsilon _{n})}}geq 0.}

Y así eso

{displaystyle varepsilon _{n+2}leq min left{{frac {varepsilon _{n+1}^{2}}{2}},{frac {varepsilon _{n+1}}{2}}right}}

El peor caso para la convergencia

Si se utiliza la estimación aproximada anterior con el método babilónico, los casos menos precisos en orden ascendente son los siguientes:

<math alttext="{displaystyle {begin{aligned}S&=1;&x_{0}&=2;&x_{1}&=1.250;&varepsilon _{1}&=0.250.\S&=10;&x_{0}&=2;&x_{1}&=3.500;&varepsilon _{1}&<0.107.\S&=10;&x_{0}&=6;&x_{1}&=3.833;&varepsilon _{1}&<0.213.\S&=100;&x_{0}&=6;&x_{1}&=11.333;&varepsilon _{1}&S=1;x0=2;x1=1.250;ε ε 1=0.250.S=10;x0=2;x1=3.500;ε ε 1c)0.107.S=10;x0=6;x1=3.833;ε ε 1c)0.213.S=100;x0=6;x1=11.333;ε ε 1c)0.134.{displaystyle {begin{aligned}S sensible=1; recíprocax_{0} reducida=2; recíprocax_{1} limit=1.250; ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################ ################################################################################################################################################################################################################################################################ - ¿Qué?<img alt="{displaystyle {begin{aligned}S&=1;&x_{0}&=2;&x_{1}&=1.250;&varepsilon _{1}&=0.250.\S&=10;&x_{0}&=2;&x_{1}&=3.500;&varepsilon _{1}&<0.107.\S&=10;&x_{0}&=6;&x_{1}&=3.833;&varepsilon _{1}&<0.213.\S&=100;&x_{0}&=6;&x_{1}&=11.333;&varepsilon _{1}&

Por lo tanto, en cualquier caso,

<math alttext="{displaystyle {begin{aligned}varepsilon _{1}&leq 2^{-2}.\varepsilon _{2}&<2^{-5}<10^{-1}.\varepsilon _{3}&<2^{-11}<10^{-3}.\varepsilon _{4}&<2^{-23}<10^{-6}.\varepsilon _{5}&<2^{-47}<10^{-14}.\varepsilon _{6}&<2^{-95}<10^{-28}.\varepsilon _{7}&<2^{-191}<10^{-57}.\varepsilon _{8}&<2^{-383}ε ε 1≤ ≤ 2− − 2.ε ε 2c)2− − 5c)10− − 1.ε ε 3c)2− − 11c)10− − 3.ε ε 4c)2− − 23c)10− − 6.ε ε 5c)2− − 47c)10− − 14.ε ε 6c)2− − 95c)10− − 28.ε ε 7c)2− − 191c)10− − 57.ε ε 8c)2− − 383c)10− − 115.{displaystyle {begin{aligned}varepsilon - ¿Qué? - ¿Qué? - ¿Qué? - ¿Qué? - ¿Qué? - ¿Qué? - ¿Qué? - ¿Qué?<img alt="{displaystyle {begin{aligned}varepsilon _{1}&leq 2^{-2}.\varepsilon _{2}&<2^{-5}<10^{-1}.\varepsilon _{3}&<2^{-11}<10^{-3}.\varepsilon _{4}&<2^{-23}<10^{-6}.\varepsilon _{5}&<2^{-47}<10^{-14}.\varepsilon _{6}&<2^{-95}<10^{-28}.\varepsilon _{7}&<2^{-191}<10^{-57}.\varepsilon _{8}&<2^{-383}

Los errores de redondeo ralentizarán la convergencia. Se recomienda mantener al menos un dígito adicional más allá de la precisión deseada del $x n$ que se está calculando. para minimizar el error de redondeo.

Método Bakhshali

Este método para encontrar una aproximación a una raíz cuadrada fue descrito en un antiguo manuscrito indio, llamado el manuscrito Bakhshali. Es equivalente a dos iteraciones del método babilónico comenzando con x₀. Por lo tanto, el algoritmo es quartically convergent, lo que significa que el número de dígitos correctos de la aproximación cuadruple aproximadamente con cada iteración. La presentación original, utilizando la notación moderna, es la siguiente: Para calcular ${displaystyle {sqrt {S}}}$ , vamos ${displaystyle x_{0}^{2}}$ ser la aproximación inicial a ${displaystyle S}$ . Entonces, sucesivamente iterate como:

{displaystyle {begin{aligned}a_{n}&={frac {S-x_{n}^{2}}{2x_{n}}},\b_{n}&=x_{n}+a_{n},\x_{n+1}&=b_{n}-{frac {a_{n}^{2}}{2b_{n}}}=(x_{n}+a_{n})-{frac {a_{n}^{2}}{2(x_{n}+a_{n})}}.end{aligned}}}

Esto se puede utilizar para construir una aproximación racional a la raíz cuadrada al principio con un entero. Si ${displaystyle x_{0}=N}$ es un entero elegido así ${displaystyle N^{2}}$ está cerca ${displaystyle S}$ , y ${displaystyle d=S-N^{2}}$ es la diferencia cuyo valor absoluto se minimiza, entonces la primera iteración se puede escribir como:

{displaystyle {sqrt {S}}approx N+{frac {d}{2N}}-{frac {d^{2}}{8N^{3}+4Nd}}={frac {8N^{4}+8N^{2}d+d^{2}}{8N^{3}+4Nd}}={frac {N^{4}+6N^{2}S+S^{2}}{4N^{3}+4NS}}={frac {N^{2}(N^{2}+6S)+S^{2}}{4N(N^{2}+S)}}.}

El método Bakhshali se puede generalizar al cálculo de una raíz arbitraria, incluidas raíces fraccionarias.

Ejemplo

Usando el mismo ejemplo que se da con el método babilónico, ${displaystyle S=125348.}$ Entonces, la primera iteración da

{displaystyle {begin{aligned}x_{0}&=600\[1ex]a_{1}&={frac {125348-600^{2}}{2times 600}}&&=&-195.543\[1ex]b_{1}&=600+(-195.543)&&=&404.456\[1ex]x_{1}&=404.456-{frac {(-195.543)^{2}}{2times 404.456}}&&=&357.186end{aligned}}}

Del mismo modo, la segunda iteración da

{displaystyle {begin{aligned}a_{2}&={frac {125348-357.186^{2}}{2times 357.186}}&&=&-3.126\[1ex]b_{2}&=357.186+(-3.126)&&=&354.060\[1ex]x_{2}&=354.06-{frac {(-3.1269)^{2}}{2times 354.06}}&&=&354.046end{aligned}}}

Cálculo de dígitos por dígitos

Este es un método para encontrar cada dígito de la raíz cuadrada en una secuencia. Este método se basa en el teorema binomio y básicamente en una solución de algoritmo inverso ${displaystyle (x+y)^{2}=x^{2}+2xy+y^{2}}$ . Es más lento que el método babilónico, pero tiene varias ventajas:

Puede ser más fácil para los cálculos manuales.
Cada dígito de la raíz encontrada se sabe que es correcto, es decir, no tiene que ser cambiado más adelante.
Si la raíz cuadrada tiene una expansión que termina, el algoritmo termina después de encontrar el último dígito. Por lo tanto, se puede utilizar para comprobar si un entero dado es un número cuadrado.
El algoritmo funciona para cualquier base, y naturalmente, la forma en que procede depende de la base elegida.

Las desventajas son:

Se vuelve inmanejable para las raíces superiores.
No tolera adivinaciones o subcalculaciones inexactas; tales errores conducen a cada dígito siguiente del resultado siendo incorrecto, a diferencia del método de Newton, que autocorrige cualquier error de aproximación.
Aunque el cálculo de dígitos por dígitos es suficientemente eficiente en papel, es demasiado caro para las implementaciones de software. Cada iteración implica números mayores, que requieren más memoria, pero sólo avanza la respuesta por un dígito correcto. Así, el algoritmo toma más tiempo para cada dígito adicional.

Los huesos de Napier incluyen una ayuda para la ejecución de este algoritmo. El algoritmo de raíz n-ésima cambiante es una generalización de este método.

Principio básico

Primero, considere el caso de encontrar la raíz cuadrada de un número $Z$ , es decir, el cuadrado de un número de dos dígitos $XY$ , donde $X$ es el dígito de las decenas y $Y$ es el dígito de las unidades. Específicamente:

{displaystyle Z=left(10X+Yright)^{2}=100X^{2}+20XY+Y^{2}}

Ahora, usando el algoritmo dígito por dígito, primero determinamos el valor de $X$ . $X$ es el dígito más grande tal que $X 2$ es menor o igual a $Z$ del cual eliminamos los dos dígitos más a la derecha.

En la siguiente iteración, emparejamos los dígitos, multiplicamos $X$ por 2 y lo colocamos en el lugar de las décimas mientras intente averiguar cuál es el valor de $Y$ .

Dado que este es un caso simple donde la respuesta es una raíz cuadrada perfecta $XY$ , el algoritmo se detiene aquí.

La misma idea se puede extender a cualquier cálculo arbitrario de raíz cuadrada a continuación. Supongamos que podemos encontrar la raíz cuadrada de $N$ expresándola como una suma de n números positivos tales que

{displaystyle N=left(a_{1}+a_{2}+a_{3}+dots +a_{n}right)^{2}.}

Aplicando repetidamente la identidad básica

{displaystyle (x+y)^{2}=x^{2}+2xy+y^{2},}

{displaystyle {begin{aligned}&(a_{1}+a_{2}+a_{3}+dotsb +a_{n})^{2}\=&,a_{1}^{2}+2a_{1}a_{2}+a_{2}^{2}+2(a_{1}+a_{2})a_{3}+a_{3}^{2}+dots +a_{n-1}^{2}+2left(sum _{i=1}^{n-1}a_{i}right)a_{n}+a_{n}^{2}\=&,a_{1}^{2}+[2a_{1}+a_{2}]a_{2}+[2(a_{1}+a_{2})+a_{3}]a_{3}+dots +left[2left(sum _{i=1}^{n-1}a_{i}right)+a_{n}right]a_{n}.end{aligned}}}

Esta expresión nos permite encontrar la raíz cuadrada adivinando secuencialmente los valores de ${displaystyle a_{i}}$ s. Supongamos que los números ${displaystyle a_{1},ldotsa_{m-1}}$ ya se han adivinado, entonces el m-el término del lado derecho de la suma anterior es dado por ${displaystyle Y_{m}=left[2P_{m-1}+a_{m}right]a_{m},}$ Donde ${textstyle P_{m-1}=sum _{i=1}^{m-1}a_{i}}$ es la raíz cuadrada aproximada encontrada hasta ahora. Ahora cada nueva suposición ${displaystyle a_{m}}$ debe satisfacer la recursión

{displaystyle X_{m}=X_{m-1}-Y_{m},}

{displaystyle X_{m}geq 0}

{displaystyle 1leq mleq n,}

{displaystyle X_{0}=N.}

{displaystyle X_{n}=0,}

{displaystyle a_{i}}

{displaystyle X_{n}}

Por ejemplo, en el sistema numérico decimal tenemos

{displaystyle N=left(a_{1}cdot 10^{n-1}+a_{2}cdot 10^{n-2}+cdots +a_{n-1}cdot 10+a_{n}right)^{2},}

{displaystyle 10^{n-i}}

{displaystyle a_{i}in {0,1,2,ldots9}}

{displaystyle P_{m-1}}

{displaystyle Y_{m}}

{displaystyle P_{m-1}=sum _{i=1}^{m-1}a_{i}cdot 10^{n-i}=10^{n-m+1}sum _{i=1}^{m-1}a_{i}cdot 10^{m-i-1},}

{displaystyle Y_{m}=left[2P_{m-1}+a_{m}cdot 10^{n-m}right]a_{m}cdot 10^{n-m}=left[20sum _{i=1}^{m-1}a_{i}cdot 10^{m-i-1}+a_{m}right]a_{m}cdot 10^{2(n-m)}.}

Aquí desde el valor del lugar ${displaystyle Y_{m}}$ es un poder uniforme de 10, sólo necesitamos trabajar con el par de dígitos más significativos del término restante ${displaystyle X_{m-1}}$ en cualquier etapa m. La sección que figura a continuación codifica este procedimiento.

Es obvio que un método similar se puede utilizar para calcular la raíz cuadrada en sistemas de números distintos del sistema de número decimal. Por ejemplo, encontrar la raíz cuadrada dígitos por dígitos en el sistema de números binarios es bastante eficiente ya que el valor de ${displaystyle a_{i}}$ es buscado desde un pequeño conjunto de dígitos binarios {0,1}. Esto hace que el cálculo sea más rápido ya que en cada etapa el valor de ${displaystyle Y_{m}}$ o ${displaystyle Y_{m}=0}$ para ${displaystyle a_{m}=0}$ o ${displaystyle Y_{m}=2P_{m-1}+1}$ para ${displaystyle a_{m}=1}$ . El hecho de que tengamos sólo dos opciones posibles ${displaystyle a_{m}}$ hace también el proceso de decidir el valor de ${displaystyle a_{m}}$ a m- la etapa de cálculo más fácil. Esto es porque sólo necesitamos comprobar si ${displaystyle Y_{m}leq X_{m-1}}$ para ${displaystyle a_{m}=1.}$ Si esta condición está satisfecha, entonces tomamos ${displaystyle a_{m}=1}$ ; si no ${displaystyle a_{m}=0.}$ Además, el hecho de que la multiplicación por 2 se realiza mediante cambios de bits izquierdos ayuda en el cálculo.

Decimal (base 10)

Escribe el número original en forma decimal. Los números se escriben de manera similar al algoritmo de división larga y, como en la división larga, la raíz se escribirá en la línea de arriba. Ahora separe los dígitos en pares, comenzando desde el punto decimal y yendo hacia la izquierda y hacia la derecha. El punto decimal de la raíz estará encima del punto decimal del cuadrado. Un dígito de la raíz aparecerá encima de cada par de dígitos del cuadrado.

Comenzando con el par de dígitos más a la izquierda, realice el siguiente procedimiento para cada par:

A partir de la izquierda, derriba el par de dígitos más significativo (izquierda) aún no usado (si todos los dígitos se han utilizado, escriba "00") y escríbalos a la derecha del resto del paso anterior (en el primer paso, no habrá ningún resto). En otras palabras, multiplicar el resto por 100 y añadir los dos dígitos. Este será el valor actual c.
Encontrar p, Sí. y x, como sigue:
- Vamos. p ser el parte de la raíz encontrada hasta ahora, ignorando cualquier punto decimal. (Para el primer paso, p = 0.)
- Determinar el mayor dígito x tales que x()20p+x)≤ ≤ c{displaystyle x(20p+x)leq c} ${displaystyle x(20p+x)leq c}$ . Usaremos una nueva variable Sí. = x(20)p + x).
  - Nota: 20p + x es simplemente dos veces p, con el dígito x a la derecha.
  - Nota: x se puede encontrar adivinando lo que c/(20·p) es y hacer un cálculo de prueba de Sí., luego ajuste x hacia arriba o hacia abajo, según sea necesario.
- Coloque el dígito ${displaystyle x}$ como el siguiente dígito de la raíz, es decir, sobre los dos dígitos de la plaza que acaba de bajar. Así, el siguiente p será el viejo p veces 10 más x.
Subtract Sí. desde c para formar un nuevo resto.
Si el resto es cero y no hay más dígitos para bajar, entonces el algoritmo ha terminado. De lo contrario, vuelve al paso 1 para otra iteración.

Ejemplos

Encuentra la raíz cuadrada de 152,2756.

  1 2. 3 4 /
/ 01 52.27 56

01 1*1 0 0 0 0 0 0 2*2 x=1
  01  y = x*x = 1*1 = 1
52 22*2
  00 44  y = (20+x)*x = 22*2 = 44
08 27 243*3
  07 29  y = (240+x)*x = 243*3 = 729
98 56 2464*4
  98 56  y = (2460+x)*x = 2464*4 = 9856
00 El algoritmo termina: Answer=12.34

Sistema de numeración binario (base 2)

Esta sección utiliza el formalismo de la sección de cálculo dígitos por dígitos arriba, con la leve variación que dejamos ${displaystyle N^{2}=(a_{n}+dotsb +a_{0})^{2}}$ , con cada ${displaystyle a_{m}=2^{m}}$ o ${displaystyle a_{m}=0}$ .
Nosotros lo hacemos todo ${displaystyle 2^{m}}$ , de ${displaystyle 2^{n}}$ abajo ${displaystyle 2^{0}}$ , y construir una solución aproximada ${displaystyle P_{m}=a_{n}+a_{n-1}+ldots +a_{m}}$ , la suma de todo ${displaystyle a_{i}}$ por lo que hemos determinado el valor.
Para determinar si ${displaystyle a_{m}}$ iguales ${displaystyle 2^{m}}$ o ${displaystyle 0}$ , lo dejamos ${displaystyle P_{m}=P_{m+1}+2^{m}}$ . Si ${displaystyle P_{m}^{2}leq N^{2}}$ (es decir, el cuadrado de nuestra solución aproximada incluyendo ${displaystyle 2^{m}}$ no excede el cuadrado de destino) entonces ${displaystyle a_{m}=2^{m}}$ , de lo contrario ${displaystyle a_{m}=0}$ y ${displaystyle P_{m}=P_{m+1}}$ .
Para evitar el escuadrón ${displaystyle P_{m}}$ en cada paso, almacenamos la diferencia ${displaystyle X_{m}=N^{2}-P_{m}^{2}}$ y la actualización incremental por el ajuste ${displaystyle X_{m}=X_{m+1}-Y_{m}}$ con ${displaystyle Y_{m}=P_{m}^{2}-P_{m+1}^{2}=2P_{m+1}a_{m}+a_{m}^{2}}$ .
Inicialmente, nos fijamos ${displaystyle a_{n}=P_{n}=2^{n}}$ para el más grande ${displaystyle n}$ con ${displaystyle (2^{n})^{2}=4^{n}leq N^{2}}$ .

Como una optimización extra, almacenamos ${displaystyle P_{m+1}2^{m+1}}$ y ${displaystyle (2^{m})^{2}}$ , los dos términos ${displaystyle Y_{m}}$ en caso de que ${displaystyle a_{m}}$ no es cero, en variables separadas ${displaystyle c_{m}}$ , ${displaystyle d_{m}}$ :

{displaystyle c_{m}=P_{m+1}2^{m+1}}

{displaystyle d_{m}=(2^{m})^{2}}

{displaystyle Y_{m}={begin{cases}c_{m}+d_{m}&{text{if }}a_{m}=2^{m}\0&{text{if }}a_{m}=0end{cases}}}

${displaystyle c_{m}}$ y ${displaystyle d_{m}}$ se puede actualizar eficientemente en cada paso:

{displaystyle c_{m-1}=P_{m}2^{m}=(P_{m+1}+a_{m})2^{m}=P_{m+1}2^{m}+a_{m}2^{m}={begin{cases}c_{m}/2+d_{m}&{text{if }}a_{m}=2^{m}\c_{m}/2&{text{if }}a_{m}=0end{cases}}}

{displaystyle d_{m-1}={frac {d_{m}}{4}}}

Tenga en cuenta que:

{displaystyle c_{-1}=P_{0}2^{0}=P_{0}=N,}

Una implementación de este algoritmo en C:

int32_t isqrt()int32_t n) {} afirmación(()"La entrada sqrt debe ser no negativo", n ■ 0)); // X_(n+1) int32_t x = n; // c_n int32_t c = 0; // d_n que comienza a la potencia más alta de cuatro int32_t d = 1 c) c) 30; // La segunda parte está lista. // Lo mismo que (sin firmar) INT32_MAX + 1) / 2. mientras ()d ■ n) {} d > 2; } // para dn ... d0 mientras ()d ! 0) {} si ()x >= c + d) {} // si X_(m+1) ≥ Y_m entonces a_m = 2^m x -= c + d; // X_m = X_(m+1) - Y_m c = ()c " 1) + d; // c_(m-1) = c_m/2 + d_m (a_m es 2^m) } más {} c > 1; // c_(m-1) = c_m/2 (am es 0) } d > 2; // d_(m-1) = d_m/4 } Regreso c; // c_(-1)}

Se pueden lograr algoritmos más rápidos, en binario y decimal o cualquier otra base, utilizando tablas de búsqueda, lo que de hecho intercambia más espacio de almacenamiento por un tiempo de ejecución reducido.

Identidad exponencial

Las calculadoras de bolsillo normalmente implementan buenas rutinas para calcular la función exponencial y el logaritmo natural, y luego computar la raíz cuadrada S usando la identidad encontrada usando las propiedades de los logaritmos ( ${displaystyle ln x^{n}=nln x}$ ) y exponenciales ( ${displaystyle e^{ln x}=x}$ ):

{displaystyle {sqrt {S}}=e^{{frac {1}{2}}ln S}.}

Un método iterativo de dos variables

Este método es aplicable para encontrar la raíz cuadrada $<math alttext="{displaystyle 0<S0c)Sc)3{displaystyle 0 realizadasS won3,!} <img alt="{displaystyle 0<S$ y converge mejor para ${displaystyle Sapprox 1}$ . Esto, sin embargo, no es una limitación real para un cálculo basado en la computadora, como en las representaciones de punto flotante y punto fijo base 2, es trivial multiplicarse ${displaystyle S,!}$ por un poder entero de 4, y por tanto ${displaystyle {sqrt {S}}}$ por el poder correspondiente de 2, cambiando el exponente o cambiando, respectivamente. Por lo tanto, ${displaystyle S,!}$ se puede mover a la gama $<math alttext="{textstyle {tfrac {1}{2}}leq S12≤ ≤ Sc)2{fnMicrosoft}}leq S.<img alt="{textstyle {tfrac {1}{2}}leq S$ . Además, el siguiente método no emplea divisiones generales, sino solamente adiciones, restas, multiplicaciones y divisiones por poderes de dos, que son otra vez triviales para implementar. Una desventaja del método es que los errores numéricos se acumulan, en contraste con métodos iterativos variables individuales como el babilónico.

El paso inicial de este método es

{displaystyle {begin{aligned}a_{0}&=S\c_{0}&=S-1end{aligned}}}

{displaystyle {begin{aligned}a_{n+1}&=a_{n}-a_{n}c_{n}/2\c_{n+1}&=c_{n}^{2}(c_{n}-3)/4end{aligned}}}

{displaystyle a_{n}to {sqrt {S}}}

{displaystyle c_{n}to 0}

La convergencia de ${displaystyle c_{n},!}$ , y por lo tanto también de ${displaystyle a_{n},!}$ , es cuadrático.

La prueba del método es bastante fácil. Primero, reescribir la definición iterativa de ${displaystyle c_{n}}$ como

{displaystyle 1+c_{n+1}=(1+c_{n})(1-{tfrac {1}{2}}c_{n})^{2}.}

{displaystyle S(1+c_{n})=a_{n}^{2}}

{displaystyle a_{n},!}

{displaystyle {sqrt {S}}}

{displaystyle c_{n},!}

<math alttext="{displaystyle -1<c_{0}− − 1c)c0c)2{displaystyle -1 sec_{0} se hizo 2,!<img alt="{displaystyle -1<c_{0}

Este método fue desarrollado alrededor de 1950 por M. V. Wilkes, D. J. Wheeler y S. Gill para su uso en EDSAC, una de las primeras computadoras electrónicas. Posteriormente, el método se generalizó, permitiendo el cálculo de raíces no cuadradas.

Métodos iterativos para raíces cuadradas recíprocas

Los siguientes son métodos iterativos para encontrar la raíz cuadrada recíproca S que es ${displaystyle 1/{sqrt {S}}}$ . Una vez que se ha encontrado, encontrar ${displaystyle {sqrt {S}}}$ por simple multiplicación: ${displaystyle {sqrt {S}}=Scdot (1/{sqrt {S}})}$ . Estas iteraciones implican solamente multiplicación, y no división. Por lo tanto, son más rápidos que el método babilónico. Sin embargo, no son estables. Si el valor inicial no está cerca de la raíz cuadrada recíproca, las iteraciones se apartarán de ella en lugar de converger con ella. Por lo tanto, puede ser ventajoso realizar una iteración del método babilónico en una estimación aproximada antes de comenzar a aplicar estos métodos.

Aplicar el método de Newton a la ecuación ${displaystyle (1/x^{2})-S=0}$ produce un método que converge cuadráticamente utilizando tres multiplicaciones por paso: ${displaystyle x_{n+1}={frac {x_{n}}{2}}cdot (3-Scdot x_{n}^{2})=x_{n}cdot left({frac {3}{2}}-{frac {S}{2}}cdot x_{n}^{2}right).}$
Otra iteración es obtenida por el método de Halley, que es el método del orden dos del titular. Esto converge cúbicamente, pero implica cinco multiplicaciones por iteración: ${displaystyle y_{n}=Scdot x_{n}^{2},}$ y ${displaystyle x_{n+1}={frac {x_{n}}{8}}cdot (15-y_{n}cdot (10-3cdot y_{n}))=x_{n}cdot left({frac {15}{8}}-y_{n}cdot left({frac {10}{8}}-{frac {3}{8}}cdot y_{n}right)right).}$
Si hace aritmética de punto fijo, la multiplicación por 3 y división por 8 puede implementarse usando cambios y adiciones. Si utiliza el punto flotante, el método de Halley puede reducirse a cuatro multiplicaciones por iteración por precomputación ${textstyle {sqrt {3/8}}S}$ y ajustando todas las otras constantes para compensar: ${displaystyle y_{n}={sqrt {frac {3}{8}}}Scdot x_{n}^{2},}$ y ${displaystyle x_{n+1}=x_{n}cdot left({frac {15}{8}}-y_{n}cdot left({sqrt {frac {25}{6}}}-y_{n}right)right).}$

Algoritmo de Goldschmidt

Algunos ordenadores utilizan el algoritmo de Goldschmidt para calcular simultáneamente ${displaystyle {sqrt {S}}}$ y ${displaystyle 1/{sqrt {S}}}$ . El algoritmo de Goldschmidt encuentra ${displaystyle {sqrt {S}}}$ más rápido que la iteración Newton-Raphson en un ordenador con una instrucción multiplicada fusionada y una unidad de punto flotante o dos unidades independientes de punto flotante.

Comienza la primera forma de escribir el algoritmo de Goldschmidt

{displaystyle b_{0}=S}

{displaystyle Y_{0}approx 1/{sqrt {S}}}

(típicamente usando una búsqueda de tabla)

{displaystyle y_{0}=Y_{0}}

{displaystyle x_{0}=Sy_{0}}

e itera

{displaystyle {begin{aligned}b_{n+1}&=b_{n}Y_{n}^{2}\Y_{n+1}&={tfrac {1}{2}}(3-b_{n+1})\x_{n+1}&=x_{n}Y_{n+1}\y_{n+1}&=y_{n}Y_{n+1}end{aligned}}}

{displaystyle b_{i}}

{displaystyle lim _{nto infty }x_{n}={sqrt {S}},}

{displaystyle lim _{nto infty }y_{n}=1/{sqrt {S}}.}

{displaystyle x_{n}}

{displaystyle y_{n}}

{displaystyle x_{n}=Sy_{n}}

Comienza una segunda forma, que utiliza operaciones fusionadas de suma múltiple

{displaystyle y_{0}approx 1/{sqrt {S}}}

(típicamente usando una búsqueda de tabla)

{displaystyle x_{0}=Sy_{0}}

{displaystyle h_{0}={tfrac {1}{2}}y_{0}}

e itera

{displaystyle {begin{aligned}r_{n}&=0.5-x_{n}h_{n}\x_{n+1}&=x_{n}+x_{n}r_{n}\h_{n+1}&=h_{n}+h_{n}r_{n}end{aligned}}}

{displaystyle r_{i}}

{displaystyle lim _{nto infty }x_{n}={sqrt {S}},}

{displaystyle lim _{nto infty }2h_{n}=1/{sqrt {S}}.}

Serie Taylor

Si N es una aproximación a ${displaystyle {sqrt {S}}}$ , una mejor aproximación se puede encontrar utilizando la serie Taylor de la función raíz cuadrada:

{displaystyle {sqrt {N^{2}+d}}=Nsum _{n=0}^{infty }{frac {(-1)^{n}(2n)!}{(1-2n)n!^{2}4^{n}}}{frac {d^{n}}{N^{2n}}}=Nleft(1+{frac {d}{2N^{2}}}-{frac {d^{2}}{8N^{4}}}+{frac {d^{3}}{16N^{6}}}-{frac {5d^{4}}{128N^{8}}}+cdots right)}

Como método iterativo, el orden de convergencia es igual al número de términos utilizados. Con dos términos, es idéntico al método babilónico. Con tres términos, cada iteración toma casi tantas operaciones como la aproximación Bakhshali, pero converge más lentamente. Por lo tanto, esta no es una forma de cálculo particularmente eficiente. Para maximizar la tasa de convergencia, elija $N$ así ${displaystyle {frac {|d|}{N^{2}}},}$ es lo más pequeño posible.

Expansión de fracción continua

La representación de fracción continua de un número real se puede utilizar en lugar de su expansión decimal o binaria y esta representación tiene la propiedad de que la raíz cuadrada de cualquier número racional (que aún no sea un cuadrado perfecto) tiene una expansión periódica y repetida. , similar a cómo los números racionales tienen expansiones repetidas en el sistema de notación decimal.

irracionales cuadráticos (números de la forma ${displaystyle {frac {a+{sqrt {b}}}{c}}}$ , donde a, b y c son enteros), y en particular, raíces cuadradas de enteros, tienen fracciones continuas periódicas. A veces lo que se desea no es encontrar el valor numérico de una raíz cuadrada, sino más bien su continua expansión de la fracción, y por lo tanto su aproximación racional. Vamos. S ser el número positivo para el cual estamos obligados a encontrar la raíz cuadrada. Entonces suponiendo a ser un número que sirve como una conjetura inicial y r para ser el término restante, podemos escribir ${displaystyle S=a^{2}+r.}$ Desde que tenemos ${displaystyle S-a^{2}=({sqrt {S}}+a)({sqrt {S}}-a)=r}$ , podemos expresar la raíz cuadrada S como

{displaystyle {sqrt {S}}=a+{frac {r}{a+{sqrt {S}}}}.}

Al aplicar esta expresión para ${displaystyle {sqrt {S}}}$ al término denominador de la fracción, tenemos

{displaystyle {sqrt {S}}=a+{frac {r}{a+(a+{frac {r}{a+{sqrt {S}}}})}}=a+{frac {r}{2a+{frac {r}{a+{sqrt {S}}}}}}.}

Notación compacta

La expansión del numerador/denominador para fracciones continuas (véase la izquierda) es engorrosa para escribir, así como para incrustar en sistemas de formato de texto. Así que los matemáticos han ideado varias notaciones alternativas, como

{displaystyle {sqrt {S}}=a+{frac {r}{2a+}},{frac {r}{2a+}},{frac {r}{2a+}}cdots }

Cuando ${displaystyle r=1}$ una notación aún más compacta es:

{displaystyle [a;2a,2a,2a,cdots ]}

Para repetir fracciones continuas (que todas las raíces cuadradas de cuadrados no perfectos hacen), la repetición está representada sólo una vez, con un overline para significar una repetición no-terminante de la parte sobrelineada:

{displaystyle [a;{overline {2a}}]}

Para √2, el valor de ${displaystyle a}$ es 1, por lo que su representación es:

{displaystyle [1;{overline {2}}]}

Procediendo de esta manera, obtenemos una fracción continua generalizada para la raíz cuadrada como

{displaystyle {sqrt {S}}=a+{cfrac {r}{2a+{cfrac {r}{2a+{cfrac {r}{2a+ddots }}}}}}}

El primer paso para evaluar tal fracción para obtener una raíz es hacer sustituciones numéricas para la raíz del número deseado, y el número de denominadores seleccionados. Por ejemplo, en forma canónica, ${displaystyle r}$ 1 y 1 √2, ${displaystyle a}$ es 1, por lo que la fracción continua numérica para 3 denominadores es:

{displaystyle {sqrt {2}}approx 1+{cfrac {1}{2+{cfrac {1}{2+{cfrac {1}{2}}}}}}}

El paso 2 es reducir la fracción continua de abajo hacia arriba, un denominador a la vez, para producir una fracción racional cuyo numerador y denominador son enteros. Así pues, la reducción procede (teniendo los tres primeros denominadores):

{displaystyle {begin{aligned}1+{cfrac {1}{2+{cfrac {1}{2+{cfrac {1}{2}}}}}}&=1+{cfrac {1}{2+{cfrac {1}{frac {5}{2}}}}}\&=1+{cfrac {1}{2+{cfrac {2}{5}}}}=1+{cfrac {1}{frac {12}{5}}}\&=1+{cfrac {5}{12}}={frac {17}{12}}end{aligned}}}

Finalmente (paso 3), divide el numerador por el denominador de la fracción racional para obtener el valor aproximado de la raíz:

{displaystyle 17div 12=1.42}

El valor real de √2 es 1.41 a tres dígitos significativos. El error relativo es 0.17%, por lo que la fracción racional es buena a casi tres dígitos de precisión. Tomar más denominadores da sucesivamente mejores aproximaciones: cuatro denominadores produce la fracción ${displaystyle {frac {41}{29}}=1.4137}$ , bueno a casi 4 dígitos de precisión, etc.

Los siguientes son ejemplos de raíces cuadradas, sus fracciones continuas simples y sus primeros términos, llamados convergentes, hasta el denominador 99 inclusive:

√S	~decimal	fracción continua	convergentes
√2	1.41421	${displaystyle [1;{overline {2}}]}$	${displaystyle {frac {3}{2}},{frac {7}{5}},{frac {17}{12}},{frac {41}{29}},{frac {99}{70}}}$
√3	1.73205	${displaystyle [1;{overline {1,2}}]}$	${displaystyle {frac {2}{1}},{frac {5}{3}},{frac {7}{4}},{frac {19}{11}},{frac {26}{15}},{frac {71}{41}},{frac {97}{56}}}$
√5	2.23607	${displaystyle [2;{overline {4}}]}$	${displaystyle {frac {9}{4}},{frac {38}{17}},{frac {161}{72}}}$
√6	2.44949	${displaystyle [2;{overline {2,4}}]}$	${displaystyle {frac {5}{2}},{frac {22}{9}},{frac {49}{20}},{frac {218}{89}}}$
√10	3.16228	${displaystyle [3;{overline {6}}]}$	${displaystyle {frac {19}{6}},{frac {117}{37}}}$
${displaystyle {sqrt {pi }}}$	1.77245	${displaystyle [1;1,3,2,1,1,6...]}$	${displaystyle {frac {2}{1}},{frac {7}{4}},{frac {16}{9}},{frac {23}{13}},{frac {39}{22}}}$
${displaystyle {sqrt {e}}}$	1.64872	${displaystyle [1;1,1,1,5,1,1...]}$	${displaystyle {frac {2}{1}},{frac {3}{2}},{frac {5}{3}},{frac {28}{17}},{frac {33}{20}},{frac {61}{37}}}$
${displaystyle {sqrt {phi }}}$	1.27202	${displaystyle [1;3,1,2,11,3,7...]}$	${displaystyle {frac {4}{3}},{frac {5}{4}},{frac {14}{11}}}$

En general, cuanto mayor sea el denominador de una fracción racional, mejor será la aproximación. También se puede demostrar que truncar una fracción continua produce una fracción racional que es la mejor aproximación a la raíz de cualquier fracción con denominador menor o igual al denominador de esa fracción; por ejemplo, ninguna fracción con un denominador menor o igual a 70 es una aproximación tan buena a √2 como 99/70.

Aproximaciones que dependen de la representación en coma flotante

Un número está representado en un formato de punto flotante como ${displaystyle mtimes b^{p}}$ que también se llama notación científica. Su raíz cuadrada ${displaystyle {sqrt {m}}times b^{p/2}}$ y fórmulas similares solicitarían raíces de cubo y logaritmos. En la cara de ella, esto no es mejora en la simplicidad, pero supone que sólo se requiere una aproximación: entonces sólo ${displaystyle b^{p/2}}$ es bueno para un orden de magnitud. Siguiente, reconocer que algunos poderes, $p$ , será extraño, por lo tanto para 3141.59 = 3.14159×10³ en lugar de tratar con poderes fraccionados de la base, multiplicar el mantissa por la base y restar uno del poder para hacerlo uniforme. La representación ajustada se convertirá en el equivalente a 31.4159×10² para que la raíz cuadrada sea √31.4159×10¹.

Si se toma la parte entera de la mantisa ajustada, solo pueden existir los valores del 1 al 99, y eso podría usarse como índice en una tabla de 99 raíces cuadradas precalculadas para completar la estimación. Una computadora que use base dieciséis requeriría una tabla más grande, pero una que use base dos requeriría sólo tres entradas: los posibles bits de la parte entera de la mantisa ajustada son 01 (siendo la potencia aún así no hubo desplazamiento, recordando que una computadora normalizada número de coma flotante siempre tiene un dígito de orden superior distinto de cero) o si la potencia era impar, 10 u 11, siendo estos los primeros dos bits de la mantisa original. Por lo tanto, 6,25 = 110,01 en binario, normalizado a 1,1001 × 2² una potencia par, por lo que los bits emparejados de la mantisa son 01, mientras que .625 = 0,101 en binario se normaliza a 1,01 × 2^{− 1} es una potencia impar, por lo que el ajuste es 10,1 × 2⁻² y los bits emparejados son 10. Observe que el bit de orden inferior de la potencia se repite en el bit de orden superior de la mantisa por pares. Una potencia par tiene su bit de orden inferior cero y la mantisa ajustada comenzará con 0, mientras que para una potencia impar ese bit es uno y la mantisa ajustada comenzará con 1. Así, cuando la potencia se reduce a la mitad, es como si El bit de orden inferior se desplaza para convertirse en el primer bit de la mantisa por pares.

Una tabla con sólo tres entradas podría ampliarse incorporando bits adicionales de la mantisa. Sin embargo, con las computadoras, en lugar de calcular una interpolación en una tabla, a menudo es mejor encontrar algún cálculo más simple que proporcione resultados equivalentes. Ahora todo depende de los detalles exactos del formato de la representación, además de qué operaciones están disponibles para acceder y manipular las partes del número. Por ejemplo, Fortran ofrece una función EXPONENT(x) para obtener el poder. El esfuerzo invertido en diseñar una buena aproximación inicial debe recuperarse evitando así las iteraciones adicionales del proceso de refinamiento que habrían sido necesarias para una mala aproximación. Dado que son pocos (una iteración requiere dividir, sumar y reducir a la mitad), la restricción es severa.

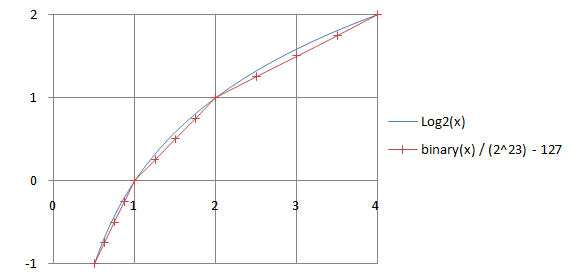
Muchos ordenadores siguen la representación de IEEE (o lo suficientemente similar), y una aproximación muy rápida a la raíz cuadrada se puede obtener para iniciar el método de Newton. La técnica que sigue se basa en el hecho de que el formato de punto flotante (en la base dos) aproxima el logaritmo base-2. Eso es ${displaystyle log _{2}(mtimes 2^{p})=p+log _{2}(m)}$

Así que para un número de punto flotante de precisión de 32 bits en formato IEEE (donde destaca, el poder tiene un sesgo de 127 añadido para la forma representada) se puede obtener el logaritmo aproximado interpretando su representación binaria como un entero de 32 bits, escalando por ${displaystyle 2^{-23}}$ , y quitar un sesgo de 127, es decir.

{displaystyle x_{text{int}}cdot 2^{-23}-127approx log _{2}(x).}

Por ejemplo, 1.0 está representado por un número hexadecimal 0x3F800000, que representaría ${displaystyle 1065353216=127cdot 2^{23}}$ si se toma como un entero. Usando la fórmula encima de usted consigue ${displaystyle 1065353216cdot 2^{-23}-127=0}$ , como se esperaba de ${displaystyle log _{2}(1.0)}$ . De forma similar obtienes 0,5 de 1,5 (0x3FC00000).

Para obtener la raíz cuadrada, dividir el logaritmo por 2 y convertir el valor de vuelta. El siguiente programa demuestra la idea. El bit más bajo del exponente se permite intencionadamente propagarse hacia el mantissa. Una manera de justificar los pasos de este programa es asumir ${displaystyle b}$ es el sesgo exponente y ${displaystyle n}$ es el número de bits explícitamente almacenados en el mantissa y luego mostrar que

{displaystyle left(left({tfrac {1}{2}}left(x_{text{int}}/2^{n}-bright)right)+bright)cdot 2^{n}={tfrac {1}{2}}left(x_{text{int}}-2^{n}right)+left({tfrac {1}{2}}left(b+1right)right)cdot 2^{n}.}

/* Supone que flotar está en el formato de punto flotante de precisión única IEEE 754 */#include Identificado.hflotador sqrt_approx()flotador z){}sindicato {} flotador f; uint32_t i; } val = {}z};/* Convertir tipo, preservando el patrón de bits *//** Para justificar el siguiente código, probar que** ((((val.i / 2^m) - b) / 2) + b) * 2^m = ((val.i - 2^m) / 2) + (b + 1) / 2) * 2^m)** Donde** b = sesgo exponente* m = número de bits de mantissa*/val.i -= 1 c) c) 23;Subtract 2^m. */val.i > 1;/* Divide por 2. */val.i += 1 c) c) 29;/* Add ((b +1) / 2) * 2^m. */Regreso val.f;/* Interpretar de nuevo como flotante */}

Las tres operaciones matemáticas que forman el núcleo de la función anterior se pueden expresar en una sola línea. Se puede agregar un ajuste adicional para reducir el error relativo máximo. Entonces, las tres operaciones, no incluyendo el yeso, pueden ser reescritas como

val.i = ()1 c) c) 29) + ()val.i " 1) - ()1 c) c) 22) + a;

donde a es un sesgo para ajustar los errores de aproximación. Por ejemplo, con a = 0 los resultados son precisos para potencias pares de 2 (por ejemplo, 1,0), pero para otros números los resultados serán ligeramente demasiado grandes (por ejemplo, 1,5 para 2,0 en lugar de 1,414... con un 6% de error). Con a = −0x4B0D2, el error relativo máximo se minimiza a ±3,5%.

Si la aproximación se utilizará para una suposición inicial para el método de Newton a la ecuación ${displaystyle (1/x^{2})-S=0}$ , entonces se prefiere la forma recíproca mostrada en la siguiente sección.

Recíproco de la raíz cuadrada

A continuación se incluye una variante de la rutina anterior, que puede utilizarse para calcular la reciproca de la raíz cuadrada, es decir, ${displaystyle x^{-1/2}}$ En cambio, fue escrito por Greg Walsh. La aproximación integer-shift produjo un error relativo de menos del 4%, y el error cayó más allá del 0,15% con una iteración del método de Newton en la línea siguiente. En los gráficos de la computadora es una manera muy eficiente de normalizar un vector.

flotador invSqrt()flotador x) {} flotador xhalf = 0,5f * x; sindicato {} flotador x; int i; } u; u.x = x; u.i = 0x5f375a86 - ()u.i " 1); /* La siguiente línea se puede repetir cualquier número de veces para aumentar la precisión */ u.x = u.x * ()1,5f - xhalf * u.x * u.x); Regreso u.x;}

Algunos hardware VLSI implementan la raíz cuadrada inversa utilizando una estimación polinómica de segundo grado seguida de una iteración de Goldschmidt.

Cuadrado negativo o complejo

Si S < 0, entonces su raíz cuadrada principal es

{displaystyle {sqrt {S}}={sqrt {vert Svert }},,i,.}

Si S = a+bi donde a y b son reales y b ≠ 0, entonces su raíz cuadrada principal es

{displaystyle {sqrt {S}}={sqrt {frac {vert Svert +a}{2}}},+,operatorname {sgn}(b){sqrt {frac {vert Svert -a}{2}}},,i,.}

Esto se puede verificar elevando la raíz al cuadrado. Aquí

{displaystyle vert Svert ={sqrt {a^{2}+b^{2}}}}

es el módulo de S. La raíz cuadrada principal de un número complejo se define como la raíz con la parte real no negativa.

Más resultados...