Método de rigidez directa

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Como uno de los métodos de análisis estructural, el método de rigidez directa, también conocido como método de rigidez matricial, es particularmente adecuado para el análisis automatizado por computadora de estructuras complejas. incluido el tipo estáticamente indeterminado. Es un método matriz que hace uso de los miembros' Relaciones de rigidez para calcular las fuerzas y desplazamientos de los miembros en estructuras. El método de rigidez directa es la implementación más común del método de elementos finitos (FEM). Al aplicar el método, el sistema debe modelarse como un conjunto de elementos idealizados más simples interconectados en los nodos. Las propiedades de rigidez del material de estos elementos se compilan luego, mediante matemáticas matriciales, en una única ecuación matricial que gobierna el comportamiento de toda la estructura idealizada. Los desplazamientos y fuerzas desconocidos de la estructura se pueden determinar resolviendo esta ecuación. El método de rigidez directa forma la base de la mayoría del software de elementos finitos comercial y gratuito.

El método de rigidez directa se originó en el campo aeroespacial. Los investigadores estudiaron diversos enfoques para el análisis de estructuras complejas de aviones. Estos incluían la teoría de la elasticidad, los principios energéticos en la mecánica estructural, el método de la flexibilidad y el método de la rigidez de la matriz. Fue a través del análisis de estos métodos que el método de rigidez directa surgió como un método eficiente idealmente adecuado para la implementación en computadora.

Historia

Entre 1934 y 1938 A. R. Collar y W. J. Duncan publicaron los primeros artículos con la representación y terminología de los sistemas matriciales que se utilizan en la actualidad. La investigación aeroelástica continuó durante la Segunda Guerra Mundial, pero las restricciones de publicación de 1938 a 1947 hicieron que este trabajo fuera difícil de rastrear. El segundo gran avance en el análisis estructural matricial se produjo entre 1954 y 1955, cuando el profesor John H. Argyris sistematizó el concepto de ensamblar componentes elementales de una estructura en un sistema de ecuaciones. Finalmente, el 6 de noviembre de 1959, M. J. Turner, jefe de la Unidad de Dinámica Estructural de Boeing, publicó un artículo en el que describía el método de rigidez directa como un modelo eficiente para la implementación informática (Felippa 2001).

Relaciones de rigidez de miembros

Una relación típica de rigidez de un miembro tiene la siguiente forma general:

{displaystyle mathbf {Q} ^{m}=mathbf {k} ^{m}mathbf {q} ^{m}+mathbf {Q} ^{om}}

()1)

dónde

m = número de miembro m.

{displaystyle mathbf {Q} ^{m}}

= vector de las fuerzas características del miembro, que son fuerzas internas desconocidas.

{displaystyle mathbf {k} ^{m}}

= matriz de rigidez miembro que caracteriza la resistencia del miembro contra las deformaciones.

{displaystyle mathbf {q} ^{m}}

= vector de los desplazamientos o deformaciones característicos del miembro.

{displaystyle mathbf {Q} ^{om}}

= vector de las fuerzas características del miembro causadas por efectos externos (como fuerzas conocidas y cambios de temperatura) aplicadas al miembro mientras

{displaystyle mathbf {q} ^{m}=0}

Si ${displaystyle mathbf {q} ^{m}}$ son deformaciones miembros en lugar de desplazamientos absolutos, entonces ${displaystyle mathbf {Q} ^{m}}$ son fuerzas miembros independientes, y en tal caso (1) puede ser invertido para ceder los llamados matriz de flexibilidad, que se utiliza en el método de flexibilidad.

Relación de rigidez del sistema

Para un sistema con muchos miembros interconectados en puntos llamados nodos, los miembros' Las relaciones de rigidez como la ecuación (1) se pueden integrar haciendo uso de las siguientes observaciones:

Deformaciones de miembros ${displaystyle mathbf {q} ^{m}}$ puede expresarse en términos de desplazamientos nodales del sistema r para garantizar la compatibilidad entre los miembros. Esto implica que r serán los primeros desconocidos.
Las fuerzas miembros ${displaystyle mathbf {Q} ^{m}}$ ayudar a mantener los nodos en equilibrio bajo las fuerzas nodal R. Esto implica que el lado derecho de (1) se integrará en el lado derecho de las siguientes ecuaciones de equilibrio nodal para todo el sistema:

{displaystyle mathbf {R} =mathbf {Kr} +mathbf {R} ^{o}}

()2)

dónde

{displaystyle mathbf {R} }

= vector de fuerzas nodales, representando fuerzas externas aplicadas a los nodos del sistema.

{displaystyle mathbf {K} }

= matriz de rigidez del sistema, que se establece por . la rigidez de los miembros

{displaystyle mathbf {k} ^{m}}

{displaystyle mathbf {r} }

= vector de los desplazamientos nodales del sistema que pueden definir todas las configuraciones deformadas posibles del sistema sujetas a fuerzas nodales arbitrarias R.

{displaystyle mathbf {R} ^{o}}

= vector de fuerzas nodales equivalentes, representando todos los efectos externos distintos de las fuerzas nodales que ya están incluidas en el vector anterior de la fuerza nodal R. Este vector está establecido por el montaje de los miembros '

{displaystyle mathbf {Q} ^{om}}

Solución

La matriz de rigidez del sistema K es cuadrado desde los vectores R y r tienen el mismo tamaño. Además, es simétrico porque ${displaystyle mathbf {k} ^{m}}$ es simétrico. Una vez que las restricciones de soporte se contabilizan en (2), los desplazamientos nodales se encuentran resolviendo el sistema de ecuaciones lineales (2), simbólicamente:

{displaystyle mathbf {r} =mathbf {K} ^{-1}(mathbf {R} -mathbf {R} ^{o})qquad qquad qquad mathrm {(3)} }

Posteriormente, las fuerzas características de los miembros pueden encontrarse en Eq.(1) donde ${displaystyle mathbf {q} ^{m}}$ se puede encontrar desde r por consideración de compatibilidad.

El método de rigidez directa

Es común tener Eq.(1) en una forma donde ${displaystyle mathbf {q} ^{m}}$ y ${displaystyle mathbf {Q} ^{om}}$ son, respectivamente, los desplazamientos y fuerzas al final de los miembros que coinciden en la dirección con r y R. En tal caso, ${displaystyle mathbf {K} }$ y ${displaystyle mathbf {R} ^{o}}$ se puede obtener mediante la supresión directa de las matrices de los miembros ${displaystyle mathbf {k} ^{m}}$ y ${displaystyle mathbf {Q} ^{om}}$ . El método es entonces conocido como el método de rigidez directa.

Las ventajas y desventajas del método de rigidez de la matriz se comparan y analizan en el artículo sobre el método de flexibilidad.

Ejemplo

Desglose

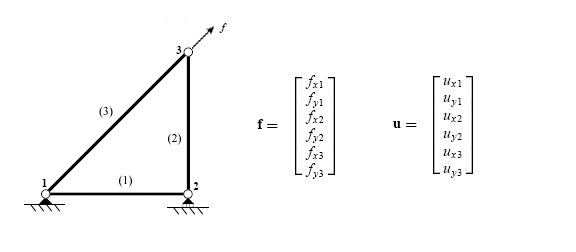
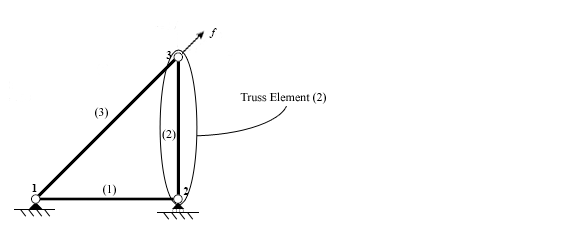
El primer paso al utilizar el método de rigidez directa es identificar los elementos individuales que componen la estructura.

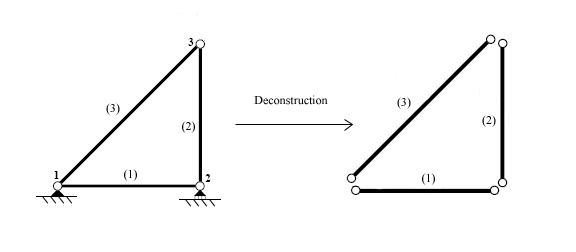
Una vez identificados los elementos, la estructura se desconecta en los nodos, los puntos que conectan los diferentes elementos entre sí.

Luego, cada elemento se analiza individualmente para desarrollar ecuaciones de rigidez de miembros. Las fuerzas y desplazamientos están relacionados a través de la matriz de rigidez del elemento que depende de la geometría y propiedades del elemento.

Un elemento de celosía sólo puede transmitir fuerzas en compresión o tensión. Esto significa que en dos dimensiones, cada nodo tiene dos grados de libertad (DOF): desplazamiento horizontal y vertical. La ecuación resultante contiene una matriz de rigidez de cuatro por cuatro.

${displaystyle {begin{bmatrix}f_{x1}\f_{y1}\f_{x2}\f_{y2}\end{bmatrix}}={begin{bmatrix}k_{11}&k_{12}&k_{13}&k_{14}\k_{21}&k_{22}&k_{23}&k_{24}\k_{31}&k_{32}&k_{33}&k_{34}\k_{41}&k_{42}&k_{43}&k_{44}\end{bmatrix}}{begin{bmatrix}u_{x1}\u_{y1}\u_{x2}\u_{y2}\end{bmatrix}}}$

Un elemento de marco es capaz de soportar momentos de flexión además de compresión y tensión. Esto da como resultado tres grados de libertad: desplazamiento horizontal, desplazamiento vertical y rotación en el plano. La matriz de rigidez en este caso es de seis por seis.

${displaystyle {begin{bmatrix}f_{x1}\f_{y1}\m_{z1}\f_{x2}\f_{y2}\m_{z2}\end{bmatrix}}={begin{bmatrix}k_{11}&k_{12}&k_{13}&k_{14}&k_{15}&k_{16}\k_{21}&k_{22}&k_{23}&k_{24}&k_{25}&k_{26}\k_{31}&k_{32}&k_{33}&k_{34}&k_{35}&k_{36}\k_{41}&k_{42}&k_{43}&k_{44}&k_{45}&k_{46}\k_{51}&k_{52}&k_{53}&k_{54}&k_{55}&k_{56}\k_{61}&k_{62}&k_{63}&k_{64}&k_{65}&k_{66}\end{bmatrix}}{begin{bmatrix}u_{x1}\u_{y1}\theta _{z1}\u_{x2}\u_{y2}\theta _{z2}\end{bmatrix}}}$

También se pueden incorporar otros elementos, como placas y carcasas, al método de rigidez directa y se deben desarrollar ecuaciones similares.

Asamblea

Una vez que se han desarrollado las relaciones de rigidez de los elementos individuales, se deben ensamblar en la estructura original. El primer paso en este proceso es convertir las relaciones de rigidez de los elementos individuales en un sistema global para toda la estructura. En el caso de un elemento de celosía, la forma global del método de rigidez depende del ángulo del elemento con respecto al sistema de coordenadas global (este sistema suele ser el sistema de coordenadas cartesiano tradicional).

${displaystyle {begin{bmatrix}f_{x1}\f_{y1}\f_{x2}\f_{y2}\end{bmatrix}}={frac {EA}{L}}{begin{bmatrix}c^{2}&sc&-c^{2}&-sc\sc&s^{2}&-sc&-s^{2}\-c^{2}&-sc&c^{2}&sc\-sc&-s^{2}&sc&s^{2}\end{bmatrix}}{begin{bmatrix}u_{x1}\u_{y1}\u_{x2}\u_{y2}\end{bmatrix}}{begin{array}{r }s=sin beta \c=cos beta \end{array}}}$ (para un elemento de tress en ángulo β)Equivalentemente, ${displaystyle {begin{bmatrix}f_{x1}\f_{y1}\hline f_{x2}\f_{y2}end{bmatrix}}={frac {EA}{L}}left[{begin{array}{c c|c c}c_{x}c_{x}&c_{x}c_{y}&-c_{x}c_{x}&-c_{x}c_{y}\c_{y}c_{x}&c_{y}c_{y}&-c_{y}c_{x}&-c_{y}c_{y}\hline -c_{x}c_{x}&-c_{x}c_{y}&c_{x}c_{x}&c_{x}c_{y}\-c_{y}c_{x}&-c_{y}c_{y}&c_{y}c_{x}&c_{y}c_{y}\end{array}}right]{begin{bmatrix}u_{x1}\u_{y1}\hline u_{x2}\u_{y2}end{bmatrix}}}$

Donde ${displaystyle c_{x}}$ y ${displaystyle c_{y}}$ son la dirección cosines del elemento de tress (es decir, son componentes de un vector unitario alineado con el miembro). Esta forma revela cómo generalizar la rigidez del elemento a las trusas espaciales 3-D simplemente extendiendo el patrón que es evidente en esta formulación.

Después de desarrollar la matriz de rigidez del elemento en el sistema de coordenadas global, se deben fusionar en una única matriz de rigidez "maestra" o "global". Al fusionar estas matrices, se deben seguir dos reglas: compatibilidad de desplazamientos y equilibrio de fuerzas en cada nodo. Estas reglas se mantienen al relacionar los desplazamientos nodales de los elementos con los desplazamientos nodales globales.

Los vectores de fuerza y desplazamiento global contienen cada uno una entrada para cada grado de libertad en la estructura. Las matrices de rigidez de los elementos se fusionan aumentando o expandiendo cada matriz en conformación con los vectores de carga y desplazamiento global.

${displaystyle k^{(1)}={frac {EA}{L}}{begin{bmatrix}1&0&-1&0\0&0&0&0\-1&0&1&0\0&0&0&0\end{bmatrix}}rightarrow K^{(1)}={frac {EA}{L}}{begin{bmatrix}1&0&-1&0&0&0\0&0&0&0&0&0\-1&0&1&0&0&0\0&0&0&0&0&0\0&0&0&0&0&0\0&0&0&0&0&0\end{bmatrix}}}$ (para el elemento 1) de la estructura anterior)

Finalmente, la matriz de rigidez global se construye sumando las matrices de elementos expandidos individuales.

Solución

Una vez construidos la matriz de rigidez global, el vector de desplazamiento y el vector de fuerza, el sistema se puede expresar como una ecuación matricial única.

Para cada grado de libertad en la estructura, se conoce el desplazamiento o la fuerza.

Después de insertar el valor conocido para cada grado de libertad, la ecuación de rigidez maestra está completa y lista para ser evaluada. Hay varios métodos diferentes disponibles para evaluar una ecuación de matriz incluyendo pero no limitado a la descomposición de Cholesky y la evaluación de fuerza bruta de sistemas de ecuaciones. Si una estructura no está adecuadamente restringida, la aplicación de una fuerza hará que se mueva rígidamente y se deben añadir condiciones de apoyo adicionales.

El método descrito en esta sección pretende ser una descripción general del método de rigidez directa. Se deben consultar fuentes adicionales para obtener más detalles sobre el proceso, así como las suposiciones sobre las propiedades del material inherentes al proceso.

Aplicaciones

El método de rigidez directo fue desarrollado específicamente para implementarse de manera efectiva y sencilla en software de computadora para evaluar estructuras complicadas que contienen una gran cantidad de elementos. Hoy en día, casi todos los solucionadores de elementos finitos disponibles se basan en el método de rigidez directa. Si bien cada programa utiliza el mismo proceso, muchos se han simplificado para reducir el tiempo de cálculo y la memoria requerida. Para lograr esto, se han desarrollado atajos.

Una de las áreas más importantes para utilizar el método de rigidez directa es el campo del análisis estructural, donde este método se ha incorporado al software de modelado. El software permite a los usuarios modelar una estructura y, después de que el usuario define las propiedades materiales de los elementos, el programa genera automáticamente relaciones entre elementos y rigidez global. Cuando se aplican varias condiciones de carga, el software evalúa la estructura y genera las deflexiones para el usuario.

Más resultados...