Metaheurística

En informática y optimización matemática, una metaheurística es un procedimiento o heurística de nivel superior diseñado para encontrar, generar, ajustar o seleccionar una heurística (algoritmo de búsqueda parcial) que pueda proporcionar una respuesta suficientemente buena. solución a un problema de optimización o un problema de aprendizaje automático, especialmente con información incompleta o imperfecta o capacidad de cálculo limitada. Las metaheurísticas muestrean un subconjunto de soluciones que, de otro modo, sería demasiado grande para enumerarlo o explorarlo por completo. Las metaheurísticas pueden hacer relativamente pocas suposiciones sobre el problema de optimización que se resuelve y, por lo tanto, pueden usarse para una variedad de problemas.

En comparación con los algoritmos de optimización y los métodos iterativos, las metaheurísticas no garantizan que se pueda encontrar una solución globalmente óptima para algún tipo de problema. Muchas metaheurísticas implementan alguna forma de optimización estocástica, de modo que la solución encontrada depende del conjunto de variables aleatorias generadas. En la optimización combinatoria, al buscar en un gran conjunto de soluciones factibles, las metaheurísticas a menudo pueden encontrar buenas soluciones con menos esfuerzo computacional que los algoritmos de optimización, los métodos iterativos o las heurísticas simples. Como tales, son enfoques útiles para problemas de optimización. Se han publicado varios libros y artículos de investigación sobre el tema. Una revisión de la literatura sobre optimización metaheurística sugirió que fue Fred Glover quien acuñó la palabra metaheurística.

La mayor parte de la literatura sobre metaheurísticas es de naturaleza experimental y describe resultados empíricos basados en experimentos informáticos con los algoritmos. Pero también están disponibles algunos resultados teóricos formales, a menudo sobre la convergencia y la posibilidad de encontrar el óptimo global. Se han publicado muchos métodos metaheurísticos con afirmaciones de novedad y eficacia práctica. Si bien el campo también presenta investigaciones de alta calidad, muchas de las publicaciones han sido de mala calidad; Los defectos incluyen vaguedad, falta de elaboración conceptual, experimentos deficientes e ignorancia de la literatura previa.

Propiedades

Estas son propiedades que caracterizan a la mayoría de las metaheurísticas:

• Las metaheurísticas son estrategias que guían el proceso de búsqueda.
• El objetivo es explorar eficientemente el espacio de búsqueda para encontrar soluciones casi óptimas.
• Las técnicas que constituyen algoritmos metaheurísticos van desde procedimientos simples de búsqueda local a procesos complejos de aprendizaje.
• Los algoritmos metaheurísticos son aproximados y generalmente no-deterministas.
• Las metaheurísticas no son específicas para problemas.

Clasificación

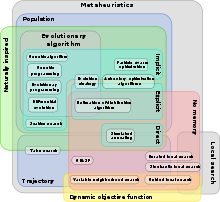
Existe una amplia variedad de metaheurísticas y una serie de propiedades con respecto a las cuales clasificarlas.

Búsqueda local frente a búsqueda global

Un enfoque consiste en caracterizar el tipo de estrategia de búsqueda. Un tipo de estrategia de búsqueda es una mejora de los algoritmos de búsqueda locales simples. Un algoritmo de búsqueda local muy conocido es el método de escalada que se utiliza para encontrar óptimos locales. Sin embargo, escalar colinas no garantiza encontrar soluciones óptimas globales.

Se propusieron muchas ideas metaheurísticas para mejorar la heurística de búsqueda local con el fin de encontrar mejores soluciones. Dichas metaheurísticas incluyen recocido simulado, búsqueda tabú, búsqueda local iterada, búsqueda de vecindad variable y GRASP. Estas metaheurísticas pueden clasificarse como metaheurísticas de búsqueda local o de búsqueda global.

Otras metaheurísticas de búsqueda global que no se basan en búsquedas locales suelen ser metaheurísticas basadas en la población. Dichas metaheurísticas incluyen optimización de colonias de hormigas, cálculo evolutivo como algoritmo genético o estrategias de evolución, optimización de enjambre de partículas, algoritmo de optimización de jinetes y algoritmo de búsqueda de alimento bacteriano.

Solución única frente a basada en la población

Otra dimensión de la clasificación es la búsqueda de solución única versus búsquedas basadas en la población. Los enfoques de solución única se centran en modificar y mejorar una única solución candidata; Las metaheurísticas de solución única incluyen recocido simulado, búsqueda local iterada, búsqueda de vecindad variable y búsqueda local guiada. Los enfoques basados en la población mantienen y mejoran múltiples soluciones candidatas, a menudo utilizando características de la población para guiar la búsqueda; Las metaheurísticas basadas en poblaciones incluyen computación evolutiva y optimización de enjambres de partículas. Otra categoría de metaheurística es la inteligencia de enjambre, que es un comportamiento colectivo de agentes descentralizados y autoorganizados en una población o enjambre. La optimización de colonias de hormigas, la optimización de enjambres de partículas, la optimización cognitiva social y el algoritmo de búsqueda de alimento bacteriano son ejemplos de esta categoría.

Algoritmos de hibridación y meméticos

Una metaheurística híbrida es aquella que combina una metaheurística con otros enfoques de optimización, como algoritmos de programación matemática, programación de restricciones y aprendizaje automático. Ambos componentes de una metaheurística híbrida pueden ejecutarse simultáneamente e intercambiar información para guiar la búsqueda.

Por otro lado, los algoritmos meméticos representan la sinergia de un enfoque evolutivo o basado en la población con aprendizaje individual separado o procedimientos de mejora local para la búsqueda de problemas. Un ejemplo de algoritmo memético es el uso de un algoritmo de búsqueda local en lugar o además de un operador de mutación básico en algoritmos evolutivos.

Metaheurísticas paralelas

Una metaheurística paralela es aquella que utiliza las técnicas de programación paralela para ejecutar múltiples búsquedas metaheurísticas en paralelo; estos pueden variar desde esquemas distribuidos simples hasta ejecuciones de búsqueda simultáneas que interactúan para mejorar la solución general.

Metaheurísticas inspiradas en la naturaleza y basadas en metáforas

Un área de investigación muy activa es el diseño de metaheurísticas inspiradas en la naturaleza. Muchas metaheurísticas recientes, especialmente los algoritmos basados en computación evolutiva, están inspirados en sistemas naturales. La naturaleza actúa como fuente de conceptos, mecanismos y principios para el diseño de sistemas informáticos artificiales para abordar problemas computacionales complejos. Dichas metaheurísticas incluyen recocido simulado, algoritmos evolutivos, optimización de colonias de hormigas y optimización de enjambres de partículas. Un gran número de metaheurísticas más recientes inspiradas en metáforas han comenzado a atraer críticas en la comunidad investigadora por ocultar su falta de novedad detrás de una metáfora elaborada.

Aplicaciones

Las metaheurísticas se utilizan para todo tipo de problemas de optimización, desde problemas continuos hasta problemas de enteros mixtos hasta optimización combinatoria o combinaciones de los mismos. En la optimización combinatoria, se busca una solución óptima en un espacio de búsqueda discreto. Un problema de ejemplo es el problema del viajante, donde el espacio de búsqueda de soluciones candidatas crece más rápido que exponencialmente a medida que aumenta el tamaño del problema, lo que hace que una búsqueda exhaustiva de la solución óptima sea inviable. Además, los problemas combinatorios multidimensionales, incluida la mayoría de los problemas de diseño en ingeniería, como la búsqueda de formas y la búsqueda de comportamientos, sufren la maldición de la dimensionalidad, lo que también los hace inviables para métodos analíticos o de búsqueda exhaustiva.

Las metaheurísticas también se aplican con frecuencia a problemas de programación. Un representante típico de esta clase de tareas combinatorias es la programación del taller, que implica asignar los pasos de trabajo de los trabajos a las estaciones de procesamiento de tal manera que todos los trabajos se completen a tiempo y en el menor tiempo posible. En la práctica, a menudo es necesario observar restricciones, p. limitando la secuencia permitida de los pasos de trabajo de un trabajo mediante flujos de trabajo predefinidos y/o en relación con la utilización de recursos, p. en forma de suavización de la demanda de energía. Las metaheurísticas populares para problemas combinatorios incluyen los algoritmos genéticos de Holland et al., la búsqueda de dispersión y la búsqueda tabú de Glover.

Otro gran campo de aplicación son las tareas de optimización en espacios de búsqueda continuos o de enteros mixtos. Esto incluye, por ejemplo, la optimización del diseño o diversas tareas de ingeniería. Un ejemplo de la combinación de optimización combinatoria y continua es la planificación de trayectorias de movimiento favorables para robots industriales.

Marcos de optimización metaheurística

Un MOF se puede definir como ''un conjunto de herramientas de software que proporcionan una implementación correcta y reutilizable de un conjunto de metaheurísticas, y los mecanismos básicos para acelerar la implementación de las heurísticas subordinadas de su socio (posiblemente incluyendo codificaciones de solución y técnicas). operadores específicos), que son necesarios para resolver un caso de problema particular utilizando las técnicas proporcionadas''.

Hay muchas herramientas de optimización candidatas que pueden considerarse como un MOF de diferentes características: Comet, EvA2, evolvica, Evolutionary::Algorithm, GAPlayground, jaga, JCLEC, JGAP, jMetal, n-genes, Open Beagle, Opt4j, ParadisEO/EO, Pisa, Watchmaker, FOM, Hypercube, HotFrame, Templar, EasyLocal, iOpt, OptQuest, JDEAL, Optimization Algorithm Toolkit, HeuristicLab, MAFRA, Localizer, GALIB, DREAM, Discropt, MALLBA, MAGMA, Metaheuristics.jl, UOF y OptaPlanner.

Contribuciones

Existen muchas metaheurísticas diferentes y continuamente se proponen nuevas variantes. Algunas de las contribuciones más significativas al campo son:

• 1952: Robbins y Monro trabajan en métodos de optimización estocástica.
• 1954: Barricelli realiza las primeras simulaciones del proceso de evolución y las utiliza en problemas generales de optimización.
• 1963: Rastrigin propone búsqueda aleatoria.
• 1965: Matyas propone optimización aleatoria.
• 1965: Nelder y Mead proponen una heurística simple, que fue mostrada por Powell para converger a puntos no estacionarios sobre algunos problemas.
• 1965: Ingo Rechenberg descubre el primer algoritmo de Evolution Strategies.
• 1966: Fogel et al. proponer programación evolutiva.
• 1970: Hastings propone el algoritmo de Metropolis-Hastings.
• 1970: Cavicchio propone la adaptación de parámetros de control para un optimizador.
• 1970: Kernighan y Lin proponen un método de partición de gráficos, relacionado con búsqueda de profundidad variable y búsqueda basada en la prohibición (tabu).
• 1975: Holanda propone el algoritmo genético.
• 1977: Glover propone búsqueda de dispersión.
• 1978: Mercer y Sampson proponen un metaplan para ajustar los parámetros de un optimizador utilizando otro optimizador.
• 1980: Smith describe la programación genética.
• 1983: Kirkpatrick et al. proponen amasamiento simulado.
• 1986: Glover propone la búsqueda tabu, primera mención del término metaheurística.
• 1989: Moscato propone algoritmos meméticos.
• 1990: Moscato y Fontanari, y Dueck y Scheuer, propusieron de forma independiente una regla de actualización determinista para el aniquilamiento simulado que aceleró la búsqueda. Esto llevó al umbral aceptando metaheurística.
• 1992: Dorigo introduce la optimización de la colonia de hormigas en su tesis doctoral.
• 1995: Wolpert y Macready prueban que no hay teoremas de almuerzo gratis.